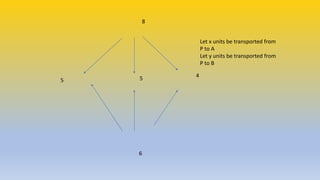
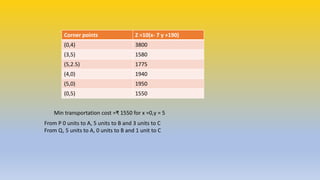
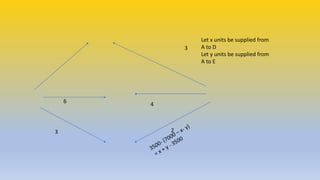
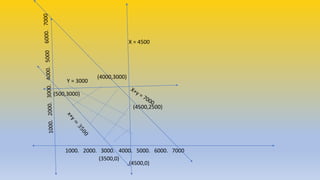
The document discusses transportation problems in linear programming, demonstrating how to minimize transportation costs with specific examples. It presents scenarios involving factories supplying depots and the calculations necessary to determine optimal transport routes and quantities. Detailed graphs and cost equations are provided to illustrate the problem-solving process.

1. TRANSPORTATION PROBLEMS
GRADE 12 MATH
COLLEGE MATH

2. PREVIEW:
THIS VIDEO ILLUSTRATES TRANSPORTATION PROBLEMS (A PART OF
LINEAR PROGRAMMING) AND HOW THEY ARE SOLVED.
PROBLEMS ARE EXPLAINED IN DETAIL THROUGH DIAGRAMS AND
GRAPHS.
SO WELCOME TO THE WORLD OF LINEAR PROGRAMMING!

3. Question 1
A company has 2 factories located at P and Q and has 3 depots at A, B and C. The weekly
requirement of A, B and C is 5,5 and 4 units respectively while the production capacities of
P and Q are 8 and 6 units respectively. The cost in Rupees of transportation per unit is given
Cost
TO/FROM A B C
P 160 100 150
Q 100 120 100
How many units should be transported from each factory to each depot so that
Transportation cost is minimum

4. 8
6
5 5 4
Let x units be transported from
P to A
Let y units be transported from
P to B

5. Transportation cost =160x + 100y + 150( 8- x – y)+ 100 ( 5- x) +120 (5- y) + 100 ( x + y -4) +
10( x – 7y + 190)
Min z = 10( x- 7y +190)subject to

6. .

7. Corner points Z =10(x- 7 y +190)
(0,4) 3800
(3,5) 1580
(5,2.5) 1775
(4,0) 1940
(5,0) 1950
(0,5) 1550
Min transportation cost =₹ 1550 for x =0,y = 5
From P 0 units to A, 5 units to B and 3 units to C
From Q, 5 units to A, 0 units to B and 1 unit to C

8. Question 2
A company has 2 depots A and B with capacities of 7000 liitres and 4000 litres respectively. The company is
to supply oil to 3 petrol bunks D, E and F whose requirements are 4500 litres , 3000 litres and 3500 litres
respectively. The distance in km between the depots and petrol bunks is given in the following table.
Distance in km
To/from A B
D 7 3
E 6 4
F 3 2
Assume that the cost is ₹1 per litre how should the delivery be scheduled so that the cost is minimum.
What is the minimum cost

9. 6
3
3
4
2
Let x units be supplied from
A to D
Let y units be supplied from
A to E

10. Min z =7x + 6 y+ 21 00 – 3x – 3 y + 13500 – 3 x +12000 – 4 y + 2x + 2 y- 7000
Min z =3 x + y + 39500. Subject to

11. 1000. 2000. 3000. 4000. 5000. 6000. 7000
X = 4500
Y = 3000
(4500,0)
(3500,0)
(500,3000)
(4500,2500)
(4000,3000)

12. Corner points Z= 3x + y + 39500
(4500,0) 53000
(3500,0) 50000
(500,3000) 44000
(4500,2500) 55500
(4000,3000) 54500
Min transportation cost = 44000 for x = 500, y = 3000
A supplies 500 units to D, 3000 units to E and 3500 units to F
B supplies 4000 units to D, 0 units to E and 0 units to F

13. For more videos , subscribe to my channel