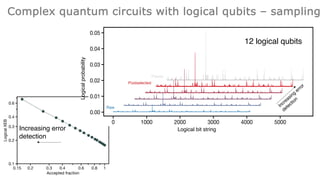
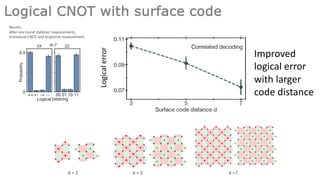
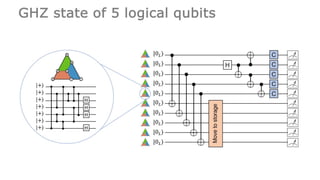
This document summarizes research on using neutral atoms for quantum computing. It describes how individual atoms can be deterministically trapped and arranged using optical tweezers and feedback. Quantum gates between atoms are performed using Rydberg interactions. High fidelity single and two-qubit gates have been achieved. Logical qubits are implemented using error correction codes like surface codes to protect against errors. Circuits with many logical qubits have been demonstrated, including GHZ states of 5 logical qubits and sampling circuits with 12 logical qubits. The goal is to scale up to thousands of physical qubits and hundreds of high-fidelity logical qubits for running quantum algorithms.

1. Towards error-corrected quantum computing
with neutral atoms
Massachusetts Institute
of Technology
MIT-Harvard Center for Ultracold
Atoms
Mikhail Lukin and Markus Greiner (Harvard)
Vladan Vuletić (MIT)

2. Outline
Basics of neutral-atom quantum computing
• Trapping and transporting atomic qubits
• Quantum gates through Rydberg interactions
• Physical-qubit gate fidelities
Logical qubits
• Surface-code qubit
• GHZ entangled state of logical qubits with error
detection
• First circuits with many logical qubits

3. A quantum computing device with atoms …
Richard Feynman

4. Controlling individual atoms

5. Trapping a single atom in a strongly focused
laser beam (optical tweezer)
N. Schlosser, G. Reymond, I. Protsenko, P. Grangier, Nature 411, 1024 (2001)

6. Trapping single atoms
• Single neutral atoms can be trapped and imaged in focused laser
beams
N. Schlosser, G. Reymond, I. Protsenko, P. Grangier, Nature 411, 1024 (2001).
1 atom
0 atoms

7. Trapping many single atoms
• Problem: probability to trap a single atom is only 50-60%
• The probability to trap N atoms simultaneously in N traps is
exponentially small
• Solution: observation and real-time feedback

8. Trapping many single atoms
deterministically
Problem: each trap is only loaded with ~50% probability.
Solution: real-time rearrangement after imaging (feedback)
M. Endres, H. Bernien, A. Keesling, H. Levine, E. Anschuetz, A. Krajenbrink, C.
Senko, V. Vuletić, M. Greiner, and M.D. Lukin, Science 354, 1024-1027 (2016).

9. Individual atoms in reconfigurable
traps
Greiner – Lukin – Vuletic collaboration
• Use atom detection and feedback (trap rearrangement) to
deterministically fill large number of traps with exactly one
atom
• Fast deterministic preparation of N atoms in chain.
M. Endres, H. Bernien, A. Keesling, H. Levine, E. Anschuetz, A. Krajenbrink, C.
Senko, V. Vuletić, M. Greiner, and M.D. Lukin, Science 354, 1024-1027 (2016).

10. Sorting 300 atoms in two dimensions
Initial loading: After sorting:
> 98% filling fraction

11. Three dimensional arrays also possible
Synthetic three-dimensional atomic structures assembled atom by atom. D. Barredo, V.
Lienhard, S. de Léséleuc, T. Lahaye & A. Browaeys, Nature 561, 79–82 (2018).

12. Quantum gates through Rydberg
interactions
• Atom can be addressed to create effective spin ½ system (qubit)
• We can trap and image individual atoms with optically resolvable
separation (few µm).
• Quantum gates require interactions.
• Can we make atoms interact over those optically resolvable
distances?
• Rydberg blockade:
D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté, and M. D. Lukin, Phys.
Rev. Lett. 85, 2208 (2000).

13. Rydberg states
Very highly excited hydrogen-like states
Extremely large size, dipole moment, polarizability
Strong Rydberg-Rydberg interactions V(R)=C6/R6
~100 MHz interaction strength over
optically resolvable 5 µm distance
Rydberg-Rydberg interactions can be used to implement
strong spin-spin interactions (or quantum gates) over optically
resolvable distances
10 µm

14. Rydberg interactions
|sñ
|rñ
Blockade radius rb~10 µm
|sñ
|rñ
Blockade radius rb
Ground
state
Rydberg
state

15. Rydberg interactions: only one atom can be excited
|sñ
|rñ
Blockade radius rbBlockade radius rb
Rydberg
interaction
|rñ
|sñ

16. Only one atom can be excited: Bell state
|sñ
|rñ
Blockade radius rbBlockade radius rb
Rydberg
interaction |rñ
|sñ

17. Quera Computing (Boston-based startup)
256-atom
machine
available for
access via
AWS 10/2022

18. Digital quantum machines

19. Error correction
• Encode the same information “logical bit” in
several copies (“physical bits”);
• Take a majority vote and reset any minority
bits that have flipped
• Problem for quantum bits: You are not allowed
to look at the qubits (i.e. quantum state must
remain unobserved)

20. Quantum error correction
• It is possible to compare the state of two or several
qubits without ever revealing the state
Z
Z Z
X
X
X
Z
Z
Z
Z
X
X
X
X
X
X
X
Z
Z Z
X
X
X
X
Z
Z
Z
Z
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z Z
Z
Z
Z
Z
X
X
X
X Z
Z Z
X
X
X
X
Z
Z
Z
Z
X
X
X
X
X
X
X
X
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Computation qubit
Ancilla (error syndrome) qubit
High threshold for errors: 1%
Logical error (pphys/pth)d/2
d

21. Digital operation of Rydberg
arrays: quantum gates
• H. Levine, A. Keesling, A. Omran, H. Bernien, S. Schwartz, A.S. Zibrov, M. Endres,
M. Greiner, V. Vuletić, and M.D. Lukin, Phys. Rev. Lett. 121, 123603 (2018).
• H. Levine, A. Keesling, G. Semeghini, A. Omran, T. T. Wang, S. Ebadi, H. Bernien,
M. Greiner, V. Vuletić, H. Pichler, and M. D. Lukin, Phys. Rev. Lett. 123, 170503
(2019).
• S. Evered, D. Bluvstein, M. Kalinowski, S. Ebadi, T. Manowitz, H. Zhou, S.H. Li,
A.A. Geim, T. T. Wang, N. Maskara, H. Levine, G. Semeghini, M. Greiner, V.
Vuletić, and M.D. Lukin, arXiv:2304.05420

22. Characterization of single-qubit gate
Single qubit fidelity
(many copies)
>0.9998
Dispersive optical systems for scalable Raman driving of hyperfine qubits. H.
Levine, D. Bluvstein, A. Keesling, T. T. Wang, S. Ebadi, G. Semeghini, A. Omran,
M. Greiner, V. Vuletić, and M.D. Lukin, Phys. Rev. A 105, 032618 (2022);

23. Two-qubit gates
Parallel two-
qubit gates on
10 pairs of
atoms

24. Two-qubit gate fidelity
Parallel two-qubit gates on 30
pairs of atoms.
Randomized benchmarking.
99.5% gate fidelity
Error below 1% threshold of
surface code.

25. Transporting entanglement
No deterioration in
entanglement
observed for
transported Bell pair

26. Logical qubits
Logical quantum processor based on reconfigurable atom arrays.
D. Bluvstein, S.J. Evered, A.A. Geim, S.H. Li, H. Zhou, T. Manovitz, S.
Ebadi, M. Cain, M. Kalinowski, D. Hangleiter, J.P. Bonilla Ataides, N.
Maskara, I. Cong, X. Gao, P. Sales Rodriguez, T. Karolyshyn, G. Semeghini,
M.J. Gullans, M. Greiner, V. Vuletić, and M.D. Lukin, Nature (in print, 2023).

27. Implementation of Toric code
Rydberg quantum gate
Syndrome qubits
are moving
Memory qubits are stationary

28. Vision for quantum processor

29. Zone layout for
logical qubit
processing

30. Logical CNOT with surface code
d = 3 d = 5 d =7
Results:
After one round stabilizer measurements,
transversal CNOT, and projective measurement
Improved
logical error
with larger
code distance
Logical
error

31. GHZ state of 5 logical qubits

32. Storage zone
Entangling zone
Logical GHZ states with Steane code

33. Classically hard sampling circuits
with logical qubits: [[8,3,2]] hypercube
code
12 logical
qubits

34. Complex quantum circuits with logical qubits – sampling
Increasing error
detection
Logical bit string
Logical
probability
Increasing
error
detection
Raw
Postselected
Theory
12 logical qubits

35. Summary and Outlook
• We are entering the era of first algorithms with logical
qubits
• Path towards large quantum simulators:
– ~1000 physical qubits achieved, 48 logical qubits
– 10,000-100,000 physical qubits within reach in next
1-2 years.
– Digital quantum simulators will be useful for science.
– Quantum error corrections seems feasible: 100 logical
qubits with error < 10-6 - 10-8 within next two years.
– What are the useful algorithms?