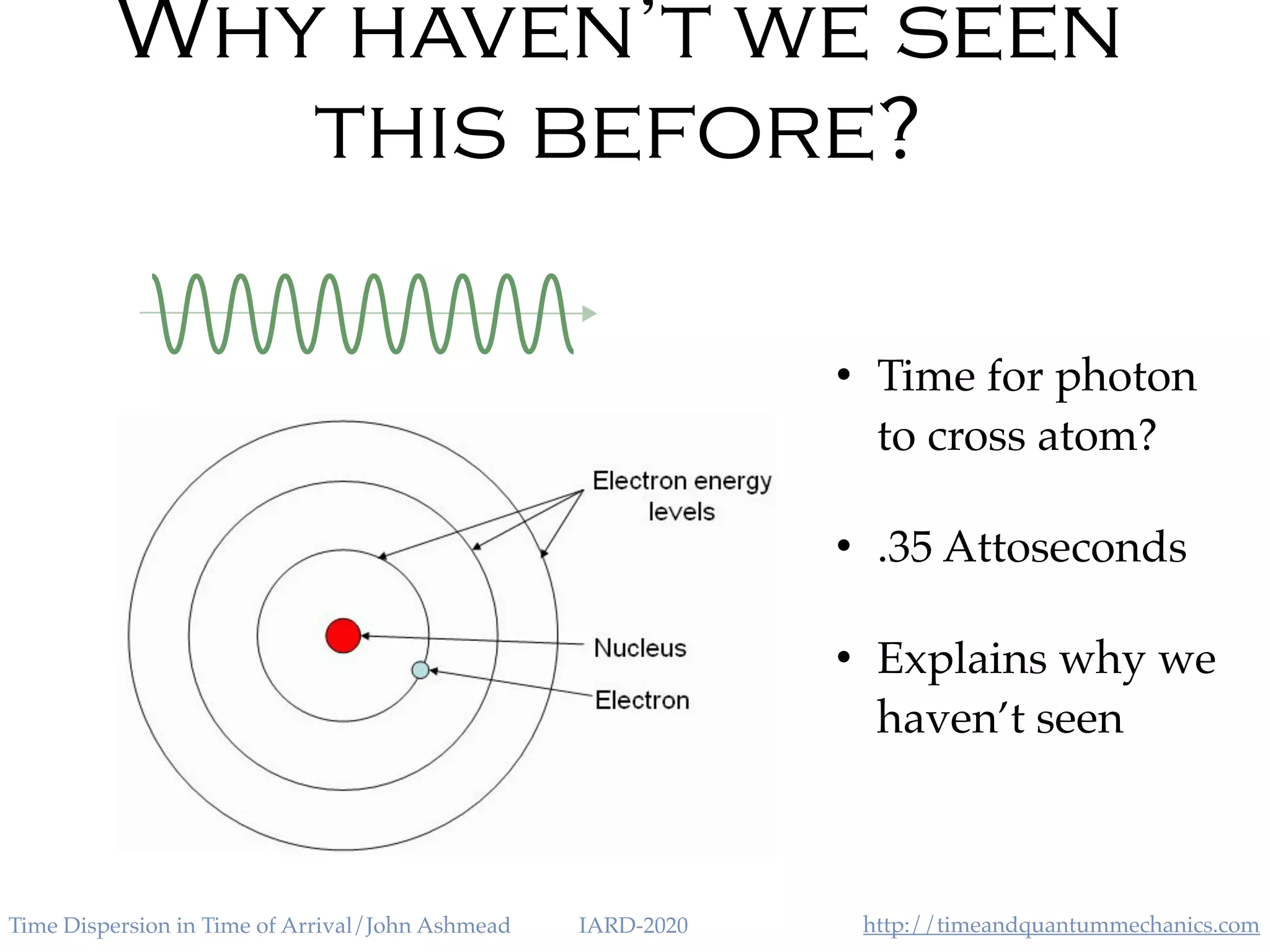
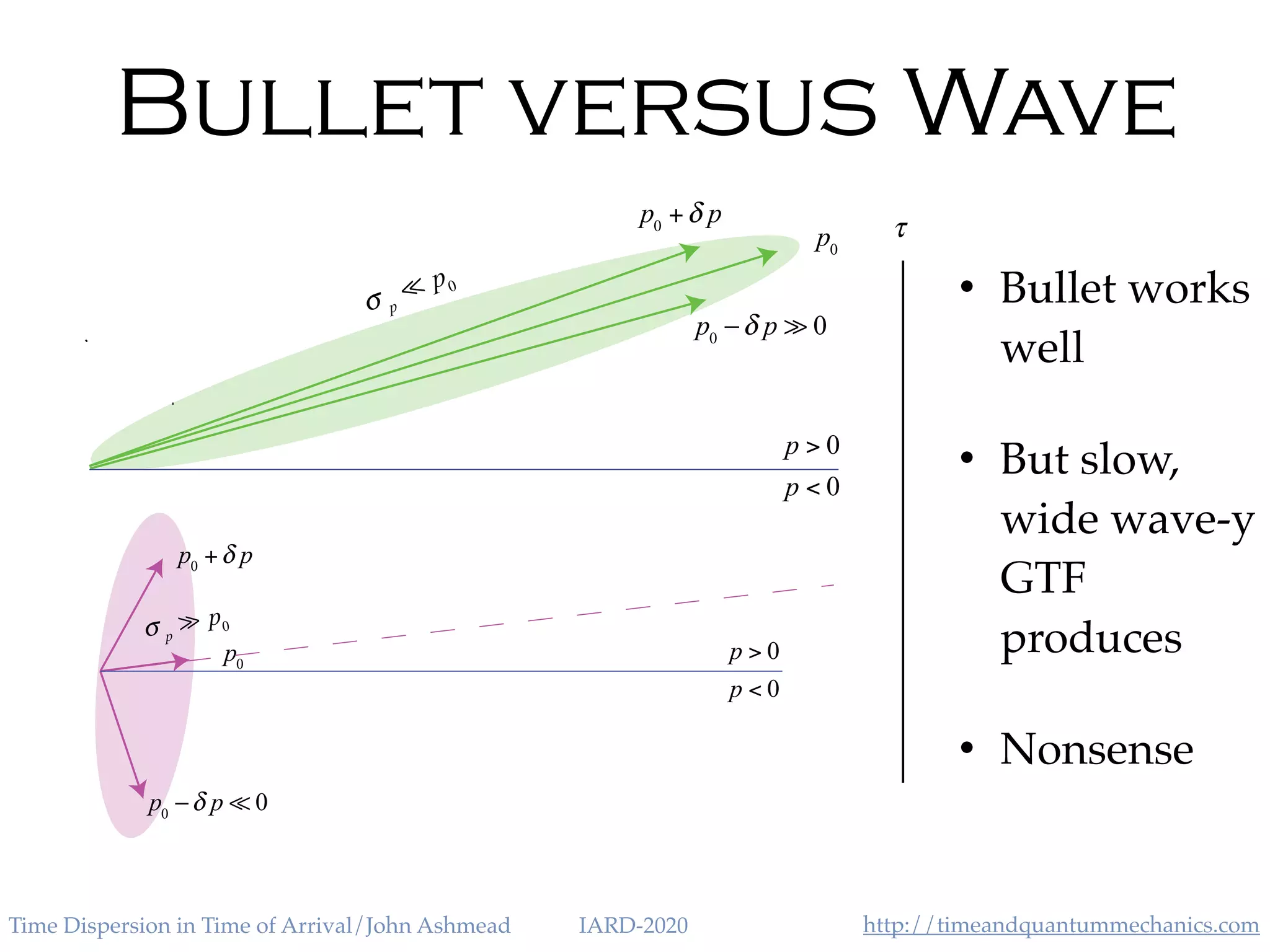
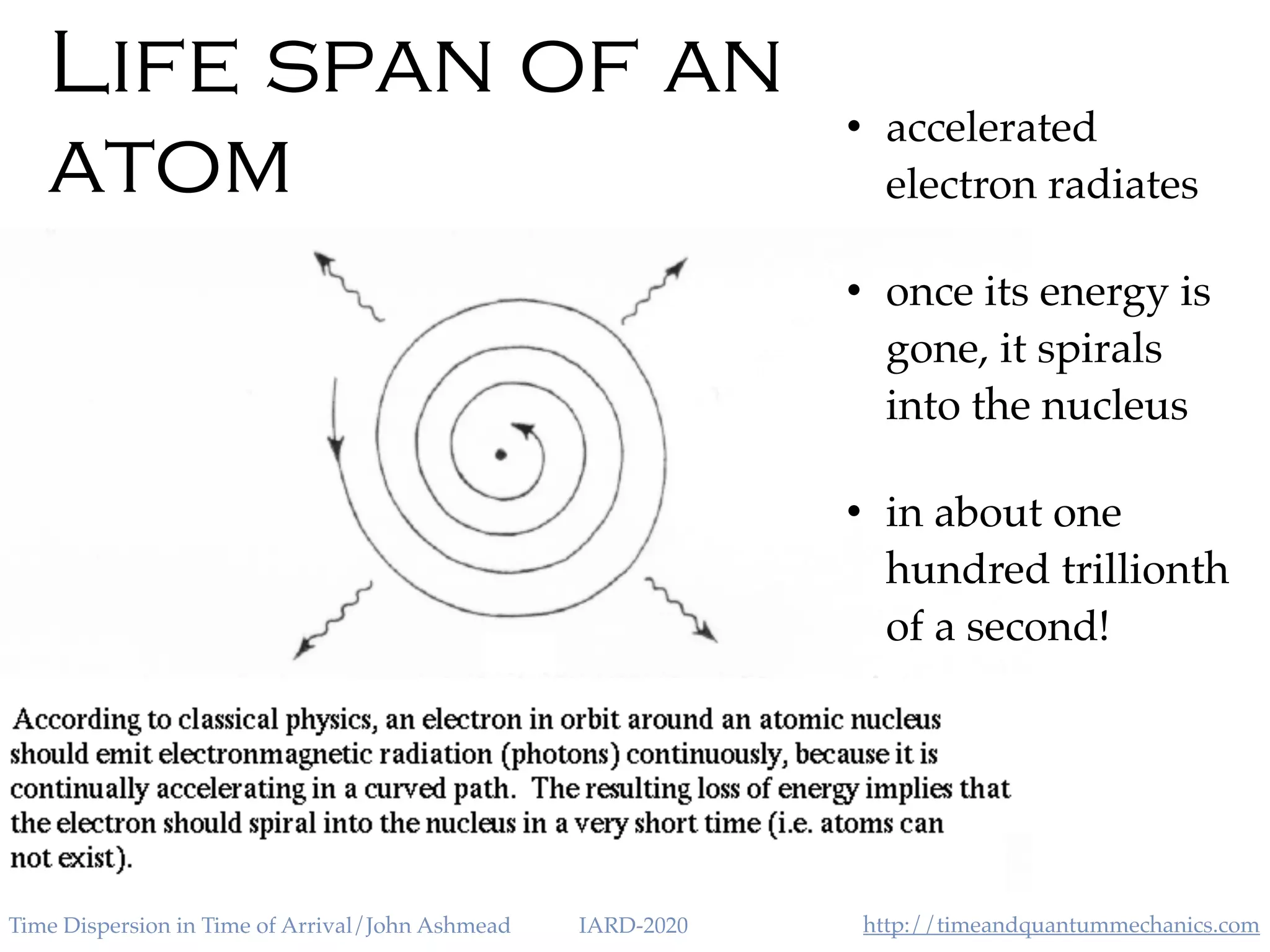
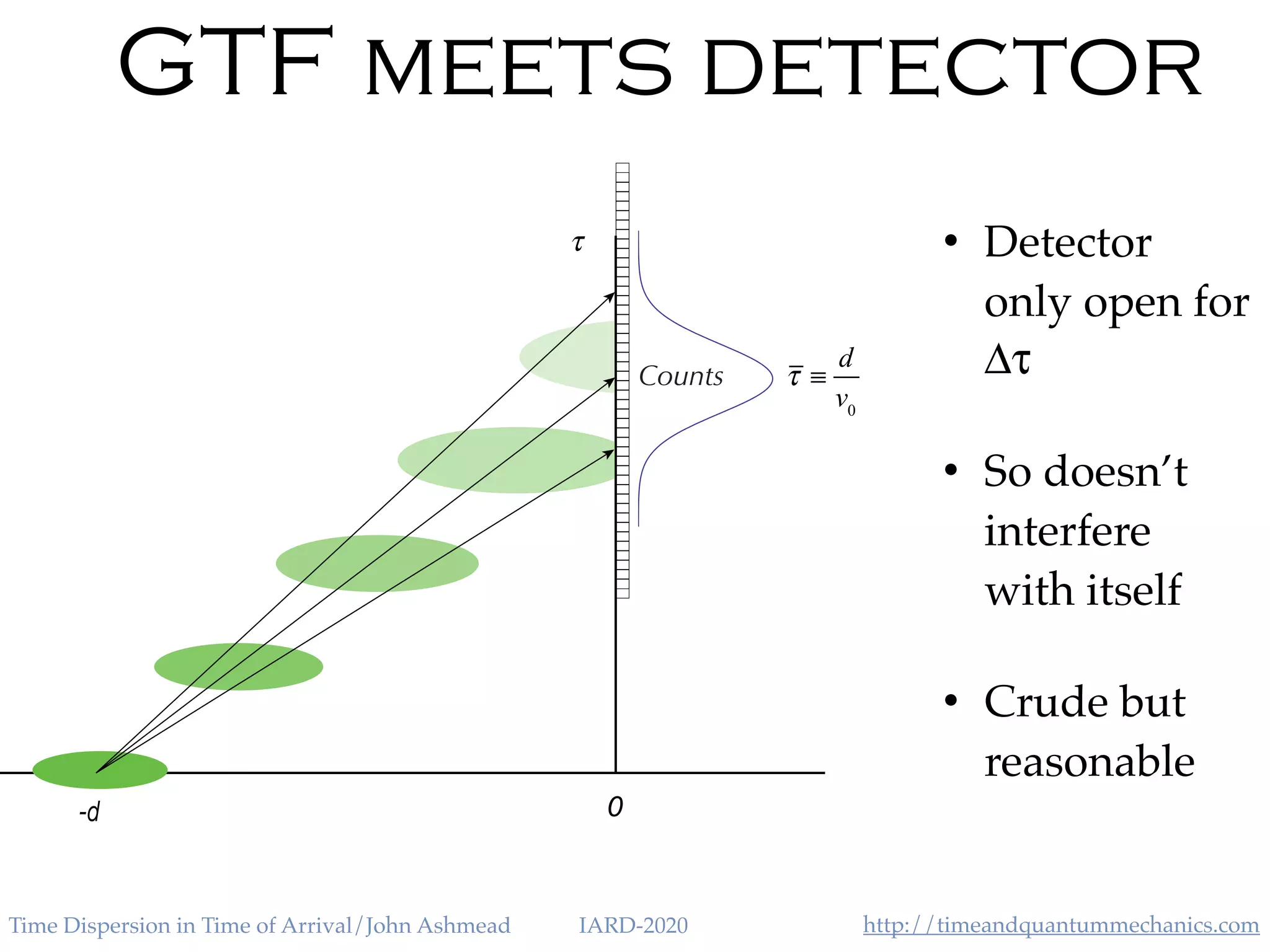
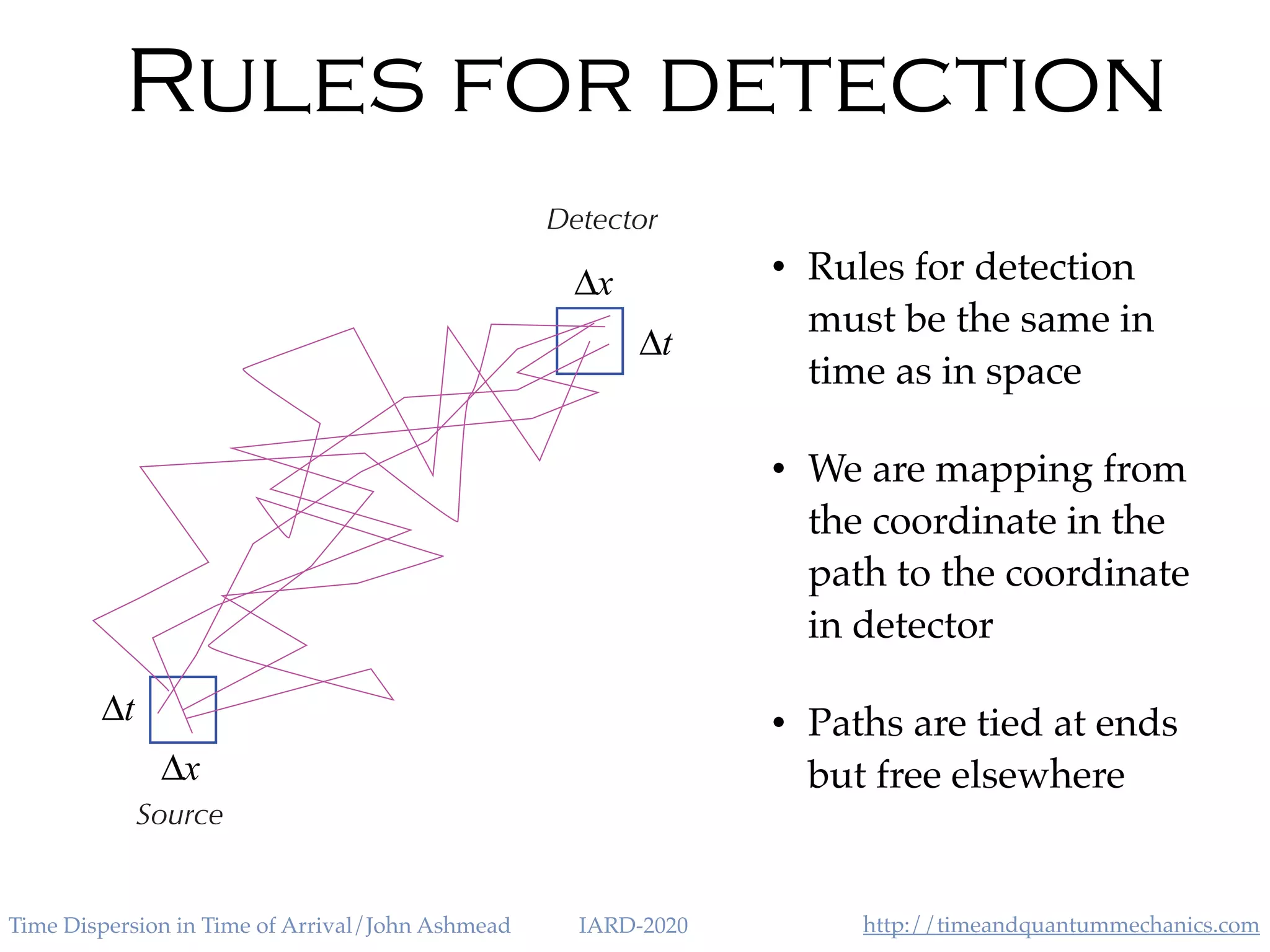
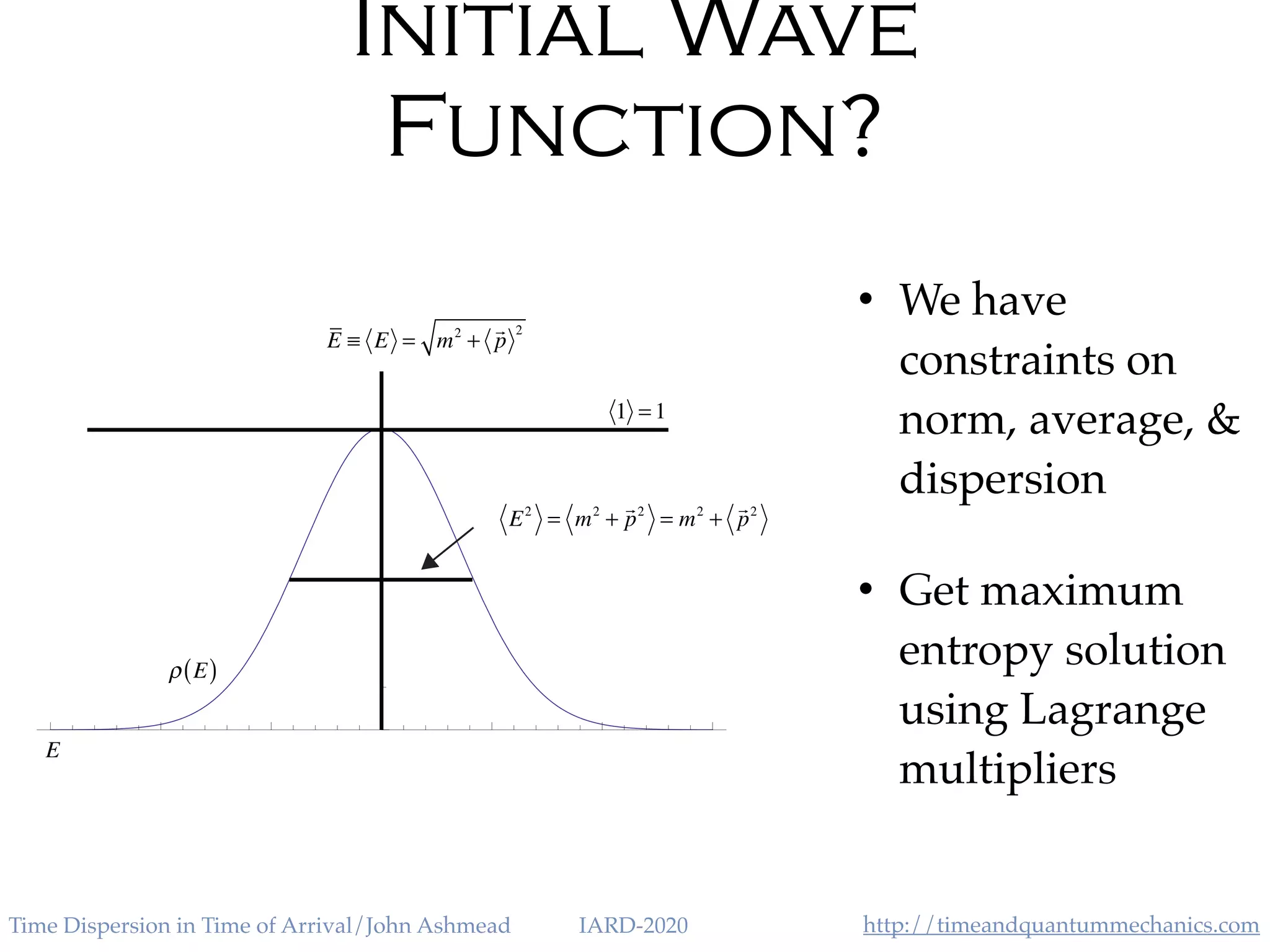
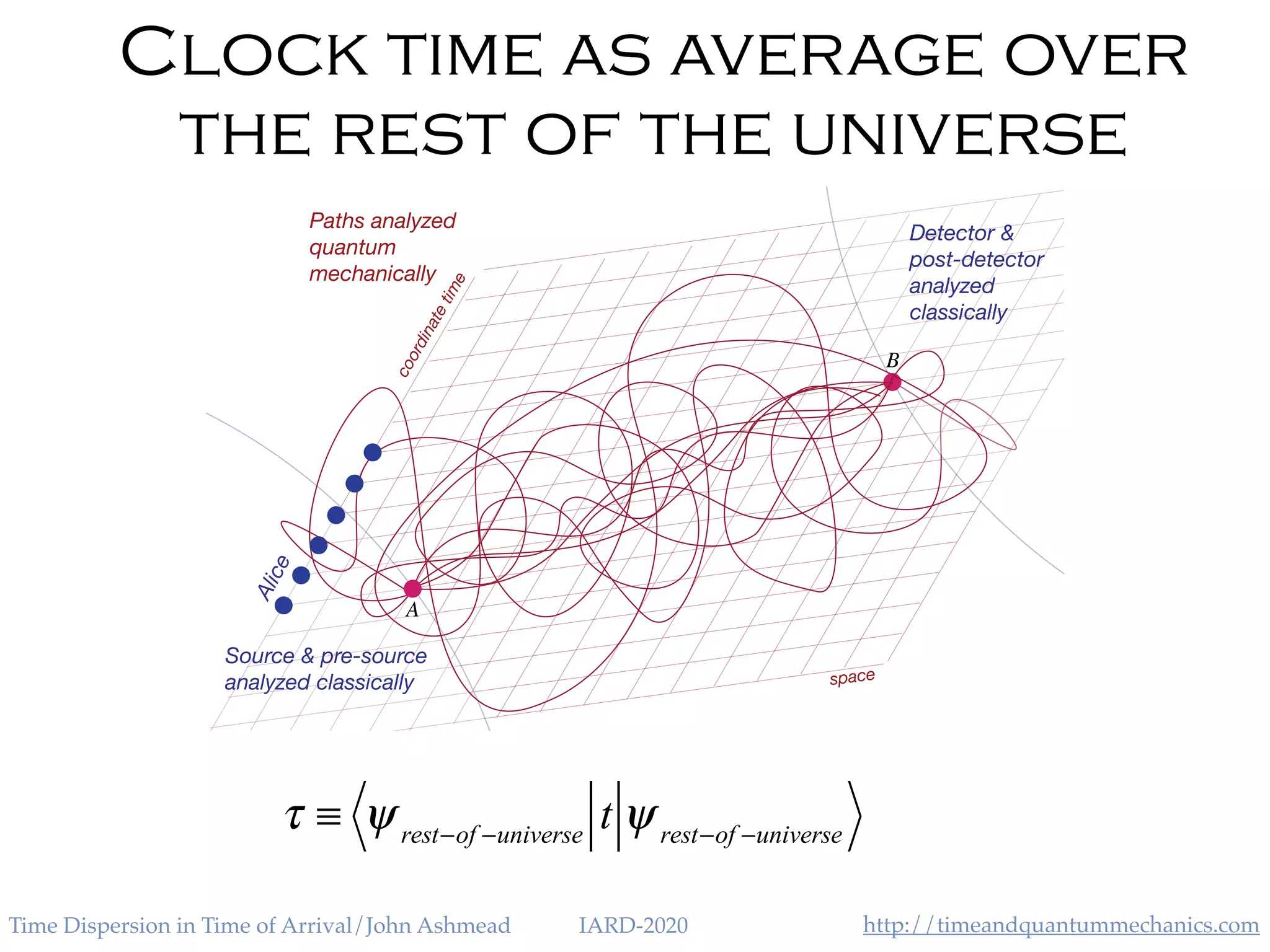
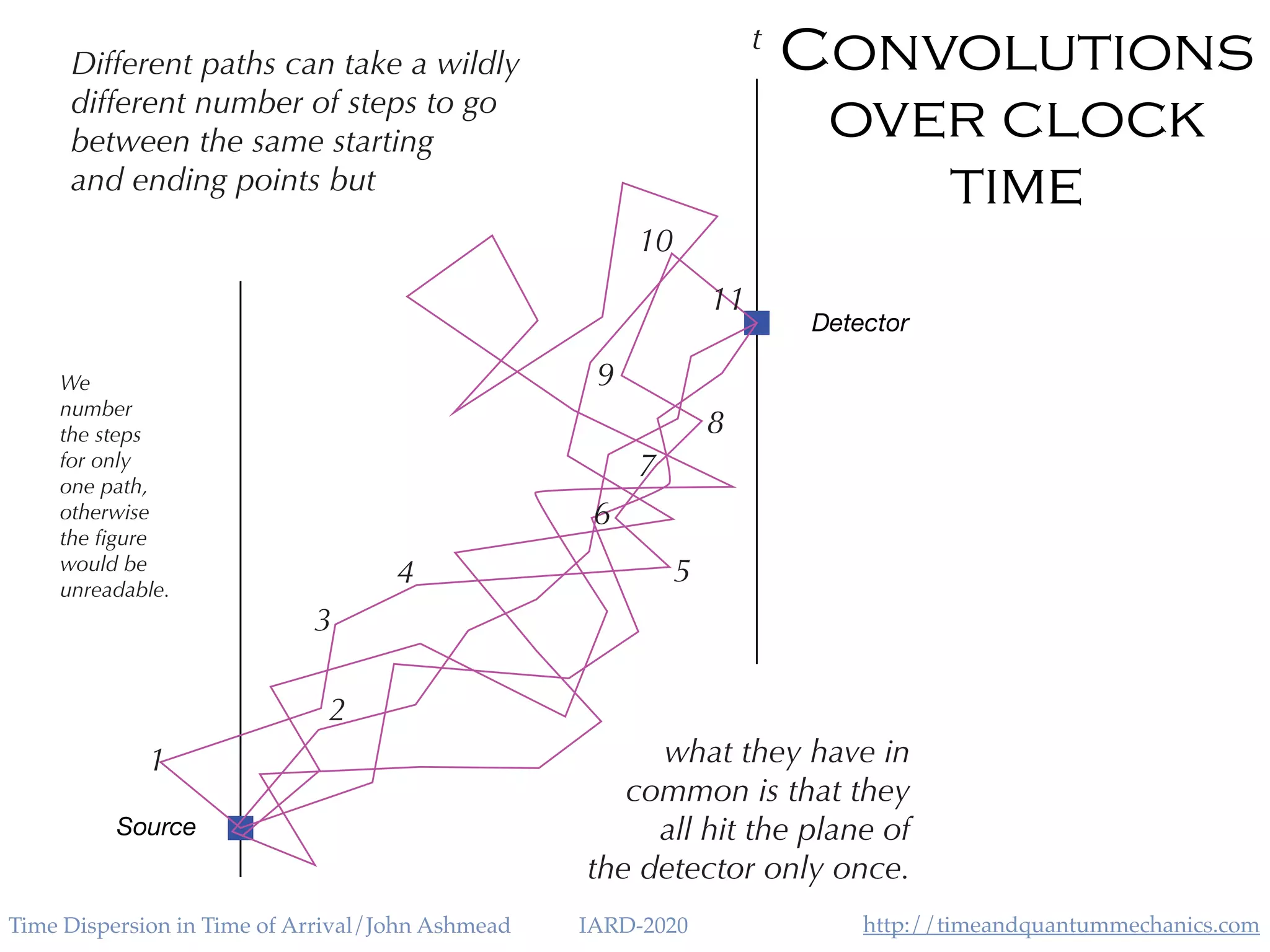
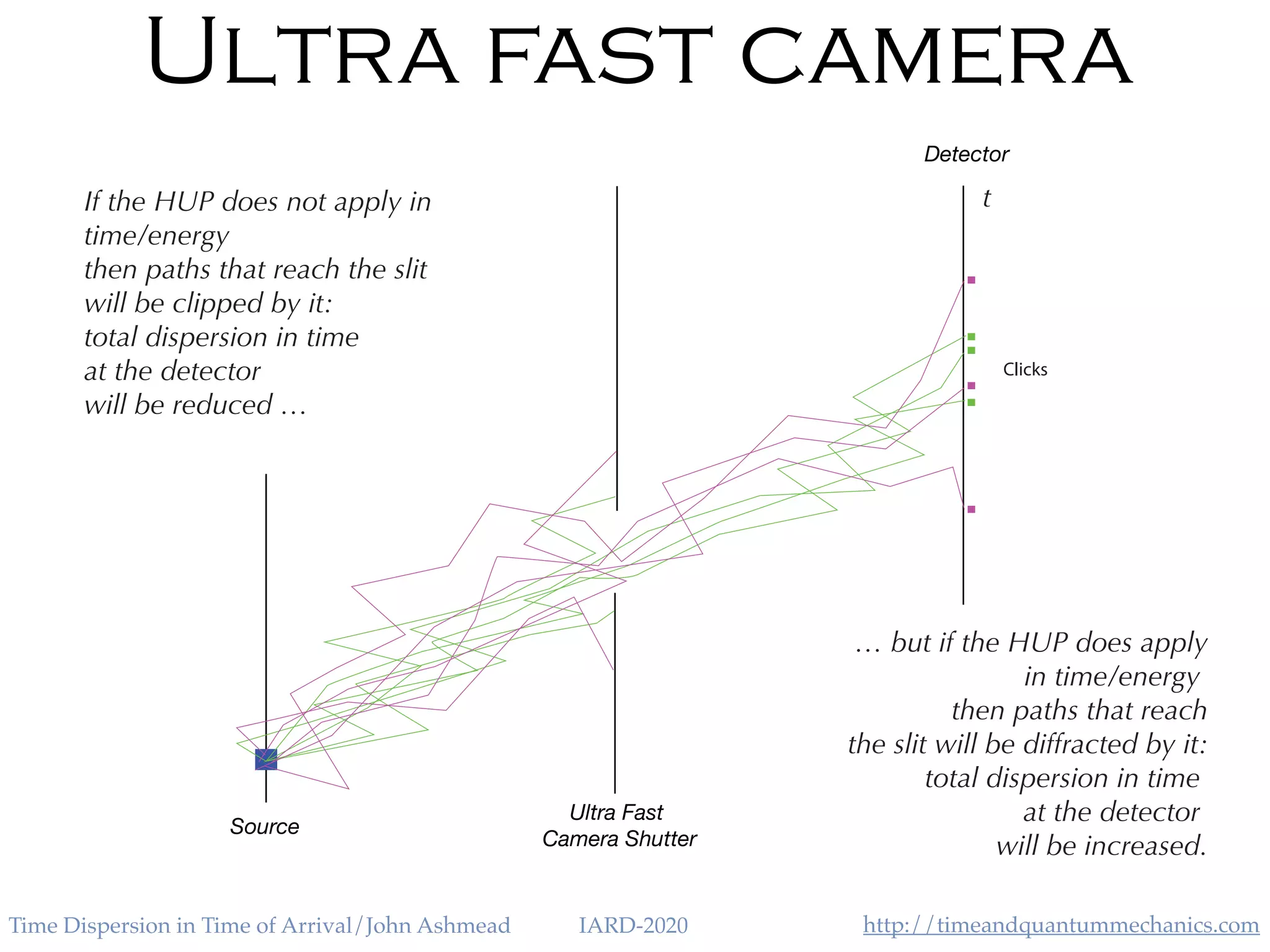
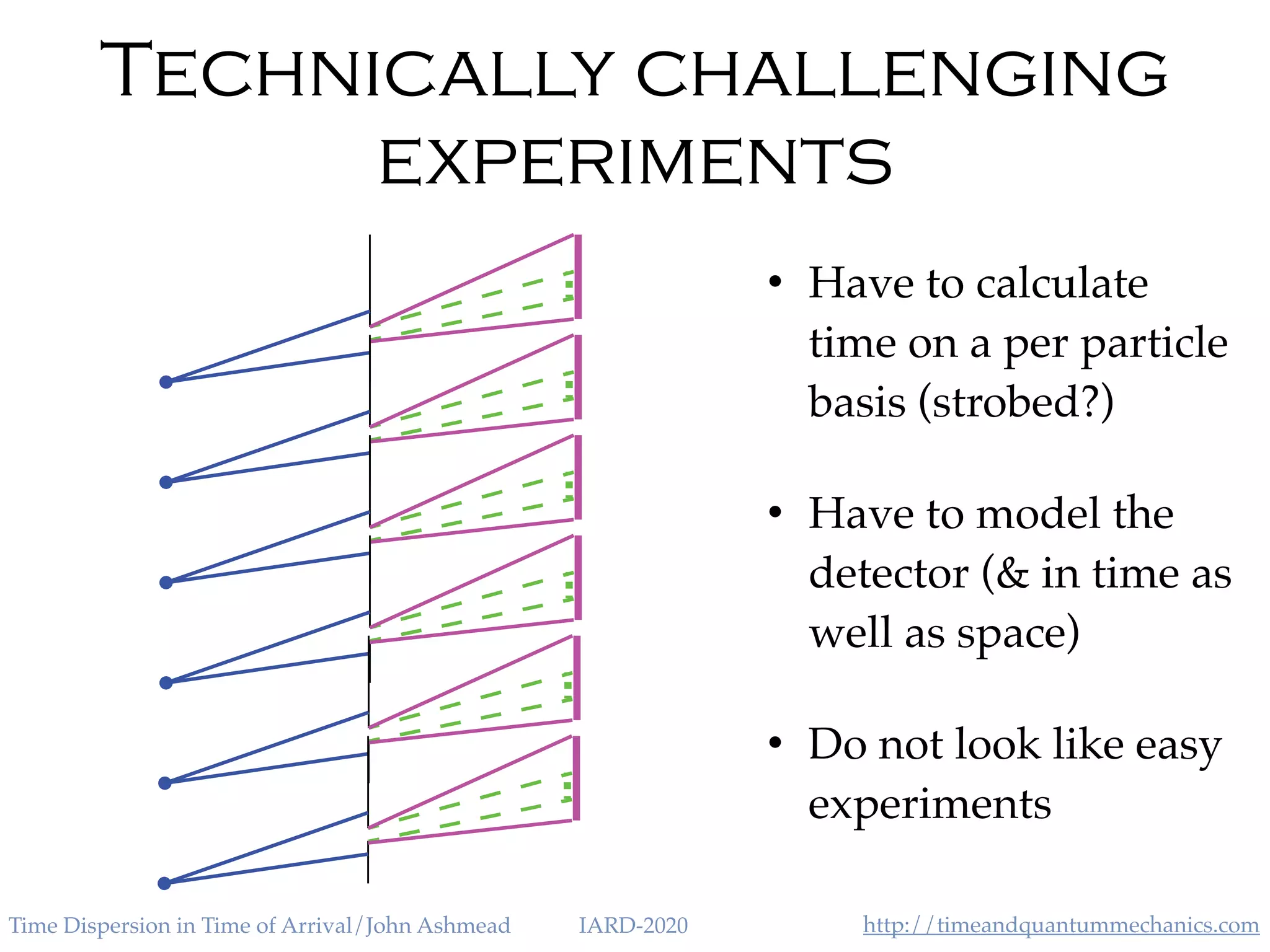
The document discusses the application of the Heisenberg uncertainty principle (HUP) in the context of time and energy, questioning whether it applies similarly to space and momentum. It explores various concepts such as time of arrival, quantum measurement, and the effects of quantum mechanics on time dispersion, ultimately suggesting experimental approaches to validate these theories. The author emphasizes the significance of time as an observable and presents potential implications for future technologies and scientific understanding.