Download as PDF, PPTX
Uploaded byRambabu Kandepu
Thesis Presentation
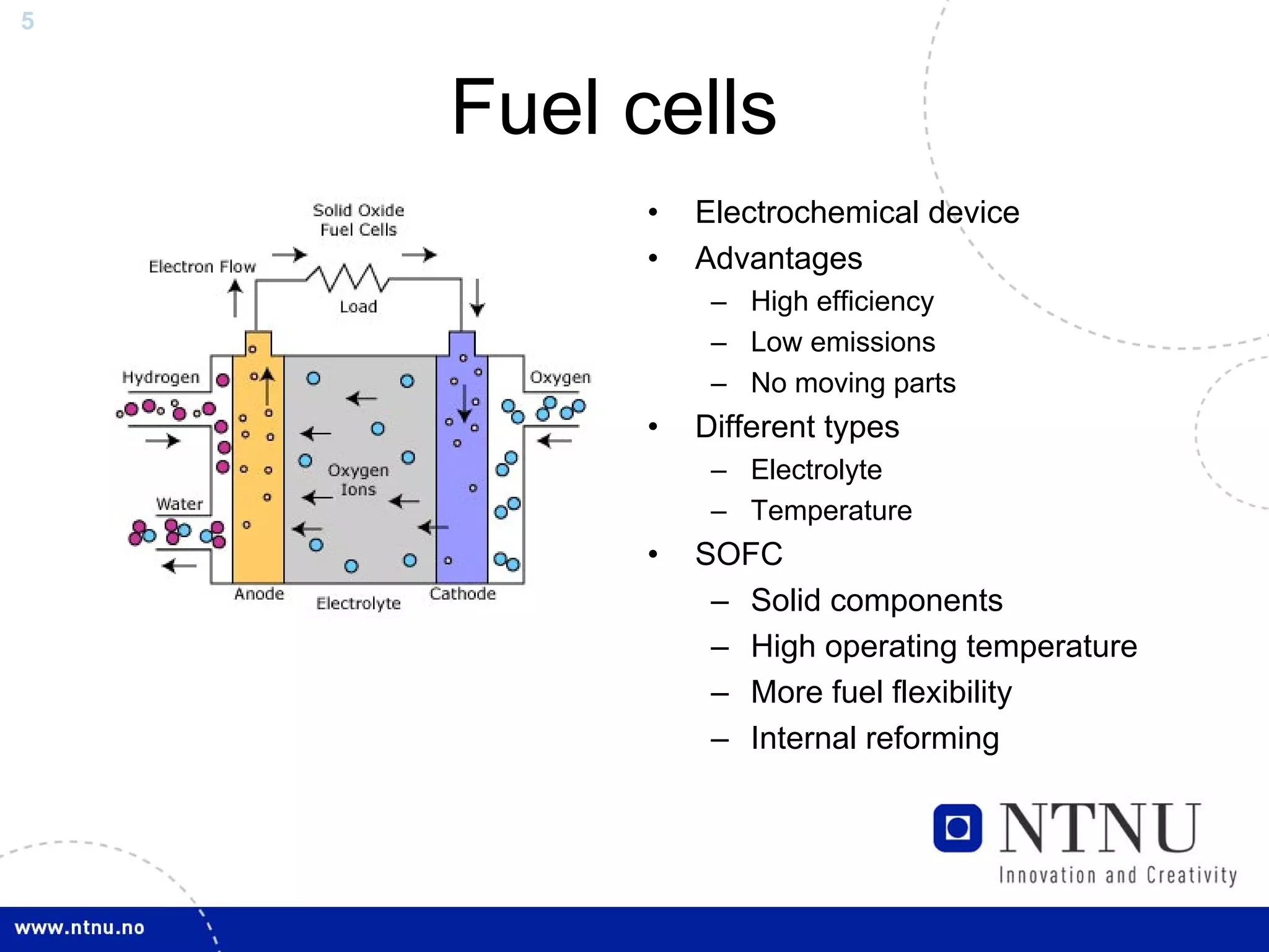
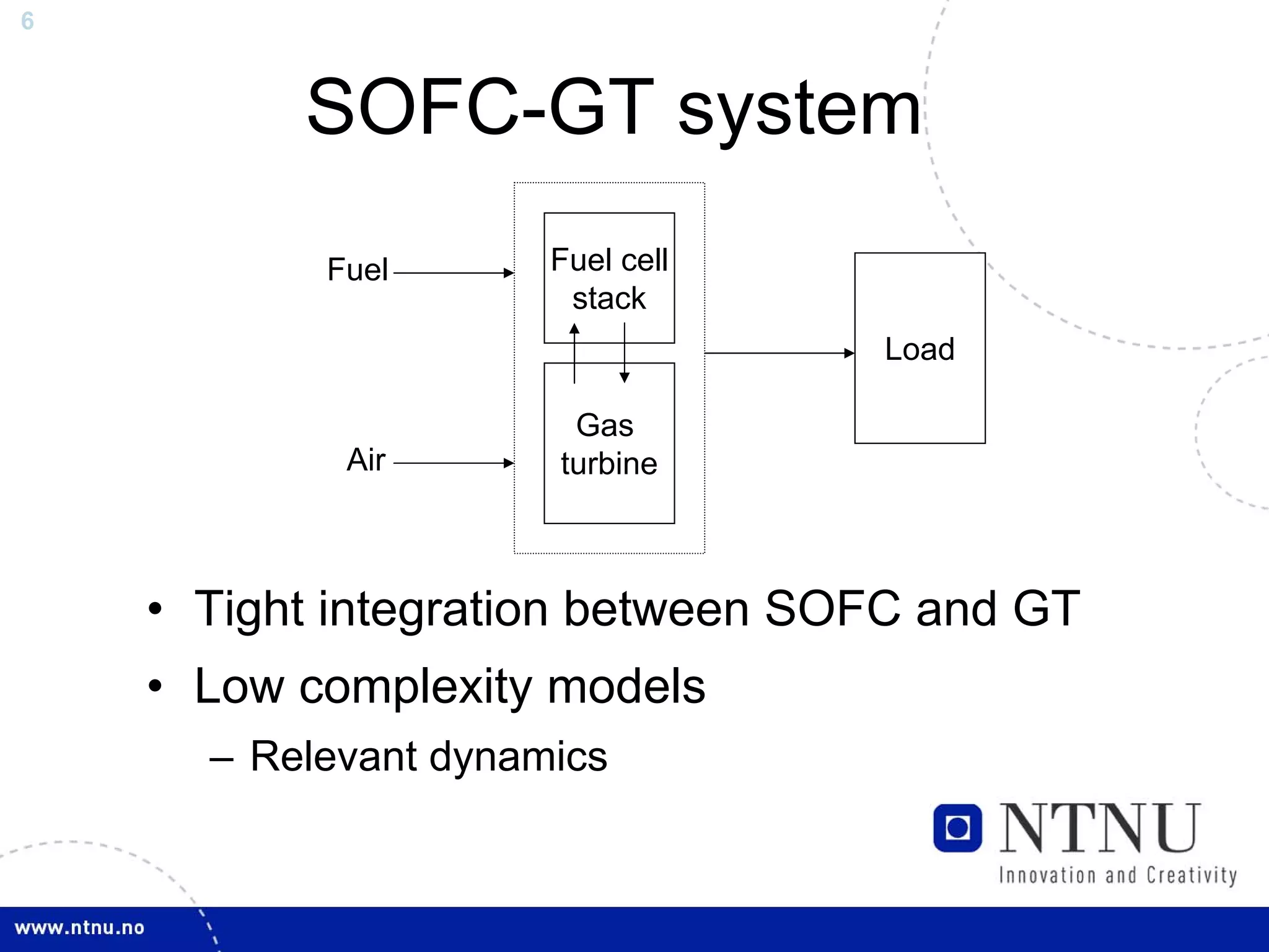
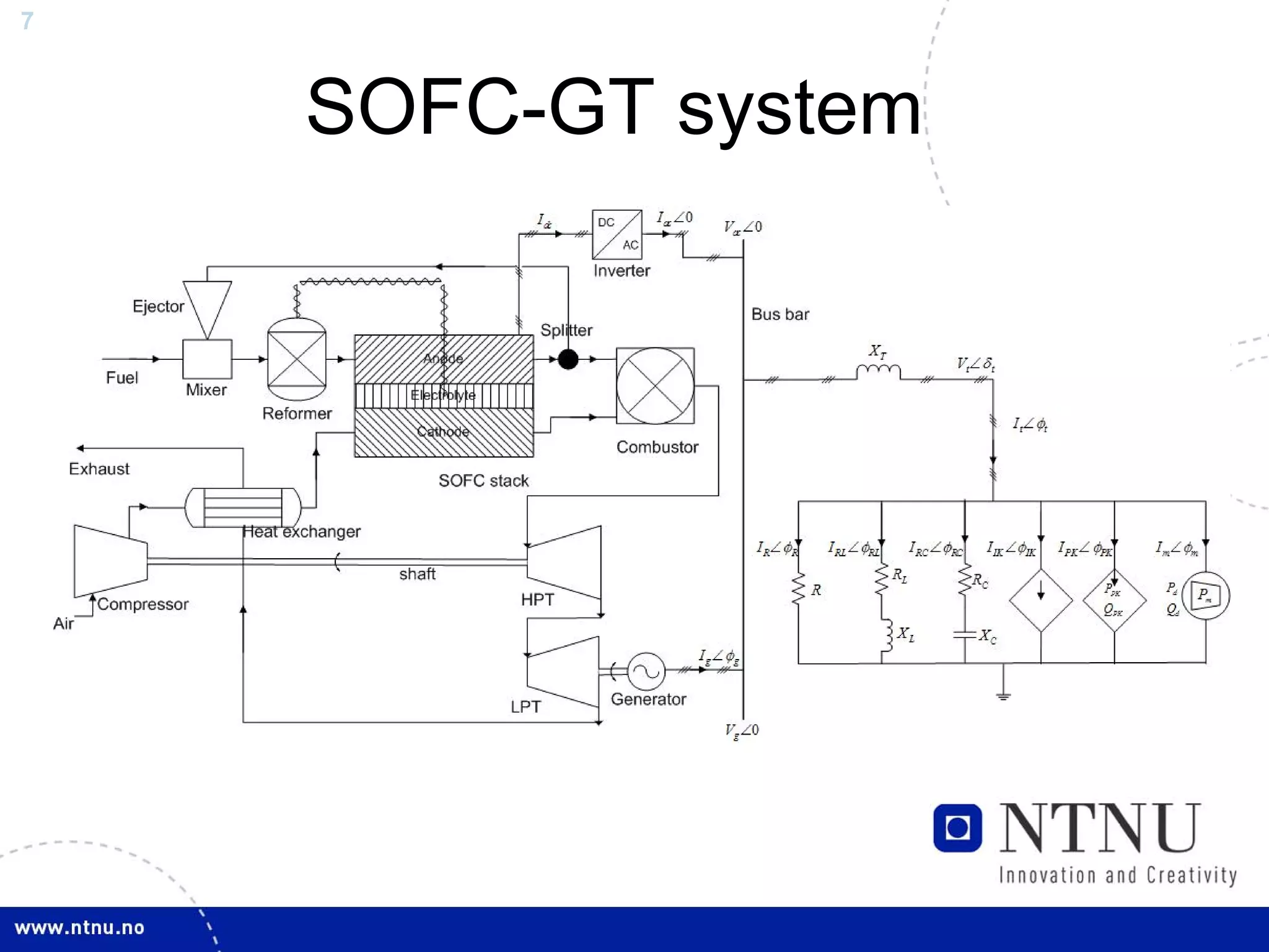
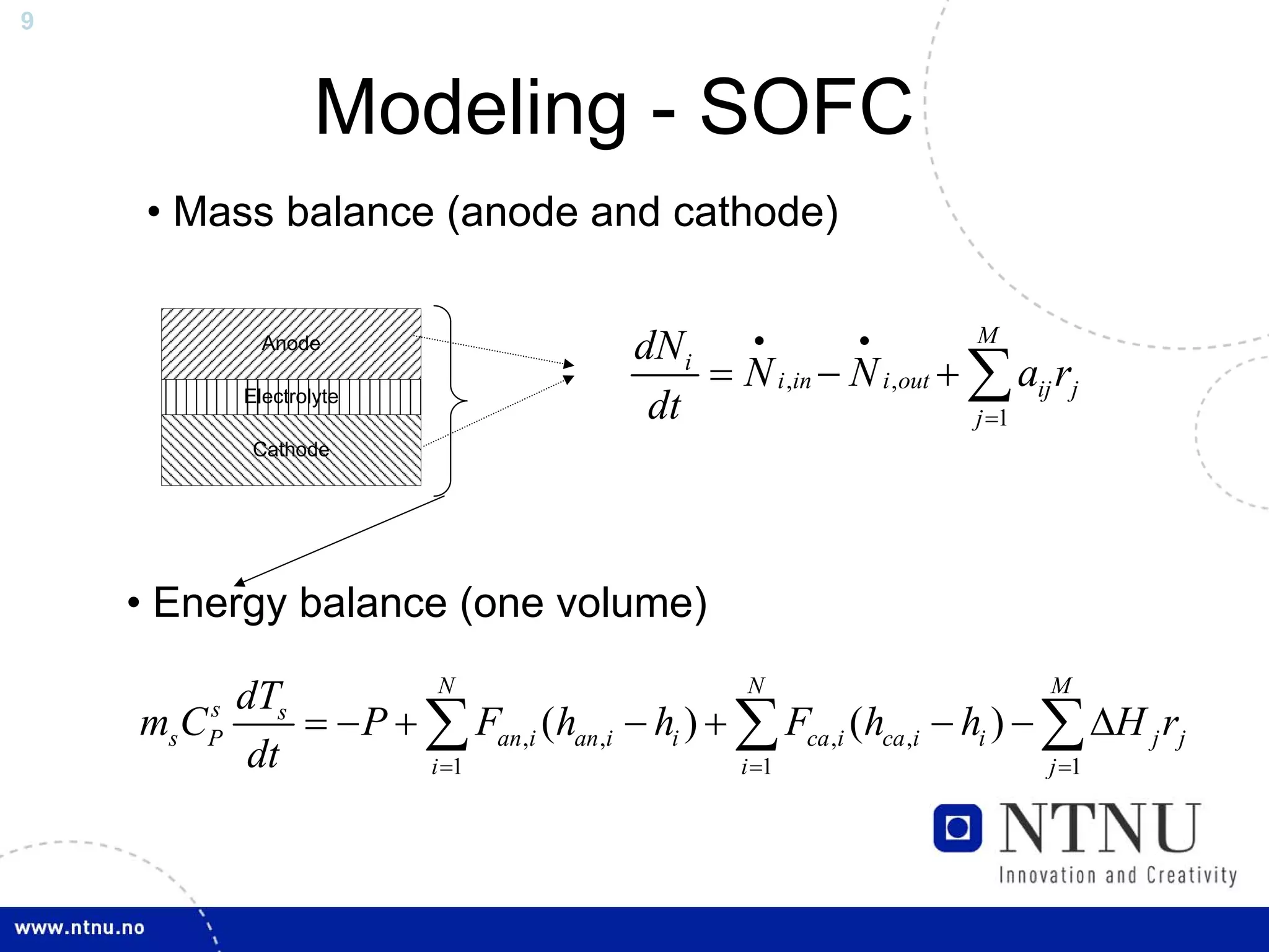
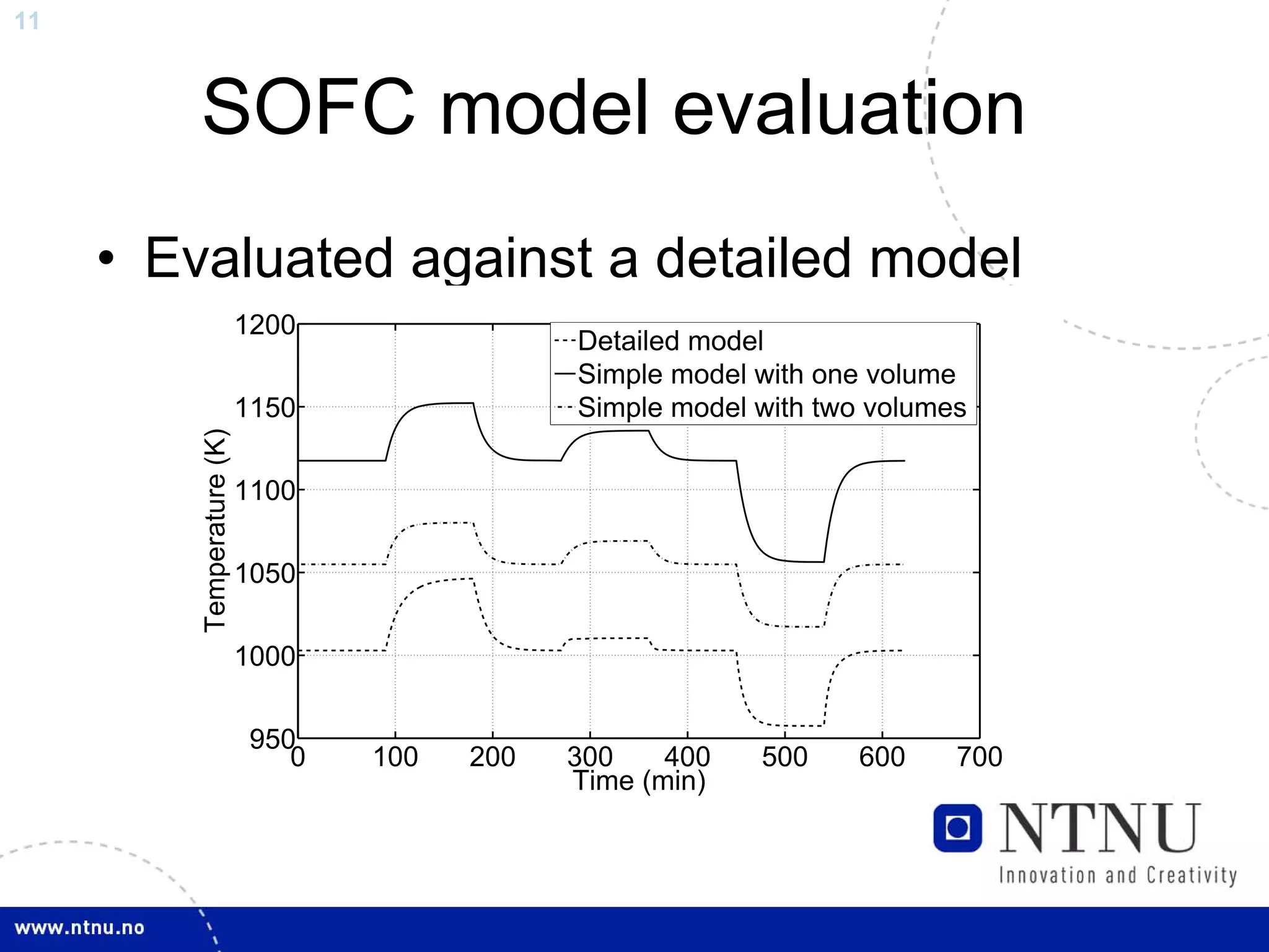
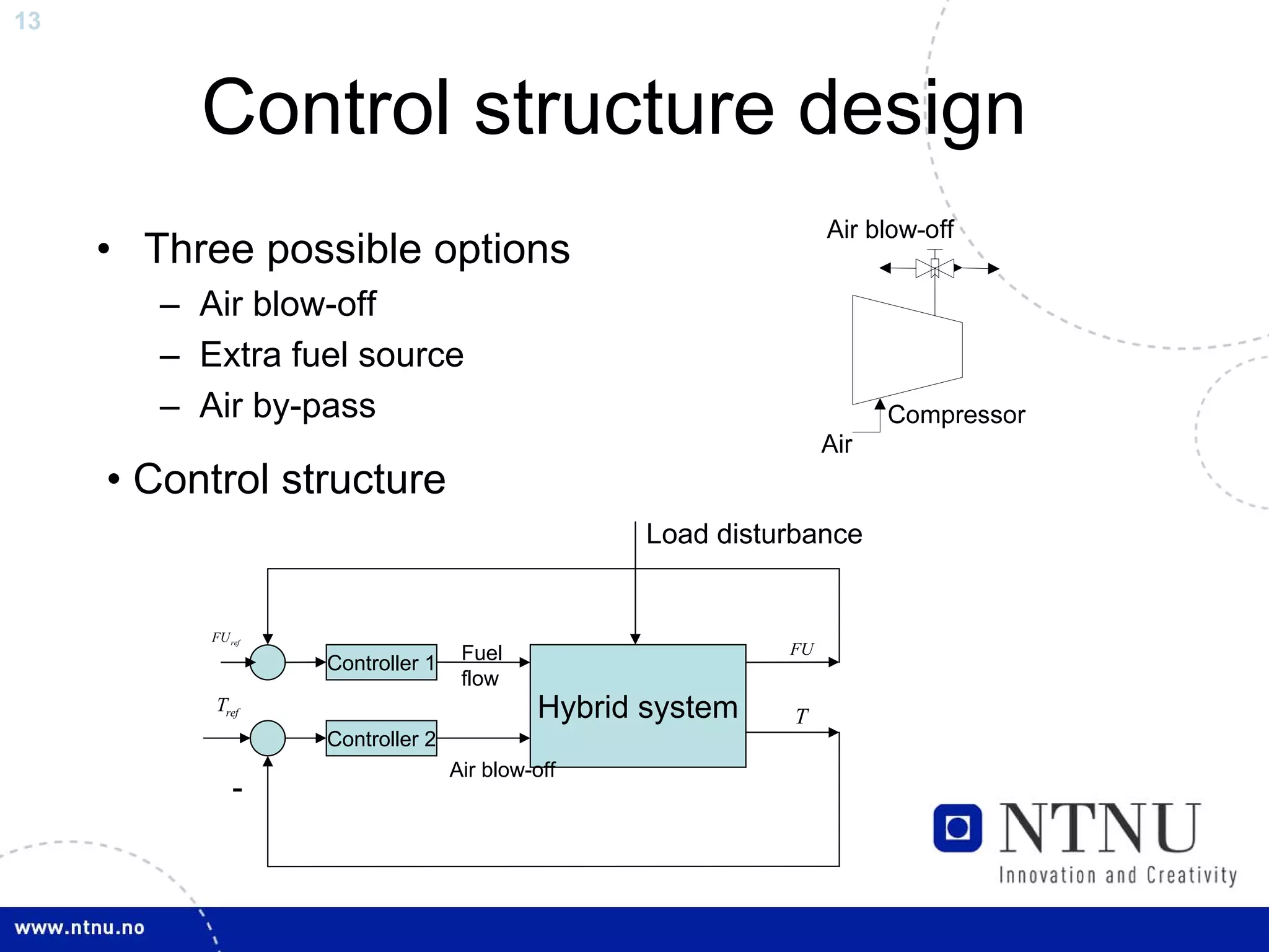
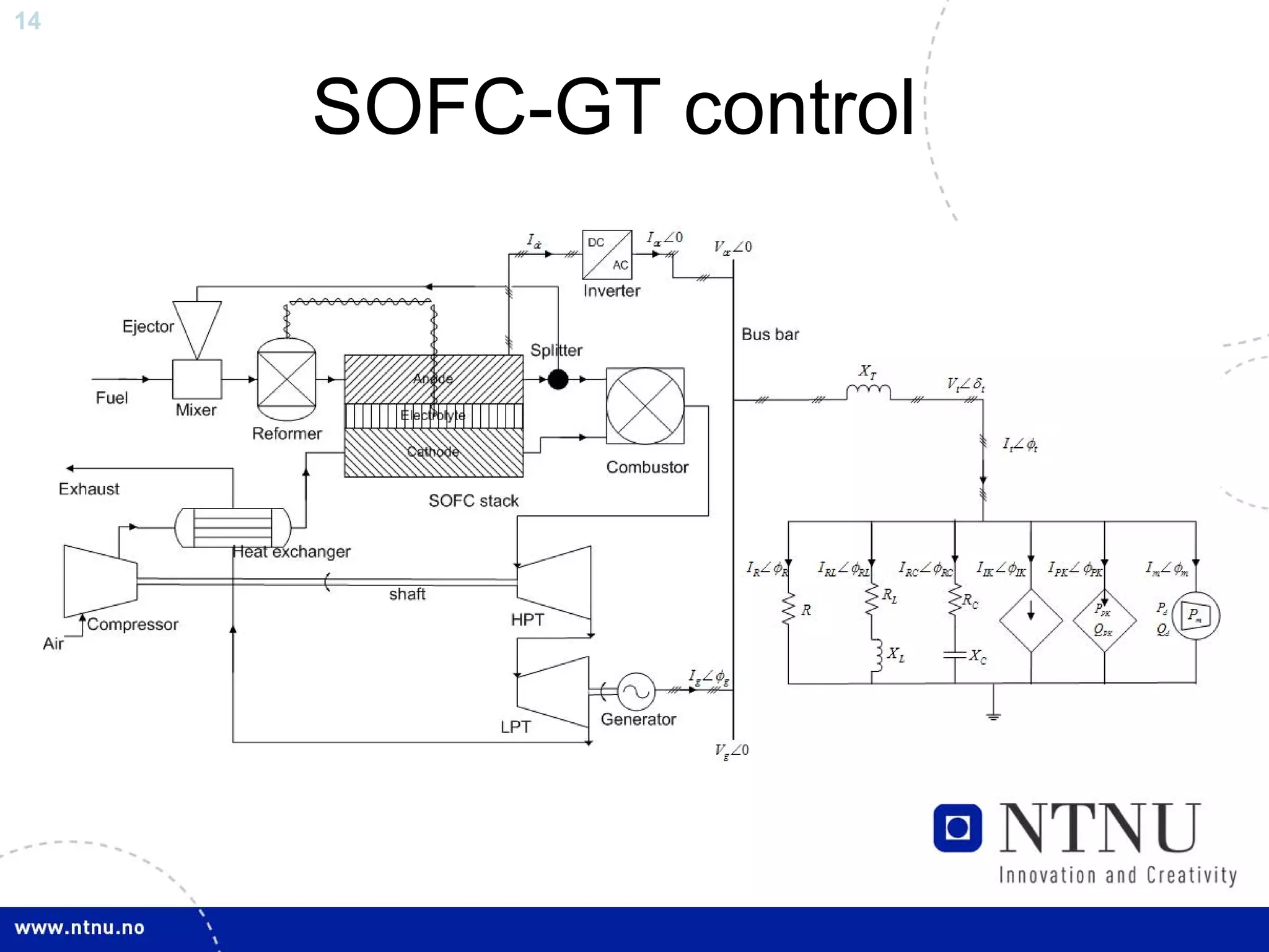
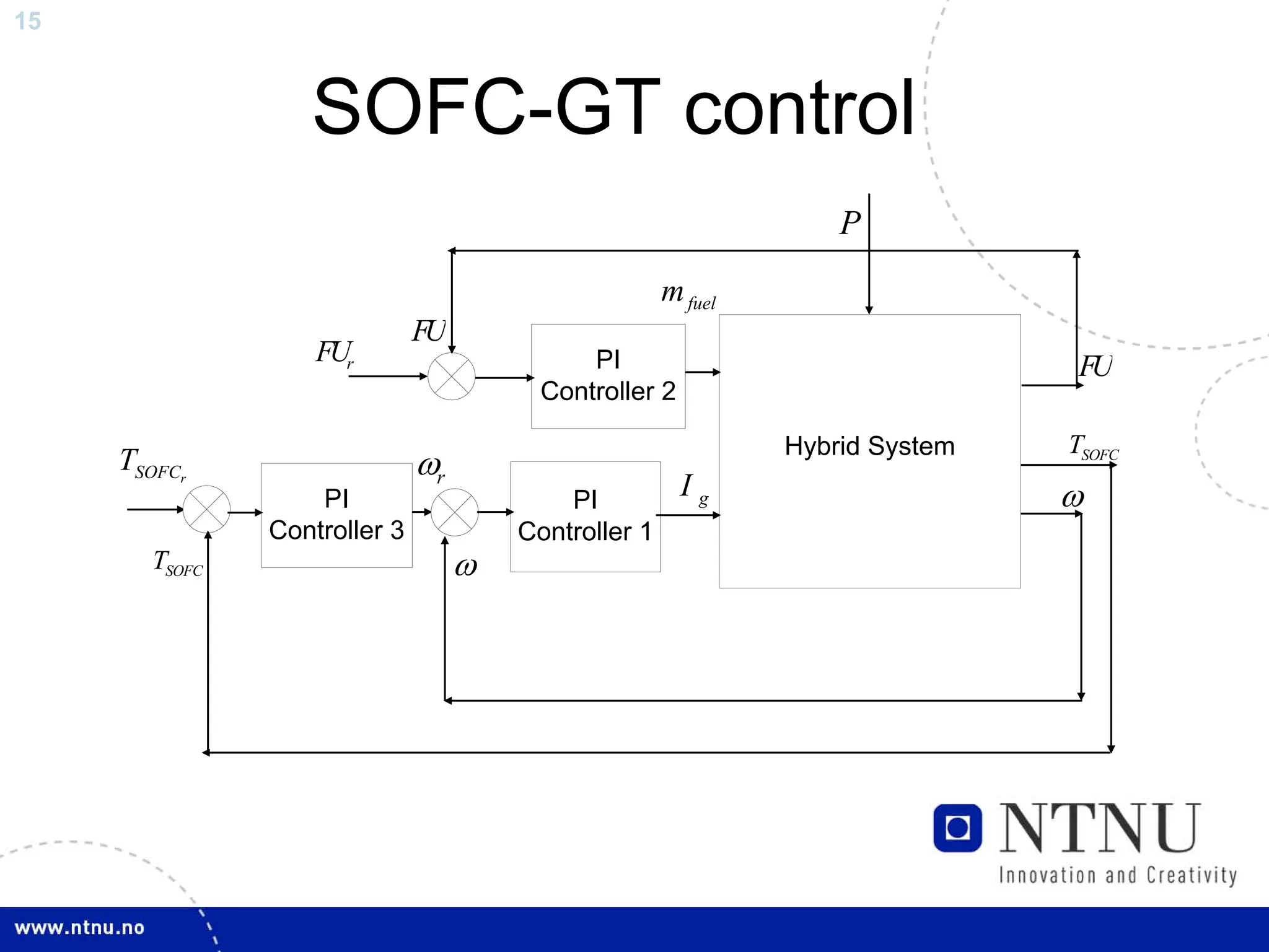
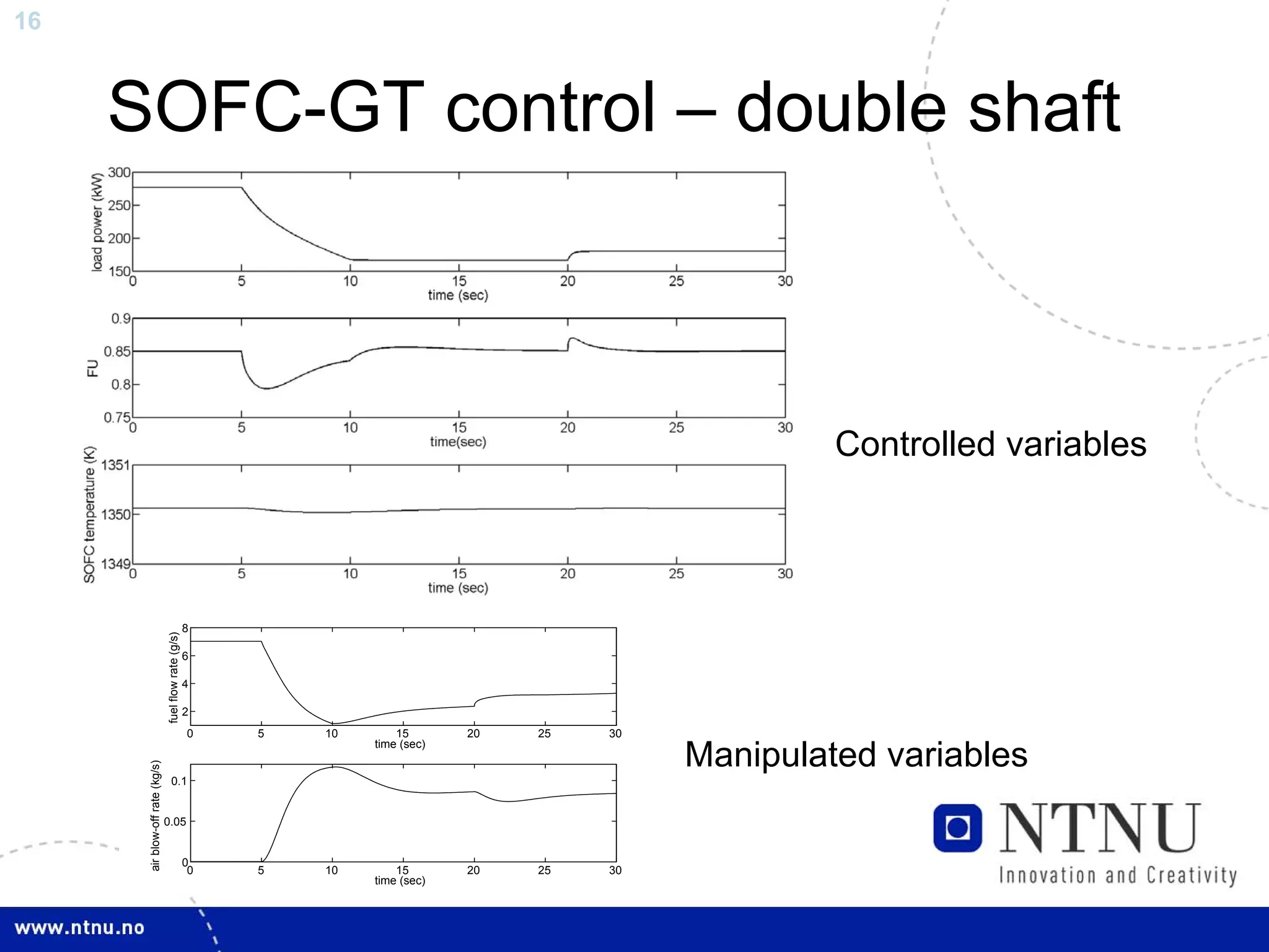
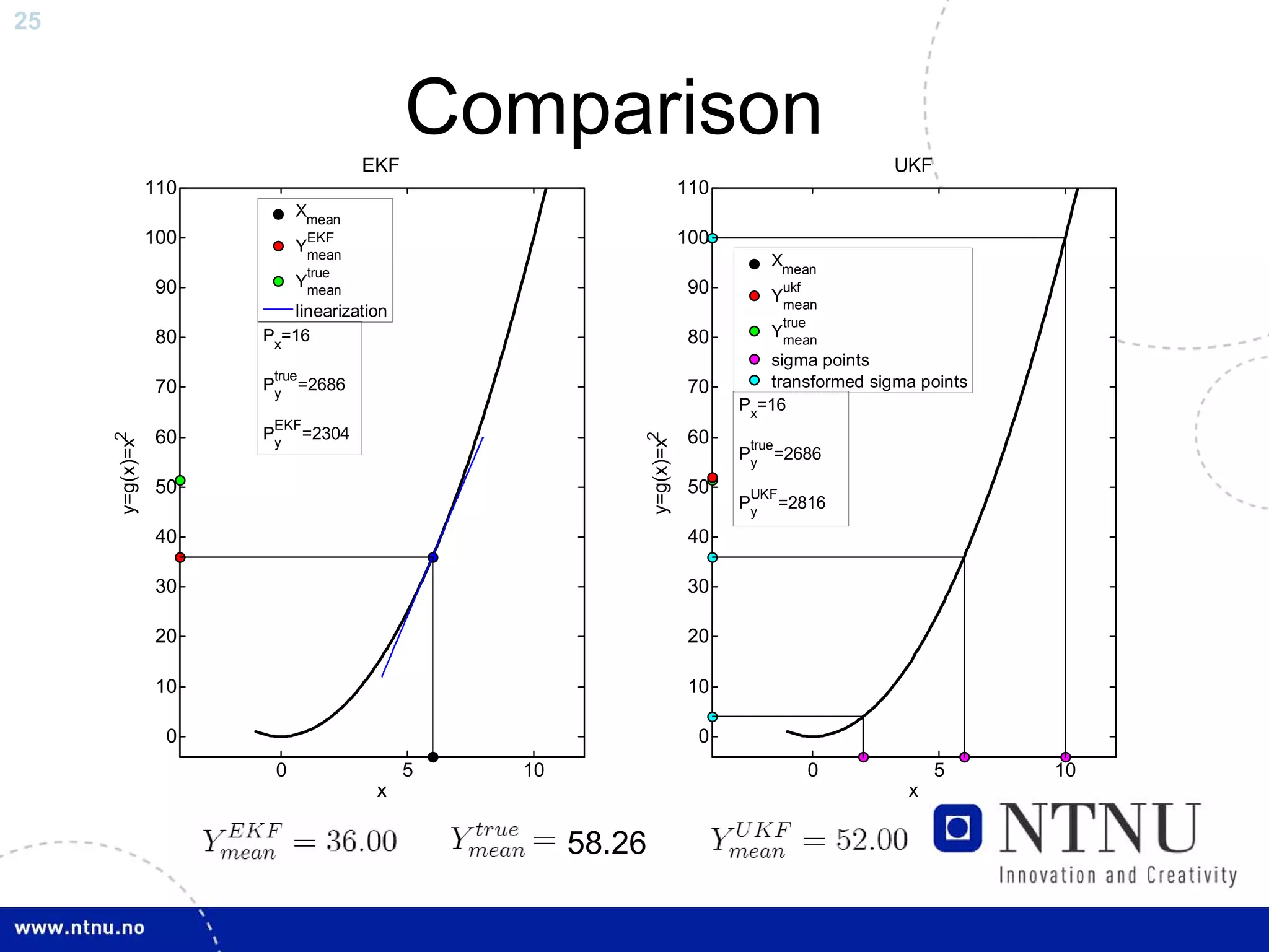
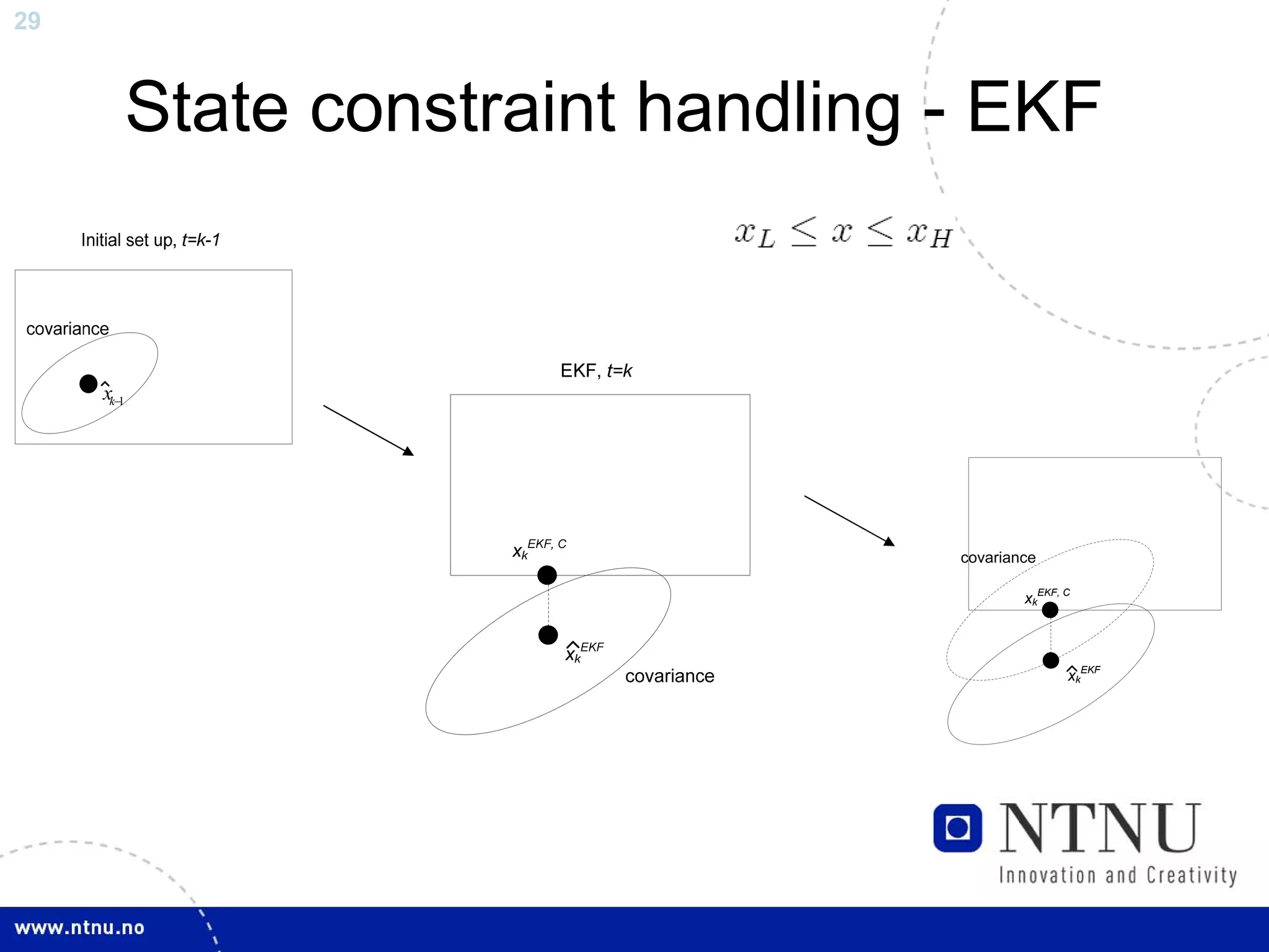
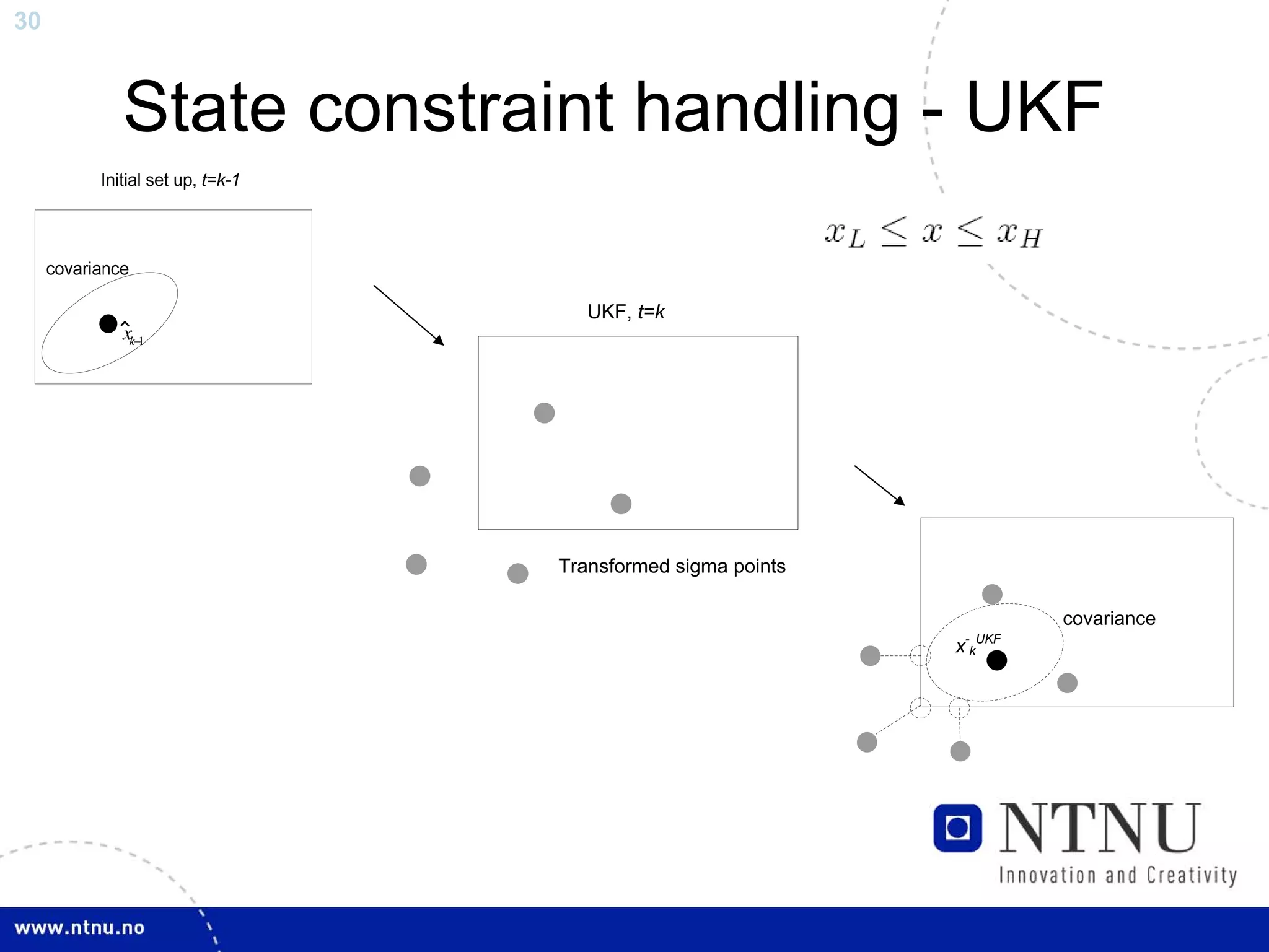
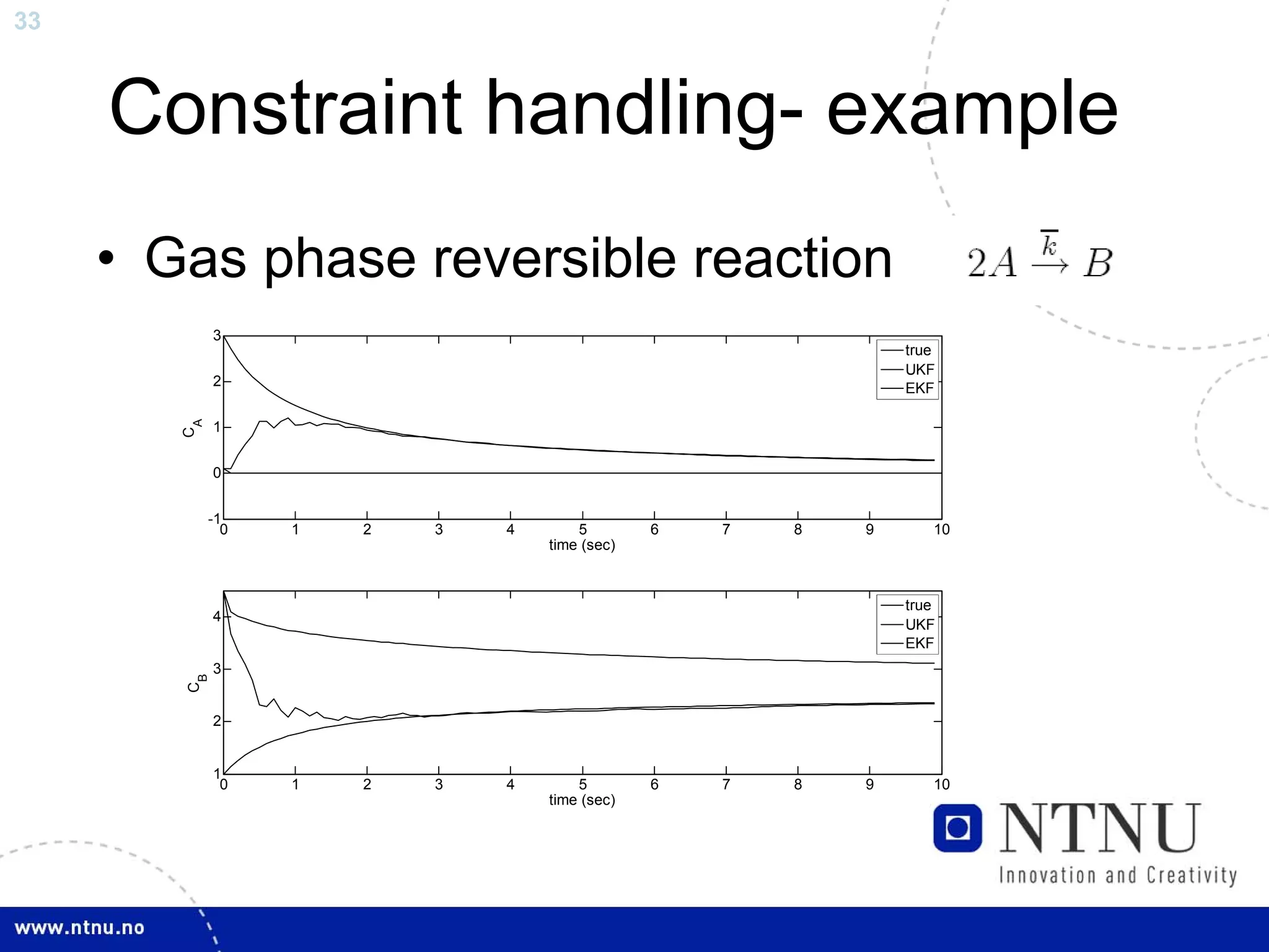
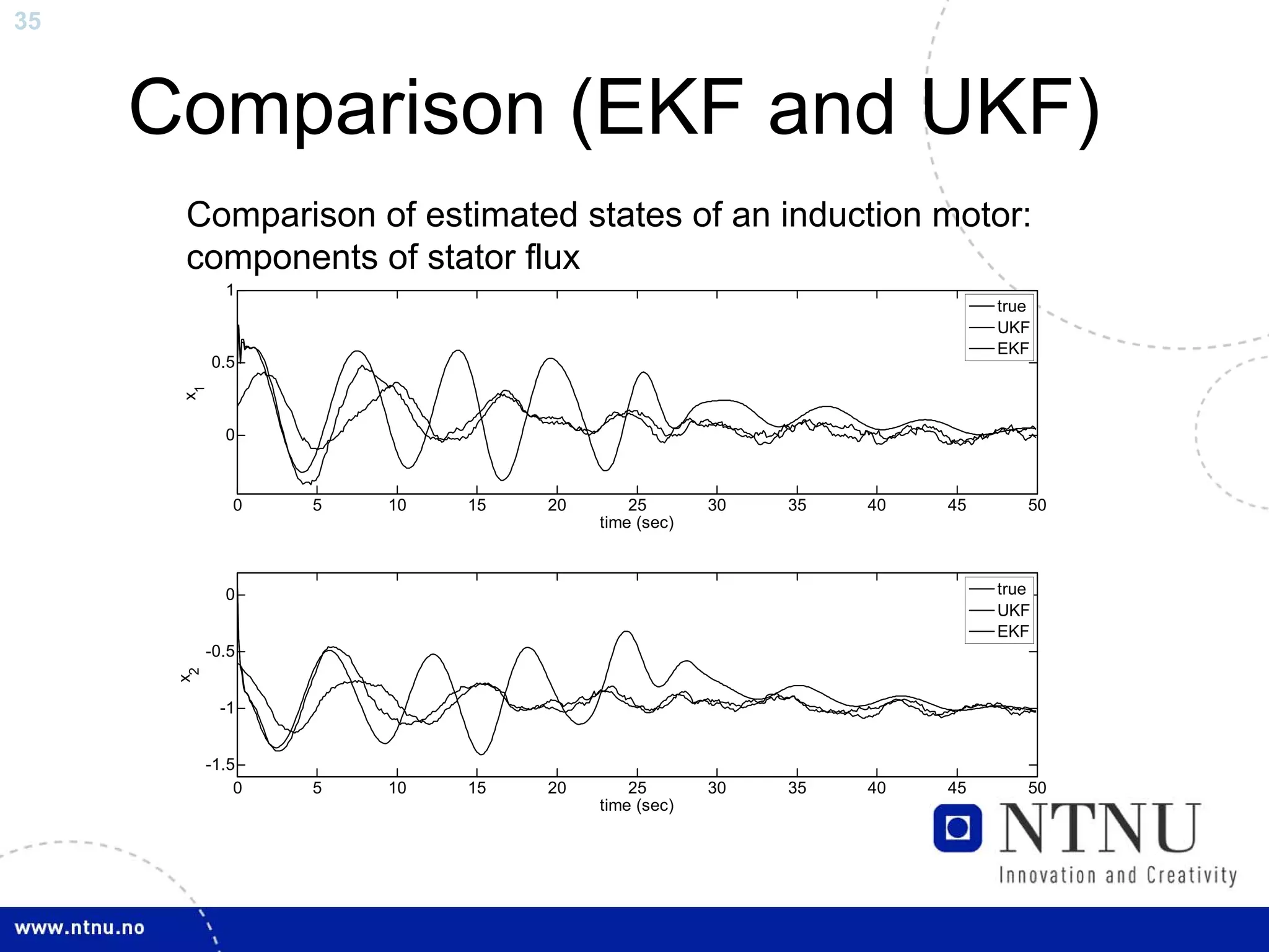
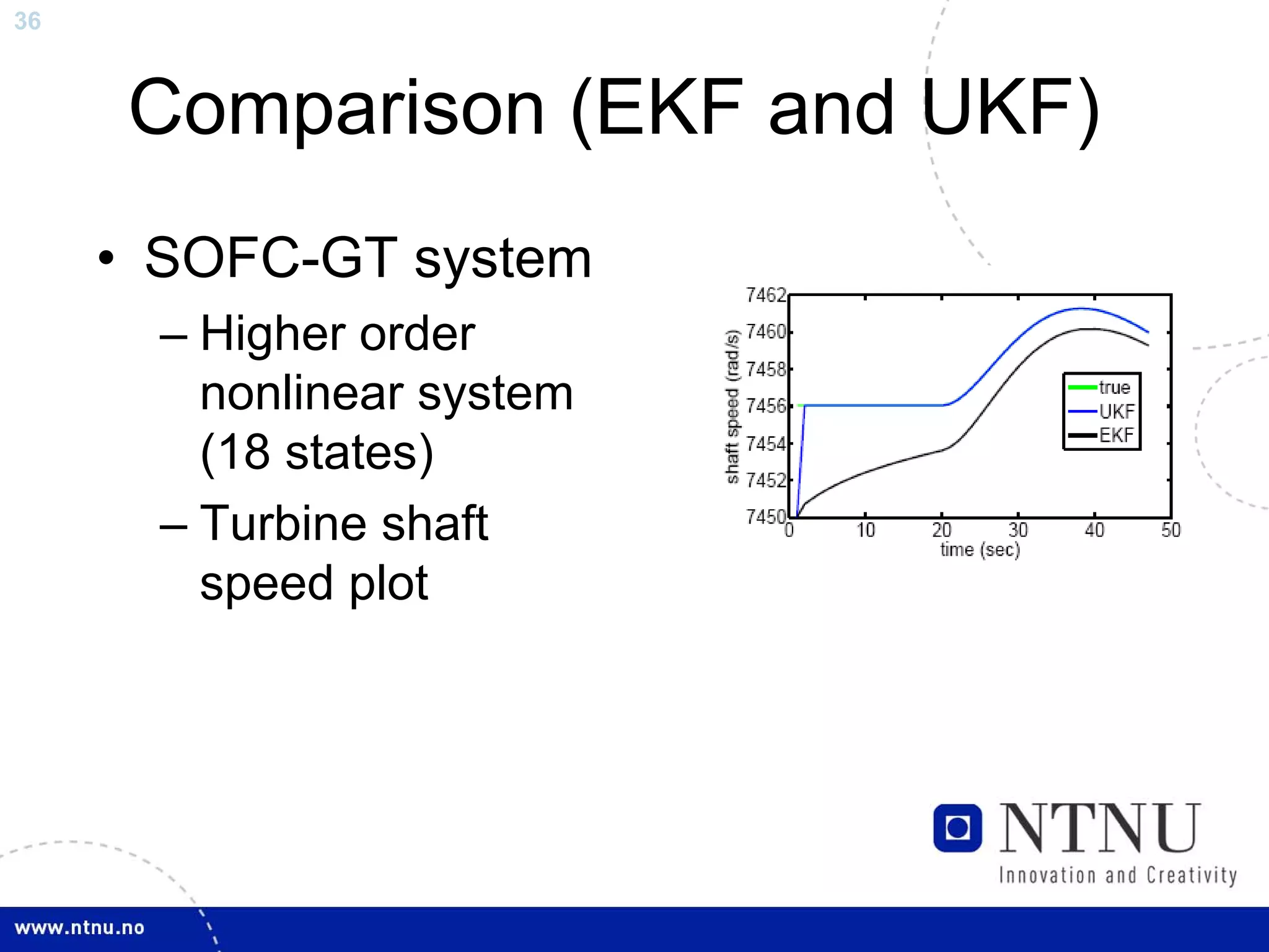
The document discusses control and state estimation techniques applied to solid oxide fuel cell-gas turbine (SOFC-GT) power systems. It motivates modeling and control of SOFC-GT systems to meet increasing energy demands efficiently with low emissions. Nonlinear state estimation using the Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) is examined. The UKF is found to provide faster state estimation convergence and better robustness to model errors compared to the EKF for nonlinear systems like the SOFC-GT.
Thesis Presentation
- 1. 1 Control relevant modeling and nonlinear state estimation applied to SOFC-GT power systems Rambabu Kandepu 04-12-2007
- 2. 2 Contents • Motivation • Modeling and control of SOFC-GT power system • Nonlinear state estimation • Conclusions
- 3. 3 Motivation • Increase in energy demand – Population growth – Industrialization • Dependency on oil and gas • Global warming
- 4. 4 Motivation • Solution to energy demand increase – Efficient of energy conversion – Technology with low emissions – Using renewable energy sources • Distributed generation – Avoid transmission and distribution losses – Wind turbines, biomass, small scale hydro, fuel cells etc
- 5. 5 Fuel cells • Electrochemical device • Advantages – High efficiency – Low emissions – No moving parts • Different types – Electrolyte – Temperature • SOFC – Solid components – High operating temperature – More fuel flexibility – Internal reforming
- 6. 6 SOFC-GT system Fuel Fuel cell stack Load Gas Air turbine • Tight integration between SOFC and GT • Low complexity models – Relevant dynamics
- 7. 7 SOFC-GT system
- 8. 8 Modeling - SOFC • Assumptions – All variables are uniform – Thermal inertia of gases is neglected – Pressure losses are neglected for energy balance – Ideal gas behavior • Reactions CH 4 + H 2O ⇔ CO + 3H 2 1 O + 2e − → O 2 − 2 2 CO + H 2O ⇔ CO2 + H 2 2− − H2 + O → H 2 O + 2e CH 4 + 2 H 2O ⇔ CO2 + 4 H 2
- 9. 9 Modeling - SOFC • Mass balance (anode and cathode) dN i • • M = N i ,in − N i ,out + ∑ aij rj Anode Electrolyte dt j =1 Cathode • Energy balance (one volume) N N M dTs ms C s P = − P + ∑ Fan ,i (han ,i − hi ) + ∑ Fca ,i (hca ,i − hi ) − ∑ ΔH j rj dt i =1 i =1 j =1
- 10. 10 Modeling - SOFC • Voltage RT ⎛ pH 2 pO22 ⎞ 1 E = E0 + ln ⎜ ⎟ V = E − Vloss 2 F ⎜ pH 2O ⎝ ⎟ ⎠ • Fuel Utilization (FU) = fuel utilized / fuel supplied • Distributed nature of SOFC • All models are developed in gPROMS Fuel Anode inlet Anode outlet Anode inlet Anode outlet Volume − I Volume − II Air Cathode inlet Cathode outlet Cathode inlet Cathode outlet
- 11. 11 SOFC model evaluation • Evaluated against a detailed model 1200 Detailed model Simple model with one volume 1150 Simple model with two volumes Temperature (K) 1100 1050 1000 950 0 100 200 300 400 500 600 700 Time (min)
- 12. 12 Control structure design • Dynamic load operation is necessary • Manipulated variable (1) – Fuel flow rate • Controlled variables (2) – Fuel utilization (FU) – SOFC temperature • Load as a disturbance • Need for a process redesign
- 13. 13 Control structure design • Three possible options – Air blow-off – Extra fuel source – Air by-pass • Control structure Load disturbance FU ref Fuel FU Controller 1 flow Tref Hybrid system T Controller 2 Air blow-off -
- 14. 14 SOFC-GT control
- 15. 15 SOFC-GT control P m fuel FU FUr PI FU Controller 2 Hybrid System TSOFC TSOFCr ωr PI PI Ig ω Controller 3 Controller 1 TSOFC ω
- 16. 16 SOFC-GT control – double shaft Controlled variables 8 fuel flow rate (g/s) 6 4 2 0 5 10 15 20 25 30 time (sec) Manipulated variables air blow-off rate (kg/s) 0.1 0.05 0 0 5 10 15 20 25 30 time (sec)
- 17. 17 SOFC-GT control • Model Predictive Control (MPC) to include constraints – FU – Steam to carbon ratio – SOFC temperature change • Not all states are measurable • State estimation is necessary
- 18. 18 State estimation • Need for state estimation • Nonlinear state estimation – Extended Kalman Filter (EKF) – Unscented Kalman Filter (UKF) – Comparison – Constraint handling – Results • Conclusions
- 19. 19 State estimation • Important for process control and performance monitoring • Uncertainties; Model, measurement and noise sources • Represent the model state by an probability distribution function (pdf) • State estimation propagates the pdf over time in some optimal way • Gaussian pdf
- 20. 20 Nonlinear state estimation • Extended Kalman Filter (EKF) – Most common way to apply KF to a nonlinear system • High order EKFs – Computationally not feasible • Ensemble Kalman Filter (EnKF) – Mostly for large scale systems (reservoir models) • Unscented Kalman Filter (UKF) – Simple and effective • Moving Horizon Estimation (MHE) – Computationally demanding
- 21. 21 EKF principle y = g ( x); x ∈ n a random vector g: n → m , nonlinear function ( How to compute the pdf of y, given the Gaussian pdf x, Px of x ?) EKF y = g ( x) PyEKF = ( ∇g ) Px ( ∇g ) T where ( ∇g ) is the Jacobian of g ( x) at x
- 22. 22 UKF principle • UKF principle y = g ( x); x ∈ n a random vector g: n → m , nonlinear function ( ) How to compute the pdf of y, given the Gaussian pdf x, Px of x ? UKF approximates the pdf. It uses true nonlinear process and observation models.
- 23. 23 UKF principle • UKF principle
- 24. 24 Comparison • Example = 58.26 = 2686
- 25. 25 EKF Comparison UKF 110 110 Xmean 100 EKF Ymean 100 Xmean true 90 Ymean 90 ukf Ymean linearization true 80 Px=16 80 Ymean sigma points true transformed sigma points 70 Py =2686 70 Px=16 EKF 60 Py =2304 60 y=g(x)=x2 y=g(x)=x2 true Py =2686 50 50 UKF Py =2816 40 40 30 30 20 20 10 10 0 0 0 5 10 0 5 10 x x 58.26
- 26. 26 Algorithms: EKF and UKF Nonlinear system
- 27. 27 Algorithms: EKF and UKF EKF UKF Prediction step: Calculate Jacobians / sigma points transformation Prediction step: Calculate mean and covariance Correction step: Calculate Jacobians/ sigma points transformation Correction step: Kalman update equations
- 28. 28 State constraint handling • No general way in KF theory – Projecting unconstrained state estimate onto boundary • Systematic approach in MHE – Solving a nonlinear problem at each time step • A simple method is introduced in UKF
- 29. 29 State constraint handling - EKF xk−1 covariance xkEKF, C xkEKF
- 30. 30 State constraint handling - UKF UKF, t=k xk−1 Transformed sigma points covariance x-kUKF
- 31. 31 Constraint handling
- 32. 32 Constraint handling UKF • Constraint handling method – Projections at different steps • Sigma points • Transformed sigma points • Transformed sigma points through measurement function – Inequality constraints
- 33. 33 Constraint handling- example • Gas phase reversible reaction 3 true UKF 2 EKF A 1 C 0 -1 0 1 2 3 4 5 6 7 8 9 10 time (sec) true 4 UKF EKF 3 B C 2 1 0 1 2 3 4 5 6 7 8 9 10 time (sec)
- 34. 34 Comparison (EKF and UKF) • Nonlinear systems – Induction motor and Van der Pol Oscillator – Faster convergence with UKF • Robustness to model errors – Van der Pol oscillator • Better performance with UKF • Higher order nonlinear system – SOFC-GT hybrid system (18 states)
- 35. 35 Comparison (EKF and UKF) Comparison of estimated states of an induction motor: components of stator flux 1 true UKF EKF 0.5 1 x 0 0 5 10 15 20 25 30 35 40 45 50 time (sec) 0 true UKF EKF -0.5 2 x -1 -1.5 0 5 10 15 20 25 30 35 40 45 50 time (sec)
- 36. 36 Comparison (EKF and UKF) • SOFC-GT system – Higher order nonlinear system (18 states) – Turbine shaft speed plot
- 37. 37 Conclusions – state estimation • The UKF is a promising option – Simple and easy to implement – No need for Jacobians – Computational load is comparable to EKF – Improved performance • Faster convergence • Robustness to model errors and initial choices • Simple constraint handling method works
- 38. 38 Thank you for your attention ☺