The Golden Ladder

The Golden Ladder
By
Weixin Wu
Submitted to the Board of Mathematics/Computer Science
School of Natural and Social Sciences
In partial fulfillment of the requirements
For the degree of Bachelor of Arts
Purchase College
State University of New York
May 2015
Sponsor: Irina Shablinsky
Second Reader: Knarik Tunyan

2
Table of Contents
Abstract.............................................................................................................................................3
1. Introduction to the Golden Ladder................................................................................................4
2. Recursive Properties of the Golden Ladder....................................................................................8
2.1 Theorem 1................................................................................................................................8
2.2 Theorem 2..............................................................................................................................10
2.3 Theorem 3..............................................................................................................................12
3. More about the Golden Ladder....................................................................................................14
3.1 Spiral in the Golden Ladder....................................................................................................14
3.2 Find the End Point of the Golden Ladder...............................................................................15
3.3 The Golden Ladder in Three Dimension................................................................................16
4. A “Processing” Simulation of the Golden Ladder ........................................................................17
4.1 How the Program Works?.......................................................................................................17
4.2 Program Output.....................................................................................................................19
4.3 How to Use this Program.......................................................................................................21
4.4 Why Writing this Program?....................................................................................................21
5. Results.........................................................................................................................................21
6. References...................................................................................................................................22
7. Appendix.....................................................................................................................................23

3
Abstract
In this work, a new Euclidean structure the Golden Ladder is introduced. The Golden
Ladder was first created in visual software by applying the Golden Ratio to the diameters of
tangent circles. For this work three recursive properties of the circumference and area have
been proven, and a 2D simulation of the Golden Ladder was written in processing. The Golden
Ladder has been expanded to the third dimension, and it is possible to expand the definition to
the nth dimension. The volume will be the property of interest in the third dimension. Additional
interesting properties have been found for the Golden Ladder and are currently under
investigation.

4
1. Introduction to the Golden Ladder
I am going to introduce some facts, properties and applications of the Golden Ratio
before I get into the Golden Ladder. The Golden Ratio is one of the most famous irrational
numbers. Also known as the divine proportion, golden mean, or golden section. The term
“golden section” was first used in the textbook Die Reine Elementar-Mathematik in 1835 by
Martin Ohm. [9] Two quantities a and b are in the Golden Ratio if their ratio is same as the ratio
between the sum and the larger quantity. As shown in the equation below and figure 1 for a >
b.
𝑎 + 𝑏
𝑎
=
𝑎
𝑏
= 𝜑
The lower case Greek letter phi (φ) is used to represent the Golden Ratio. Phi (φ) is one
of the roots of the quadratic equation x2 – x – 1. The exact value of the Golden Ratio is (√5 + 1) /
2 or ca 1.6180339887… expressed as an infinite decimal number. The upper case Greek letter
phi (φ) is used to represent the reciprocal of the Golden Ratio; the exact value is (√5 -1) / 2 or ca
0.6180339887… expressed as an infinite decimal fraction.
Figure 1 The Golden Ratio

5
There is an interesting relation between the Golden Ratio and the Fibonacci sequence.
[1][4] Fibonacci sequence is an integer sequence that start with 1 and 1, and each subsequent
number is the sum of the previous two. It’s known that the limit of the ratio of two consecutive
Fibonacci numbers is φ as shown in the equation below. φ can also be expressed as exact
trigonometric formulas including 2cos (
𝜋
5
),
1
2
sec(
2𝜋
5
) and
1
2
csc(
𝜋
10
).
lim
𝑛→∞
𝐹𝑛+1
𝐹𝑛
= 𝜑
φ is the “worst” real number for rational approximation because its continued fraction
representation as shown in the equation below.
𝜑 = [1,1,1,1, … ]
𝜑 = 1 +
1
1 +
1
1 +
1
1 + ⋯
φ can also be represented in terms of a nested radical as shown below.
𝜑 = √1 + √1 + √1 + ⋯
The Golden Ratio is given by the series
𝜑 =
13
8
+ ∑
(−1) 𝑛+1
(2𝑛 + 1)!
(𝑛 + 2)!𝑛! 42𝑛+3
∞
𝑛=0

6
The Golden Ratio is widely used from Renaissance artists of the 1500’s to modern
graphic designers as exemplified by the painting of Mona Lisa by Da Vinci to the logo design of
both Apple iPhone and Toyota. Now I know why the apple logo looks so nice and became
famous quickly. The Golden Ratio has a great influence on our everyday life without noticing. As
a conclusion, use the Golden Ratio to design your logo if you want to start a new business.
The Golden Rectangle shown in Fig 2 above was constructed by laying out Golden Ratio
rectangles, and then drawing the quarter-circle arcs in the square part of each rectangle.
Similarly a Golden Triangle may be drawn and appropriately divided and a spiral may also be
drawn as shown in Fig 3. The Golden Ladder is similar to the Golden Rectangle and the Golden
Triangle. I am going to introduce this new Euclidean geometric structure by applying the Golden
Ratio to the diameter of each adjacent circles. The structure is shown below in Fig 4, and I
called it the Golden Ladder.
Figure 2 Golden Rectangle Figure 3 Golden Triangle

7
I am goingto walkyouthroughthe processof constructionof a GoldenLadder.Draw two
circles,C1 withthe diameterd1= φ and C2 withthe diameterd2= φφ tangentto eachother.Addanother
circle C3 withthe diameterd3= φφ2
tangenttobothC1 and C2.Note that d1 > d2 > d3.The circlesC1,C2,
and C3 are mutuallytangent.Connectthe centersof the three circlestocreate a triangle.Thistriangle is
the firststepof the GoldenLadder.The fourthcircle C4 withthe diameterd4= φφ3
mustbe placed
tangentto bothC2 and C3.Againconnectthe centersof the circlesC2,C3, andC4 to get the second
triangle.Keepgoing.Eventuallyyouwill getasequence of circlesC1 ,C2,...,Cn,... withthe diametersd1,
d2,... , dn, ..., where dn= φφn-1
, and eachof the three circles Cn,Cn+1, Cn+2 are mutuallytangent.Youwill
alsoget a sequence of trianglesT1,T2,..., Tn,....Thissequence is calledthe GoldenLadder.
Figure 4 The Golden Ladder

8
2. Recursive Propertiesof the Golden Ladder
I want to introduce some recursive properties of the Golden Ladder. The first recursive
property is that all triangles in the Golden Ladder are similar triangle, the ratio between
corresponding sides of any triangle in the Golden Ladder and its next triangle is the Golden
Ratio (φ).
2.1 Theorem 1
1) All triangles in the Golden Ladder are similar.
2) The ratio of corresponding sides of triangles Tn and Tn+1 is the Golden Ratio φ.
Proof. Let the two triangles in figure 5 and 6 be Tn and Tn+1, which are taken from the
Golden Ladder. Triangle Tn was surrounded by three circles with diameters φn, φn+1 and φn+2,
triangle Tn+1 was surrounded by three circles with diameters φn+1, φn+2 and φn+3.
The three sides of Tn are Sn, Sn+1 and Sn+2, and the three sides of Tn+1 are Sn+2, Sn+3 and Sn+4. Both
triangles share the same side Sn+2 as we see in Fig 4 & 5. In order to prove this recursive
property, we need to prove the following:
Figure 6 n+1th
Triangle (Tn+1) in Golden LadderFigure 5 nth
Triangle (Tn) in Golden Ladder
Sn
Sn+1
Sn+2 Sn+2
Sn+3
Sn+4
Tn Tn+1

9
Table 1 Length of each side
Sn
Sn+2
=
Sn+1
Sn+3
=
Sn+2
Sn+4
= φ
The table above shows the length of each side, calculated using the diameter of the
circle. Now we can calculate Sn / Sn+2, Sn+1 / Sn+3 and Sn+2 / Sn+4.
Sn
Sn+2
=
(𝜙 𝑛 + 𝜙 𝑛+1 )/2
(𝜙 𝑛+1 + 𝜙 𝑛+2 )/2
=
(1 + 𝜙 )/2
(𝜙+ 𝜙2 )/2
=
1 + 𝜙
𝜙+ 𝜙2
=
1 + 𝜙
𝜙∗(1 + 𝜙)
=
1
𝜙
= 𝜑
Sn+1
Sn+3
=
(𝜙 𝑛 + 𝜙 𝑛+2 )/2
(𝜙 𝑛+1 + 𝜙 𝑛+3 )/2
=
(1 + 𝜙2 )/2
(𝜙+ 𝜙3 )/2
=
1 + 𝜙2
𝜙+ 𝜙3
=
1 + 𝜙2
𝜙∗(1 + 𝜙2)
=
1
𝜙
= 𝜑
Sn+2
Sn+4
=
(𝜙 𝑛+1 + 𝜙 𝑛+2 )/2
(𝜙 𝑛+2 + 𝜙 𝑛+3 )/2
=
(1 + 𝜙 )/2
(𝜙+ 𝜙2 )/2
=
1 + 𝜙
𝜙+ 𝜙2
=
1 + 𝜙
𝜙∗(1 + 𝜙)
=
1
𝜙
= 𝜑
Sn
Sn+2
= φ (1)
Thus, we proved the first recursive property.
Side Length
Sn (φn + φn+1 )/2
Sn+1 (φn + φn+2 )/2
Sn+2 (φn+1 + φn+2 )/2
Sn+3 (φn+1 + φn+3 )/2
Sn+4 (φn+2 + φn+3 )/2

10
The second recursive property is related to the area of the triangles. The ratio between
the area of any triangle in the Golden Ladder and its next triangle is the Golden Ratio square
(φ2).
2.2 Theorem 2
1) The ratio between the area of Tn and Tn+1 is φ2.
Proof. I will use figure 5 and figure 6 again for this proof. The area of Tn is An and the
area of Tn+1 is An+1. Let’s find the area of Tn and Tn+1 using Heron’s Formula, Pn represents the
perimeter.
Pn = (Sn + Sn+1 + Sn+2 )/2
An = √Pn ∗ (Pn − Sn) ∗ (Pn − Sn+1) ∗ (Pn − Sn+2 )
Pn+1 = (Sn+2 + Sn+3 + Sn+4 )/2
An+1 = √Pn+1 ∗ (Pn+1 − Sn+2) ∗ (Pn+1 − Sn+3) ∗ (Pn+1 − Sn+4 )
Next, we will divide An by An+1 to find the ratio:
An
An+1
=
√Pn ∗ (Pn − Sn) ∗ (Pn − Sn+1) ∗ (Pn − Sn+2 )
√Pn+1 ∗ (Pn+1 − Sn+2) ∗ (Pn+1 − Sn+3) ∗ (Pn+1 − Sn+4 )
An
An+1
= √
Pn
Pn+1
∗
(Pn − Sn)
(Pn+1 − Sn+2)
∗
(Pn − Sn+1)
(Pn+1 − Sn+3)
∗
(Pn − Sn+2 )
(Pn+1 − Sn+4 )

11
Next, we will be using equation (1) above for substitution to find the value of each term
above, including
Pn
Pn+1
,
(Pn− Sn)
(Pn+1− Sn+2)
,
(Pn− Sn+1)
(Pn+1− Sn+3)
, and
(Pn− Sn+2 )
(Pn+1− Sn+4 )
.
Pn
Pn+1
=
(Sn + Sn+1 + Sn+2 )/2
(Sn+2 + Sn+3 + Sn+4 )/2
=
φ ∗ Sn+2 + φ ∗ Sn+3 + φ ∗ Sn+4
Sn+2 + Sn+3 + Sn+4
=
𝜑 ∗ (Sn+2 + Sn+3 + Sn+4)
Sn+2 + Sn+3 + Sn+4
= 𝜑
(Pn − Sn)
(Pn+1 − Sn+2)
=
(Sn + Sn+1 + Sn+2 − Sn)/2
(Sn+2 + Sn+3 + Sn+4 − Sn+2)/2
=
Sn+1 + Sn+2
Sn+3 + Sn+4
=
φ ∗ Sn+3 + φ ∗ Sn+4
Sn+3 + Sn+4
=
𝜑 ∗ (Sn+3 + Sn+4)
Sn+3 + Sn+4
= 𝜑
(Pn− Sn+1)
(Pn+1− Sn+3)
and
(Pn− Sn+2 )
(Pn+1− Sn+4 )
are evaluated using a similar procedure to
(Pn− Sn)
(Pn+1− Sn+2)
above
which also equal to φ.
Now, we can substitution back to calculate the ratio between An and An+1,
An
An+1
= √ 𝜑 ∗ 𝜑 ∗ 𝜑 ∗ 𝜑
An
An+1
= 𝜑2 (2)

12
The third recursive property is also involves areas, but in this case the global area, the
sum of all triangle areas not the local area, will be used. The ratio between the area of any
triangle in the Golden Ladder and the total area of all triangles after this triangle is equal to the
Golden Ratio.
2.3 Theorem 3
1) The ratio between area of Tn and total area of Tn+1, Tn+2,…, Tm is the Golden Ratio φ as
m goes to infinite.
Proof. Our goal is to find the ratio below, where An is the area starting triangle and Am is
the area ending triangle as m goes to infinite for m > n:
𝐴 𝑛
𝐴 𝑛+1 + 𝐴 𝑛+2 + ⋯ + 𝐴 𝑚−1 + 𝐴 𝑚
Let’s starting by calculating the total area from Tn to Tm as m increases without limit.
An + An+1 + An+2 + ⋯ + Am-1 + Am
Next, let’s substitute all area using equation 2:
An + An /𝜑2
+ An /𝜑4
+ ⋯ + An /𝜑2(𝑚−1)
+ An /𝜑2𝑚
Let r = 1 / ϕ2, then the expression becomes:
An + An ∗ r + An ∗ r2
+ ⋯ + An ∗ r 𝑚−1
+ An ∗ r 𝑚
This is a geometric series and r < 1, so the total area becomes:

13
𝐴 𝑛 ∗
1
1 − 𝑟
Next let’s subtract An from the above expression, because we don’t want to include the
area of the first triangle:
𝐴 𝑛 ∗
1
1 − 𝑟
− 𝐴 𝑛
Then, we divide An by the expression above, the result is equivalent to the ratio we
wanted:
𝐴 𝑛
𝐴 𝑛∗
1
1−𝑟
−𝐴 𝑛
=
𝐴 𝑛
𝐴 𝑛+1+ 𝐴 𝑛+2+⋯+ 𝐴 𝑚−1+𝐴 𝑚
Let’s simplify the expression:
𝐴 𝑛
𝐴 𝑛 ∗
1
1 − 𝑟
− 𝐴 𝑛
=
𝐴 𝑛
𝐴 𝑛 ∗
1
1 − 𝑟
− 𝐴 𝑛 ∗
1 − 𝑟
1 − 𝑟
=
𝐴 𝑛
𝐴 𝑛 ∗
r
1 − 𝑟
=
1 − 𝑟
𝑟
Finally, we substitute the definition of r into the result:
1 − 𝑟
𝑟
=
1 −
1
𝜑2
1
𝜑2
= 𝜑2
− 1 = 𝜑
𝐴 𝑛
∑ 𝐴𝑖
𝑚
𝑖=𝑛+1
= 𝜑 (3)

14
3. More about the Golden Ladder
3.1 Spiral in the Golden Ladder
There is another version of the Golden Ladder. From the Golden Ladder in figure 4, flip
all triangles into its pervious triangle starting at the second triangle. The result Golden Ladder is
shown in figure 7. In this version, it’s possible to draw a spiral that connect the center of all
tangent circles which is similar to the Golden Rectangle.
Figure 7 embedded Golden Ladder

15
3.2 Find the End Point of the Golden Ladder
In figure 8, three line can be drawn in the Golden Ladder to find the end point. The first
line would be drawing a straight line that passes through the intersections of every two
adjacent circles. The second line is also a straight line, which is tangent to all circles that on the
top portion of the Golden Ladder. And the third line is similar to the second line, but in this
case, it will be tangent to all circles on the bottom portion of the Golden Ladder. The
intersection of these three lines would be the end point, which is where the circles are
approaching to in the Golden Ladder.
Figure 8 End point of the Golden Ladder

16
3.3 The Golden Ladderin Three Dimension
The Golden Ladder may be presented in three dimension by applying the Golden Ratio
to the diameters of tangent spheres. I am calling it the Golden Tower (figure 9). This idea of
dimensional increase suggests that it is possible to extend the concept to the nth dimension
after completing some research on the three dimensional case. Instead of finding the ratio
between the areas of triangles, the ratio between the volumes of the tetrahedron would be our
interest. A tetrahedron can be constructed by connecting the centers of any four consecutive
spheres.
Figure 9 The Golden Tower

17
4. A “Processing”Simulation of the Golden Ladder
4.1 How the Program Works?
Processing is a java based virtual design programming language, which is a free software
that provides a great environment to simulate simple 2D and 3D objects. Drawing tangent
circles is very easy in real life, but to calculate the center of the next tangent circle with precise
diameter would not be as easy as you think. The program was written based on the math
showing below.
Figure 10 processing sketch

18
In the processing sketch, start with the two tangent circles. In order to find the center of
the next circle, we will need to setup two distances. Let the center of the first circle be X1, Y1,
and the distance from the first circle to the third circle be D1. For the second circle, the center
be X2, Y2, distance be D2. The unknown would be the center of the third center X3, Y3. We will
setup and solve equations below before writing the program.
√(𝑋3 − 𝑋1)2 + (𝑌3− 𝑌1)2 = 𝐷1 (4)
√( 𝑋3 − 𝑋2)2 + ( 𝑌3− 𝑌2)2 = 𝐷2 (5)
Two unknowns and two equations, very simply, right? You can try to solve it or think
about it before I show you my approach. My procedure would surprise you and involves solving
a quadratic equation. This makes sense because quadratic equations can have two solutions
and there are two possible circles that can be tangent to the two pervious circles.
1. Square both sides of equation 4 and 5, and find the difference between them.
( 𝑋3 − 𝑋2)2
+ ( 𝑌3 − 𝑌2)2
− ( 𝑋3 − 𝑋1)2
− (𝑌3 − 𝑌1)2
= 𝐷22
− 𝐷12
2. By a little simplification, we obtain the equation below,
2( 𝑋1 − 𝑋2) 𝑋3 + 2( 𝑌1 − 𝑌2) 𝑌3 = 𝐷22
− 𝐷12
− 𝑋22
− 𝑌22
− 𝑋12
− 𝑌12
3. Denote by temp =
𝐷22
−𝐷12
−𝑋22
−𝑌22
−𝑋12
−𝑌12
2
, simplify, and the expression becomes:
( 𝑋1 − 𝑋2) 𝑋3 + ( 𝑌1− 𝑌2) 𝑌3 = 𝑡𝑒𝑚𝑝

19
Solving for X3 gives us,
𝑋3 =
𝑡𝑒𝑚𝑝 − ( 𝑌1− 𝑌2) 𝑌3
( 𝑋1 − 𝑋2)
Now substitute X3 into equation 4,
√(
𝑡𝑒𝑚𝑝 − ( 𝑌1 − 𝑌2) 𝑌3
( 𝑋1 − 𝑋2)
− 𝑋1)
2
+ ( 𝑌3 − 𝑌1)2 = 𝐷1
4. Square the equation above and transform it to a standard quadratic equation a(Y3)2 +
b(Y3) + c = 0. Solve the quadratic equation and substitute each of the two values of Y3 into
equations (4) or (5). That would give us two corresponding X3 values. Below is snippet of code
showing the calculation of the quadratic coefficient a, b and c.
float a = pow( (y1 - y2), 2) / pow( ( x1 - x2), 2) + 1;
float b = -2 * (y1 - y2) * temp / pow ( ( x1 - x2), 2) - 2 * y1 + 2 * x1 * (y1 - y2) / (x1 - x2);
float c = pow( temp, 2) / pow ( (x1 - x2), 2) + pow(x1, 2) + pow(y1, 2) - pow(distance1, 2) - 2 * x1
* temp / (x1 - x2);
The above process would repeat for each tangent circle. The program runs very well,
that mean the math approach is one correct way to solve the problem, I am sure there is a way
to solve this problem much easier.
4.2 Program Output
There are two modes you can select after you start the program. Mode 1 is for the
Golden Ladder and Mode 2 is for embedded Golden Ladder.

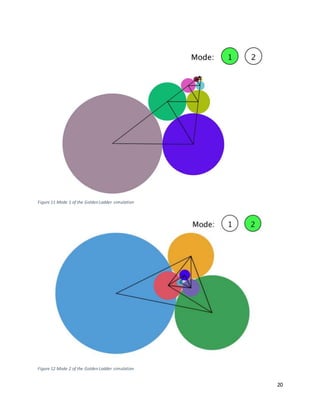
20
Figure 11 Mode 1 of the Golden Ladder simulation
Figure 12 Mode 2 of the Golden Ladder simulation

21
4.3 How to Use this Program
You can drag the Golden Ladder with your mouse, and rotate it by pressing the
rotation icon. Press space to add circle to the Golden Ladder, and press ‘b’ on your
keyboard to remove circle from the Golden Ladder. Avoid to delete circle while there
are two circles left. Press 1 or 2 to switch mode. Press the ‘up arrow’ key to zoom in and
the ‘down arrow’ key to zoom out.
4.4 Why Writingthis Program?
From this program, we can find out the exact location or the center of each
circle. These new data of the Golden Ladder would give us more understanding of the
structure and its properties. Also these information would be helpful for solving future
problem.
5. Results
In this work, a new Euclidean structure the Golden Ladder is introduced. Three recursive
properties have been proven, which relative to the area and circumference of triangles within
the Golden Ladder. And this structure has been expanded to the three dimension. More
properties have been found and will be proven in the near future.

22
6. References
[1] Alberto, Fiorenza. Giovanni, Vincenzi. From Fibonacci Sequence to the Golden Ratio. Journal
of Mathematics Hindawi Publishing Corporation(2013).
[2] Pamela, M. Pallett. Stephen, Link. Kang, Lee. New “golden” ratios for facial beauty. Vision
Research 50 (2010) 149-154.
[3]. “Debunking The Myth Of Apple’s ‘Golden Ratio’ ”. fastcodesign.com. Mark, Wilson. June 4,
2013.
[4] “Golden Ratio”. mathworld.wolfram.com. Eric, Weisstein. May 4, 2015.
[5] "Golden Ratio in Geometry." http://www.cut-the-
knot.org/do_you_know/GoldenRatio.shtml. Bogomolny, A. n.d.
[6] Boyer, C. B. History of Mathematics. New York: Wiley, p. 56, 1968.
[7] Brown, D. The Da Vinci Code. New York: Doubleday, 2003.
[8] Coxeter, H. S. M. “The Golden Section, Phyllotais, and Whythoff’s Game.” Scripta
Mathematica 19, 135-143, 1953.
[9] Martin Ohm. Die Reine Elementar-Mathematik. 1835.

23
7. Appendix
The program consists of two classes Circle and Triangle other than the main code.
Circle class
class Circle
{
float x, y, d, r, g, b;
Circle(float x, float y, float d, color r, color g, color b)
{
this.x = x;
this.y = y;
this.d = d;
this.r = r;
this.g = g;
this.b = b;
}
void display()
{
fill(r, g, b);
noStroke();
ellipse(x, y, d, d);
}
}
Triangle class

24
class Triangle
{
float x1, y1, x2, y2, x3, y3;
Triangle(float x1, float y1, float x2, float y2, float x3, float y3)
{
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.x3 = x3;
this.y3 = y3;
}
void display()
{
stroke(0);
line(x1, y1, x2, y2);
line(x2, y2, x3, y3);
line(x1, y1, x3, y3);
}
}
Main code
ArrayList<Circle> Circles = new ArrayList<Circle>();

25
ArrayList<Triangle> Triangles = new ArrayList<Triangle>();
ArrayList<Circle> Circles2 = new ArrayList<Circle>();
ArrayList<Triangle> Triangles2 = new ArrayList<Triangle>();
float phi = 1.618034;
float phi2 = phi - 1;
float tempPhi = phi * phi2;
float tempPhi2 = tempPhi;
float ratio;
int biggerCircle = 0, smallerCircle = 1;
int biggerCircle2 = 0, smallerCircle2 = 1;
boolean press = false;
float px, py, tranX, tranY, rotateAngle = 0;
PImage rotate1, rotate2;
float rotate2X, rotate2Y, rotate1X, rotate1Y;
float zoom = 1;
int mode = 1;
float mode1X, mode1Y, mode2X, mode2Y;
float count1 = 0, count2 = 0;
void setup()
{
size(displayWidth - 50, displayHeight - 100);
smooth();

26
textSize(30);
textAlign(CENTER, CENTER);
rotate1 = loadImage("rotate1.png");
rotate2 = loadImage("rotate2.png");
rotate2X = width/20;
rotate2Y = height*9/10;
rotate1X = width/7;
rotate1Y = height*9/10;
mode1X = width*8.8/10;
mode1Y = height/10;
mode2X = width*9.5/10;
mode2Y = height/10;
ratio = 150;
Circles.add(new Circle(phi * ratio, phi * ratio, phi * ratio * 2, (int)random(255),
(int)random(255), (int)random(255)));
Circles.add(new Circle(phi * ratio + ratio, (tempPhi + phi * 2) * ratio - ratio/5, tempPhi * ratio *
2, (int)random(255), (int)random(255), (int)random(255)));
Circles2.add(new Circle(phi * ratio, phi * ratio, phi * ratio * 2, (int)random(255),
Circles2.add(new Circle(phi * ratio + ratio, (tempPhi + phi * 2) * ratio - ratio/5, tempPhi * ratio
* 2, (int)random(255), (int)random(255), (int)random(255)));
}

27
void draw()
{
background(255);
image(rotate2, rotate2X, rotate2Y);
image(rotate1, rotate1X, rotate1Y);
imageMode(CENTER);
stroke(0);
strokeWeight(2);
fill(0);
text("Mode:", width*4/5, height/10);
if(mode == 1)
{
fill(65, 247, 78);
}
else
{
fill(255);
}
ellipse(width*8.8/10, height/10, width/20, width/20);
fill(0);
text("1", width*8.8/10, height/10);
if(mode == 2)

28
{
fill(65, 247, 78);
}
else
{
fill(255);
}
ellipse(width*9.5/10, height/10, width/20, width/20);
fill(0);
text("2", width*9.5/10, height/10);
scale(zoom);
if(press)
{
tranX = mouseX - px;
tranY = mouseY - py;
}
translate(tranX, tranY);
if(mousePressed)
{
if(dist(mouseX, mouseY, rotate2X, rotate2Y) < 50)
{
rotateAngle -= 0.01;

29
}
if(dist(mouseX, mouseY, rotate1X, rotate1Y) < 50)
{
rotateAngle += 0.01;
}
}
rotate(rotateAngle);
translate(-phi * ratio, -phi * ratio);
if(mode == 1)
{
for(int i = 0; i < Circles.size(); i++)
{
Circles.get(i).display();
}
for(int i = 0; i < Triangles.size(); i++)
{
Triangles.get(i).display();
}
}
else
{
for(int i = 0; i < Circles2.size(); i++)
{

30
Circles2.get(i).display();
}
for(int i = 0; i < Triangles2.size(); i++)
{
Triangles2.get(i).display();
}
}
}
void keyPressed()
{
if(key == ' ')
{
if(mode == 1)
{
count1++;
float d1 = Circles.get(biggerCircle).d;
float d2 = Circles.get(smallerCircle).d;
float d3 = d2 * phi2;
float distance1 = (d1 + d3)/2;
float x1 = Circles.get(biggerCircle).x;
float x2 = Circles.get(smallerCircle).x;
float y1 = Circles.get(biggerCircle).y;
float y2 = Circles.get(smallerCircle).y;

31
float temp = pow(distance2, 2) - pow(distance1, 2);
temp = temp + pow(x1, 2) - pow(x2, 2) + pow(y1, 2) - pow(y2, 2);
temp = temp / 2;
float b = -2 * (y1 - y2) * temp / pow( ( x1 - x2), 2) - 2 * y1 + 2 * x1 * (y1 - y2) / (x1 - x2);
float c = pow( temp, 2) / pow ( (x1 - x2), 2) + pow(x1, 2) + pow(y1, 2) - pow(distance1, 2) - 2 *
x1 * temp / (x1 - x2);
float yRoot1 = ( -b + sqrt( pow(b, 2) - 4 * a * c) ) / (2 * a);
float yRoot2 = ( -b - sqrt( pow(b, 2) - 4 * a * c) ) / (2 * a);
float xRoot1, xRoot2;
if(count1%2 == 1){
xRoot1 = -sqrt( pow(distance2, 2) - pow( (yRoot1 - y2), 2)) + x2;
xRoot2 = sqrt( pow(distance2, 2) - pow( (yRoot2 - y2), 2)) + x2;
}
else
{
}

32
float realRootY, realRootX;
if( (yRoot1 + xRoot1) > (yRoot2 + xRoot2))
{
realRootY = yRoot1;
realRootX = xRoot1;
}
else
{
realRootY = yRoot2;
realRootX = xRoot2;
}
tempPhi = tempPhi * phi2;
Circles.add(new Circle(realRootX, realRootY, tempPhi * ratio * 2, (int)random(255),
Triangles.add(new Triangle(x1, y1, x2, y2, realRootX, realRootY));
println("root1: " + xRoot1 + ", " + yRoot1);

33
biggerCircle += 1;
smallerCircle += 1;
}
}
if(key == ' ')
{
if(mode == 2)
{
count2++;
float d1 = Circles2.get(biggerCircle2).d;
float d2 = Circles2.get(smallerCircle2).d;
float d3 = d2 * phi2;
float x1 = Circles2.get(biggerCircle2).x;
float x2 = Circles2.get(smallerCircle2).x;
float y1 = Circles2.get(biggerCircle2).y;
float y2 = Circles2.get(smallerCircle2).y;
float temp = pow(distance2, 2) - pow(distance1, 2);
temp = temp + pow(x1, 2) - pow(x2, 2) + pow(y1, 2) - pow(y2, 2);
temp = temp / 2;

34
float b = -2 * (y1 - y2) * temp / pow( ( x1 - x2), 2) - 2 * y1 + 2 * x1 * (y1 - y2) / (x1 - x2);
float c = pow( temp, 2) / pow ( (x1 - x2), 2) + pow(x1, 2) + pow(y1, 2) - pow(distance1, 2) - 2 *
x1 * temp / (x1 - x2);
float yRoot1 = ( -b + sqrt( pow(b, 2) - 4 * a * c) ) / (2 * a);
float yRoot2 = ( -b - sqrt( pow(b, 2) - 4 * a * c) ) / (2 * a);
float xRoot1, xRoot2;
if(count2%3 == 1){
}
else
{
}
tempPhi2 = tempPhi2 * phi2;
if(count2%3 == 0)
{

35
Circles2.add(new Circle(xRoot1, yRoot1, tempPhi2 * ratio * 2, (int)random(255),
Triangles2.add(new Triangle(x1, y1, x2, y2, xRoot1, yRoot1));
}
else
{
Circles2.add(new Circle(xRoot2, yRoot2, tempPhi2 * ratio * 2, (int)random(255),
Triangles2.add(new Triangle(x1, y1, x2, y2, xRoot2, yRoot2));
}
biggerCircle2 += 1;
smallerCircle2 += 1;
}
}
if(key == 'b')
{
if(mode == 1)

36
{
count1--;
biggerCircle -= 1;
smallerCircle -= 1;
tempPhi = tempPhi / phi2;
Circles.remove(Circles.get(Circles.size() - 1));
Triangles.remove(Triangles.get(Triangles.size() - 1));
}
else
{
count2--;
biggerCircle2 -= 1;
smallerCircle2 -= 1;
tempPhi2 = tempPhi2 / phi2;
Circles2.remove(Circles2.get(Circles2.size() - 1));
Triangles2.remove(Triangles2.get(Triangles2.size() - 1));
}
}
if(key == CODED)
{
if(keyCode == UP)
{
zoom += 0.2;
}

37
else if(keyCode == DOWN)
{
zoom -=0.2;
}
}
}
void mousePressed()
{
press = true;
px = mouseX - tranX;
py = mouseY - tranY;
println(mouseX + " " + mouseY);
if(dist(mouseX, mouseY, mode1X, mode1Y) < width/20)
{
mode = 1;
}
else if(dist(mouseX, mouseY, mode2X, mode2Y) < width/20)
{
mode = 2;
}
}
void mouseReleased()
{
press = false;

The Golden Ladder

More Related Content

What's hot

Viewers also liked

Similar to The Golden Ladder

The Golden Ladder