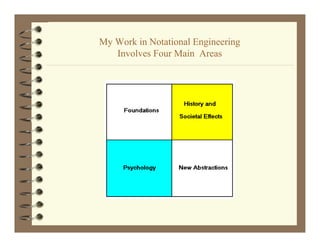
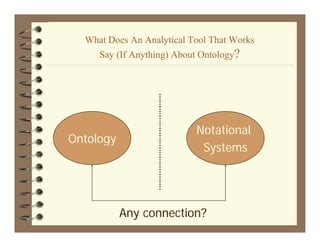
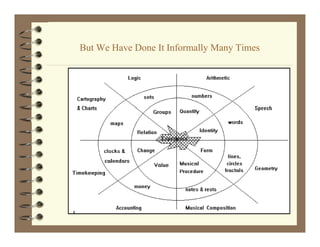
The document discusses a talk by Jeffrey G. Long on the evolution of abstractions, exploring the nature and significance of notational systems and proposing a new metaphysical framework for understanding them. The presentation critiques existing definitions of abstraction and outlines a plan for enhancing the processes involved in developing notational systems, suggesting the establishment of a new field called 'notational engineering.' Long emphasizes the historical journey of abstraction and the complexity of settling new abstraction spaces while advocating for improved communication amongst researchers in the field.

1. Cover Page
The Evolution of
Abstractions
Author: Jeffrey G. Long (jefflong@aol.com)
Date: September 11, 1997
Forum: Talk presented at a luncheon meeting of the Washington Evolutionary
Systems Society.
Contents
Page 1: Proposal
Pages 2‐22: Slides (but no text) for presentation
License
This work is licensed under the Creative Commons Attribution‐NonCommercial
3.0 Unported License. To view a copy of this license, visit
http://creativecommons.org/licenses/by‐nc/3.0/ or send a letter to Creative
Commons, 444 Castro Street, Suite 900, Mountain View, California, 94041, USA.
Uploaded June 22, 2011

2. Title: The Evolution of Abstractions
Speaker: Jeff Long, Director, GWU Notational Engineering Laboratory
Date: September 11, 1997 at Noon
Location: Faculty Club, The George Washington University (call ahead for
lunch reservations please!)
What is it that gives notational systems their power? Are they merely
convenient collections of arbitrary tokens and rules that just happen to
have a useful application in the real world? Or might there be a deeper
connection between notational systems and reality?
This talk will explore this question, and answer in the affirmative. We
will discuss the conventional definitions of "abstraction" and their
inadequacies, and seek a new definition. To do this we will sketch a
theoretical framework -- a metaphysical system that attempts to account
for the the law-abiding nature of physical objects, the nature of laws,
and, ultimately, the nature of abstractions.
The talk will discuss the notion of an "abstraction space" such as the
field of numbers, and how three such spaces historically have been
explored and tokenized ("settled"). The talk will end with a brief
outline of a plan for improving the abstraction space settlement process.
This plan is essentially an agenda for the proposed new field of
"notational engineering".

3. The Evolution of Abstractions
Jeffrey G. Long
GWU Notational Engineering Laboratory
Copyright 1997 © Jeffrey G. Long

4. My Work in Notational Engineering
y g g
Involves Four Main Areas

5. What Does An Analytical Tool That Works
Say (If Anything) About Ontology?
Notational
Ontology
Systems
Any connection?

6. Sections of this Talk
S ti f thi T lk
1. The hi i l process of exploring abstractions
h historical f l i b i
2. An alternative metaphysical system
3.
3 A general strategy for improving the correlation process

7. Part One
The Historical Process of Exploring Abstractions

8. There A M
Th Are Many Definitions of ‘Abstractions’
D fi iti f ‘Ab t ti ’
 Anything not concrete or physically perceivable (love,
hi h i ll i bl (l
nations)
 Ideal/perfect forms in the noumenal world (perfect justice,
justice
perfect sphere)
 Ideas or classifications formed by mental separation from
particulars (rules, sets)
 Entities lacking causal powers (universals, numbers, ideas)
 Referents of words that are not proper nouns (dogs, cats)
(dogs
These have not been very useful distinctions
– they conflate things that must be distinguished

9. AT
Taxonomy of Ab t ti
f Abstractions
 Tokens & Operators
 Expressions composed of tokens, generated by operators
 Expressions referred to by other expressions
 Entities, classes & ideas named by expressions
 Expressions further delimited by their position in statements
 Variables acting as position-holders within statements
 Ruleforms composed of ordered sets of variables
 Particular laws/rules are the resolution of ruleforms

10. Exploring N Ab t ti S
E l i a New Abstraction Space Is Very Diffi lt
I V Difficult
 Requires exploring and mapping into useful tokens and
i l i d i i f l k d
syntax
 By definition entity was never before imagined
definition,
(discoverer seems nuts)
 There is no predefined language available for the concepts
involved
 Users require training and practice to “see” the entities
(literacy)

11. Settling “Q tit S
S ttli “Quantity Space” Required Centuries
”R i dC t i
 Tallies: 30,000 BP
lli
 Accounting tokens: 8,000 BC
 Whole numbers: 1,900 BC
1 900
 Rational numbers: 500 BC
 Zero and real numbers: 200
 Complex (imaginary) numbers: 1545
 Transfinite numbers: c. 1900

12. Settling “F
S ttli “Form Space” Required Centuries
S ”R i dC t i
 Euclidean geometry: c. 325 BC
lid
 Non-Euclidean (hyperbolic, elliptic) geometries: c. 1850
 Fractal geometry: c. 1975
c

13. Settling “Id tit S
S ttli “Identity Space” Required Centuries
”R i dC t i
 Speech: 100,000 BP?
h
 Pictograms: 3,400 BC
 Ideograms: 2,200 BC
2 200
– Syllabic writing: 3,000 BC
– Consonantal alphabet: 1,500 BC
– Full alphabet: c. 776 BC
 Stroke: 1969

14. But W H
B t We Have Done It Informally Many Times
D I f ll M Ti

15. Part Two
An Alternative Metaphysical System
for Exploring the Basic Issues

16. The P
Th Prevailing (Materialist) Paradigm
ili (M t i li t) P di
 Universe consists solely of matter/energy (physicalism)
 This substance follows certain laws, sought by science
 The universe is becoming more uniform over time (2nd Law)
 These laws and all such abstractions are useful fictions
(nominalism)
( i li )
 Metaphysical questions are pseudo-questions (positivism)
But this paradigm leaves unanswered many questions viewed as
non-scientific
– why is the universe lawful?
– what are laws/rules, really? Do they have component parts?

17. An Alternative (Ultra-Structural) Paradigm
A Alt ti (Ult St t l) P di
 The material world doesn’t follow laws, it is l
h i l ld d f ll l i laws
– We perceive and define entities according to the laws they happen
to follow
 A natural law is an ordered set of noumenal abstractions
– e.g. identity & group & form, form&quantity & state
 ‘L
‘Laws’ are the name we give to the interaction of
’ th i t th i t ti f
noumenal abstractions
 Interaction of rules produces processes which generate
p p g
“events”
– what we perceive to be the material world
– eventually these include mental abstractions
t ll th i l d t l b t ti
 Noumenal abstractions become more complex over time
– they operate on themselves and evolve

18. Examples of Noumenal Abstractions
E l fN l Ab t ti
 Possible Identity
ibl d i
 Possible Group
 Possible Relation
 Possible Form
 Possible Quantity
 Possible State

19. This I li C t i F t
Thi Implies Certain Features of Noumenal Abstractions
fN l Ab t ti
 Each i a fundamentally different type of entity
h is f d ll diff f i
– Each has unique types of possible relations with other noumenal
abstractions
– One cannot be fully translated into another
 They are self-referential
 Th are combinable or able to have interactions
They bi bl bl t h i t ti
 We can perceive them only by mind
– Similar to how we learn to perceive physical objects
 They exist independently of any mind

20. Part Three
h
A General Strategy for
Improving the Correlation Process

21. Study R l ti
St d Revolutionary Notational Systems
N t ti l S t
 Discovery of new noumenal abstractions
i f l b i
– quantities, sets, infinitessimals, value, form, relation
 Progressive exploration of noumenal abstractions
– imaginary numbers, fractal geometry, fuzzy sets
 Improved praxis with better tokens, media and teaching
– Leibniz versus Newton’s tokenization, printing versus hand-
lettering, writing versus oral tradition

22. Develop Complete List of
p p
Current and Potential Noumenal Abstractions
 Identify all current notational systems (20+)
d if ll i l ( )
 Determine uniqueness, i.e. inter-translatability (6+)
 Is there any pattern, a la Mendeleev? (probably not!)
pattern
 Are there practical and/or logical limitations for each
noumenal abstraction?

23. Improve Communication Among
p g
Notational Researchers
 Define scope, nature, basic concepts of subject
fi b i f bj
 Identify sources of information/participants
– people (maybe 1% of each group using a NS)
– books, articles, Web sites (esp. foreign language)
 Establish clearinghouse
– Internet discussions (notation listserver)
– conferences (NOTATE’97 at SSA)
– publications
p

24. Conclusion
C l i
 Alternative paradigm can be tested by its utility
l i di b db i ili
– an effective mental abstraction says something about noumenal
abstractions
 Broaden the “linguistic turn” to be a “notational turn”
– metaphysics is important after all
– limitations are not just those of language, but all NS
language
– language is not the only tool or reference point
 We can speed up the process of settling abstractions
– make it more of a regular discipline than an ad hoc event