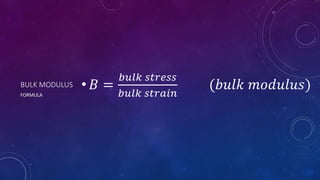The document discusses the bulk modulus, a numerical constant that describes the elastic properties of materials under uniform pressure, and explains how it measures a substance's resistance to volume changes. It provides formulas for calculating bulk modulus and compressibility and illustrates a practical application involving a hydraulic press with oil under increased pressure. The example demonstrates how to compute the decrease in volume using both bulk modulus and compressibility concepts.

1. BULK STRESS
HTTPS://YOUTU.BE/4WLL5AX9MM4

2. BULK MODULUS
• Bulk modulus, a numerical constant that
describes the elastic properties of
a solid or fluid when it is under pressure on all
surfaces. The applied pressure reduces the
volume of a material, which returns to its
original volume when the pressure is removed.
Sometimes referred to as the incompressibility,
the bulk modulus is a measure of the ability of
a substance to withstand changes in volume
when under compression on all sides. It is
equal to the quotient of the applied pressure
divided by the relative deformation.
definition

3. BULK MODULUS • 𝐵 =
𝑏𝑢𝑙𝑘 𝑠𝑡𝑟𝑒𝑠𝑠
𝑏𝑢𝑙𝑘 𝑠𝑡𝑟𝑎𝑖𝑛
(𝑏𝑢𝑙𝑘 𝑚𝑜𝑑𝑢𝑙𝑢𝑠)
FORMULA

4. BULK STRAIN
• Is the amount of deformation
brought by the change in pressure
definition

5. BULK STRAIN
•𝑏𝑢𝑙𝑘 𝑣𝑜𝑙𝑢𝑚𝑒 𝑠𝑡𝑟𝑎𝑖𝑛 =
∆𝑉
𝑉𝑜
formula

6. BULK MODULUS
𝐵 =
𝑏𝑢𝑙𝑘 𝑠𝑡𝑟𝑒𝑠𝑠
𝑏𝑢𝑙𝑘 𝑠𝑡𝑟𝑎𝑖𝑛
= −
∆𝑝
∆𝑉/𝑉
𝑜
(𝑏𝑢𝑙𝑘 𝑚𝑜𝑑𝑢𝑙𝑢𝑠)
General formula
𝑠𝑡𝑟𝑒𝑠𝑠 =
𝐹⊥
𝐴
= 𝑝 = 𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒
∆𝑠𝑡𝑟𝑒𝑠𝑠 = ∆𝑝

7. BULK MODULUS
Compressibility is a measure of the relative
volume change of a solid or a fluid in response
to a pressure change.
The inverse of bulk modulus is called
compressibility.

8. BULK MODULUS
𝑘 =
1
𝐵
= −
∆𝑉
𝑉
𝑜
∆𝑝
= −
1
𝑉
𝑜
∙
∆𝑉
∆𝑝
(𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑏𝑖𝑙𝑖𝑡𝑦)
The inverse of bulk modulus is called
compressibility.

9. BULK MODULUS
A hydraulic press contains 0.25𝑚3
(250L) of oil.
Find the decrease in volume when it is subjected to
an increase in pressure ∆𝑝 = 1.6 × 102
𝑃𝑎 (about
160atm or 2300psi). The bulk modulus of the oil is
𝐵 = 5.0 × 109
𝑃𝑎 (about 5.0 × 104
𝑎𝑡𝑚), and its
compressibility is 𝑘 =
1
𝐵
= 20 × 10−6
𝑎𝑡𝑚−1
.
Problem solving

10. BULK MODULUS
• We need to find the decrease in volume ∆𝑉 .
Identifying the target

11. BULK MODULUS
• What do we have in hand?
• ∆𝑝 = 1.6 × 102
𝑃𝑎
• 𝐵 = 5.0 × 109
𝑃𝑎
• 𝑘 =
1
𝐵
= 20 × 10−6
𝑎𝑡𝑚−1
.
• 𝑉
𝑜 = 0.25𝑚3
(250L)
data

12. BULK MODULUS •Execute
•We derive a formula for ∆𝑉.
•
𝐵∆𝑉
𝑉𝑜
= −
∆𝑝
1
•∆𝑉 = −
∆𝑝
1
𝑉𝑜
𝐵
solution

13. BULK MODULUS
• ∆𝑉 = −
1.6×102𝑃𝑎
1
0.25𝑚3
5.0×109𝑃𝑎
= −8.0 × 10−4
𝑚3
𝑜𝑟 − .80𝐿
• Alternatively we can use the concept of compressibility
which will give us,
• 𝑘 =
1
𝐵
= −
∆𝑉
𝑉𝑜
∆𝑝
= −
1
𝑉𝑜
∙
∆𝑉
∆𝑝
• So ∆𝑉 = −𝑘𝑉
𝑜∆𝑝
• ∆𝑉 = −𝑘𝑉
𝑜∆𝑝
• ∆𝑉 = − 20 × 10−6
𝑎𝑡𝑚−1
0.25𝑚3
1.6 × 102
𝑃𝑎 =
− 8.0 × 10−4
𝑚3
𝑜𝑟 − .80𝐿
solution