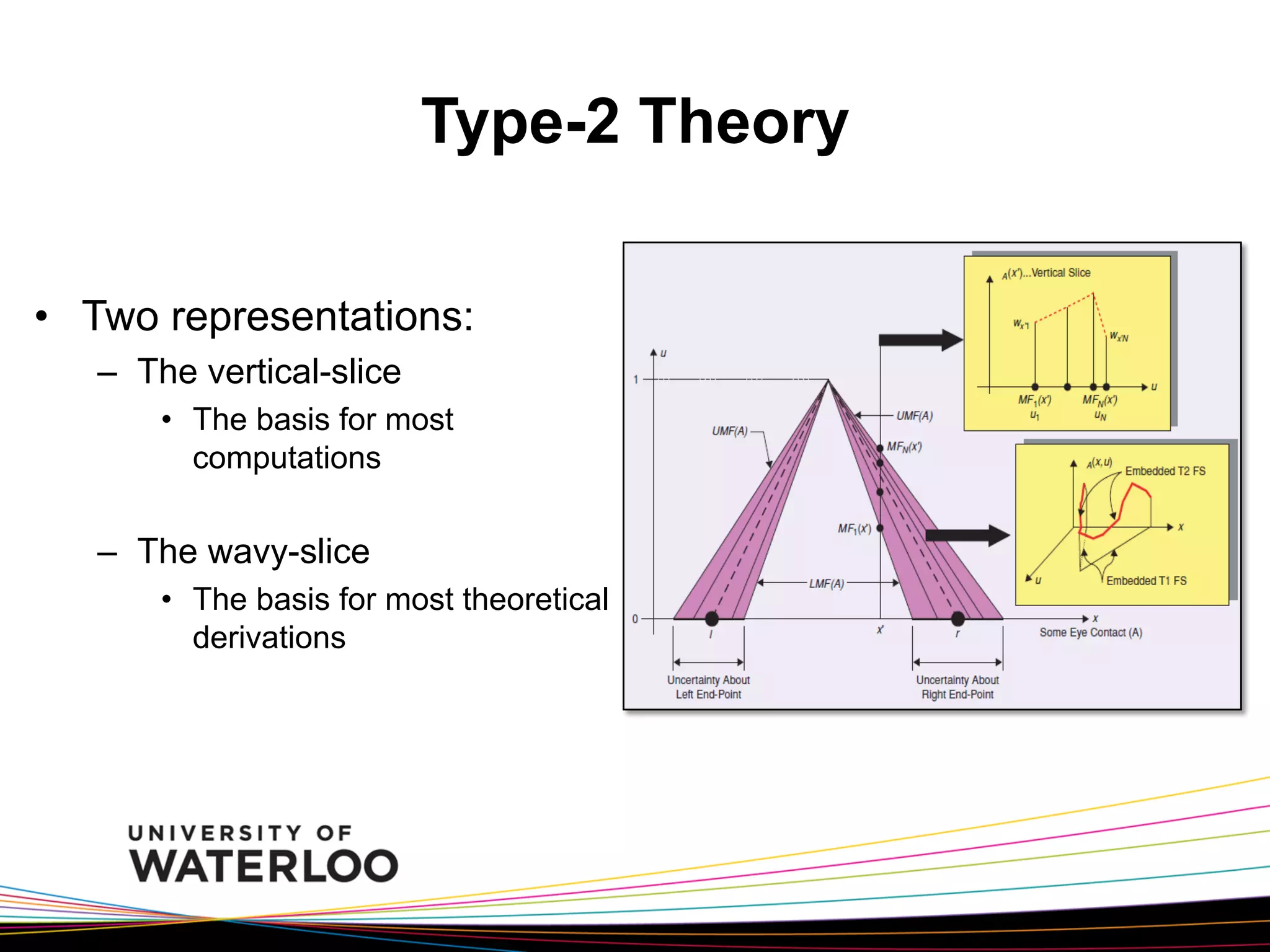
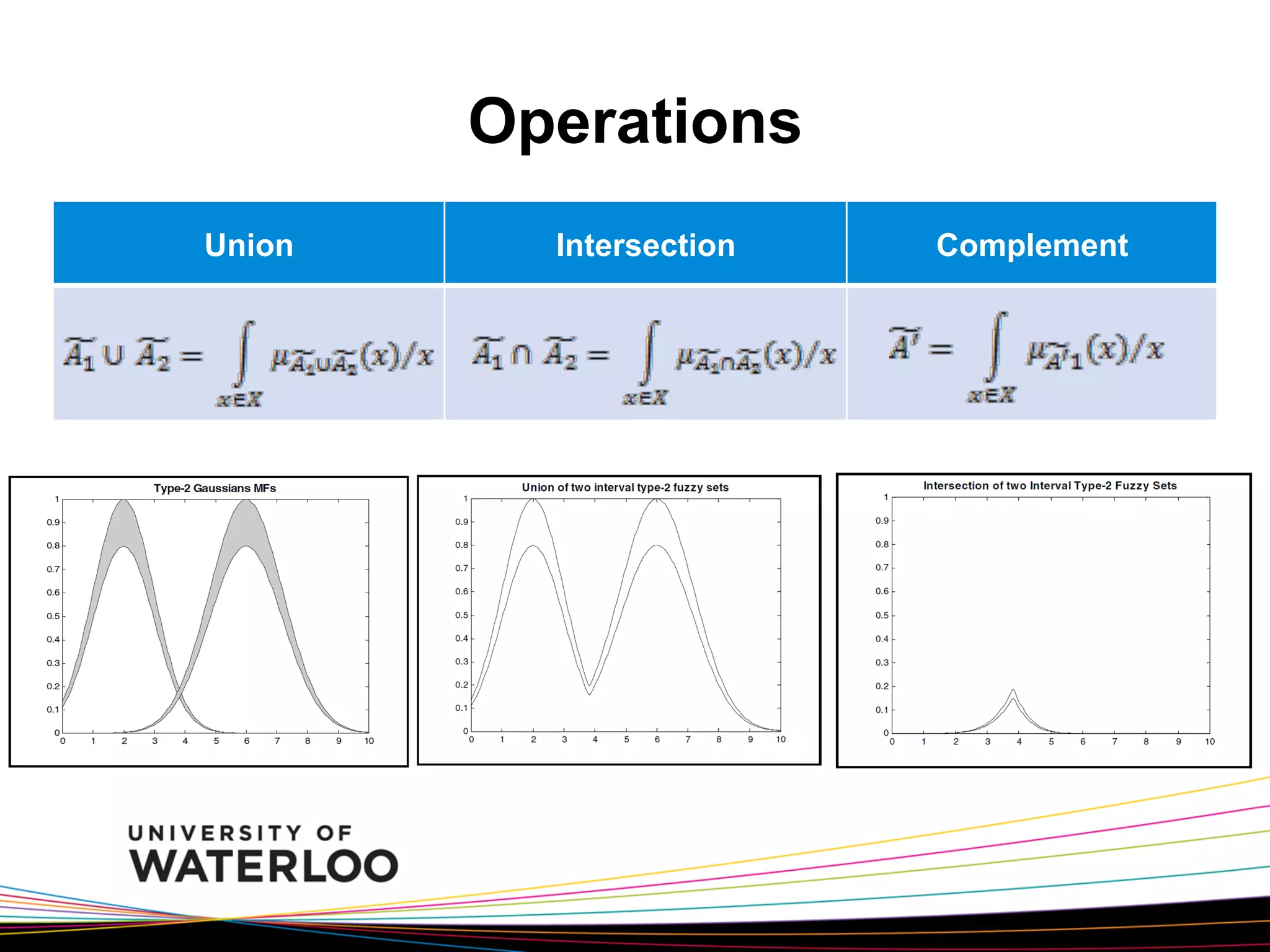
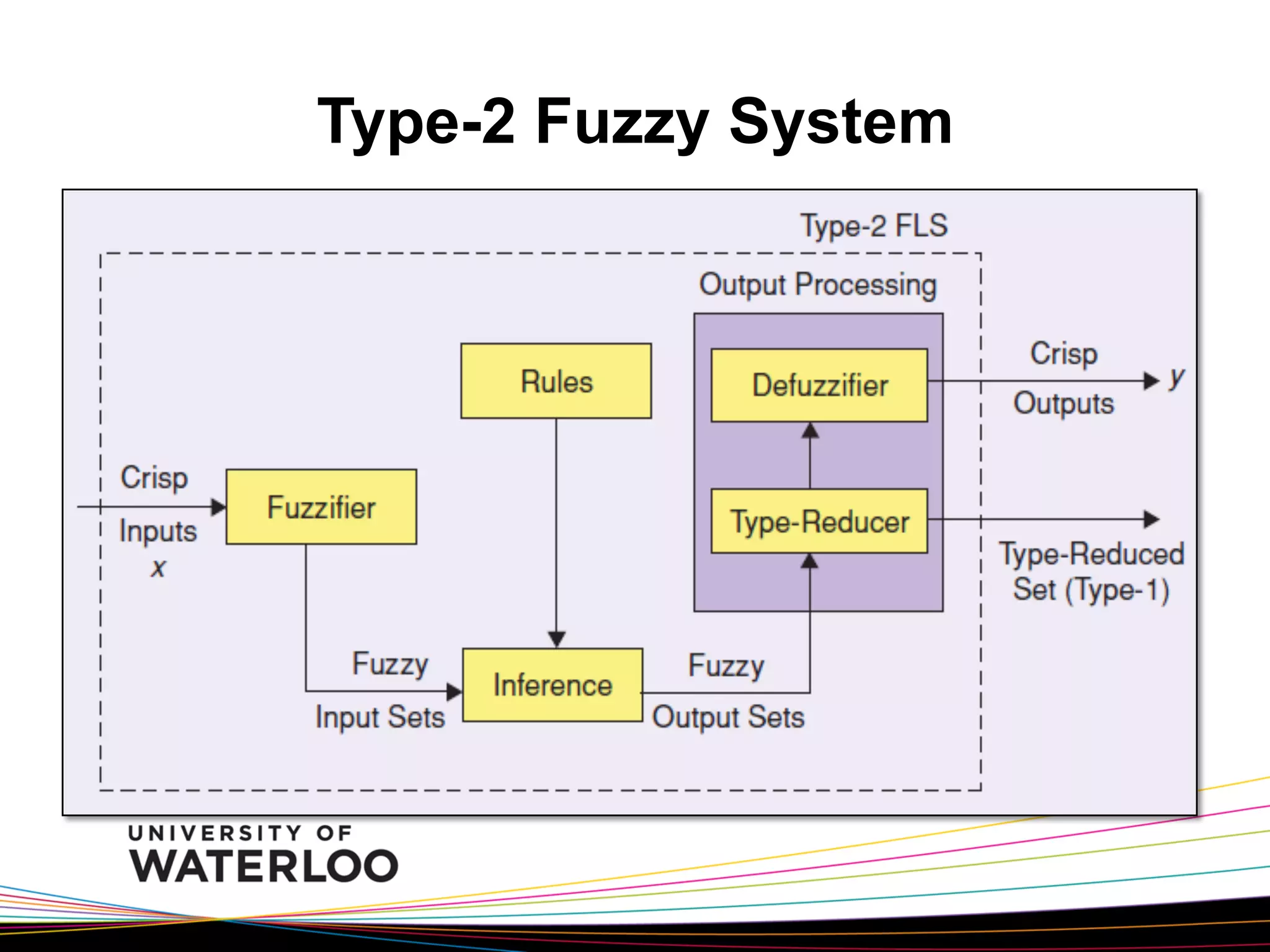
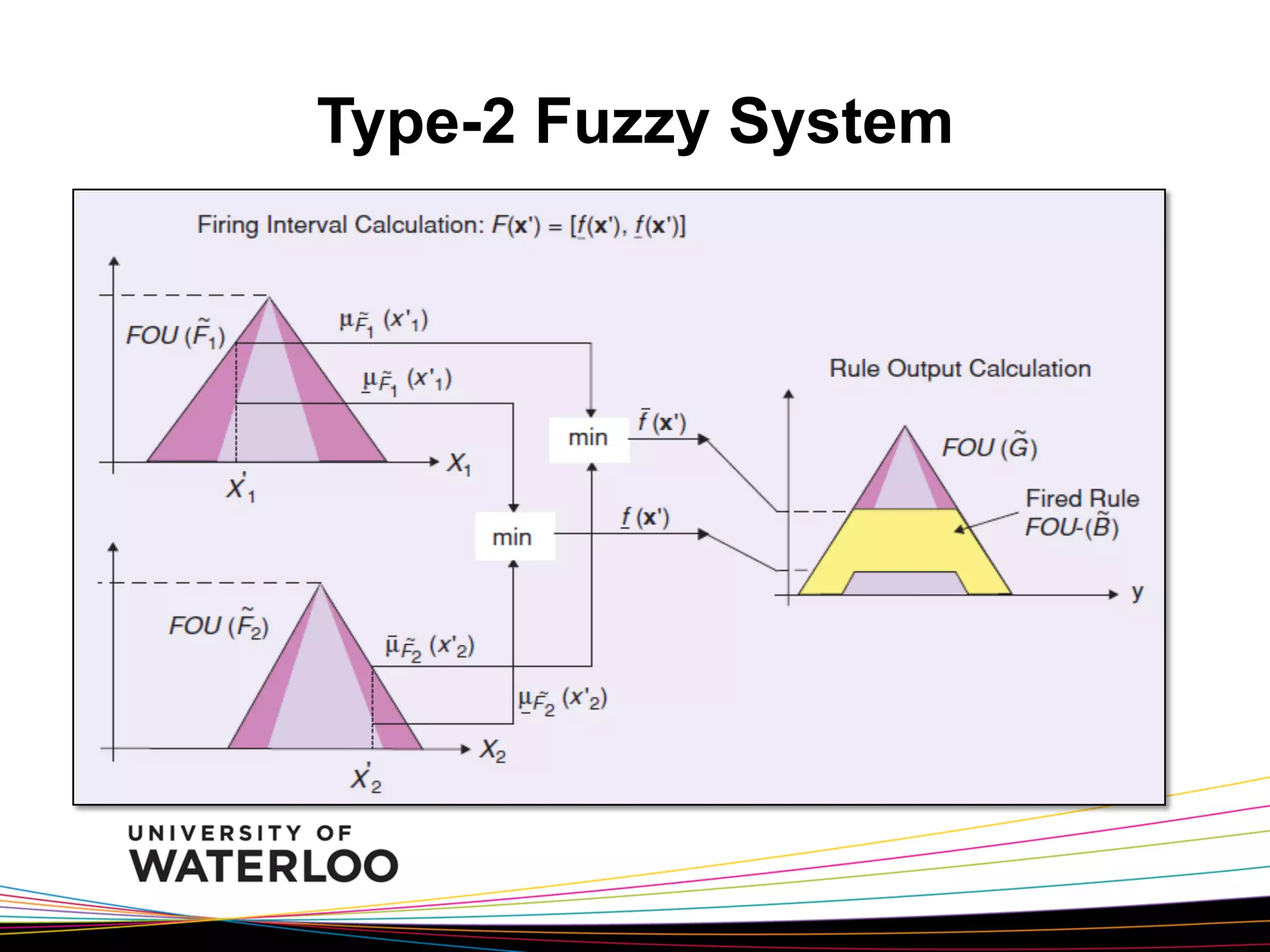
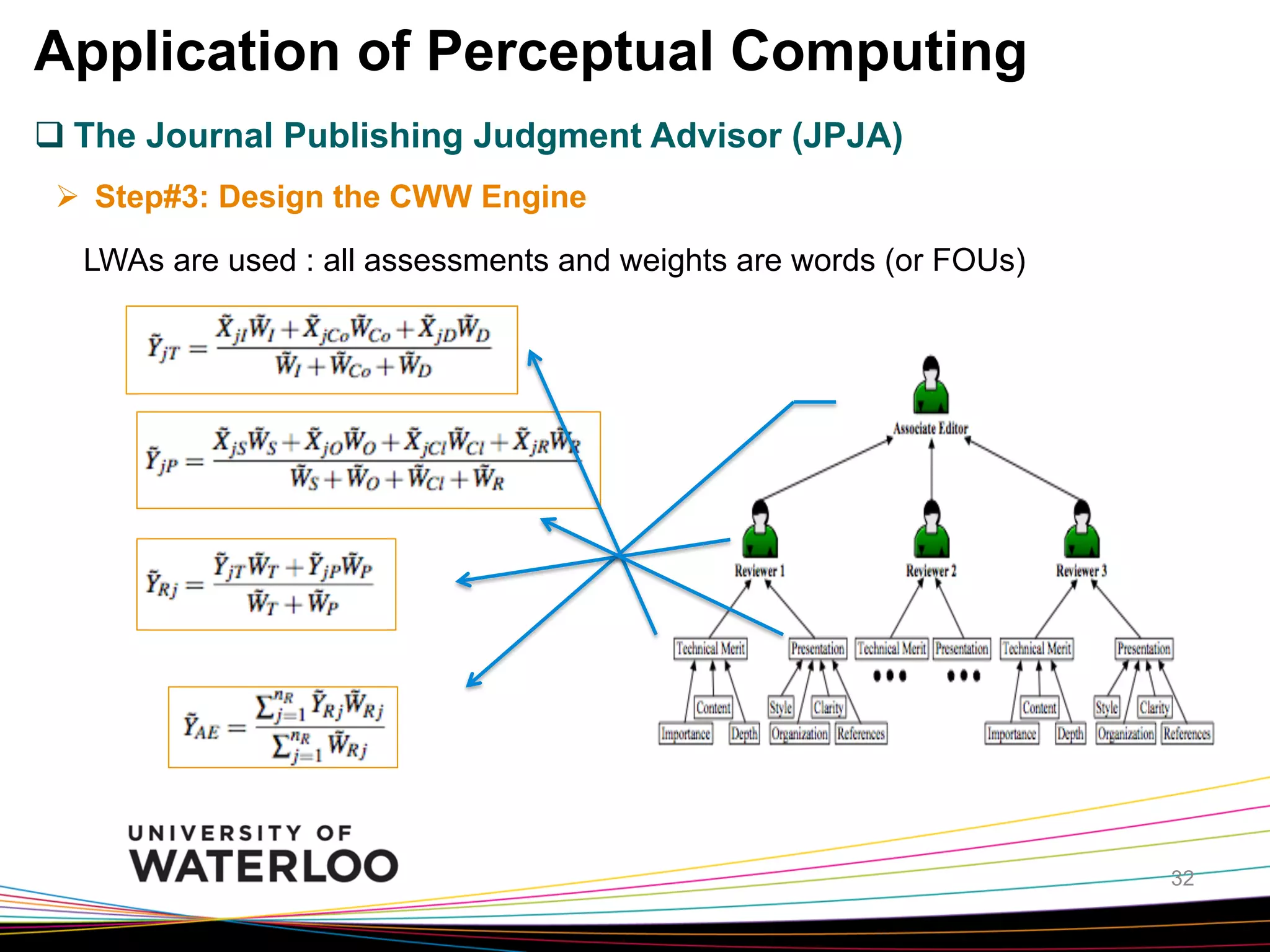
The document introduces type-2 fuzzy sets, which can model uncertainty, and their applications in perceptual computing. It discusses interval and general type-2 fuzzy sets, type-2 fuzzy set theory and operations, type-2 fuzzy systems, and an example of using type-2 fuzzy logic for image edge detection. It then explains computing with words, perceptual computing using type-2 fuzzy logic to model linguistic uncertainty, and presents an example application of a journal publishing judgment advisor that uses perceptual computing.

1. Fuzzy Set Type-2
Theory, Applications and Examples
Mahmoud Alish
Noha El-Prince
Nouf Al Alawi

2. Agenda
•
Introduction to type-2 fuzzy set.
o Interval Type-2 & General Type-2
o Type-2 Terminologies
•
Type-2 fuzzy set Theory & Systems
o Theory & operation
o Inference System
o Example (Image Edge Detection)
•
Application (Computing With Words)
o
o
o
o
o
Computing with Words (CWW)
Perceptual Computing (Per-C)
Example of Per-C: Journal Publishing Judgment Advisor (JPJA)
Analysis of Per-C
Conclusion

3. Introduction
• Introduced by Zadeh as theoretical concept in 1975 to
handles the uncertainty that Type-1 cannot handle.
• Three sources of uncertainties
– The meanings of the words used in the antecedents & consequents
• words mean different things to different people
– The noise associated with Measurements of activating in the fuzzy
system.
– The noise associated with data that are used to tune the parameters
in the fuzzy system.

4. Introduction
• Able to model and minimize the effects of uncertainties in the
fuzzy logic systems.
• The grades of membership are fuzzy not crisp like Type-1
– Called a “fuzzy-fuzzy set.”
• Fuzzy set of type-2 denoted by ( )
• If all uncertainty disappears è Type-2 reduces to a Type-1

5. Interval & General
Type-2 Fuzzy Set
• The membership function is three-dimensional (model
uncertainty).
–
–
–
–
More difficult to use and understand.
Third dimension difficult to draw.
Not easy to collect simple well-defined terms for the third dimension
The use of type-2 is computationally more complicated.
• There are two types of fuzzy set type-2
– General Type-2 Fuzzy Set
– Interval Type-2 Fuzzy set

6. Interval & General
Type-2 Fuzzy Set
General Type-2
• Primary Membership (2D Domain)
• Secondary Membership (3D
Domain)
IntervalType-2
• The third dimension value is
constant everywhere è ignored

7. The Terminologies
• FOU: Footprint of uncertainty.
• UMF & LMF: Upper and lower membership functions

8. Agenda
•
Introduction to type-2 fuzzy set.
o Interval Type-2 & General Type-2
o Type-2 Terminologies
•
Type-2 fuzzy set Theory & Systems
o Theory & operation
o Inference System
o Example (Image Edge Detection)
•
Application (Computing With Words)
o
o
o
o
o
Computing with Words (CWW)
Perceptual Computing (Per-C)
Example of Per-C: Journal Publishing Judgment Advisor (JPJA)
Analysis of Per-C
Conclusion

9. Type-2 Theory
• Two representations:
– The vertical-slice
• The basis for most
computations
– The wavy-slice
• The basis for most theoretical
derivations

10. Type-2 Theory
• Both representations called
covering theorems
– Union of all vertical slices
– Union of all embedded Type-1 that
cover the entire FOU.
• known as the Mendel-John
Representation Theorem (RT)

11. Operations
Union
Intersection
Complement

12. Type-2 Fuzzy System

13. Type-2 Fuzzy System

14. Type-2 Fuzzy System
• Singleton Type-2 Fuzzy Logic Systems
– Based on Mandani
– Uncertainties in the antecedents or consequents
• Non-singleton Fuzzy Logic Systems
– Based on Mandani
– Uncertainties in both the antecedents, consequents and input
measurement
– More complicated.
• Sugeno Type-2 Fuzzy Systems
– Based on Takagi and Sugeno

15. The Use of Interval Type-2 Fuzzy Logic as a
Method for Edge Detection using Gaussian as MF
• Detecting the edges allows feature extraction & construction of input
vectors for neural networks with aims of image recognition
• Traditional Methods
– The gradient methods like Roberts, Prewitt and Sobel for detect edges.
• Looking for maximum and minimum in first derived
– The Laplacian methods like Marrs-Hildreth
• Finding the zeros of second derived

16. The Use of Interval Type-2 Fuzzy Logic as a
Method for Edge Detection using Gaussian as MF
Inputs
DH:
Derivative
Horizontal
DV:
Derivative
Vertical
HP:
high-pass
filter
M:
low-pass
filter
Inputs equation
Rules
If (DH is LOW) and (DV is LOW) then (EDGES
is LOW)
If (DH is MEDIUM) and (DV is MEDIUM) then
(EDGES is HIGH)
If (DH is HIGH) and (DV is HIGH) then
(EDGES is HIGH)
If (DH is MEDIUM) and (HP is LOW) then
(EDGES is HIGH)
If (DV is MEDIUM) and (HP is LOW) then
(EDGES is HIGH)
If (M is LOW) and (DV is MEDIUM) then
(EDGES is LOW)
If (M is LOW) and (DH is MEDIUM) then
(EDGES is LOW)

17. The Use of Interval Type-2 Fuzzy Logic as a
Method for Edge Detection using Gaussian as MF

18. The Use of Interval Type-2 Fuzzy Logic as a
Method for Edge Detection using Gaussian as MF
•
By using Type-2 fuzzy more than
half of the pixels were cleared
without depreciating the image
– reduce in drastic form the cost of
training in a neural network.

19. Agenda
•
Introduction to type-2 fuzzy set.
o Interval Type-2 & General Type-2
o Type-2 Terminologies
•
Type-2 fuzzy set Theory & Systems
o Theory & operation
o Inference System
o Example (Image Edge Detection)
•
Application (Computing With Words)
o
o
o
o
o
Computing with Words (CWW)
Perceptual Computing (Per-C)
Example of Per-C: Journal Publishing Judgment Advisor (JPJA)
Analysis of Per-C
Conclusion

20. Computing with Words (CWW)
CWW
is
:
“A
methodology
in
which
words
are
used
in
place
of
numbers
for
compu7ng
and
reasoning..”
(Zadeh, 1996- Ref[4])
Distance
=
500
Ann
lives
near
Mary
Example:
consider
the
proposi<ons:
p1
=
Ann
lives
near
Mary
p2
=
Mary
lives
near
Clara.
Query
:
“How
far
is
Ann
from
Clara?,”
Answer:
Ann
lives
not
far
from
Clara.
Fig. Compute with numbers vs.
compute with words
20

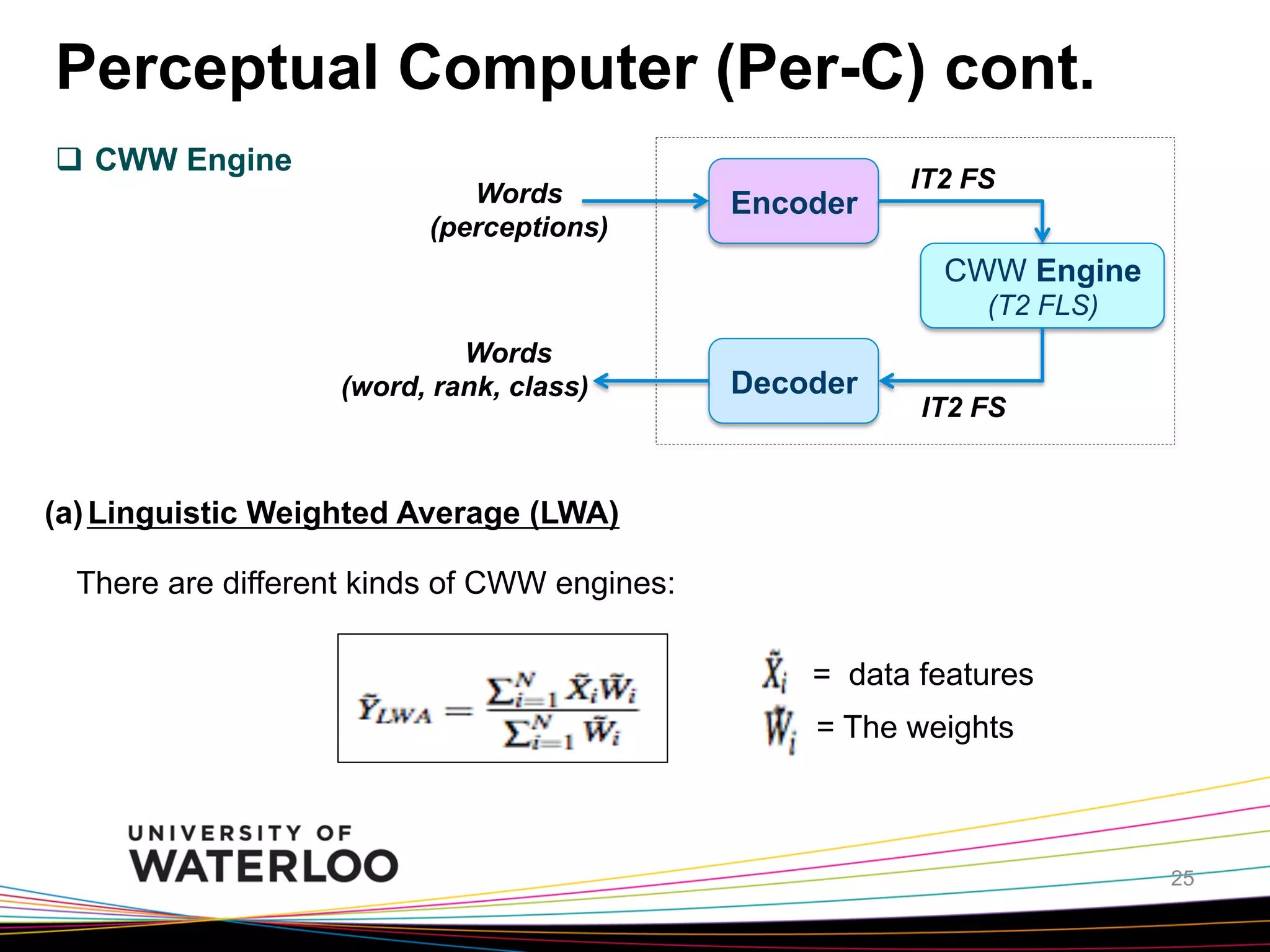
21. Perceptual Computer (Per-C)
Words
(perceptions)
Encoder
IT2 FS
CWW Engine
(T2 FLS)
Words
(word, rank, class)
Decoder
IT2 FS
Fig. Architecture of a Per-C (Mendel Ref[5],2002)
•
•
•
Words mean different things to different People = uncertainty in words = FL
Uncertainty a person has about the meaning of a word (intra-personal
uncertainty)=> T1 FL
Uncertainties that a group of people have about the meaning of the word
(inter-personal uncertainty) => T2 FL
[Ref 6]
21

22. Perceptual Computer (Per-C) cont.
Encoder:
Encoding
Words --------------- > IT2 FSs (Code Book = Words + their FOUs)
Approach
q Encoding Approaches:
Ø Person FOU
Ø Interval End-points
Ø IA Approach (mostly practically used)
22

23. Perceptual Computer (Per-C) cont.
q IA Approach:
(1) Collect interval end point data for a word
from a group of persons.
(2) After removing outliers, intervals
are classified as either : interior, leftshoulder, right-shoulder IT1FS.
(3) Each word’s data intervals is mapped
into its respective T1 interior, left
shoulder or right shoulder MF
(4) Interpret the MFs as an embedded
T1 FS. Using Representation
theorem and take their union.
(5) Result is a FOU for an IT2FS model of
the word.
(6) The words + their FOUs constitute a
codebook.
23

24. Perceptual Computer (Per-C) cont.
v Code Book Sample:
v FOUs of 4 words
24

25. Perceptual Computer (Per-C) cont.
q CWW Engine
Words
(perceptions)
Encoder
IT2 FS
CWW Engine
(T2 FLS)
Words
(word, rank, class)
Decoder
IT2 FS
(a) Linguistic Weighted Average (LWA)
There are different kinds of CWW engines:
= data features
= The weights
25

26. Perceptual Computer (Per-C) cont.
q CWW Engine
(b) Perceptual Reasoning (PR)
Given : A rule base with K rules, each of the form:
Where
new input
and
are words modeled by IT2 FSs
(j = 1,...,p) are also words modeled by IT2 FSs
=
Output:
where
Firing level
of Rk
Jaccard similarity
for IT2 FSs
and
are upper and lower MFs of
26

27. Perceptual Computer (Per-C) cont.
q Decoder
• Three Types of decoders
according to three types
of recommendations:
Words
(perceptions)
IT2 FS
CWW Engine
(T2 FLS)
Words
(word, rank, class)
Recomm.
Type
Encoder
Decoder
IT2 FS
Decoder Type
Word
Similarity is calculated between the CWW o/p and all the words in
the codebook. The o/p is the word with max. similarity.
Rank
A centroid-based ranking method for IT2 FSs can be used to
select the best alternative.
Class
A decision category is the o/p made by a classifier
e.g. Average subsethood
27

28. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
28

29. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
Ø Step#1: Modify Paper review form
29

30. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
Ø Step#2: Design the Encoder
I. Codebook for the reviewer
Two code books are needed :
( words (used by the reviewer), weights )
Fig. FOUs for the five-word Sub-codebook R1
Fig. FOUs for the three-word Sub-codebook R2
30

31. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
Ø Step#2: Design the Encoder – cont.
II. Codebook for the weights
Weights correspond to Importance (W Ĩ ),
Content (W Co) and Depth (W D).
̃
̃
Fig. FOUs for the three-word Sub-codebook W1
Weights correspond to Weights correspond
to Style (W ̃S), Organization (W O), Clarity
̃
(W ̃Cl) and Reference (W R).
̃
Fig. FOUs for the four-word Sub-codebook W2
Weights correspond to Weights correspond
to Weights correspond to Technical Merit
(W ̃T ) and Presentation ( W P ) .
̃
Fig. FOUs for the two-word Sub-codebook W3
31

32. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
Ø Step#3: Design the CWW Engine
LWAs are used : all assessments and weights are words (or FOUs)
32

33. Application of Perceptual Computing
q The Journal Publishing Judgment Advisor (JPJA)
Ø Step#4: Design the decoder
• The decoder for the JPJA is a classifier: it classifies the overall paper quality
into 3 classes: Accept, Rewrite, or reject.
• A decoding codebook is needed to store the FOUs for these 3 words.
• 2 approaches for constructing such a codebook:
a.) using a survey (used in JPJA)
b.) using training examples.
• O/p:
33

34. Analysis of Per-C
q Advantages
o Very good tool for hierarchal decision making.
o Diverse i/ps can be aggregated across different hierarchies
o Uncertainties associated with these i/p s are preserved and
propagate into the final evaluation.
q Limitations
o Not data adaptive
o Inputs (Interval end points) needs human interaction.
34

35. Conclusion
• Type-2 fuzzy set enables us to model the effect of uncertainty in (FLS)
better than Type-1 fuzzy set as it combines uncertainty about the
membership function into fuzzy set theory.
• Type-2 fuzzy set is used when there is uncertainty about the
membership grades or difficult to determine the membership
functions of fuzzy logic system.
• Per-C is a very useful tool for hierarchal and distributed decision making
and has great potential in solving complex decision-making problems.
35

36. Questions ?

37. References
•
[1] Oscar Castillo and Patricia Melin. Type-2 Fuzzy Logic: Theory and Applications. 223, 2008
Springer-Verlag Berlin Heidelberg. July 2007.
•
[2] Jerry M. Mendel and Robert I. Bob John. Type-2 Fuzzy Sets Made Simple. IEEE
TRANSACTIONS ON FUZZY SYSTEMS, VOL. 10, NO. 2, APRIL 2002.
•
[3] Jerry M Mendel. Type-2 fuzzy sets and system: an overview. IEEE computational intelligent
magazine, vol 2, no. 1, pp. 20-29. February 2007.
•
[4] L.A. Zadeh, Fuzzy logic = computing with words, IEEE Trans. on Fuzzy Systems 4 (1996)
103-111.
•
[5] J.M. Mendel, An architecture for making judgments using computing with words, Int. J. Appl.
Math. Comput. Sci. 12 (3) (2002) 325–335.
•
[6] J.M.Mendel, Perceptual Computing, Willey, 2010.
37