Uploaded byVikram Seervi
Subject-1 Engineering Mathematics GATE Questions.pdf
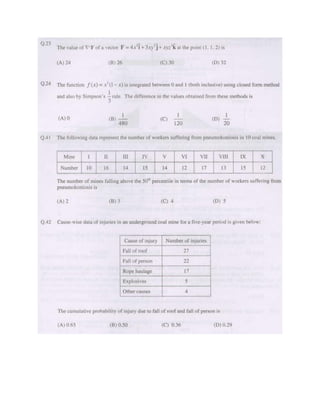
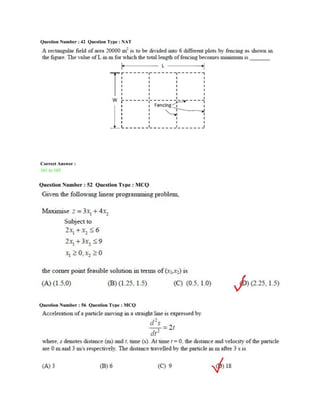
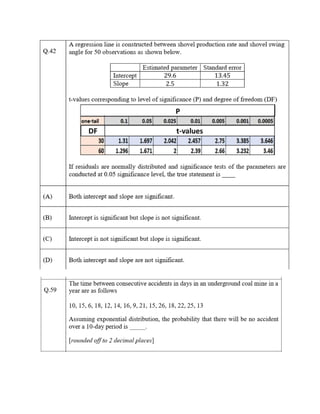
The document outlines the GATE syllabus for Engineering Mathematics from 2007 to 2024, detailing key topics such as linear algebra, calculus, vector calculus, differential equations, probability, statistics, and numerical methods. It is compiled by Dr. Vikram Seervi, an assistant professor in Mining Engineering at CTAE, Udaipur. The document serves as a comprehensive resource for students preparing for the GATE exam.
More Related Content
Similar to Subject-1 Engineering Mathematics GATE Questions.pdf
Subject-1 Engineering Mathematics GATE Questions.pdf
- 1. GATE – MiningEngineering (Subject Wise Questions 2007-2024) Subject: 1-Engineering Mathematics Syllabus for GATE 2024 Section 1: Engineering Mathematics Linear Algebra: Matrices and Determinants; Inverse and Rank of matrix; Systems of linear equations; Eigen values and Eigen vectors. Cayley-Hamilton Theorem. Calculus: Limit, continuity and differentiability; Partial Derivatives; Mean value theorems; Indeterminate forms and L’ Hospital’s rule; Maxima and minima; Taylor’s theorem; Sequences and series; Test for convergence; Fourier series. Vector Calculus: Gradient; Divergence and Curl; Line; surface and volume integrals; Stokes, Gauss and Green’s theorems. Differential Equations: Linear and non-linear first order ODEs; Higher order linear ODEs with constant coefficients; Cauchy’s and Euler’s equations. Probability and Statistics: Measures of central tendency and dispersion; hypothesis testing; Binomial, Poisson, exponential and normal distributions; Correlation and regression analysis. Numerical Methods: Solutions of linear algebraic equations; Interpolation; Integration of trapezoidal and Simpson’s rule; Single and multi-step methods for differential equations. Compiled by: Dr. Vikram Seervi (IIT-BHU, Varanasi) Assistant Professor, Department of Mining Engineering, College of Technology and Engineering (CTAE), Udaipur Email: vikramseervi007@gmail.com https://www.ctae.ac.in/singlePage.php?id=57&type=DP
- 2.
- 4.
- 7.
- 9.
- 11.
- 12.
- 14.
- 16.
- 17.
- 21.
- 22.
- 24.
- 25.
- 28.
- 29.
- 31.
- 35.
- 38.
- 43.