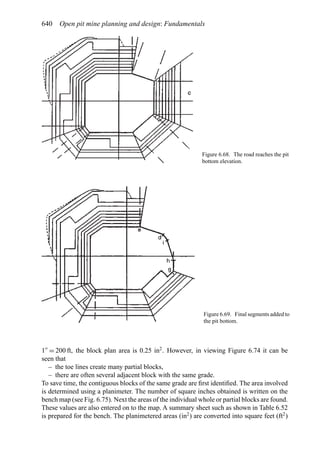
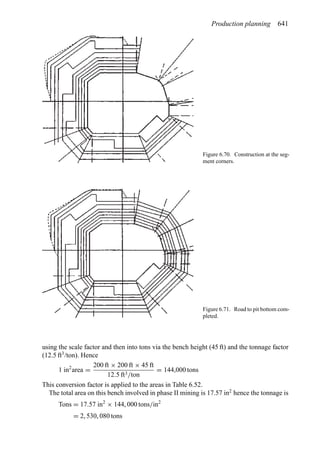
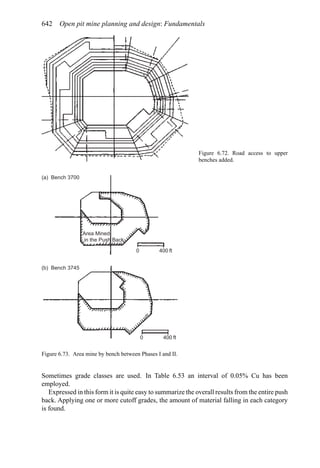
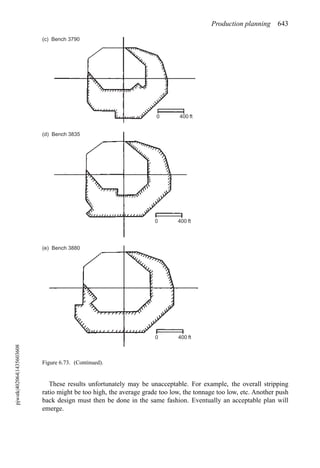
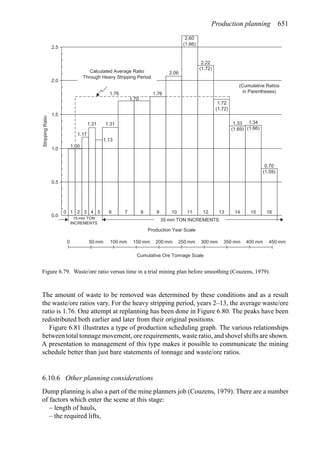
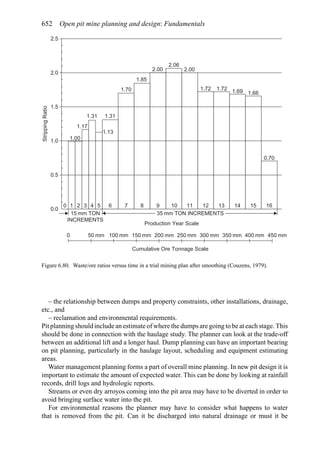
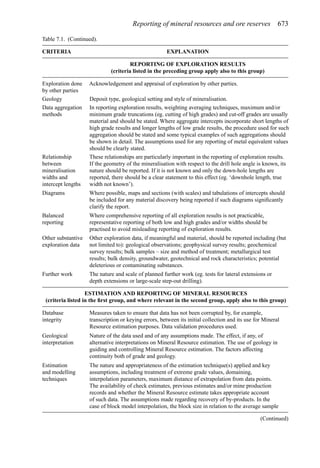
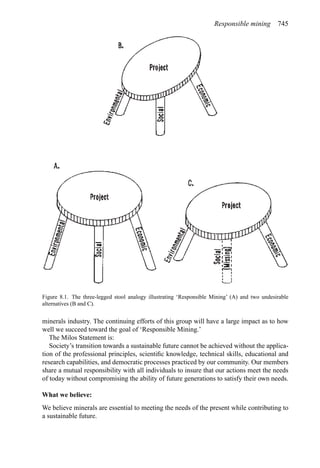
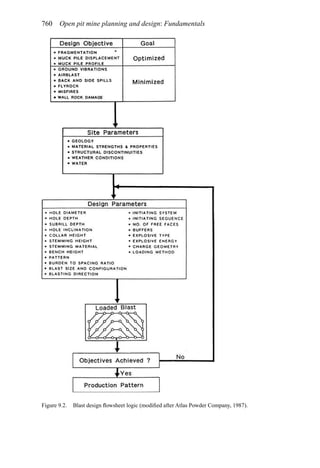
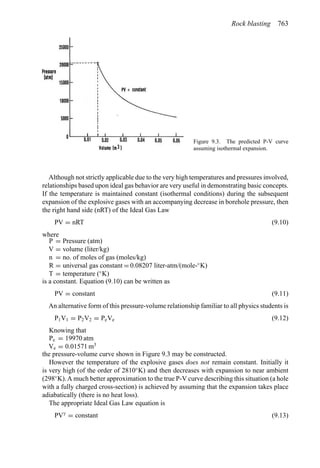
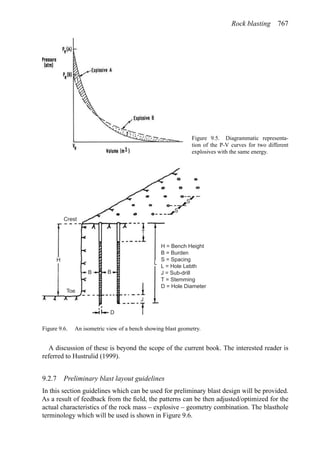
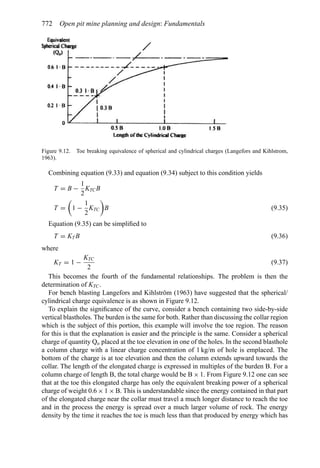
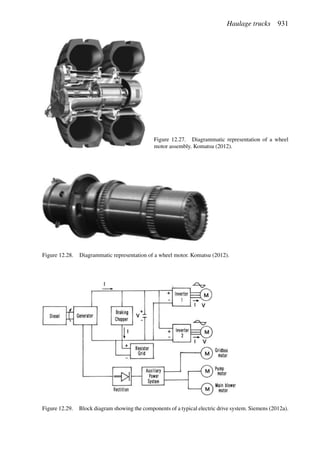
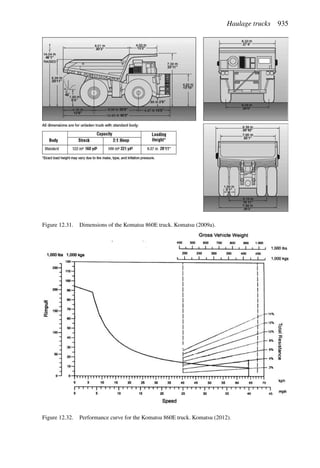
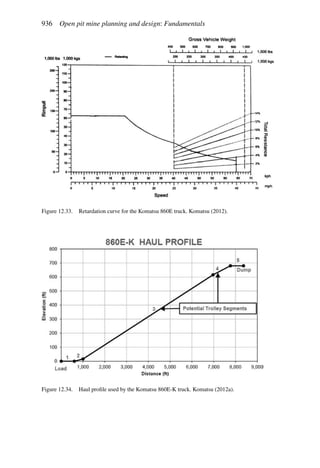
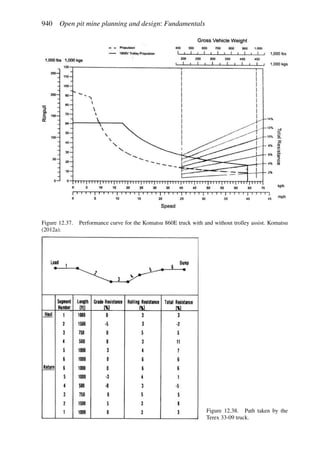
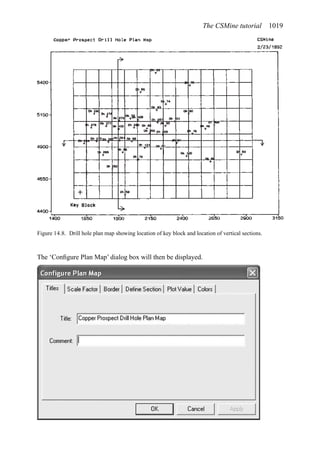
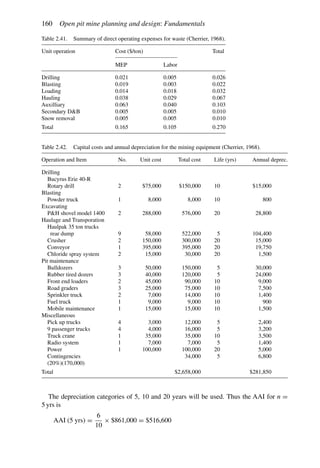
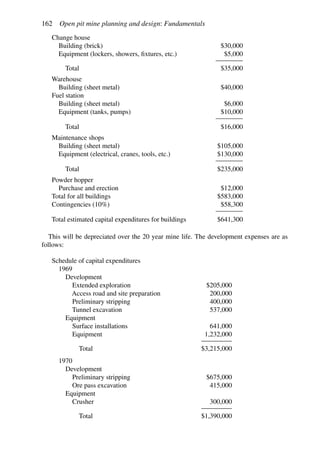
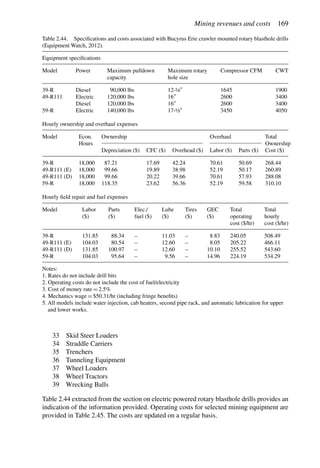
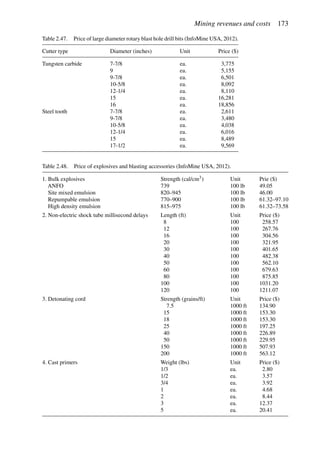
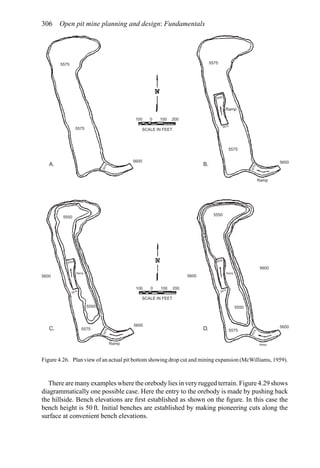
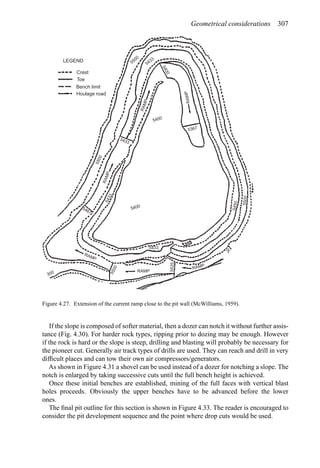
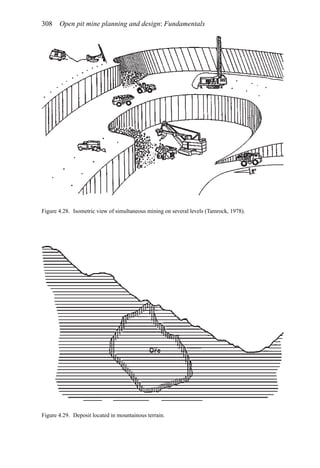
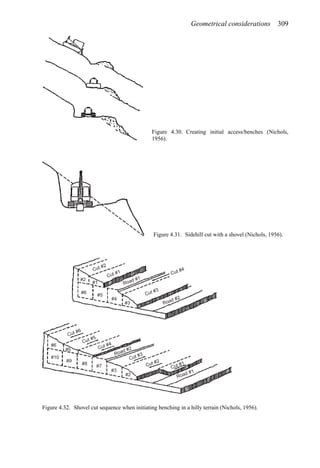
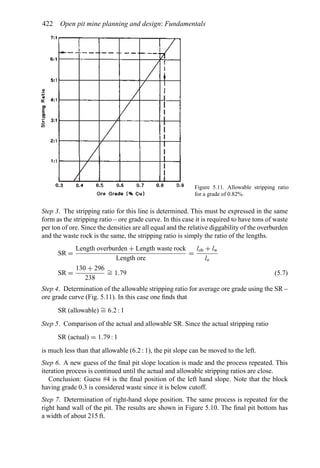
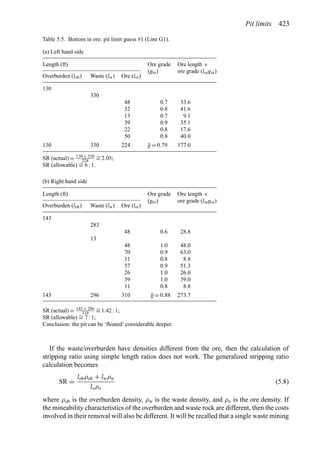
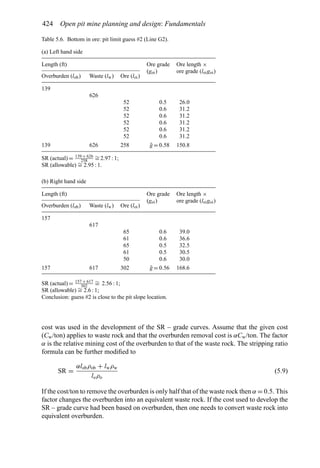
This document provides an overview of the fundamentals of open pit mine planning and design. It is the first volume of a multi-volume work on open pit mine planning and design by authors William Hustrulid, Mark Kuchta, and R. Martin. The document covers topics such as mine planning, estimating revenues and costs, orebody description methods, geometrical considerations, pit limits determination, production planning, and reporting of mineral resources and reserves.




































































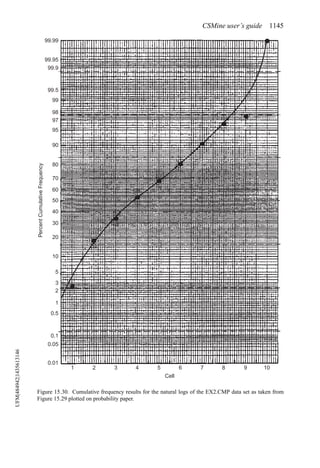
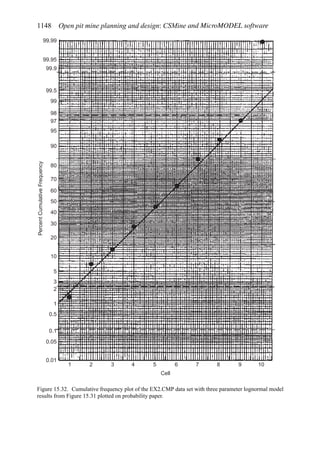
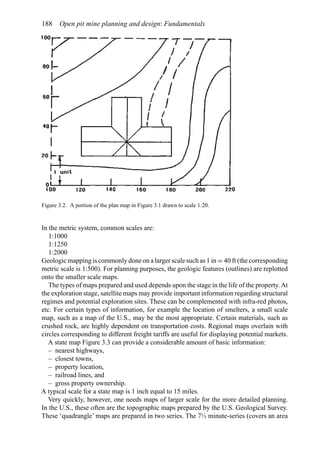
![50 Open pit mine planning and design: Fundamentals
where Am is the annual amount and [(1 + i)n
− 1]/i is the uniform series compound amount
factor.
The interest rate i which makes the future worths equal is called the rate of return (ROR)
on the investment.
In this case
$5(1 + i)10
= $1
(1 + i)10
− 1
i
Solving for i one finds that
i ∼
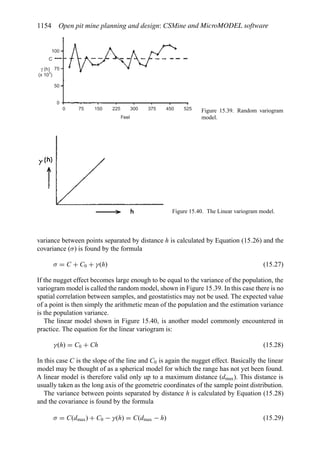
= 0.15
The rate of return is therefore 15%. One can similarly find the interest rate which makes
the net present value of the payments and the investment equal to zero at time t = 0.
NPV = −$5 + $1
(1.10)10
− 1
i(1 + i)10
= 0
i ∼
= 0.15
The answer is the same.
The process of bringing the future payments back to time zero is called ‘discounting’.
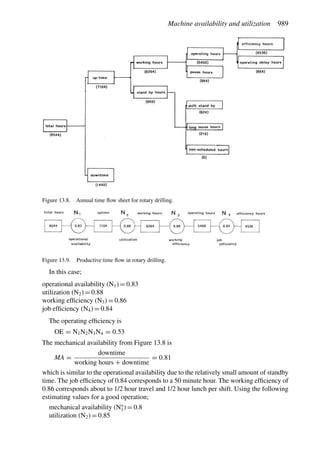
2.2.6 Cash flow (CF)
The term ‘cash flow’refers to the net inflow or outflow of money that occurs during a specific
time period. The representation using the word equation written vertically for an elementary
cash flow calculation is
Gross revenue
− Operating expense
= Gross profit (taxable income)
−Tax
= Net profit
− Capital costs
= Cash flow
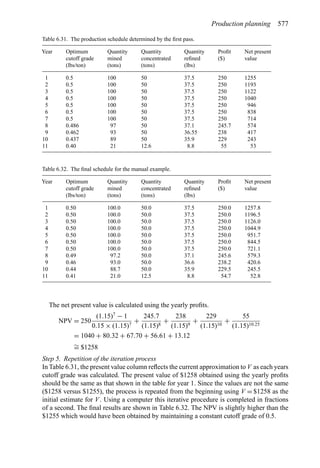
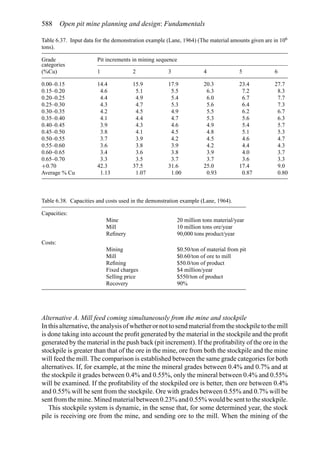
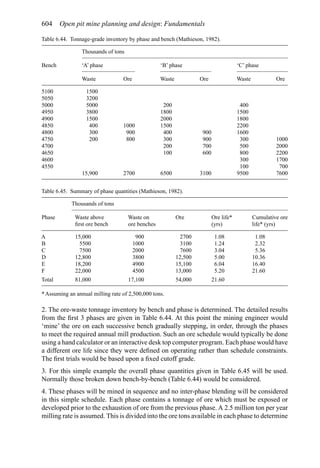
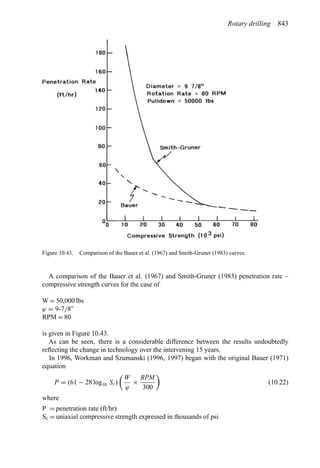
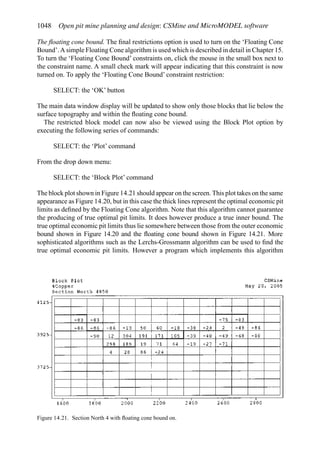
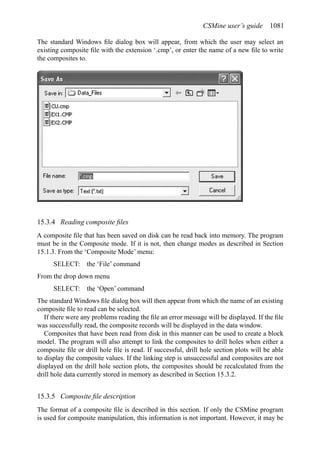
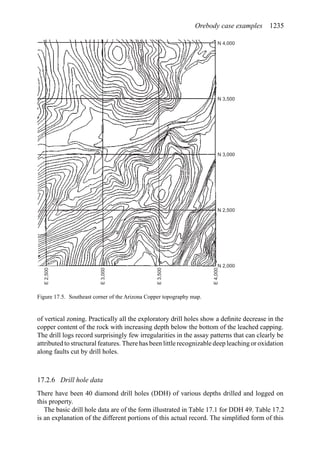
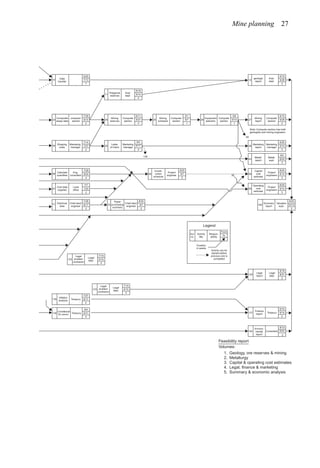
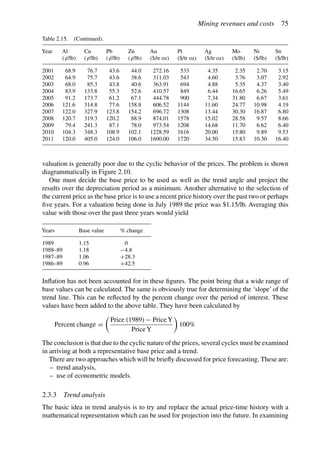
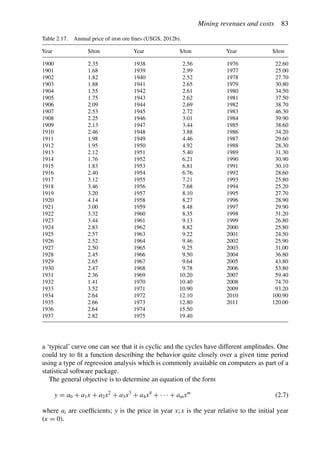
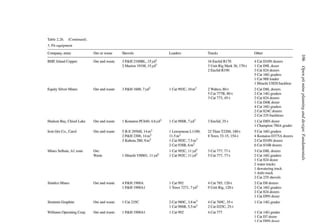
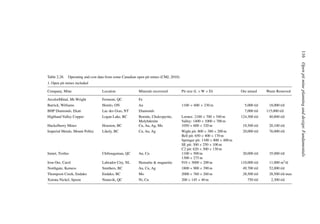
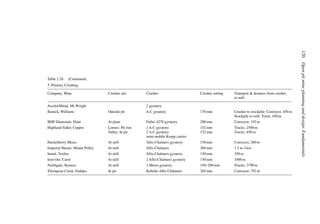
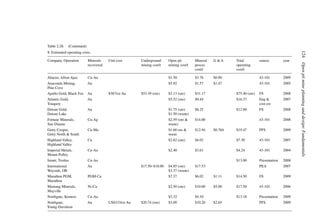
A simple example (after Stermole Stermole, 1987) is given in Table 2.1.
In this case there is a capital expense of $200 incurred at time t = 0 and another $100 at
the end of the first year. There are positive cash flows for years 2 through 6.
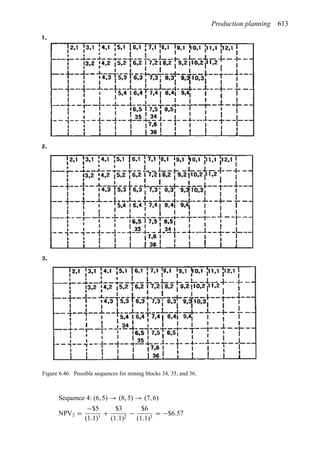
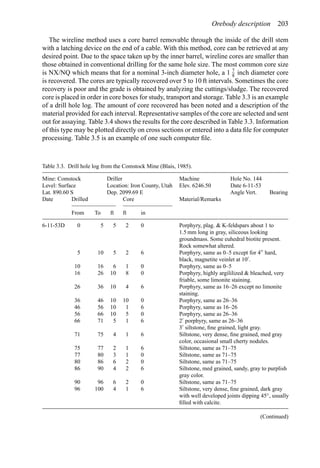
Table 2.1. Simple cash flow example (Stermole Stermole, 1987).
Year 0 1 2 3 4 5 6
Revenue 170 200 230 260 290
– Operating cost −40 −50 −60 −70 −80
– Capital costs −200 −100
– Tax costs −30 −40 −50 −60 −70
Project cash flow −200 −100 +100 +110 +120 +130 +140](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-71-320.jpg)




































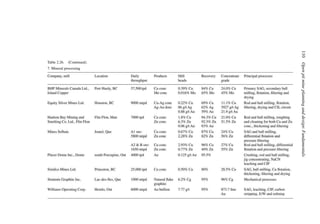







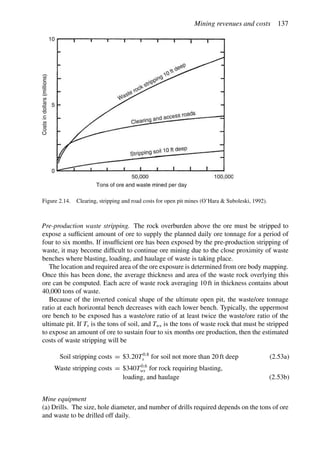




























































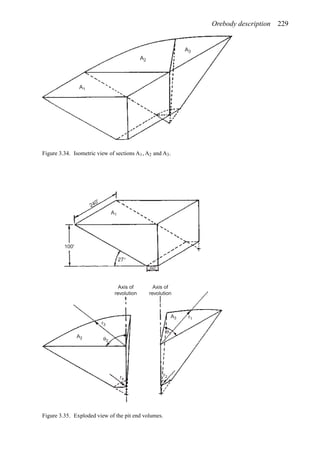

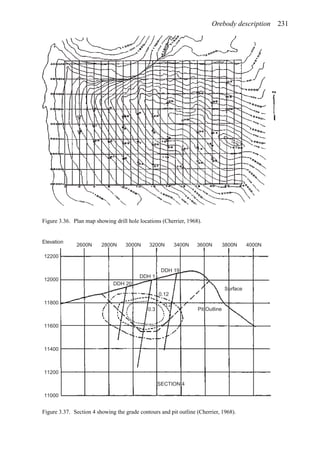
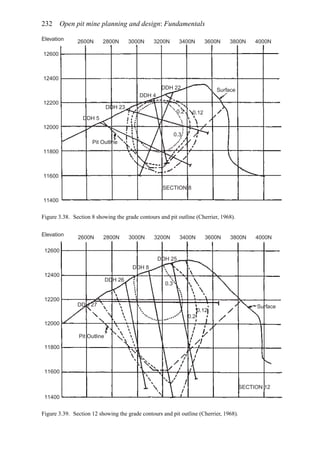
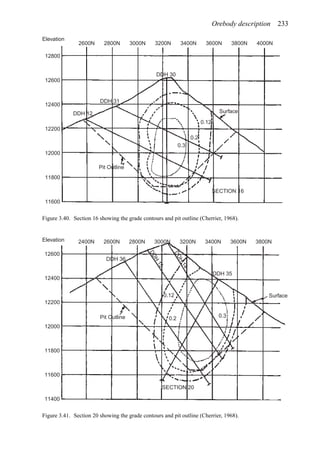











































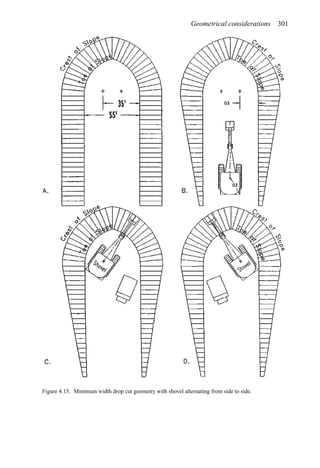


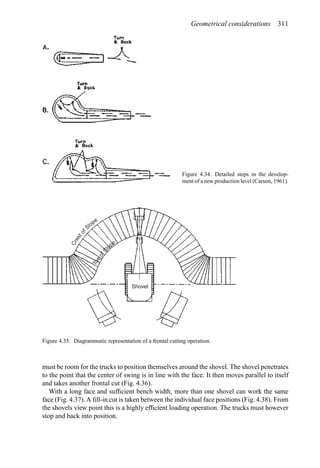
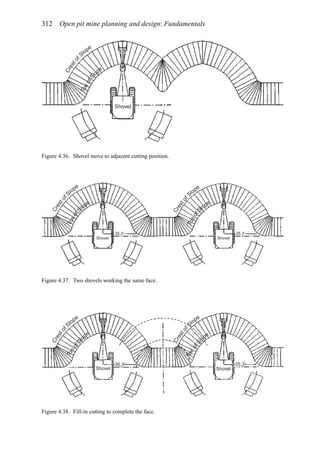
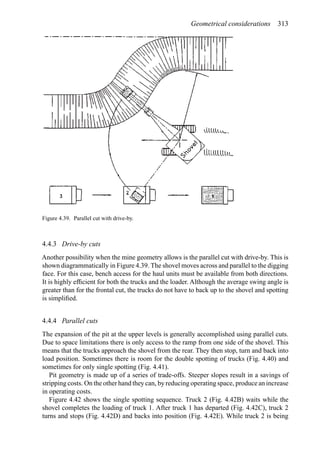
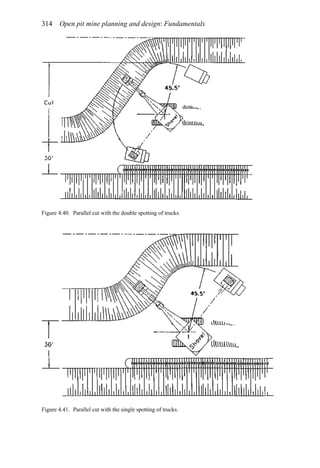
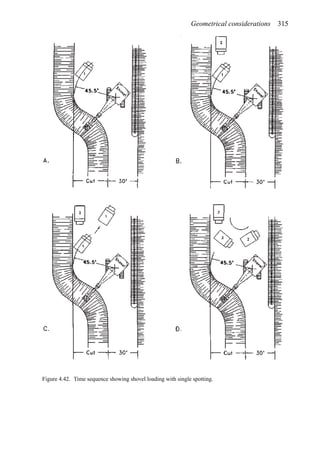

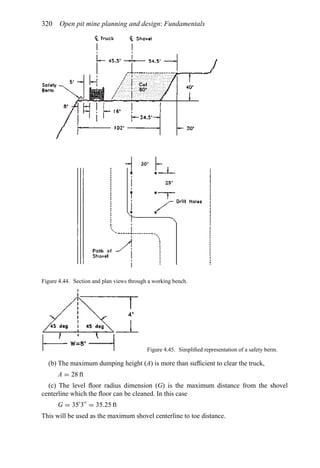




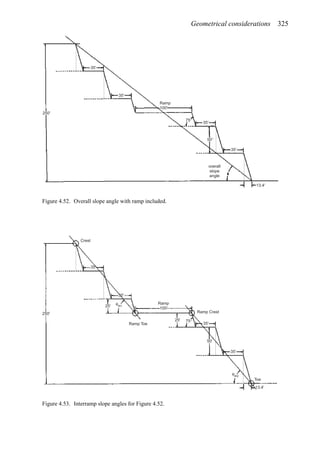
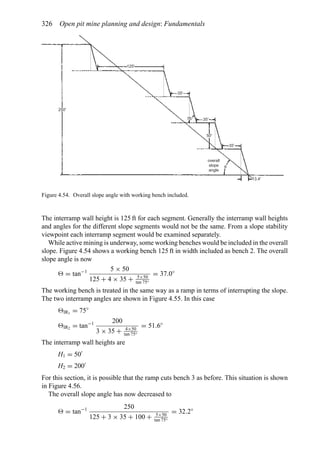

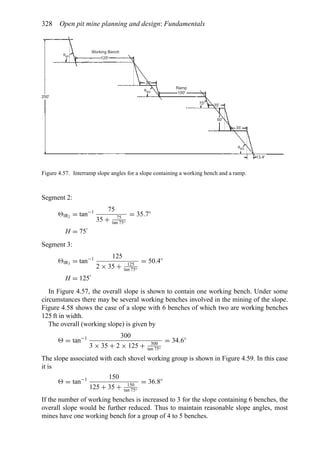














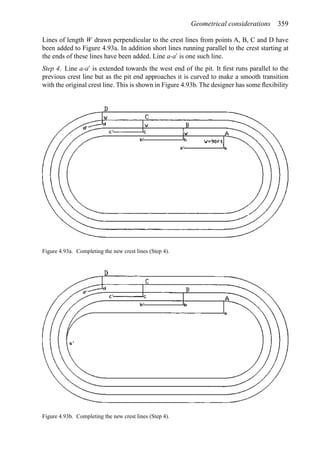
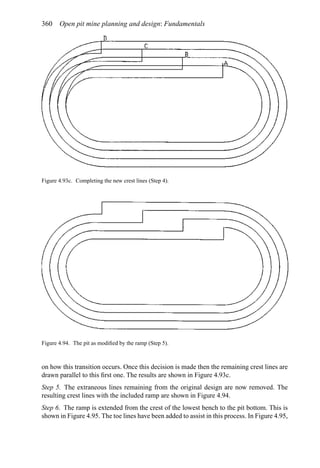

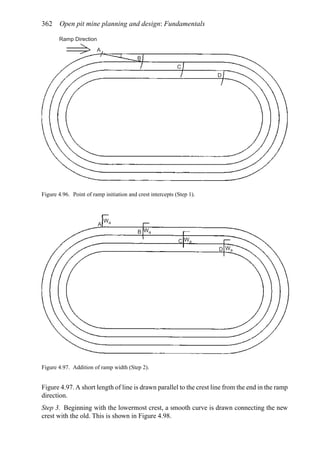
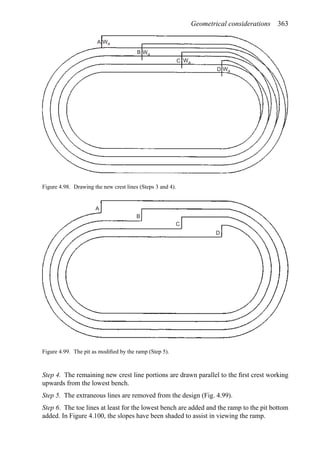


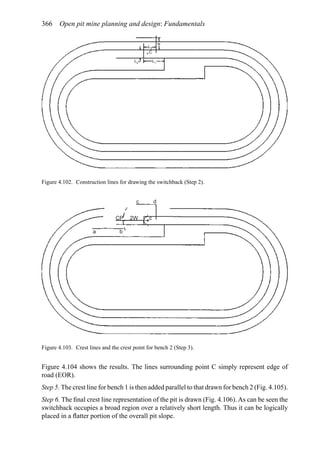

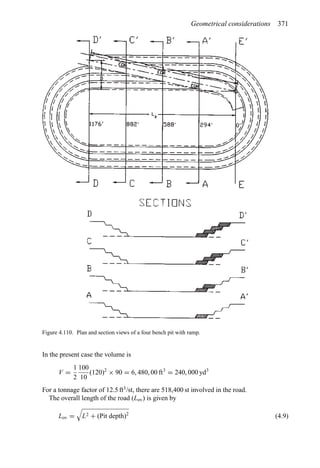








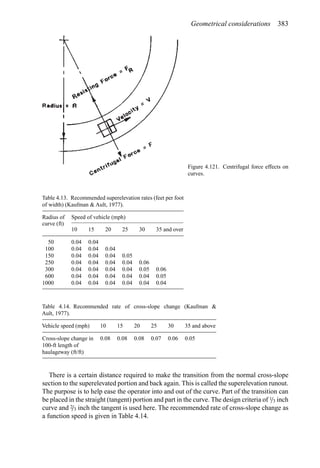
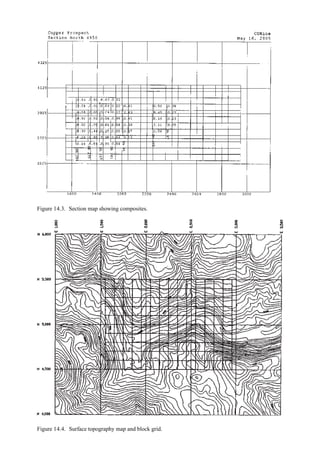
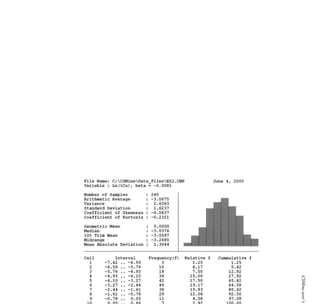
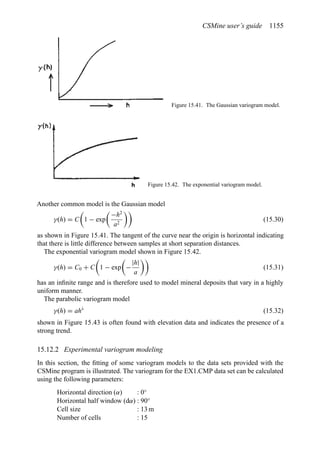
![384 Open pit mine planning and design: Fundamentals
To illustrate the use of this table, assume a vehicle is traveling at 35 mph on tangent with
normal cross slope 0.04 ft/ft to the right. It encounters a curve to the left necessitating a
superelevation rate of 0.06 ft/ft to the left. The total cross-slope change required is 0.10 ft/ft
(0.04 + 0.06). The table recommends a 0.05 ft/ft cross-slope change in 100 ft. Thus the
total runout length is computed as 200 ft [(0.10/0.05) × 100 = 200]. One-third of this length
should be placed in the curve and two-thirds on the tangent.
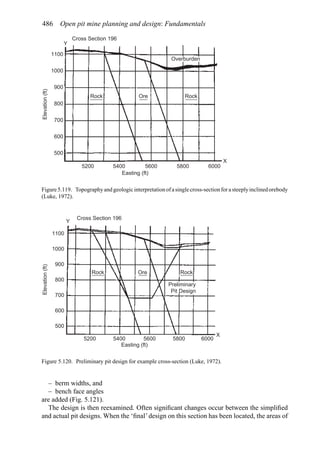
4.9.5 Conventional parallel berm design
U.S. federal law (MSHA, 1992) contains the following guidance regarding the need for
berms/guardrails in open pit mines (Section 57.9300):
(a) Berms or guardrails shall be provided and maintained on the banks of roadways where
a drop-off exists of sufficient grade or depth to cause a vehicle to overturn or endanger
persons in equipment.
(b) Berms or guardrails shall be at least mid-axle height of the largest self-propelled
mobile equipment which usually travels the roadway.
(c) Berms may have openings to the extent necessary for roadway drainage.
(d)Where elevated roadways are infrequently traveled and used only by service or mainte-
nance vehicles, berms or guardrails are not required (when certain very specific conditions
are met).
The principal purpose of these berms is to redirect the vehicle back onto the roadway and
away from the edge. Their effectiveness in this regard is controlled by berm face angle,
berm facing, the angle of incidence, and primarily by berm height. The stopping of runaway
vehicles is accomplished by median berms (Subsection 4.9.6) or special escapeways. One
negative effect of berms is the possibility of the vehicles overturning due to climbing the
sides.
There are two principal berm designs in common use today. The triangular or trapezoidal
shaped berm is generally formed from blasted materials. The sides stand at the angle of
repose of the material. The second type is the boulder-faced berm. Here, large boulders,
lined up along the haulage road, are backed with earthen material or blasted rock.
For the triangular berms, the design rule of thumb is that the height must be equal to or
greater than the static rolling radius (SRR) of the vehicle’s tire. For boulder-faced berms,
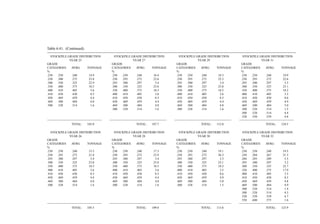
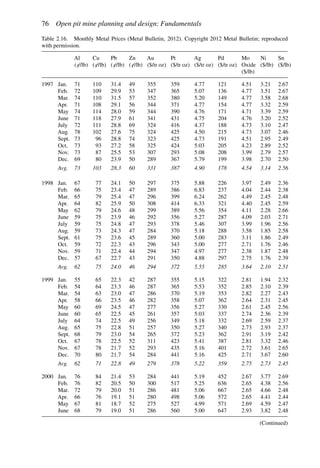
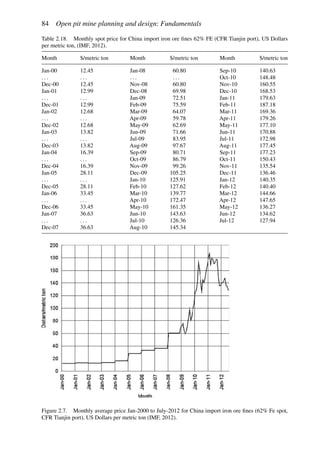
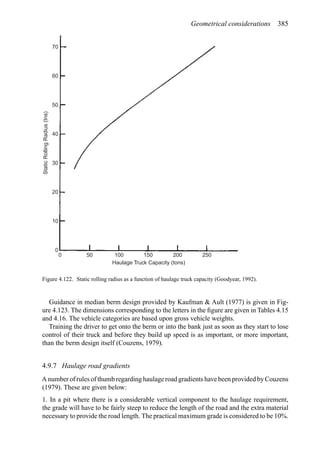
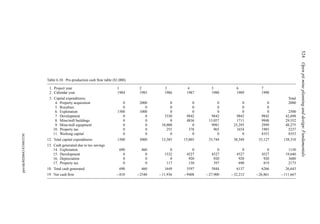
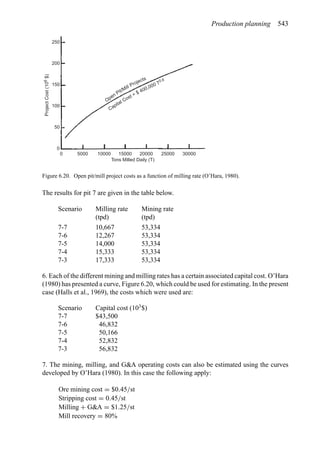
the height of the berm should be approximately equal to the tire height. Figure 4.122 shows
the relationship between the static rolling radius and haulage vehicle carrying capacity. Tire
height (TH) is about equal to:
TH = 1.05 × 2 × SRR (4.14)
4.9.6 Median berm design
Some means should be provided on haulroads to reduce truck speed or handle the truck that
loses its brakes. This is particularly true when long, downhill loaded hauls are involved.
Currently the most successful technique is through the use of median berms, also known
as ‘straddle berms’ or ‘whopper stoppers’ (Winkle, 1976a,b). These are constructed of sand
or some other fine grained material. The height of these berms is designed to impinge on
the under-carriage of the truck. Since the typical distance between the road surface to the
undercarriage is of the order of 2 to 3 ft for the range of available haulers, it is not necessary
to build a big barrier providing just another crash hazard.](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-405-320.jpg)




















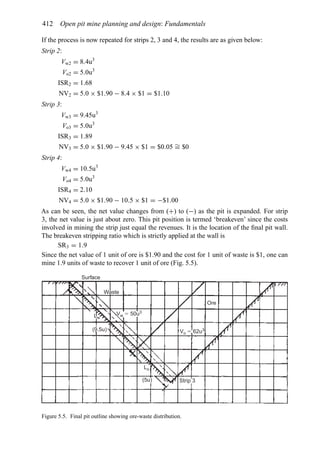









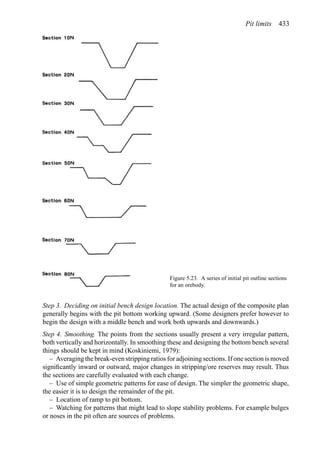






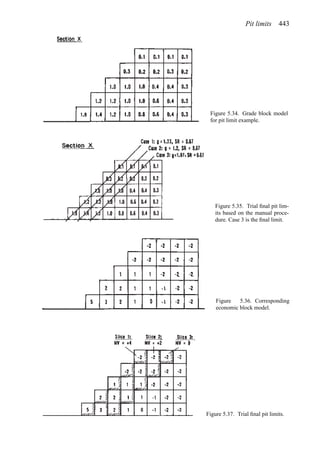










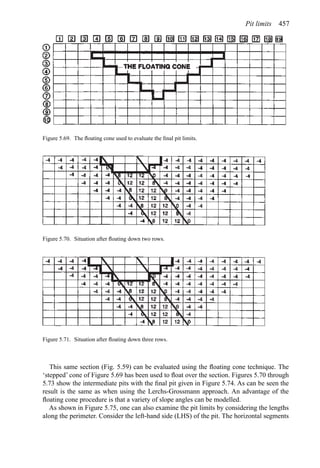


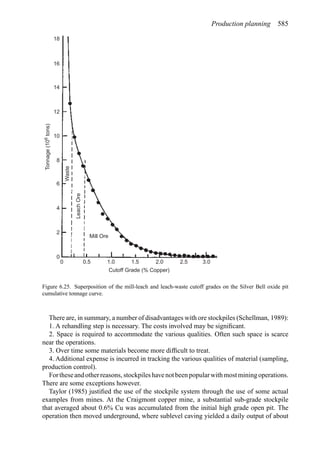
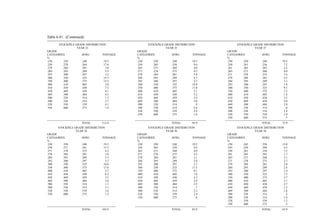
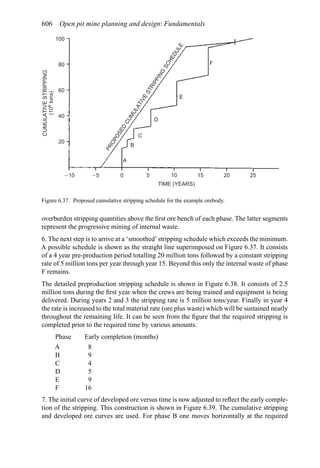
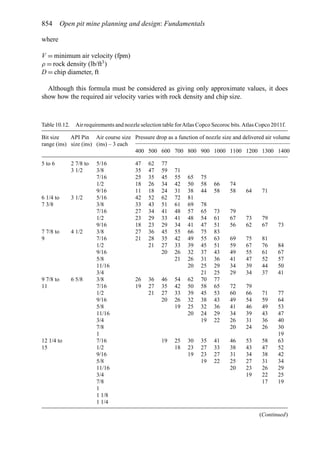
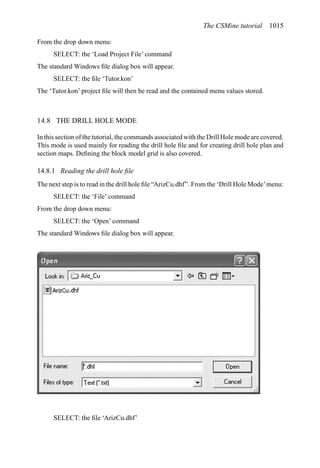
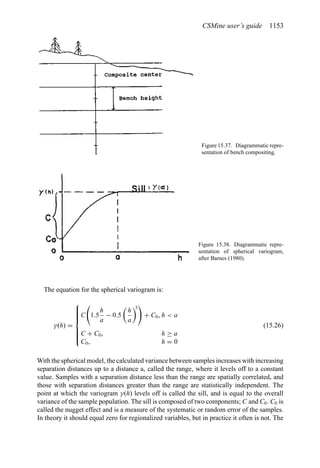
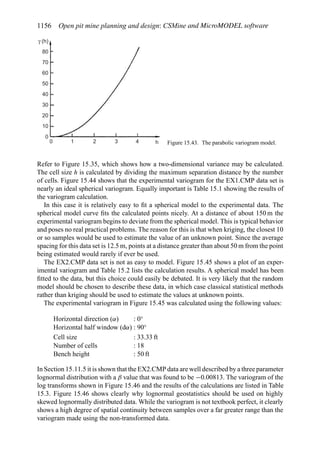
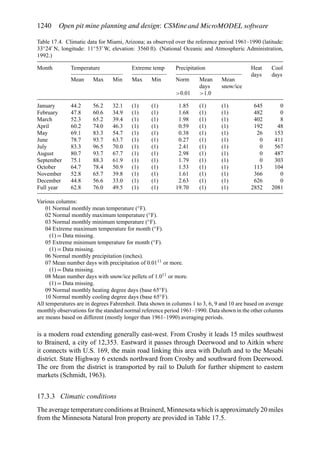
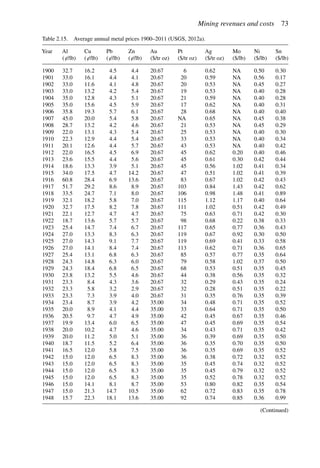
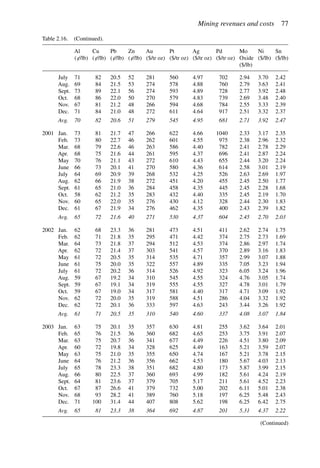
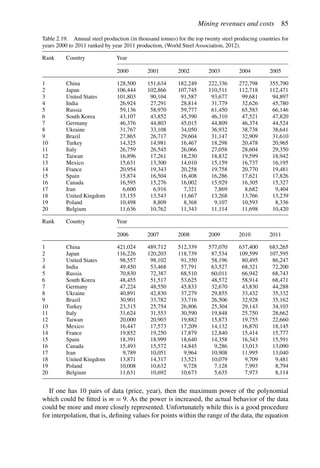
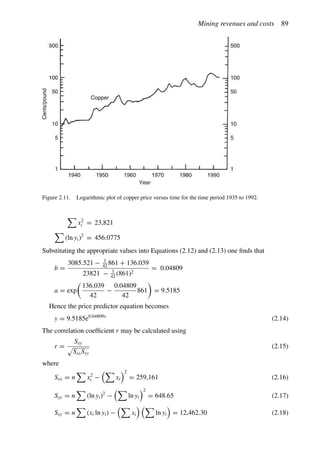
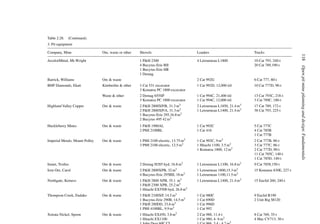
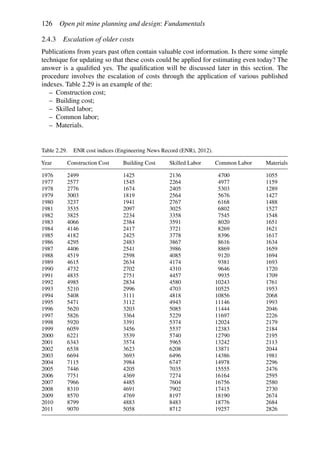
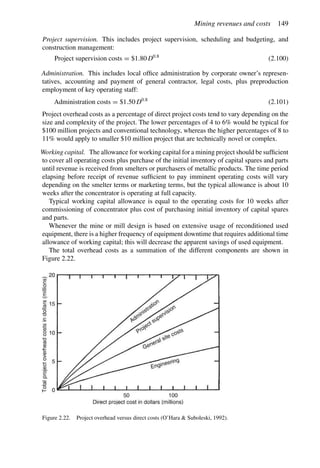
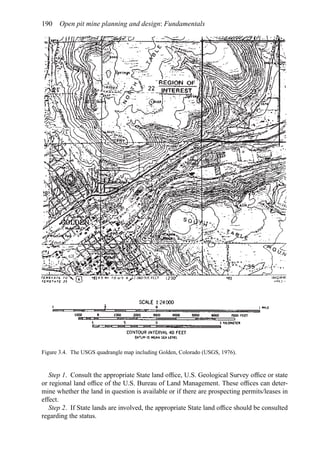
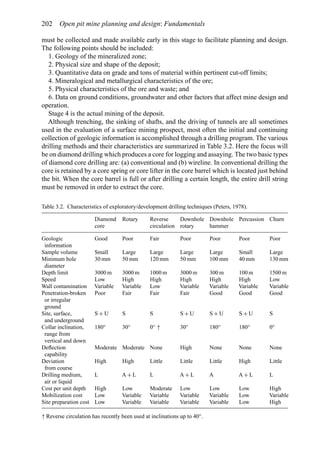
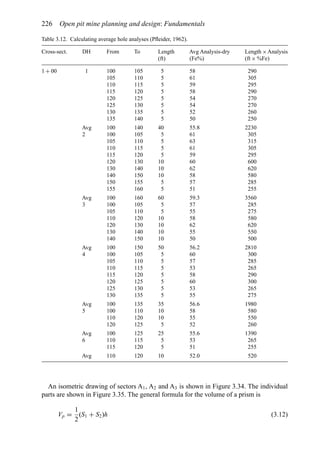
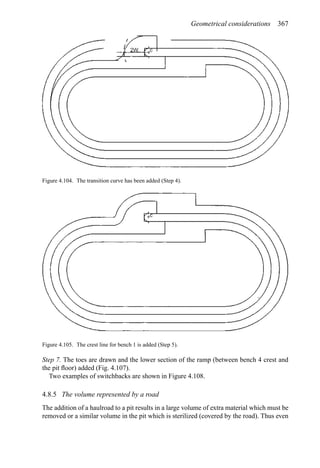
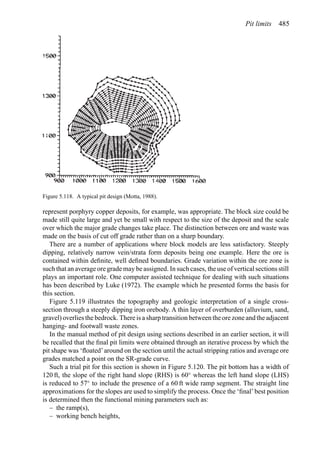
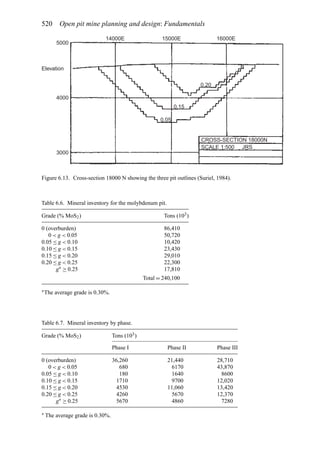
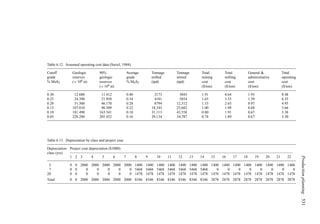
![Figure 5.79. Longitudinal section (Johnson Sharp, 1971).
Figure 5.80. Optimal longitudinal contour (Johnson Sharp,
1971).
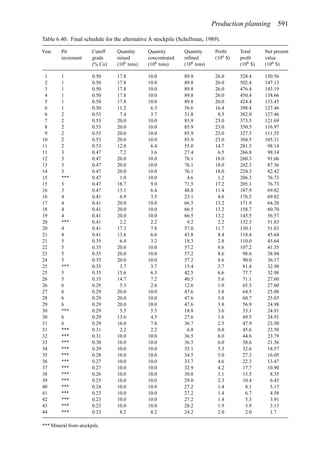
is found using a slightly modified version of the Lerchs-Grossmann 2-D algorithm. The
net values for each of the four pits on this section are then determined. As can be seen
these are:
Level 1: S11 = 2
Level 2: S12 = −3
Level 3: S13 = 1
Level 4: S14 = −7
To combine all of the transverse (ik) sections, a longitudinal section will now be taken. In
viewing Figure 5.78, it is seen that the deepest mining on section 1 ( j = 1) occurs at column
i = 4. A column [i = 4, j = 1 (section 1)] of blocks will now be formed representing the net
value of the cross-section as mined down to the various levels.
The net value for the material contained within the pit is found by summing the block
values along the final contour. Here it becomes
Pit value = 2 + 0 + 5 + 0 − 1 = 6
Now that the bottom levels for each of the transverse sections have been determined, one
goes back to these sections and selects the appropriate one. These are summarized in
Figure 5.81.
The data and solution for a somewhat more complicated problem are given in Figures
5.82 and 5.83, respectively. The block height to length ratio along the longitudinal section
(the axis of mineralization) is 1 to 2 while for the cross-sections the block height and length
are equal (1 to 1). Hence to maintain a maximum pit slope of 45 degrees, the pit slope can
change by two blocks per section along the length but by only block per column across the
width.
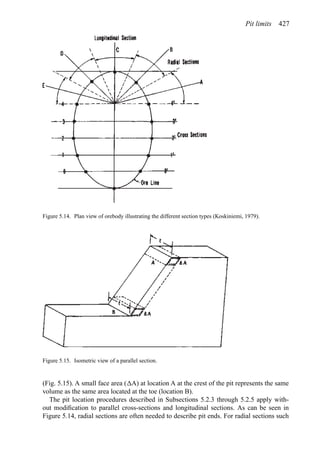
Pit limits 461](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-482-320.jpg)











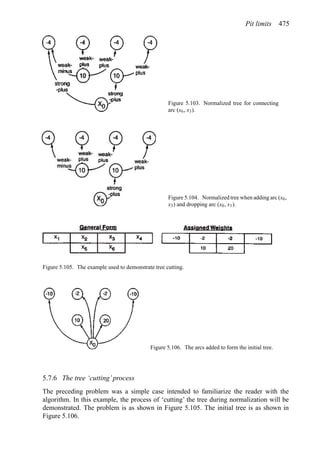




















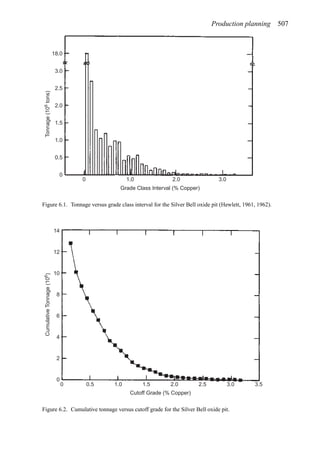
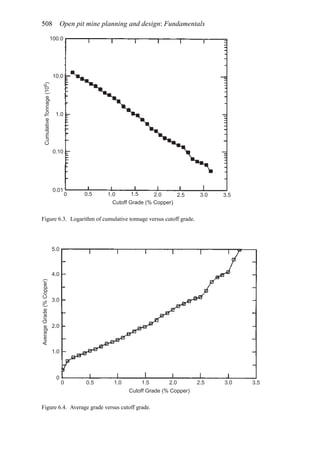

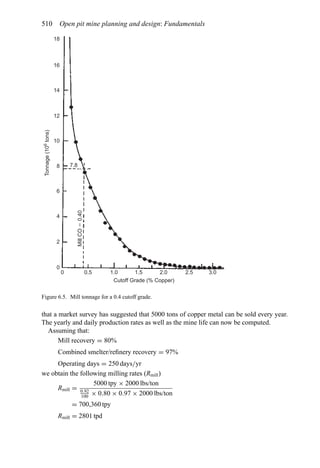
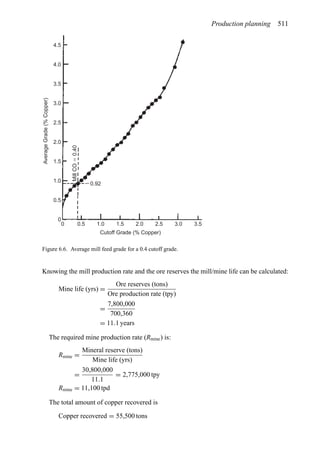

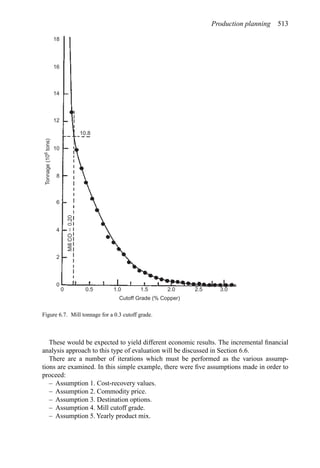
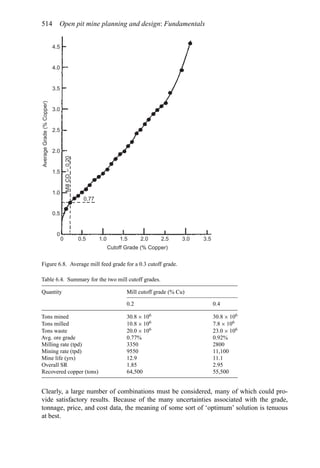



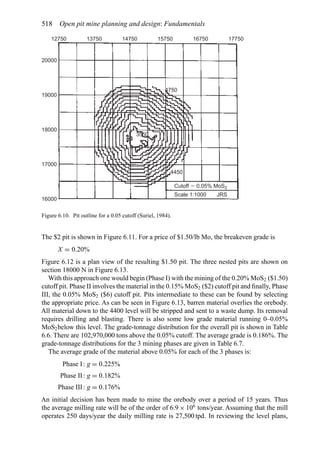
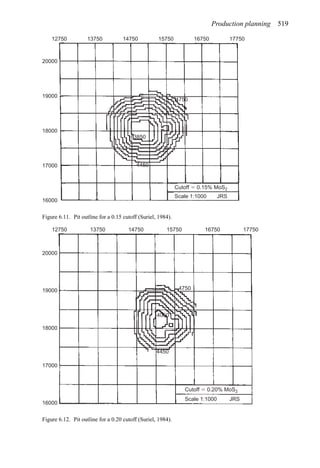









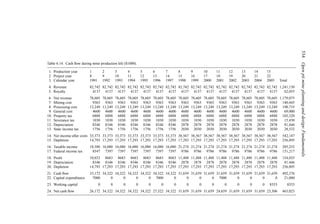






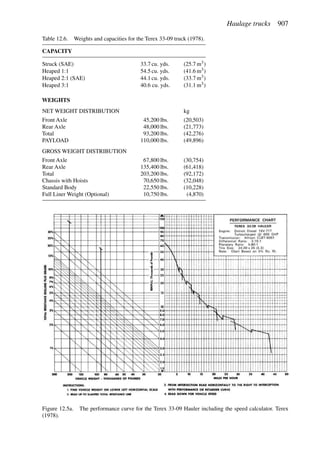
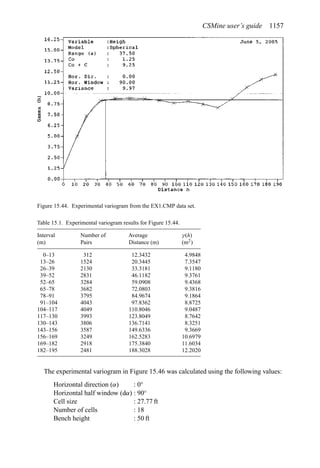
![Production planning 541
Solving for the cutoff grade one finds that
Grade (%) =
[Mining ($/st) + Milling ($/st) + GA ($/st)]104
[Price ($/lb) − SRS ($/lb)]2000 × Recovery (%)
(6.6)
If the expected price is used then the maximum (ultimate) pit will result.
2. The grades and tonnage in the pit are determined. This becomes the reserve of material
to be mined.
Assume the following values:
Mining cost = $0.45/st
Milling + GA = $1.25/st
Price = $0.40/lb
SRS = $0.059/lb
Recovery = 80%
(Note that for simplicity the GA has been applied only to the mill (i.e. the ore).)
Then the mining cutoff grade becomes
Grade (%) = 0.31%
One would generate a pit with this as the cutoff.
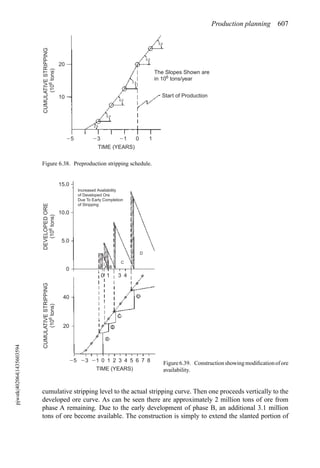
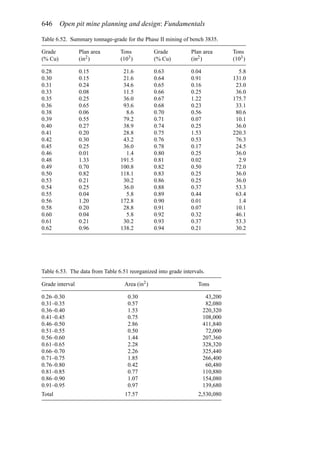
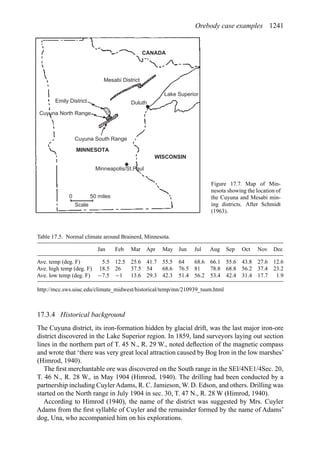
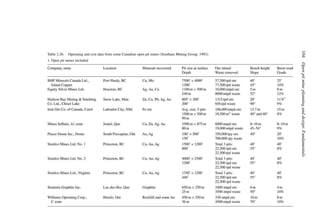
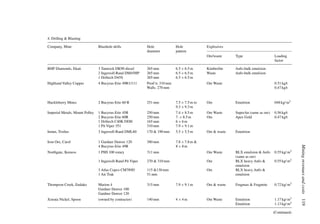
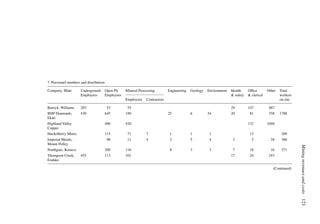
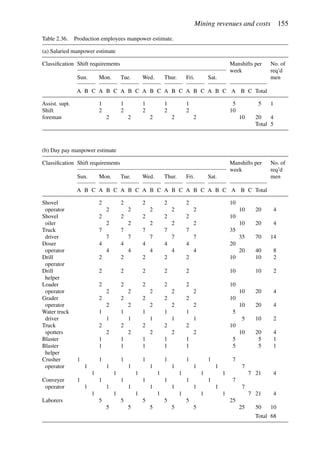
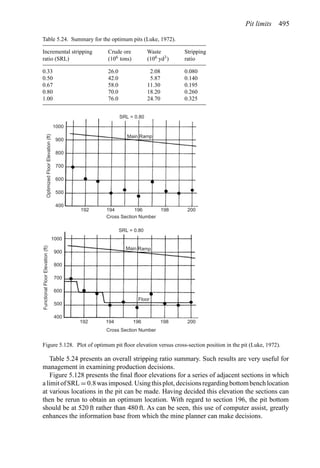
Table 6.16 shows that for a pit based upon a 0.3% Cu pit limit cutoff, the tonnage would
be 1,410,000,000. The average grade would be 0.31% Cu (all material). If the mill cutoff
grade were 0% then the entire amount would be sent to the mill. If only those blocks having
a grade of +0.3% were sent to the mill, then the mill tonnage would be 390,000,000 having
an average grade of 0.73% Cu. This would be the largest pit.
3. One could consider smaller pits as well since the biggest pit would not necessarily lead
to the desired financial result. This result could be measured in NPV, total profit, return
on investment, etc. Other pits can be generated corresponding to different pit limit cutoff
grades. As can be seen from Equation (6.6), this is a simple matter of just changing the
price. For a lower price, the cutoff grade must go up. In Table 6.16 the following results
were obtained.
Pit limit Total tons Avg. grade
cutoff grade in pit (% Cu)
(% Cu) (× 106
st)
0.3 1410 0.31
0.4 1206 0.33
0.5 875 0.36
0.6 650 0.38
0.7 400 0.40
For each of these ultimate pits all the material would be mined. One must decide whether it
should go to the dump or to the mill.
4. Each of the potential pits is examined with respect to mill and dump material. Consider
the pit developed assuming a final pit cutoff grade of 0.7%. The mill cutoff could be set at](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-562-320.jpg)



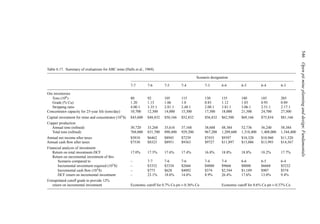
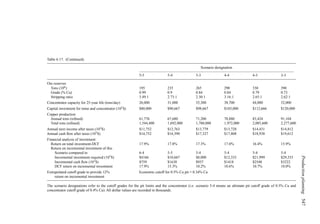




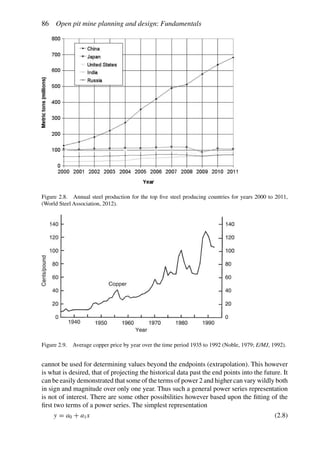
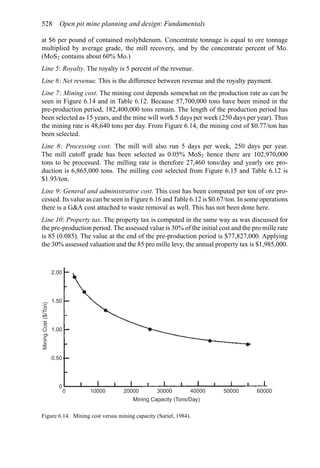
![552 Open pit mine planning and design: Fundamentals
There are a great number of possible mine, concentrator and refinery operating combi-
nations. Which is the optimum? In this section the basic equations will be developed in
addition to demonstrating the process. However, prior to beginning the theoretical treat-
ment, it is considered useful to briefly consider just one of these operating combinations.
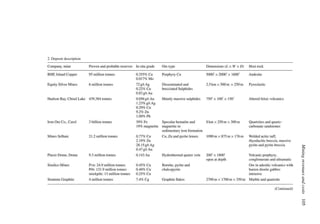
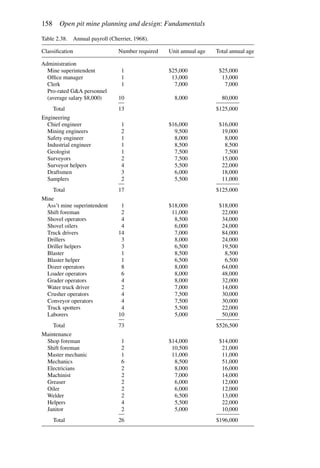
The total amount of material to be mined Qm is 1000 tons. If the mine is operated at capacity
(100 tons/year) then the pit would be mined out over a time period of 10 years. Assuming
that the grades (Table 6.19) are equally distributed throughout the pit and a concentrator
cutoff grade of 0.50 lbs/ton is used, then 50 tons of material having an average grade of
0.75 lbs/ton would be sent to the concentrator every year. The other 50 tons would be sent
to the waste dump. Since the concentrator capacity C is 50 tons/year, this is an accept-
able situation. The concentrator product becomes the refinery feed. In this case it would
be 37.5 lbs/year (0.75 lbs/ton × 50 tons/year). Since the refinery can handle 40 lbs/year, it
would be operating at below its rated capacity R. This combination of mining rate and cutoff
grade would yield a yearly profit Py of
Py = (25 − 5)37.5 − 2 × 50 − 1 × 100 − 300 = $250
These profits would continue for 10 years and hence the total profit would be $2500. The
NPV assuming an interest rate of 15% would be
NPV =
250[(1.15)10
− 1]
0.15(1.15)10
= $1, 254.69
The first question to be asked is whether some other combination of mine production rate
and concentrator cutoff grade would yield a better profit from this deposit? The larger
question is whether the various plant capacities (with their associated costs) are optimum?
The procedure described in this section is a way of determining the combination yielding the
maximum profit for a given set of operating constraints. The constraints may then be changed
(mine, concentrator and refining capacities, for example) and the profit corresponding to
this new combination determined as well as how the various capacities should be utilized
over the life of the pit.
6.7.5 Cutoff grade for maximum profit
Step 1. Determination of the economic cutoff grade – one operation constraining the total
capacity
As indicated, the basic profit expression (6.10) is
P = (s − r)Qr − cQc − mQm − f T
Calculate cutoff grade assuming that the mining rate is the governing constraint. If the
mining capacity M is the applicable constraint, then the time needed to mine material Qm is
Tm =
Qm
M
(6.11)
Equation (6.10) becomes
P = (s − r)Qr − cQc −
m +
f
M
Qm (6.12)
Tofindthegradewhichmaximizestheprofitunderthisconstraintonefirsttakesthederivative
of (6.12) with respect to g.
dP
dg
= (s − r)
dQr
dg
− c
dQc
dg
−
m +
f
M
dQm
dg
(6.13)](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-573-320.jpg)




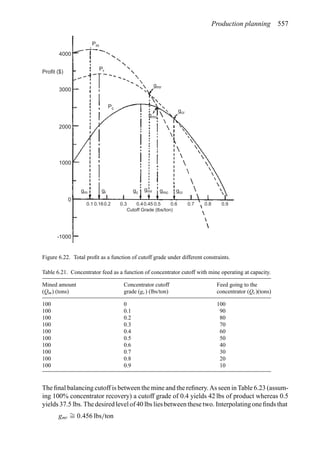










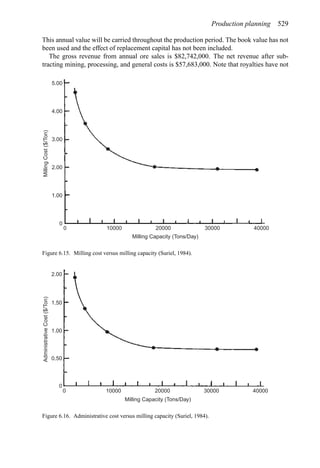
![568 Open pit mine planning and design: Fundamentals
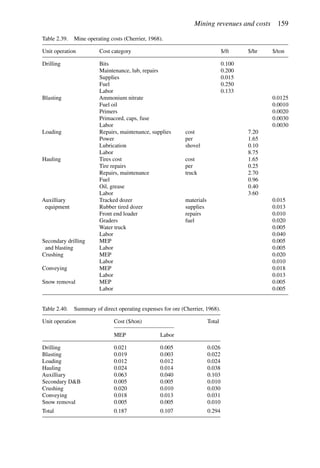
Thus the concentrating capacity is violated. The result is that the concentrator is the
bottleneck.
In the further calculations
Qm = 83.3
Qc = 50
Qr = 35
The profit from time period T is expressed as
P = (s − r)Qr − cQc − mQm − f T
For T = 1 year one finds that
P = (25 − 5) × 35 − 2 × 50 − 1 × 83.3 − 300 × 1 = $216.7
Since the total amount of material to be mined from the pit is Q = 1000 units, the number
n of years required is
n =
1000
83.3
= 12 years
The present value V corresponding to 12 equally spaced payments of P = $216.7 using an
interest rate of 15 percent is
V =
216.7[1.1512
− 1]
0.15(1.15)12
= $1174.6
This value of V becomes the second approximation of V (the first was V = 0) for use in the
formulas to calculate gc and gr.
gc =
c + f +dV
C
y(s − r)
=
2 + 300+0.15×1174.6
50
25 − 5
= 0.576
gr =
c
s − r − f +dV
R
y
=
2
20 − 300+0.15×1174.6
40
= 0.247
The new six choices become
gm = 0.10
gc = 0.576
gr = 0.247
gmc = 0.50
grc = 0.60
gmr = 0.456
Applying the rules to select the overall pair optimum yields
Gmc = 0.50
Grc = 0.576
Gmr = 0.247](https://image.slidesharecdn.com/open-pit-mine-planning-and-design-hustrulid-william-a-230817104213-4a3a90e5/85/Open-pit-mining-pdf-589-320.jpg)