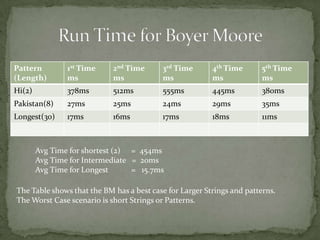
The document discusses two string matching algorithms: Knuth-Morris-Pratt (KMP) and Boyer-Moore (BM). KMP runs in linear time but checks every character, while BM can be sub-linear as it does not need to check every character. The document provides pseudocode examples and comparisons of the running times of KMP and BM on different length patterns, finding that BM performs best on longer patterns while KMP has better performance on shorter patterns. Both algorithms have widespread applications in areas like web search engines, spam filters, and natural language processing.

1. BCS-4
Exact String Matching
COMSATS Institute Of Information Technology, wah

2.  Ehtisham Arshad (FA11-BsCS-059)
 Hissam Yousaf (Sp12-BsCS-036)

3. Exact String Matching Algorithms
 Knuth Morris And Pratt – KMP
 Boyer Moore - BM

4. The goal of any string-searching algorithm is to
determine whether or not a match of a particular
string exists within another (typically much longer)
string.
Many such algorithms exist, with varying efficiencies.
• Knuth Morris And Pratt - KMP
• Boyer Moore - BM

5.  Introduction
The algorithm was conceived in 1974 by Donald
Knuth and Vaughan Pratt, and independently by James H.
Morris. The three published it jointly in 1977
 KMP, linear time algorithm for the string matching
problem, every character is checked.

6.  Introduction
Developed in 1977, the BM string search algorithm is a
particularly efficient algorithm.
 This algorithm’s execution time can be sub-linear, as not
every character of the string to be searched needs to be
checked.

8.  Left to Right Check
Scans the string from left to right to match a particular
given pattern
 If a match is found at the first index, the next index is
checked otherwise the pointer moves to right of the
string
 Character Skip using KMP table
Partial_lenght – 1 (for Initial Match)
Partial_lenght – index value = SKIP

9.  Step 1:compare p[1] with S[1]
S a b c a b a a b c a b a c
p
a b a a
 Step 2: compare p[2] with S[2]
a b c a b a a b c a b a c
a b a a

10.  Step 3: compare p[3] with S[3]
S
a b c a b a a b c a b a c
P
a b a a
Mismatch occurs here..
Since mismatch is detected, shift ‘p’ one position to the left and
perform steps analogous to those from step 1 to step 3.

11.  Final Step:
S
P
a b c a b a ab c a b a c
ab aa
Finally, a match would be found after shifting ‘p’ three times to the right
side.

13.  Bad Character Rule
Occurs when rightmost character of the pattern
doesn’t match with the given string’s index.
 Good Suffix Rule
If a number of characters match with the given string
then the good suffix shift occurs.

14.  Step 1: Try to match first m characters
Pattern: STING
String: A STRING SEARCHING EXAMPLE
CONSISTING OF TEXT
This fails. Slide pattern right to look for other matches.
Since R isn’t in the pattern, slide down next to R.

15.  Step 2:
Pattern : STING
String : A STRING SEARCHING EXAMPLE
CONSISTING OF TEXT
Fails again.
Rightmost character S is in pattern precisely once, so slide
until two S's line up.
String : A STRING SEARCHING EXAMPLE
CONSISTING OF TEXT
No C in pattern. Slide past it.

16.  Final Step:
Pattern : STING
String : A STRING SEARCHING EXAMPLE
CONSISTING OF TEXT
Match found..

17. Pattern
(Length)
1st Time
(ms)
2nd Time
(ms)
3rd Time
(ms)
4th Time
(ms)
5th Time
(ms)
Hi(2)
8ms
9ms
6ms
10ms
9ms
Pakistan(8)
20ms
19ms
22ms
20ms
21ms
Longest(30)
38ms
46ms
39ms
37ms
43ms
Avg Time for shortest (2) = 8.4ms
Avg Time for Intermediate = 20.4ms
Avg Time for Longest
= 40.6ms
The Table shows that the KMP has a best case for Short Strings and patterns.
The Worst Case scenario are Larger Strings or Patterns.

18. Pattern
(Length)
1st Time
ms
2nd Time
ms
3rd Time
ms
4th Time
ms
5th Time
ms
Hi(2)
378ms
512ms
555ms
445ms
380ms
Pakistan(8)
27ms
25ms
24ms
29ms
35ms
Longest(30)
17ms
16ms
17ms
18ms
11ms
Avg Time for shortest (2) = 454ms
Avg Time for Intermediate = 20ms
Avg Time for Longest
= 15.7ms
The Table shows that the BM has a best case for Larger Strings and patterns.
The Worst Case scenario is short Strings or Patterns.

19. Processing time (ms)
 On average, for sufficiently large alphabets (8 characters) BoyerMoore has fast running time and sub-linear number of character
comparisons.
 On average, and in worst cases Boyer-Moore is faster than “BoyerMoore-like” algorithms.

20.  The running time of Knuth-Morris-Pratt algorithm is
proportional to the time needed to read the characters
in text and pattern. In other words, the worst-case
running time of the algorithm is O(m + n) and it
requires O(m) extra space.

21. • Boyer requires a preprocessing time of O(m+∂)
• The running time of BM algorithm is O(mn)
• The Boyer Moore Algorithm performs best for
O(n/m)
•
• Worst Case of BM is 3n.

22. KMP and Boyer Moore finds its applications in many
core Digital Systems and processes e.g.
 Digital libraries
 Screen scrapers
 Word processors
 Web search engines
 Spam filters
 Natural language processing

23. Thank you