KMP pattern searching allows efficient searching of a pattern within text by taking advantage of prefix matches. It works by pre-processing the pattern to construct a prefix table indicating the length of matching prefix for all prefixes of the pattern. During searching, when a mismatch occurs, it uses the prefix table to "skip" already compared prefix matches, avoiding repeating comparisons and allowing it to run in linear time O(n+m).

1. KMP Pattern Search
QUICK OVERVIEW
Created by,
Arjun SK
arjunsk.com

2. What is Patter Searching ?
o Suppose you are reading a text document.
o You want to search for a word.
o You click CTRL + F and search for that word.
o The word processor scans the document and shows the position of
occurrence.
What exactly happens is that, word i.e. pattern is searched inside the
text document.

3. Implementation

4. Naïve Approach
The naïve approach is to check whether the pattern matches the string
at every possible position in the string.
P = Pattern (word) of length m
T = Text (document) of length n
Naive string matching algorithm
takes time O((n-m+1)m)

5. Basic Idea of KMP
a b c d a b c a a a b c b a b
a b c d a b c d
Text
Pattern
Text
Pattern
We can find the next position for comparison, by looking at the pattern.
a b c d a b c a a a b c b a b
a b c d a b c d

6. KMP (Knuth-Morris-Prattern String Matching Algorithm)
Why KMP?
Best known for linear time for exact pattern matching.
How is it implemented?
o We find patterns within the search pattern.
o When a pattern comparison partially fails, we can skip to next
occurrence of prefix pattern.
o In this way, we can skip trivial comparisons.

7. Pre-processing
Let’s say we’re matching the pattern “abababca” against the text
“bacbababaabcbab”.
Here’s our prefix match table : i.e. prefix-table[i]
index 0 1 2 3 4 5 6 7
char a b a b a b c a
value 0 0 1 2 3 4 0 1
Matching prefix i.e. a
Matching prefix i.e. ab
Matching prefix i.e. aba
Matching prefix i.e. abab
No matching prefix

8. Pre-processing - cont.
• partial_match_length = length of the matched pattern in a step.
• prefix-table = pre-processed prefix table
• If prefix-table[ partial_match_length ] > 1
we may skip ahead
partial_match_length - prefix-table[ partial_match_length – 1 ] characters.
// Used to skip, already compared prefix match in the pattern.

9. Searching
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
This is a partial match length of 1
The value at prefix-table[partial_match_length - 1] (or prefix-table[0]) is 0.
so we don’t get to skip ahead any.

10. b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern

11. b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
In naïve approach we shift right and compare again:
Step 2
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
Step 1
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern

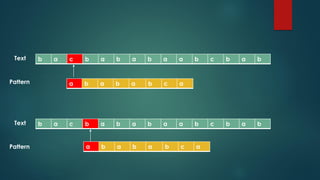
12. But in KMP approach, we can directly skip Step 1
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
X X
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
This is a partial match length of 5
The value at prefix-table[partial_match_length - 1] (or prefix-table[4]) is 3.
That means we get to skip ahead
partial_match_length – prefix-table[partial_match_length - 1] (or 5 - table[4] = 5 - 3 = 2) characters:
We skip comparing “b”. The next comparison starts at next “ab” i.e. the prefix match.

13. In KMP we can directly skip comparing “ab”
This is a partial match length of 3
The value at prefix-table[partial_match_length - 1] (or prefix-table[2]) is 1.
That means we get to skip ahead
partial_match_length – prefix-table[partial_match_length - 1] (or 3 - table[2] = 3 - 1 = 2) characters:
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern
b a c b a b a b a a b c b a b
a b a b a b c a
Text
Pattern X X
We skip comparing “b”. The next comparison starts at next “a” i.e. the prefix match.

14. Complexity
 O(m) - It is to compute the prefix function values.
 O(n) - It is to compare the pattern to the text.
 Total of O(n + m) run time.