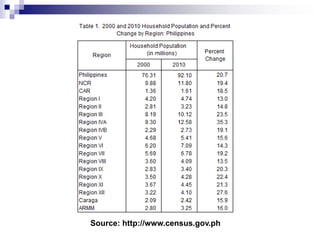
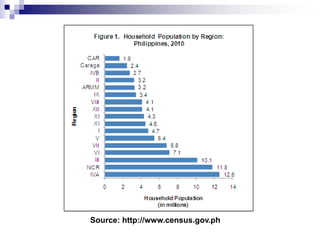
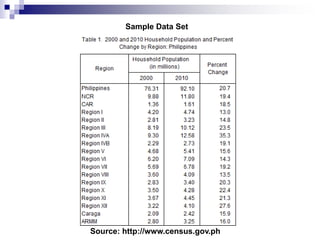
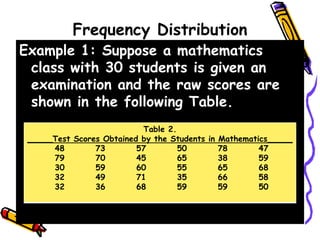
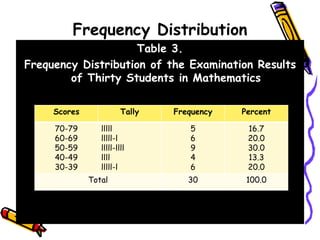
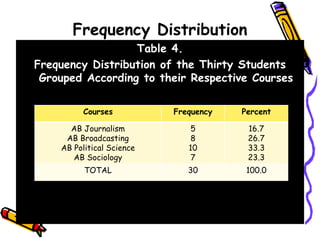
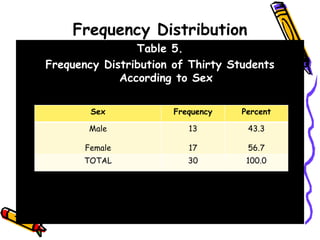
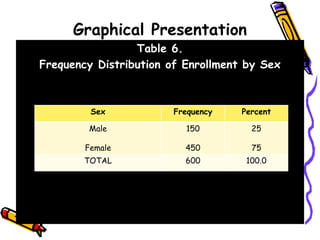
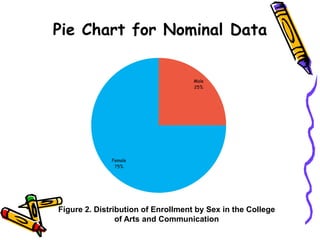
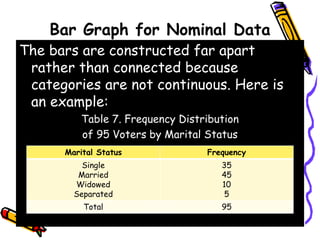
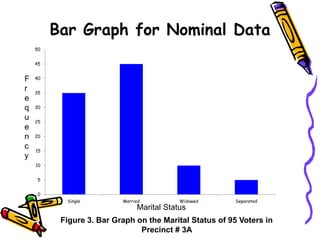
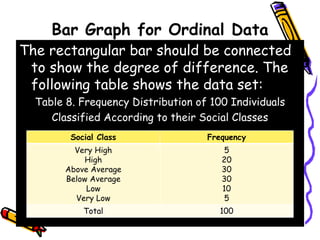
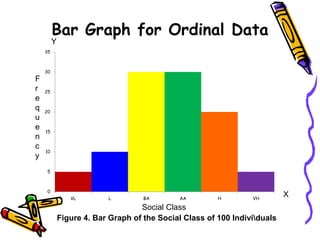
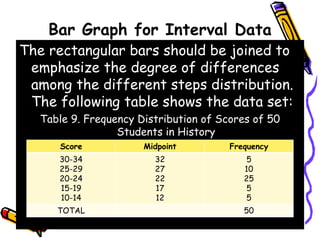
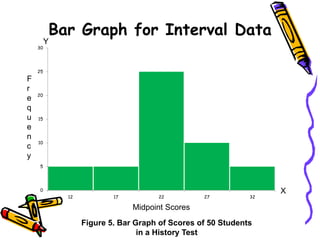
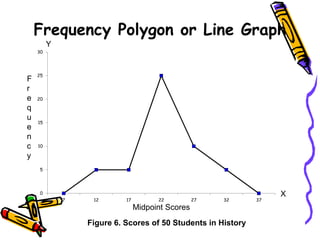
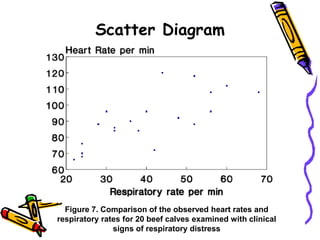
The document discusses methods and principles of data presentation, including definitions of key terms like 'data' and 'presentation'. It categorizes data into primary, secondary, qualitative, and quantitative types, and outlines various levels of measurement such as nominal, ordinal, interval, and ratio. Additionally, it highlights guidelines for effective data presentation and different formats including tabular and graphical methods, with examples demonstrated throughout.

1. “Data”,
Anyone?
EDUC 211: EDUCATIONAL STATISTICS
Sources: Statistics Made Simple
by Antonio S. Broto and
http://www.caribvet.net/

2. Outline
 Introduction
 Some Rules in Data Presentation
 Types of Data Presentation
Tabular Presentation
Graphical Presentation
References

5. Source: http://www.census.gov.ph

6. Source: http://www.census.gov.ph

7. IN MATH AND STATISTICS,
NUMBERS SPEAK LOUDER THAN
WORDS...
BUT CHARTS AND GRAPHS
SPEAK LOUDER THAN NUMBERS!

8. Introduction
 First Things First
 Define “Presentation” and “Data”

9. Introduction
 “Presentation”
- act of presenting something:
an act of presenting something
or the state of being presented
(Source: Microsoft® Encarta® 2009. ©
1993-2008 Microsoft Corporation. All
rights reserved.)

10. Introduction
 “Data” (plural of datum)
- item of information: a piece of
information
- factual information: information, often in
the form of facts or figures obtained from
experiments or surveys, used as a basis for
making calculations or drawing conclusions
(Source: Microsoft® Encarta® 2009. ©
1993-2008 Microsoft Corporation. All
rights reserved.)

11. Introduction
 “Data” (plural of datum)
- Point to statistical facts, principles,
opinions and various items of different
sources.
- (Source: Broto, Antonio S. 2006.
Statistics Made Simple. National Book
Store: Mandaluyong City.)

12. Introduction
 “Data” (plural of datum)
- a set of values of qualitative or quantitative
variables
- In Statistics, data are usually presented in
tabular form as numbers or values of variables
representing certain concepts
- Raw data, i.e., unprocessed data, refers to a
collection of numbers and characters
- (Source: Wikipedia.org)

13. Introduction
 Types of Data
1. Primary Data
2. Secondary Data

14. Introduction
 Primary Data
- The data, which are collected from the units or
individual respondents directly for the purpose of
certain study or information, are known as primary
data. For instance, an enquiry is made from each
tax payer in a city to obtain their opinion about the
tax collecting machinery. The data obtained in a
census study are termed as primary data.

15. Introduction
 Secondary Data
- The data, which had been collected by certain
people or agency, and statistically treated and now
the information contained in it is used again from
records, processed and statistically analysed to
extract some information for other purpose, is
termed as secondary data. For instance, if the data
given in different census years is again processed
to obtain trends of population growth, professional
changes, changes in sex ratio, mortality rate etc., it
is termed as secondary data. Usually, secondary
data is obtained from year books, census reports,

16. Introduction
 Secondary Data
Survey reports, official records or reported
experimental findings. Different organisations and
government agencies publish information (data) in
the form of reports, periodicals, journals etc.
(Source: Agarwal, B. L. 2006. Basic Statistics.
Revised Fourth Edition. New Age International (P)
Ltd.: New Delhi.)

17. Introduction
 Another Types of Data
1. Qualitative Data
2. Quantitative Data

18. Introduction
 Another Types of Data
1. Qualitative Data
 Deals with descriptions.
 Data can be observed but not measured.
 Colors, textures, smells, tastes, appearance,
beauty, etc.
 Qualitative → Quality
(Source: http://www.regentsprep.org)

19. Introduction
 Another Types of Data
2. Quantitative Data
 Deals with numbers.
 Data which can be measured.
 Length, height, area, volume, weight, speed,
time, temperature, humidity, sound levels, cost,
members, ages, etc.
 Quantitative → Quantity
(Source: http://www.regentsprep.org)

23. Introduction
 Levels or Scales of Measurement of Data
1. Nominal
2. Ordinal
3. Interval
4. Ratio

24. Introduction
 Levels or Scales of Measurement of Data
1. Nominal
 The name 'Nominal' comes from the
Latin nomen, meaning 'name' and nominal data
are items which are differentiated by a simple
naming system.
 The only thing a nominal scale does is to say
that items being measured have something in
common, although this may not be described.

25. Introduction
 Levels or Scales of Measurement of Data
1. Nominal
 Nominal items may have numbers assigned to
them. This may appear ordinal but is not -- these
are used to simplify capture and referencing.
 Nominal items are usually categorical, in that
they belong to a definable category, such as
'employees'.

26. Introduction
 Levels or Scales of Measurement of Data
1. Nominal
 Example
The number pinned on a sports person.
A set of countries.

27. Introduction
 Levels or Scales of Measurement of Data
2. Ordinal
 Items on an ordinal scale are set into some kind
of order by their position on the scale. This may
indicate such as temporal position, superiority,
etc.
 The order of items is often defined by assigning
numbers to them to show their relative position.
Letters or other sequential symbols may also be
used as appropriate.

28. Introduction
 Levels or Scales of Measurement of Data
2. Ordinal
 Ordinal items are usually categorical, in that they
belong to a definable category, such as '1956
marathon runners'.
 You cannot do arithmetic with ordinal numbers --
they show sequence only.

29. Introduction
 Levels or Scales of Measurement of Data
2. Ordinal
 Example
The first, third and fifth person in a race.
Pay bands in an organization, as denoted by A, B,
C and D.

30. Introduction
 Levels or Scales of Measurement of Data
3. Interval
 Interval data (also sometimes called integer) is
measured along a scale in which each position
is equidistant from one another. This allows for
the distance between two pairs to be equivalent
in some way.
 This is often used in psychological experiments
that measure attributes along an arbitrary scale
between two extremes.
 Interval data cannot be multiplied or divided.

31. Introduction
 Levels or Scales of Measurement of Data
3. Interval
 Example
My level of happiness, rated from 1 to 10.
Temperature, in degrees Fahrenheit.

32. Introduction
 Levels or Scales of Measurement of Data
4. Ratio
 In a ratio scale, numbers can be compared as
multiples of one another. Thus one person can
be twice as tall as another person. Important
also, the number zero has meaning.
 Thus the difference between a person of 35 and
a person 38 is the same as the difference
between people who are 12 and 15. A person
can also have an age of zero.

33. Introduction
 Levels or Scales of Measurement of Data
4. Ratio
 Ratio data can be multiplied and divided
because not only is the difference between 1
and 2 the same as between 3 and 4, but also
that 4 is twice as much as 2.
 Interval and ratio data measure quantities and
hence are quantitative. Because they can be
measured on a scale, they are also called scale
data.

34. Introduction
 Levels or Scales of Measurement of Data
4. Ratio
 The ratio type takes its name from the fact that
measurement is the estimation of the ratio
between a magnitude of a continuous quantity
and a unit magnitude of the same kind. A ratio
scale possesses a meaningful (unique and non-
arbitrary) zero value. Most measurement in the
physical sciences and engineering is done on
ratio scales. Examples include mass, length,
duration, plane angle, energy and electric
charge.

35. Introduction
 Levels or Scales of Measurement of Data
4. Ratio
 Example
A person's weight
The number of pizzas I can eat before fainting
(Sources: http://changingminds.org and
Wikipedia.org)

36. Source: http://www.census.gov.ph
Sample Data Set

37. Introduction
 In most cases, the data collected from the
different sources through various methods
of data collection are generally raw,
unorganized and haphazard. To give
meaning to these raw data, appropriate
tables and graphs are used. Here, we will
consider tabular presentation through
frequency distribution and the different
methods of graphical presentation.

38. Introduction
 The presentation of data in the form of
tables, graphs and charts is an important
part of the process of data analysis and
report writing. Although results can be
expressed within the text of a report, data
are usually more digestible if they are
presented in the form of a table or
graphical display.

39. Introduction
 In Research, the presentation of data is a
usual part of the last section of the
research proposal and research paper.
The common parts of a research paper
are the following:
1. The Research Problem
2. Review of Related Literature
3. Research Methodology
4. Presentation, Analysis and
Interpretation of Data

40. Introduction
 The Presentation, Analysis and
Presentation of Data section of the
research paper includes the Data
Processing and Data Analysis.
 The Data Processing part is where the
researcher presents the processed data
that are usually presented in tables and
graphs.

41. Introduction
 Graphs and charts can quickly convey to
the reader the essential points or trends in
the data. Graphs and charts are
particularly useful when data are being
presented to an audience, because
information has to be conveyed in a limited
time period.

42. Introduction
 Graphs and charts can, however, be
misleading especially if the author uses
subtle alterations of scale such as
excluding a 0 reference point on one of the
axes.

43. Some Rules in Data Presentation
1. The presentation should be as
simple as possible.
2. The presentation should be self-
explanatory.
3. The title should be clear, and
concise indicating what?, when?,
and where? the data were obtained.

44. Some Rules in Data Presentation
4. Codes, legends and labels should
be clear and concise, following
standard formats if possible.
5. The use of footnotes is advised to
explain essential features of the
data that are critical for the correct
interpretation of the graph or chart.

45. Types of Data Presentation
 Tabular Presentation
 Frequency Distribution
 Graphical Presentation
 Pie Chart for Nominal Data
 Bar Graph for Nominal Data
 Bar Graph for Ordinal Data
 Bar Graph for Interval Data
 Frequency Polygon or Line Graph
 Scatter Diagram

46. Tabular Presentation
• Tables are a standard method of
presenting qualitative or categorical
data, but they can also be used to
summarize quantitative data
• The simplest table is the two-column
frequency table. The first column
indicates the grouping of the data, while
the second column lists the frequencies
or count for each group.

47. Frequency Distribution
Example 1: Suppose a mathematics
class with 30 students is given an
examination and the raw scores are
shown in the following Table.
Table 2.
_____Test Scores Obtained by the Students in Mathematics_____
48 73 57 50 78 47
79 70 45 65 38 59
30 59 60 55 65 68
32 49 71 35 66 58
32 36 68 59 59 50

48. Frequency Distribution
Table 3.
Frequency Distribution of the Examination Results
of Thirty Students in Mathematics
Scores Tally Frequency Percent
70-79
60-69
50-59
40-49
30-39
lllll
lllll-l
lllll-llll
llll
lllll-l
5
6
9
4
6
16.7
20.0
30.0
13.3
20.0
Total 30 100.0

49. Frequency Distribution
Table 4.
Frequency Distribution of the Thirty Students
Grouped According to their Respective Courses
Courses Frequency Percent
AB Journalism
AB Broadcasting
AB Political Science
AB Sociology
5
8
10
7
16.7
26.7
33.3
23.3
TOTAL 30 100.0

50. Frequency Distribution
Table 5.
Frequency Distribution of Thirty Students
According to Sex
Sex Frequency Percent
Male
Female
13
17
43.3
56.7
TOTAL 30 100.0

51. Graphical Presentation
The data can be presented graphically
according to their scales or levels of
measurement. The most common graphic
presentations are the pie chart or circle
graph, histogram or bar graph and
frequency polygon or line graph.

52. Graphical Presentation
Graphs are a useful method to display
quantitative data. The standard graph
uses two rectangular co-ordinates
(called the x and y axes). The
independent variable is usually plotted
on the horizontal x axis, while the
response or outcome variable is plotted
on the vertical y axis.

53. Graphical Presentation
The outcome variable is usually a
quantitative measure such as a
frequency (count) or a percentage.

54. Graphical Presentation
Table 6.
Frequency Distribution of Enrollment by Sex
Sex Frequency Percent
Male
Female
150
450
25
75
TOTAL 600 100.0

55. Pie Chart for Nominal Data
The pie chart or circle graph can provide
an easy presentation of nominal data or
any categorical data. The whole circular
graph equals 100%. Likewise one
complete revolution equals 360°. So in
making the graph, multiply the 360° by
the percentage in every category.
Example: 25% of 360° = 90°
75% of 360° = 90°

56. Pie Chart for Nominal Data
Male
25%
Female
75%
Figure 2. Distribution of Enrollment by Sex in the College
of Arts and Communication

57. Bar Graph for Nominal Data
The bars are constructed far apart
rather than connected because
categories are not continuous. Here is
an example:
Table 7. Frequency Distribution
of 95 Voters by Marital Status
Marital Status Frequency
Single
Married
Widowed
Separated
35
45
10
5
Total 95

58. Bar Graph for Nominal Data
Figure 3. Bar Graph on the Marital Status of 95 Voters in
Precinct # 3A
0
5
10
15
20
25
30
35
40
45
50
Single Married Widowed Separated
Marital Status
F
r
e
q
u
e
n
c
y

59. Bar Graph for Ordinal Data
The rectangular bar should be connected
to show the degree of difference. The
following table shows the data set:
Table 8. Frequency Distribution of 100 Individuals
Classified According to their Social Classes
Social Class Frequency
Very High
High
Above Average
Below Average
Low
Very Low
5
20
30
30
10
5
Total 100

60. Bar Graph for Ordinal Data
Figure 4. Bar Graph of the Social Class of 100 Individuals
0
5
10
15
20
25
30
35
VL L BA AA H VH
F
r
e
q
u
e
n
c
y
Social Class
Y
X

61. Bar Graph for Interval Data
The rectangular bars should be joined to
emphasize the degree of differences
among the different steps distribution.
The following table shows the data set:
Table 9. Frequency Distribution of Scores of 50
Students in History
Score Midpoint Frequency
30-34
25-29
20-24
15-19
10-14
32
27
22
17
12
5
10
25
5
5
TOTAL 50

62. Bar Graph for Interval Data
Figure 5. Bar Graph of Scores of 50 Students
in a History Test
0
5
10
15
20
25
30
12 17 22 27 32
F
r
e
q
u
e
n
c
y
Midpoint Scores
Y
X

63. Frequency Polygon or Line Graph
The frequency polygon is prepared by
making a histogram, plotting the points
using the frequency and the midpoints,
and connecting the points by straight
lines. This kind of presentation can also
be applied to ordinal or interval data
because it stresses continuity along a
scale. For example, the scores of 50
students in a history test are grouped
into a 5-step distribution.

64. Frequency Polygon or Line Graph
Figure 6. Scores of 50 Students in History
F
r
e
q
u
e
n
c
y
Midpoint Scores
0
5
10
15
20
25
30
7 12 17 22 27 32 37
Y
X

65. Scatter Diagram
This graph is extremely useful to explore
the relationship or association between
two continuous variables. Several sets
of paired data are plotted on the graph
and the resulting pattern of points is
indicative of a possible relationship.

66. Scatter Diagram
For example, during the clinical
examination of a number of beef calves
suffering from viral pneumonia the
heart rate and respiratory rate were
recorded for each calf. The following
scatter diagram indicates that there
seems to be some sort of relationship
between the two variables.

67. Scatter Diagram
Figure 7. Comparison of the observed heart rates and
respiratory rates for 20 beef calves examined with clinical
signs of respiratory distress

68. Agarwal, B. L. 2006. Basic Statistics. Revised Fourth
Edition. New Age International (P) Ltd.: New
Delhi.
Broto, Antonio S. 2006. Statistics Made Simple.
National Book Store: Mandaluyong City.
Microsoft® Encarta® 2009. © 1993-2008 Microsoft
Corporation. All rights reserved.
Pennings, Paul, Keman, Hans, and Kleinnijenhuis, Jan
1999. Doing Research in Political Science: An
Introduction to Comparative Methods and
Statistics. Sage: London.
References: