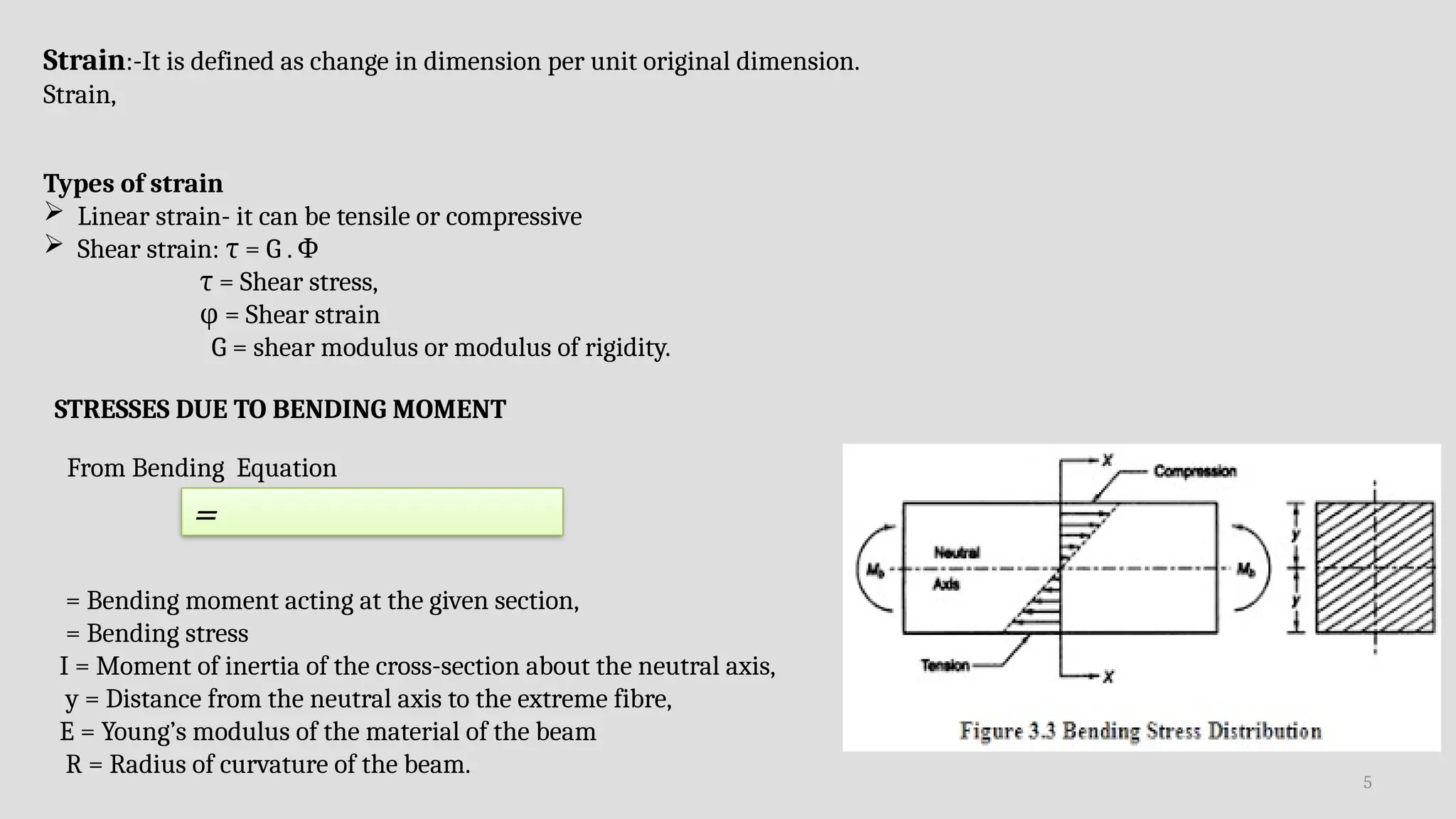
The document discusses various types of loads, stress, and strain in mechanical components, including static, dynamic, and impact loads, as well as their effects on material behavior. It covers concepts such as strain energy, factor of safety, fatigue loading, and stress concentration due to notches. Additionally, it details methods for evaluating material toughness, including Charpy and Izod impact tests, as well as the relationship between endurance limits and material properties.

1. Contents
Load and Types of load
Strain Energy
Charpy and Izod impact test
Factor of safety
Fatigue Loading
Endurance limit and SN Curve
Notches and Stress Concentrations
Combined mean and variable stress

2. LOAD
Load refers to the force or weight applied to
a structure or material. It can be a static
load (constant force) or a dynamic load
(changing force).
1

3. Types of Loading
(with respect to cross section on which load is acting)
Normal load
(load acting perpendicular to cross
section of plane)
Axial load
(line of action of load
passes through CG)
Tensile Load
Compressive
load
Eccentric Axial load
(line of action of load passes
away from CG)
Eccentric
tensile load
Eccentric
compressive load
Shear load
(Load acting Parallel along the cross
section)
Direct shear load
Eccentric Shear
load

4. Eccentric Loading
Stress And Strain
 Direct stresses can be tensile or compressive.
 Shear Stress- It is due to shear force.
Shear stress,
The load whose line of action do not passes through the C.G, it
passes at some distance from CG, then it is called Eccentric
Loading.
Stress-The internal resisting force per unit area of the
component is called stress.
Stress,

5. 5
Strain:-It is defined as change in dimension per unit original dimension.
Strain,
Types of strain
 Linear strain- it can be tensile or compressive
 Shear strain: =
τ G . Φ
= Shear stress,
τ
= Shear strain
φ
G = shear modulus or modulus of rigidity.
STRESSES DUE TO BENDING MOMENT
=
= Bending moment acting at the given section,
= Bending stress
I = Moment of inertia of the cross-section about the neutral axis,
y = Distance from the neutral axis to the extreme fibre,
E = Young’s modulus of the material of the beam
R = Radius of curvature of the beam.
From Bending Equation

6. STRESSES DUE TO TORSIONAL MOMENT
From torsion equation
𝑀𝑡
𝐽
=
𝜏
𝑟
=
𝐺 𝜃
𝑙
Torsional shear stress,
= Torsional shear stress induced at the outer surface of the shaft or maximum shear stress,
τ
r = Radius of the shaft,
T or = Torque or twisting moment,
J = Second moment of area of the section about its polar axis or polar moment of inertia,
G= Modulus of rigidity for the shaft material,
l = Length of the shaft,
= Angle of twist in radians on a length l
θ
𝜏=
𝑀𝑡 𝑟
𝐽

7. Static
Load
• Gradually Applied Load
•
Dynamic
Load
• Suddenly Applied Load
• Impact Load
• Fatigue Load
Types of Loading
(with respect to time)

8. • GRADUALLY APPLIED LOAD
A static load is defined as a force, which is gradually applied to a
mechanical component and which does not change its magnitude or
direction with respect to time.
1)STATIC LOAD
In this loading will starts from zero magnitude and increases gradually till
the body is fully loaded.
GRADUALLY APPLIED LOAD

9. Suddenly applied load
In this loading, the whole magnitude of the load is applied suddenly on a body.
 An example would be placing a heavy weight quickly on a beam.
Impact load
The load which is applied with some velocity (or which are fall from a height)
on a body is known as impact or shock load.
 An example would be include a hammer strike or a falling object hitting a
surface.
Fatigue load
A load which is applied repeatedly or cyclically over time lead to failure of
material.
 Common fatigue failure are in transmission shafts, connecting rods, gears,
vehicle suspension springs and ball bearings.
Dynamic Load is a load whose magnitude or direction or both magnitude and
direction changes with respect to time.
1)DYNAMIC LOAD

10. 10
Strain Energy- The energy absorbed by the body when work is done on it in straining(deforming) within
elastic limit. i.e.
Strain energy of body = Work done by the body
It is represented by U.
Resilience: The total strain energy stored by the body within the elastic limit when loaded externally is called
resilience.
Proof resilience: The maximum strain energy which can be stored in a body up to the elastic limit is called
proof resilience.
Modulus of resilience: Proof resilience per unit volume the body is known as modulus od resilience.
Strain Energy
Modulus of Resilience=
Proof Resilience
Volume of the body

11. Let P be the gradually load applied on a body and δl be the corresponding change in length.
Since the load applied is gradual, and varies from zero to P
So Work done by the body = Force × Distance
= Average load ×Deformation
=
== (δl=ε×l)
= (P=σ×A, ε=σE)
=
Work done by the body
But, strain energy of body = Work done by the body
So Strain energy stored by the body, U=W=
Also, Modulus of resilience = Strain energy per unit volume
=
I) Gradually applied load
Strain Energy and Stress for different types of Loading

12. 2)suddenly Applied Load
Let P be the load applied suddenly on a body and let be the
δ𝑙
corresponding change in length. Since the load is applied
suddenly.
∴ Work done = Force × Distance
= Load × Deformation
= ×
𝑃 𝛿
𝑙
= × / ×l
𝑃 𝐸
𝜎
But, strain energy of body = Work done by the body

13. So,Stress for suddenly applied load,
i.e. Stress due to suddenly applied load is double to that of gradually applied load.
𝜎 𝑠 =2 𝜎 𝑔

14. 3) Impact load or shock load
The load which is applied with some velocity (or which are fall from a height) on a body is known as
impact or shock load.
Consider a weight P falling through a height h on a collar fitted on the
rod which is of length l and has cross-section area A producing an
instantaneous elongation in the bar.
𝛿
𝑙
Loss of potential energy of weight = Work done by weight on the bar
= Load × Distance moved
= ( + )
𝑃 ℎ 𝛿
𝑙
Since, Strain energy stored = the work done

15. Since , Strain energy stored = the work done
=
=
=
Solving the quadratic equation we get,
If is negligible as compared to h,
Impact load,

16. Charpy and Izod impact Test
The Charpy and Izod impact tests are both standardized
methods to determine the impact strength or toughness of
materials.

17. FACTOR OF SAFETY
While designing a component, it is necessary to provide sufficient reserve strength in
case of an accident. This is achieved by taking a suitable factor of safety
Factor of safety() =
For ductile materials, For brittle materials,
 and are the yield strength and the ultimate tensile strength of the material respectively.

18. 1)Completely reversed stresses:-
It also fluctuates between two limits maximum ( max) &
𝜎
minimum (−𝜎min) stress. For completely reversed stresses as
shown in fig. 𝜎min = −𝜎max.
= =0
Mean stress, =

19. 2)Repeated stresses:-
It also fluctuates between two limits maximum (𝜎max) &
minimum (𝜎min = 0) stress.
Mean stress, =
Stress Amplitude,=

20. ENDURANCE LIMIT
The fatigue or endurance limit of a material is defined as the maximum amplitude of
completely reversed stress that the standard specimen can withstand for an infinite number
of cycles without fatigue failure. It is represented by
Endurance Strength(Fatigue Strength) - It may be defined as the safe maximum stress
which can be applied to the machine part working under actual conditions. It is
represented by
To determine the endurance limit of a material, a
number of tests are to be carried out by means of
a rotating beam machine developed by R R
Moore.

21. The results of these tests are plotted by means of an S–N curve.
The S–N curve is the graphical representation of stress amplitude ( ) versus the number of
stress cycles (N) before the fatigue failure.

22. Relation Between Endurance Limit() and Ultimate Tensile Strength(
There is an approximate relationship between the endurance limit () and
the ultimate tensile strength () of the material.
o For steels, = 0.5
o For cast iron and cast steels, = 0.4
o For Wrought Aluminium alloys, = 0.4
o For Cast aluminium alloys = 0.3
Factor of Safety for Fatigue Loading
When a component is subjected to fatigue loading, the endurance limit is the criterion for failure.
Factor of safety() =

23. Endurance limit stress of a particular mechanical component depends
upon Various Factors
 Loading Factors ()
 Environmental Factors such as Temperature()
 Reliability Factors ()
 Size Effects ()
 Corrected Surface Effects ()
Se’= endurance limit stress of a rotating beam specimen subjected to reversed bending stress (N/mm2)
= endurance limit stress of a particular mechanical component subjected to reversed bending stress
(N/mm2)
𝑆𝑒=𝐶𝑙𝑜𝑎𝑑 𝐶𝑠𝑢𝑟𝑓 𝐶𝑠𝑖𝑧𝑒 𝐶𝑡𝑒𝑚𝑝 𝐶𝑟𝑒𝑙𝑖𝑎𝑏 𝑆𝑒′

24. Loading Factor
The endurance limit will also be different for different types of loading. So this factor
varies with the loading type viz., reversed axial load, reversed bending ,etc.
i.e.
For reversed or rotating Bending load, = 1
For reversed axial load, = 0.7
For reversed torsional or shear load,
Size Factor ()
A large size specimen will have more defects than a small one. So, as size increases, this factor reduces.
 The value of for different range of diameter of specimen is given as follows:

25. o For axial loading case = 1 as the failure in axial loading is independent of cross sectional
area
o For d <= 8 mm, = 1
o For 8 mm < d <= 250 mm, =
o For d > 250 mm, = 0.6
The above equations are valid for steels. For non-ferrous metals, the equations are not precise.
Surface Factor ()
 Rough surface reduces fatigue strength
For cast iron =1 as their internal discontinuities dominate the surface finish effects
 Electroplating the surface with metals drastically reduces the fatigue strength
Shigley and Mischke have suggested an exponential equation for the surface finish factor.
Surface Factor () = A(Sut) if > 1.0, set = 1.0

26. Temperature Factor ()
 Fatigue tests are done at room temperature
 Correction should be made for the service conditions
o For T <= 450° C, = 1
o 450°C <T< 550°C, = 1-0.0058(T-450)
o The above criteria is based on steels and hence not valid for other metal.
Reliability Factor () Modifying factor for stress concentration
The modifying factor to account for the effect of stress
concentration is defined as
=

27. Notches and Stress Concentrations
Stress Concentration
Stress concentration is defined as the localization or concentration of high stresses due to the
irregularities present in the component and abrupt changes of the cross section.
Q. What is a notch?
 a hole
 a groove
 a fillet
 an abrupt change in cross section
 any disruption to the smooth contours of a part
 fastener holes, key holes on shafts, O-ring grooves etc.

28. 28
Theoretical or Form Stress Concentration Factor()
To consider the effect of stress concentration and find out localized stresses, a factor called stress
concentration factor is used. It is denoted by
Stress Concentration due to Holes and Notches
Stress Concentration due to Elliptical Hole is given by
For circular hole, a = b
= 3

29. Fatigue Stress Concentration Factor()
In case dynamic loading the value of fatigue stress concentration factor shall be applied instead of
theoretical stress concentration factor.
Notch sensitivity
Notch sensitivity is defined as the susceptibility of a material to succumb to the damaging effects of
stress raising notches in fatigue loading.
​can be larger than​)
Because of the specific conditions of loading and crack geometry, which lead to higher stress
concentrations at the crack tip.

30. 30
30
 When the material has no sensitivity to notches,
q = 0 and = 1
 When the material is fully sensitive to notches,
q = 1 =
Causes of Stress Concentration
Methods of Reducing or avoiding stress concentration
 Ductile materials are less notch sensitive, brittle material are more notch sensitive
 Reduction of notch radius decreases notch sensitivity
 Geometric discontinuities like cracks, sharp corners, holes,
abrupt cross-sectional changes etc.
 Discontinuity in applied loads.
 poor surface finish.
 localized loading.
 Variation in material properties.
 Avoid Abrupt change in cross section.
 If a crack is present then drill a large hole at the end of the
crack.
 If already a notch is there then make more notches for
uniform strength.
 By improving surface finish.

31. Combined mean and variable stress
= limiting safe stress amplitude
= endurance limit of the component
= limiting safe mean stress
= ultimate tensile strength
= Yield strength
N = Factor of safety
When a component is subjected to fluctuating stresses, there is mean stress () as well as stress amplitude ().
The fatigue diagram for this general case are:

32. Soderberg Line
The line joining (yield strength of the material) on the mean stress axis and (endurance limit of the component) on stress
amplitude axis is called as Soderberg line.
This line is used when yielding defines failure ( For Ductile materials).
Gerber Line
A parabolic curve joining (endurance limit of the component ) on the stress amplitude axis to (ultimate tensile strength) on
the mean stress axis is called the Gerber line.
The equation for the Gerber line:

33. Goodman Line
The line joining on the stress amplitude axis and on the mean stress axis is known as the Goodman line.
The triangular region below this line is considered a safe region.