第116回音楽情報科学研究会 MMアルゴリズムの説明を追加しました． English title: Nonnegative Matrix Factorization Based on Complex Laplace Distribution Authors: H. Tanji, T. Murakami, H. Kamata Institution: Meiji University Presented in IPSJ Music and Computer 116th Domestic Workshop, Aug. 2017. Detail of MM algorithm for Laplace-NMF is added to the presented slide.

1. 複素ラプラス分布に基づく
非負値行列因子分解
丹治寛樹，村上隆啓，鎌田弘之（明治大学）
2017/08/24
第 116 回音楽情報科学研究会（夏のシンポジウム）

2. 目次
(1) 非負値行列因子分解（NMF）
音響信号への適用
評価関数
(2) 複素スペクトルの統計モデル
複素スペクトルの従う分布
分散の統計モデル
(3) 提案法 複素ラプラス分布に基づく NMF
統計モデル
最適化アルゴリズム
(4) シミュレーション
多重音の分解
(5) まとめ
1 / 17

3. 研究背景
非負値行列因子分解
Nonnegative matrix factorization; NMF [Lee(1999)]
• 非負行列（すべての要素が負ではない行列）から
頻出パターンを抜き出すための枠組み
• 振幅 or パワースペクトログラムに適用すれば，
個々の音源のスペクトルとアクティベーションに
分解できる [Smaragdis(2003)]
スペクトログラム Y
Time
Frequency
スペクトル W アクティベーション H
Frequency
Time
分解
2 / 17

4. NMFの定式化
一般的なモデル
Y W
H
ˆY=
観測データ [ymn] 基底 [wmk] 重み [hkn] 推定値 [ˆymn]
振幅 or パワースペクトルの加法性 いずれかを仮定
Y ˆY1
ˆY2 + · · ·+
観測信号の振幅 音源 1 の振幅 音源 2 の振幅
観測信号のパワー 音源 1 のパワー 音源 2 のパワー
3 / 17

5. NMFの定式化
一般的なモデル
Y W
H
ˆY=
観測データ [ymn] 基底 [wmk] 重み [hkn] 推定値 [ˆymn]
Y と ˆY の乖離度を考慮
評価関数の最小化問題
F(W , H) =
m,n
f(ymn; ˆymn)
Y の統計的な生成過程を考慮
尤度関数の最大化問題
p(Y ; ˆY ) =
m,n
p(ymn; ˆymn)
評価関数 or 尤度関数をどう設定するか
4 / 17

6. NMFの評価関数・尤度関数
• ユークリッド距離の二乗：Eu–NMF [Lee(1999)]
NMF の歴史の始まり
• Kullback–Leibler (KL) divergence：KL–NMF [Lee(1999)]
振幅スペクトルの分解に適用すれば，トップクラスの分離性能
信号分離における理論的な妥当性は不明
• Itakura–Saito (IS) divergence：IS–NMF [Fevotte(2008)]
複素正規分布の再生性に基づいて
パワースペクトルの加法性を正当化
• 複素コーシー分布：Cauchy–NMF [Liutkus(2015)]
複素コーシー分布の再生性に基づいて
振幅スペクトルの加法性を正当化
信号分離の性能は KL–NMF と “Competitive”
• 複素 t 分布：t–NMF [Yoshii(2016)]
IS–NMF と Cauchy–NMF の一般化
5 / 17

7. NMFの評価関数・尤度関数
複素分布を用いた観測信号のモデリング
• 観測信号の複素スペクトルをモデリング
• 分布の再生性があれば，
振幅 or パワースペクトルの加法性を正当化可能
• Itakura–Saito (IS) divergence：IS–NMF [Fevotte(2008)]
複素正規分布の再生性に基づいて
パワースペクトルの加法性を正当化
• 複素コーシー分布：Cauchy–NMF [Liutkus(2015)]
複素コーシー分布の再生性に基づいて
振幅スペクトルの加法性を正当化
信号分離の性能は KL–NMF と “Competitive”
• 複素 t 分布：t–NMF [Yoshii(2016)]
IS–NMF と Cauchy–NMF の一般化
5 / 17

8. 実環境の複素スペクトルが従う分布
-2.5
0.0
2.5
Real
010203040506070
Frequency [%]
-2.5
0.0
2.5
Imaginary
0 1 2 3 4 5
Frequency [kHz]
Figure 1: ピアノの 3 重音のスペクトル
音響信号の複素スペクトルは優ガウス性を持つ傾向 [Martin(2002)]
• 調波構造を持つスペクトルなら必ず優ガウス性
• 複素正規分布の分散をモデリングすることで
優ガウス性を表現できないだろうか
6 / 17

9. 複素スペクトルの統計モデル
IS-NMF [Fevotte(2008)]
複素スペクトル yC
mn は，
分散 ˆymn 複素正規分布から生成される
統計モデルの観点から拡張
複素正規分布の分散の分布を考慮して，
分散を周辺化
ˆymn yC
mn NC(0, ˆymn)
λmn zmn yC
mn ζmn
NC(0, zmnζmn)p(zmn; λmn)
ガンマ分布 G(z−1
mn; ν
2
, ν
2
)
0 5 10 15 20 25 30
z
0.0
0.5
1.0
1.5
2.0 nu = 2.0
nu = 5.0
nu = 10.0
nu = 50.0
ガンマ分布 G(zmn; 3
2
, λ−1
mn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.2
0.4
0.6
0.8
1.0
1.2 lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
指数分布 E(zmn; λmn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.5
1.0
1.5
2.0
lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
yC
mn の優ガウス性を仮定
7 / 17

10. 先行研究 t-NMF
t–NMF [Yoshii(2016)]
• 複素スペクトル ˆyC
mn が
自由度 ν の複素 t 分布に従うと仮定
裾の広い分布で複素スペクトルを表現
• パワースペクトルを分解
p(yC
mn; ˆymn) =
R+
NC(0, zmn ˆymn)G( ν
2
, ν
2
)dzmn
= TC(yC
mn; 0, ˆymn, ν)
zmn ν
yC
mn ˆymn
p(z−1
mn; ν)
= G(ν
2
, ν
2
)
NC(0, zmn ˆymn)
ガンマ分布 G(z−1
mn; ν
2
, ν
2
)
0 5 10 15 20 25 30
z
0.0
0.5
1.0
1.5
2.0 nu = 2.0
nu = 5.0
nu = 10.0
nu = 50.0
ガンマ分布 G(zmn; 3
2
, λ−1
mn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.2
0.4
0.6
0.8
1.0
1.2 lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
指数分布 E(zmn; λmn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.5
1.0
1.5
2.0
lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
8 / 17

11. 先行研究 IS-NMF
IS–NMF
• 複素スペクトル ˆyC
mn が尺度 ˆy2
mn の
球状ラプラス分布 [Kim(2007)] に従うと仮定
• 振幅スペクトルを IS divergence に基づいて分解
p(yC
mn; ˆymn) =
R+
NC(0, zmn)G( 3
2
, ˆy−2
mn)dzmn
= 2
ˆy2
mnπ
exp −
2|yC
mn|
ˆymn
zmn ˆymn
yC
mn
p(zmn; ˆymn)
= G( 3
2
, ˆy−2
mn)
NC(0, zmn ˆymn)
ガンマ分布 G(z−1
mn; ν
2
, ν
2
)
0 5 10 15 20 25 30
z
0.0
0.5
1.0
1.5
2.0 nu = 2.0
nu = 5.0
nu = 10.0
nu = 50.0
ガンマ分布 G(zmn; 3
2
, λ−1
mn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.2
0.4
0.6
0.8
1.0
1.2 lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
指数分布 E(zmn; λmn)
0.0 2.5 5.0 7.5 10.0 12.5 15.0
z
0.0
0.5
1.0
1.5
2.0
lambda = 0.5
lambda = 1.0
lambda = 2.0
lambda = 5.0
9 / 17

12. 提案法 複素ラプラス分布に基づくNMF
Laplace–NMF 厳密な優ガウス性を仮定
複素スペクトルが尺度 c2
ˆy2
mn の
複素ラプラス分布 [Lee(2008)] に従うと仮定
• 尤度関数は解析的に書けない
• 振幅 or パワースペクトルの加法性は
正当化されない
尤度関数
p(yC
mn; ˆymn) =
R+
NC(0, zmn)E(c2
ˆy2
mn)dzmn
=
2
c2 ˆy2
mnπ
K0
2|yC
mn|
cˆymn
Kν(t) 第二種変形ベッセル関数
zmn ˆymn
yC
mn
p(zmn; ˆymn)
= E(c2 ˆy2
mn)
NC(0, zmn ˆymn)
複素スペクトルのモデリングという観点で妥当
10 / 17

13. 提案法 複素ラプラス分布に基づくNMF
Laplace–NMF 厳密な優ガウス性を仮定
複素スペクトルが尺度 c2
ˆy2
mn の
複素ラプラス分布 [Lee(2008)] に従うと仮定
• 尤度関数は解析的に書けない
• 振幅 or パワースペクトルの加法性は
正当化されない
zmn ˆymn
yC
mn
p(zmn; ˆymn)
= E(c2 ˆy2
mn)
NC(0, zmn ˆymn)
評価関数 振幅スペクトルを分解する場合
ymn 振幅スペクトル
Kν(t) 第二種変形ベッセル関数
c 補正係数
F(W , H) =
m,n
2 log ˆymn − log K0
2ymn
cˆymn
MM アルゴリズム
評価関数 F の
上限 Q+
を最適化
˜ϑ ← arg min
ϑ
Q+
(W , H, ϑ)
W , H ← arg min
W ,H
Q+
(W , H, ˜ϑ)
上限 Q+ をどう作るか
11 / 17

14. 提案法 複素ラプラス分布に基づくNMF
Laplace–NMF 厳密な優ガウス性を仮定
複素スペクトルが尺度 c2
ˆy2
mn の
複素ラプラス分布 [Lee(2008)] に従うと仮定
• 尤度関数は解析的に書けない
• 振幅 or パワースペクトルの加法性は
正当化されない
zmn ˆymn
yC
mn
p(zmn; ˆymn)
= E(c2 ˆy2
mn)
NC(0, zmn ˆymn)
評価関数 振幅スペクトルを分解する場合
ymn 振幅スペクトル
Kν(t) 第二種変形ベッセル関数
c 補正係数
F(W , H) =
m,n
2 log ˆymn − log K0
2ymn
cˆymn
特殊関数
MM アルゴリズム
評価関数 F の
上限 Q+
を最適化
˜ϑ ← arg min
ϑ
Q+
(W , H, ϑ)
W , H ← arg min
W ,H
Q+
(W , H, ˜ϑ)
上限 Q+ をどう作るか
11 / 17

15. Laplace-NMFのMMアルゴリズム
F(W, H) =
m,n
2 log ˆymn − log K0
2ymn
cˆymn
Q+(W, H, ρ, ϕ)
Majorize
1 次の Taylor 展開（g：凹関数）
g(x) ≤ g (ϕ)(x − ϕ) + g(ϕ)
Jensen の不等式（f：凸関数）
f( k ρkxk) ≤ k ρkf(xk)
特殊関数に適用しても無意味
12 / 17

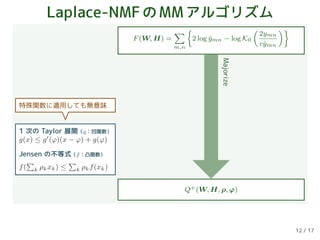
16. Laplace-NMFのMMアルゴリズム
F(W, H) =
m,n
2 log ˆymn − log K0
2ymn
cˆymn
Q+(W, H, ρ, ϕ)
Majorize
Q(W, H)=
m,n
2 log ˆymn +
Ep(zmn|ymn;˜ˆymn)[zmn]
c2 ˆy2
mn
Jensen の不等式（g：凹関数）
−g(E[x]) ≤ −E[g(x)]
1 次の Taylor 展開（g：凹関数）
g(x) ≤ g (ϕ)(x − ϕ) + g(ϕ)
Jensen の不等式（f：凸関数）
f( k ρkxk) ≤ k ρkf(xk)
EM アルゴリズムのアイデア
ˆymn についての
特殊関数が消える
Q(W , H) に適用
更新式の導出が可能な上限を設計できる
12 / 17

17. Laplace-NMFのMMアルゴリズム（追加）
評価関数の上限
F(W , H)
c
= −
m,n
log
R+
p(ymn|zmn)p(zmn; ˆymn)dzmn
= −
m,n
log
R+
p(zmn|ymn, ˜ˆymn)
p(ymn|zmn)p(zmn; ˆymn)
p(zmn|ymn, ˜ˆymn)
dzmn
≤ −
m,n R+
p(zmn|ymn, ˜ˆymn) log
p(ymn|zmn)p(zmn; ˆymn)
p(zmn|ymn, ˜ˆymn)
dzmn
Jensen の不等式（g：凹関数）
−g(E[x]) ≤ −E[g(x)]
13 / 17

18. Laplace-NMFのMMアルゴリズム（追加）
評価関数の上限
F(W , H)
c
= −
m,n
log
R+
p(ymn|zmn)p(zmn; ˆymn)dzmn
= −
m,n
log
R+
p(zmn|ymn, ˜ˆymn)
p(ymn|zmn)p(zmn; ˆymn)
p(zmn|ymn, ˜ˆymn)
dzmn
≤ −
m,n R+
p(zmn|ymn, ˜ˆymn) log
p(ymn|zmn) 指数分布
p(zmn|ymn, ˜ˆymn)
dzmn
c
=
m,n
2 log ˆymn +
Ep(zmn|ymn;˜ˆymn)[zmn]
c2 ˆy2
mn
= Q(W , H)
13 / 17

19. Laplace-NMFのMMアルゴリズム（追加）
更新アルゴリズム
振幅スペクトルの分解
評価関数 F(W , H) =
m,n
2 log ˆymn − log K0
2ymn
cˆymn
更新式 E
p(zmn|ymn;ˆy
(t)
mn)
[zmn] = cymn ˆy
(t)
mnK1
2ymn
cˆy
(t)
mn
K0
2ymn
cˆy
(t)
mn
w
(t+1)
mk = w
(t)
mk




n
E
p(zmn|ymn;ˆy
(t)
mn)
[zmn]
c2 ˆy
(t)
mn
3
h
(t)
kn
n
h
(t)
kn
ˆy
(t)
mn




1
3
h
(t+1)
kn = h
(t)
kn




m
E
p(zmn|ymn;ˆy
(t)
mn)
[zmn]
c2 ˆy
(t)
mn
3
w
(t)
mk
m
w
(t)
mk
ˆy
(t)
mn




1
3
14 / 17

20. シミュレーション
タスク 多重音を単音に分解する
比較対象 Eu-，KL-，IS-，Cauchy-，t-NMF
性能指標 Source-to-distortion ratio（SDR）[Vincent(2006)]
音源 ピアノ，エレキギター（RWC 音楽 DB 収録）
基底の数 K = 3 or 4
サンプリング周波数 11025Hz
フレーム長 512
フレーム周期 128
窓関数 Hamming 窓
FFT の長さ 1024
観測行列のサイズ 511×1202
初期値 乱数（100 通り）
G4
E4
C4
2s
K = 3 のピアノロール
B 4
G4
E4
C4
K = 4 のピアノロール
15 / 17

21. 結果
Laplace-NMF は既存の NMF と遜色ない性能 要追加検証
• 外れ値の個数は評価関数の最適解付近でのシャープさに依存
• 振幅ドメインの IS-NMF と結果が似る傾向
振幅ドメインの Laplace-NMF の方がより安定した分離が可能
-20
-10
0
10
20
(a)
Piano
SDR[dB]
K = 3
(b)
K = 4
Eu
(Amp.)
Eu
(Power)
KL
(Amp.)
KL
(Power)
IS
(Amp.)
IS
(Power)
Cauchy
t
(nu=2)
t
(nu=5)
Laplace
(Amp.)
Laplace
(Power)
-10
0
10
20
(c)
Electricguitar
SDR[dB]
Eu
(Amp.)
Eu
(Power)
KL
(Amp.)
KL
(Power)
IS
(Amp.)
IS
(Power)
Cauchy
t
(nu=2)
t
(nu=5)
Laplace
(Amp.)
Laplace
(Power)
(d)
Figure 2: SDR による評価結果 16 / 17

22. まとめと今後の課題
まとめ Laplace-NMF
モデル 複素ラプラス分布に基づく NMF
• 複素スペクトルの優ガウス性を考慮
• 評価関数は解析的に解けない
最適化 収束の保障されたアルゴリズムを導出
評価 音源分離を行えることを確認
今後の課題 信号分離に対する有効性の検証
• 初期値に依存
• 音源・タスクに依存
17 / 17

23. 参考文献 I
[Lee(1999)] D.D. Lee and H.S. Seung.
“Learning the parts of objects with nonnegative matrix factorization”.
Nature, 401, pp.788–791, Oct. 1999.
[Smaragdis(2003)] P. Smaragdis and J.C. Brown.
“Non-negative matrix factorization for polyphonic music transcription”.
In Proc. 2003 IEEE International Workshop on Applications of Signal Processing to
Audio and Acoustics (WASPAA), pp. 177–180, Oct. 2003.
[Fevotte(2008)] C. Fevotte, N. Bertin, and J. L. Durrieu.
“Nonnegative matrix factorization with the Itakura-Saito divergence: with
application to music analysis”.
Neural Computation, 21(3), pp.793–830, Sep. 2008.
[Liutkus(2015)] A. Liutkus, D. Fitzgerald, and R. Badeau.
“Cauchy nonnegative matrix factorization”.
In Proc. 2015 IEEE International Workshop on Applications of Signal Processing to
Audio and Acoustics (WASPAA), pp. 1–5, Oct. 2015.
[Yoshii(2016)] K. Yoshii, K. Itoyama, and M. Goto.
“Student’s T nonnegative matrix factorization and positive semidefinite tensor
factorization for single-channel audio source separation”.
In Proc. 2016 IEEE International Conference on Acoustics, Speech and Signal
Processing (ICASSP), pp. 51–55, Mar. 2016.

24. 参考文献 II
[Martin(2002)] R. Martin.
“Speech enhancement using MMSE short time spectral estimation with gamma
distributed speech priors”.
In Proc. 2002 IEEE International Conference on Acoustics, Speech and Signal
Processing (ICASSP), volume 1, pp. I–253–I–256, May 2002.
[Lee(2008)] B. Lee, T. Kaler, and R.W. Schafer.
“Maximum-likelihood sound source localization with a multivariate complex
Laplacian distribution”.
In Proc. 11th International Workshop on Acoustic Echo and Noise Control (IWAENC),
Sep. 2008.
[Vincent(2006)] E. Vincent, R. Gribonval, and C. Fevotte.
“Performance measurement in blind audio source separation”.
IEEE Trans. Audio, Speech, and Language Processing, 14(4), pp.1462–1469, Jul.
2006.