正規表現に潜む対称性　〜等式公理による等価性判定〜

Prologue
2
(a + b)⇤
(a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤
:

Prologue
2
(a + b)⇤
(a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤
:
:

(S) (M) (T)
(S) (M)
(T)
(M)
(M)
(T)
(T)
(M)
(T)
(a + b)⇤
⌘ (a⇤
b)⇤
a⇤
⌘ ((1 + aa⇤
)b)⇤
a⇤
⌘ (b + aa⇤
b)⇤
a⇤
⌘ b⇤
(aa⇤
bb⇤
)⇤
a⇤
⌘ (bb⇤
+ 1)(aa⇤
bb⇤
)⇤
a⇤
⌘ (bb⇤
(aa⇤
bb⇤
)⇤
+ (aa⇤
bb⇤
)⇤
)a⇤
⌘ (1 + bb⇤
(aa⇤
bb⇤
)⇤
+ aa⇤
bb⇤
(aa⇤
bb⇤
)⇤
)a⇤
⌘ (1 + (1 + aa⇤
)bb⇤
(aa⇤
bb⇤
)⇤
)a⇤
⌘ (1 + a⇤
bb⇤
(aa⇤
bb⇤
)⇤
)a⇤
⌘ a⇤
+ a⇤
bb⇤
(aa⇤
bb⇤
)⇤
a⇤
⌘ a⇤
+ a⇤
bb⇤
(aa⇤
bb⇤
)⇤
(1 + aa⇤
)
⌘ a⇤
+ a⇤
bb⇤
(aa⇤
bb⇤
)⇤
aa⇤
+ a⇤
bb⇤
(aa⇤
bb⇤
)⇤
⌘ a⇤
(1 + bb⇤
(aa⇤
bb⇤
)⇤
aa⇤
) + a⇤
bb⇤
(aa⇤
bb⇤
)⇤
⌘ a⇤
(bb⇤
aa⇤
)⇤
+ a⇤
bb⇤
(aa⇤
bb⇤
)⇤
⌘ (a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤
.
(T)
(M)
(S)
:

Resume
6
´ ´
I.
II.
III.
IV.
V. Conway

Author
Ryoma Sin’ya
( )
(Posdoc)
Oxford (Christ Church)
THE UNIVERSITY OF TOKYO

Author
Ryoma Sin’ya
( )
(Posdoc)
Oxford (Christ Church)
THE UNIVERSITY OF TOKYO
!
( )

Automata and Regular Expressions
I

Regular expressions
9
A
F
RegA
0 1
(concatenation) E · F EF
(sum) E + F,
(star) E⇤
.
a 2 A
E, F 2 RegA
( )

Interpretation
10
( )
E L(E)
L(0) = ; L(1) = {"} L(a) = {a}

Interpretation
10
( )
L(E + F) = L(E) [ L(F)
E L(E)
L(0) = ; L(1) = {"} L(a) = {a}

Interpretation
10
( )
L(E + F) = L(E) [ L(F)
E L(E)
L(EF) = L(E)L(F) = {uv | u 2 L(E), v 2 L(F)}
L(0) = ; L(1) = {"} L(a) = {a}

Interpretation
10
( )
L(E + F) = L(E) [ L(F)
L(E⇤
) = L(E)⇤
=
[
n 0
L(E)n
E L(E)
L(0) = ; L(1) = {"} L(a) = {a}

Interpretation
10
( )
L(E + F) = L(E) [ L(F)
L(E⇤
) = L(E)⇤
=
[
n 0
L(E)n
E L(E)
L(0) = ; L(1) = {"} L(a) = {a}
0
"

Equivalence of expressions
11
2 E F
E ⇡ F
E ⇡ F , L(E) = L(F).

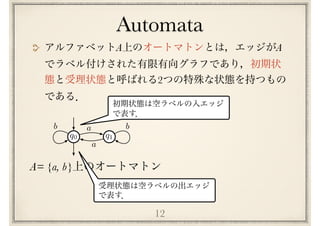
Automata
12
A A
2
q0 q1
a
a
b b
A= {a, b}

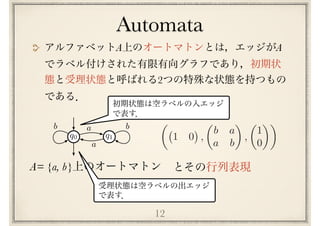
Automata
12
A A
2
q0 q1
a
a
b b
A= {a, b}
✓
1 0 ,
✓
b a
a b
◆
,
✓
1
0
◆◆

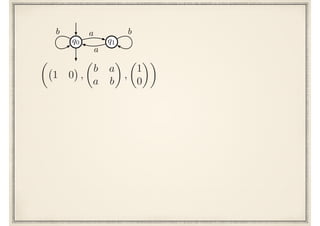
q0 q1
a
a
b b
✓
1 0 ,
✓
b a
a b
◆
,
✓
1
0
◆◆

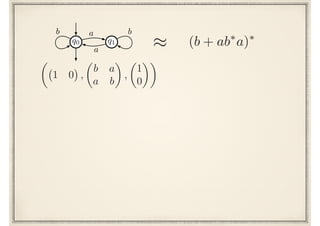
q0 q1
a
a
b b
⇡ (b + ab⇤
a)⇤
✓
1 0 ,
✓
b a
a b
◆
,
✓
1
0
◆◆

q0 q1
a
a
b b
⇡ (b + ab⇤
a)⇤
✓
1 0 ,
✓
b a
a b
◆
,
✓
1
0
◆◆
r0
r1
r2
r3
b a
a
b
a
b
a, b
0
B
B
@ 1 0 0 0 ,
0
B
B
@
a b 0 0
0 b a 0
a 0 0 b
0 0 0 a + b
1
C
C
A ,
0
B
B
@
0
0
0
1
1
C
C
A
1
C
C
A

q0 q1
a
a
b b
⇡ (b + ab⇤
a)⇤
✓
1 0 ,
✓
b a
a b
◆
,
✓
1
0
◆◆
⇡(a + b)⇤
bab(a + b)⇤
r0
r1
r2
r3
b a
a
b
a
b
a, b
0
B
B
@ 1 0 0 0 ,
0
B
B
@
a b 0 0
0 b a 0
a 0 0 b
0 0 0 a + b
1
C
C
A ,
0
B
B
@
0
0
0
1
1
C
C
A
1
C
C
A

Equivalence of automata
15
2
A ⇡ B , L(A) = L(B).
A ⇡ B
A B

Fundamental theorem
16
1951 Kleene
( )
定理
任意の⾔語について，次の条件は等しい．L
L
L
[Kleene51]
(1) はある正規表現の解釈．
(2) はあるオートマトンの振舞い．

18
[Kleene51]
lifetime by a relatively small mechanism.
The questions or reducibility of other mechanisms to
McCulloch-Pitts nerve nets (not always without increasing the
size of the mechanisms) is significant on this basis, but
trivial on the basis or explaining behavior over a fixed tiatt.
time only.
7. Regular Events:
7.1 "Regi:lar events" defined: We shall presently des-
cribe a class of events which we will call "regular events."
•'(We would welcome any suggest1lll'US as to a more descriptive term.
We assume for the purpose that the events refer to the
inputs up through time£ on a set of! input neurons Ni, ••• ,Nk
-the same for all events considered; but the definition
applies equally well for any k > 1 or even ror k • o.
- - -The events can refer to the value or £· Our objective
is to show that all and only regular events oan be represented
by nerve nets or finite automata. We have already seen in

18
[Kleene51]
lifetime by a relatively small mechanism.
The questions or reducibility of other mechanisms to
McCulloch-Pitts nerve nets (not always without increasing the
size of the mechanisms) is significant on this basis, but
trivial on the basis or explaining behavior over a fixed tiatt.
time only.
7. Regular Events:
7.1 "Regi:lar events" defined: We shall presently des-
cribe a class of events which we will call "regular events."
•'(We would welcome any suggest1lll'US as to a more descriptive term.
We assume for the purpose that the events refer to the
inputs up through time£ on a set of! input neurons Ni, ••• ,Nk
-the same for all events considered; but the definition
applies equally well for any k > 1 or even ror k • o.
- - -The events can refer to the value or £· Our objective
is to show that all and only regular events oan be represented
by nerve nets or finite automata. We have already seen in
“Regular”

From expressions to automata
19

From automata to expressions
20
0 1
E F H
G
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆

20
0 1
E F H
G
✓
E F
G H
◆⇤
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆

20
0 1
E F H
G
✓
E F
G H
◆⇤
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
2x2 star
( …)

20
0 1
E F H
G
✓
E F
G H
◆⇤ ✓
(E + FH⇤
G)⇤
E⇤
F(H + GE⇤
F)⇤
H⇤
G(E + FH⇤
G)⇤
(H + GE⇤
F)⇤
◆
=
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
2x2 star
( …)

20
0 1
E F H
G
✓
E F
G H
◆⇤ ✓
(E + FH⇤
G)⇤
E⇤
F(H + GE⇤
F)⇤
H⇤
G(E + FH⇤
G)⇤
(H + GE⇤
F)⇤
◆
=
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
C(A2) = I · M⇤
· T = (E + FH⇤
G)⇤2x2 star
( …)

20
0 1
E F H
G
✓
E F
G H
◆⇤ ✓
(E + FH⇤
G)⇤
E⇤
F(H + GE⇤
F)⇤
H⇤
G(E + FH⇤
G)⇤
(H + GE⇤
F)⇤
◆
=
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
C(A2) = I · M⇤
· T = (E + FH⇤
G)⇤
C(A2)A2
2x2 star
( …)

20
0 1
E F H
G
✓
E F
G H
◆⇤ ✓
(E + FH⇤
G)⇤
E⇤
F(H + GE⇤
F)⇤
H⇤
G(E + FH⇤
G)⇤
(H + GE⇤
F)⇤
◆
=
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
C(A2) = I · M⇤
· T = (E + FH⇤
G)⇤
C(A2)A2
star 2
2x2 star
( …)

20
0 1
E F H
G
✓
E F
G H
◆⇤ ✓
(E + FH⇤
G)⇤
E⇤
F(H + GE⇤
F)⇤
H⇤
G(E + FH⇤
G)⇤
(H + GE⇤
F)⇤
◆
=
A2 =
✓
I = 1 0 , M =
✓
E F
G H
◆
, T =
✓
1
0
◆◆
C(A2) = I · M⇤
· T = (E + FH⇤
G)⇤
C(A2)A2
star 2
Q: 3
2x2 star
( …)

21
M =
0
@
E F G
H I J
K L M
1
A

21
M =
0
@
E F G
H I J
K L M
1
A
3x3
2x2

21
M =
0
@
E F G
H I J
K L M
1
A =
✓
A B
C D
◆3x3
2x2

21
M =
0
@
E F G
H I J
K L M
1
A =
✓
A B
C D
◆
M⇤
=
✓
A B
C D
◆⇤
=
✓
(A + BD⇤
C)⇤
A⇤
B(D + CA⇤
B)⇤
D⇤
C(A + BD⇤
C)⇤
(D + CA⇤
B)⇤
◆
3x3
2x2

21
M =
0
@
E F G
H I J
K L M
1
A =
✓
A B
C D
◆
M⇤
=
✓
A B
C D
◆⇤
=
✓
(A + BD⇤
C)⇤
A⇤
B(D + CA⇤
B)⇤
D⇤
C(A + BD⇤
C)⇤
(D + CA⇤
B)⇤
◆
2x2
star 3
C(A)
3x3
2x2

21
M =
0
@
E F G
H I J
K L M
1
A =
✓
A B
C D
◆
M⇤
=
✓
A B
C D
◆⇤
=
✓
(A + BD⇤
C)⇤
A⇤
B(D + CA⇤
B)⇤
D⇤
C(A + BD⇤
C)⇤
(D + CA⇤
B)⇤
◆
2x2
star 3
C(A)
star
[Conway71]
3x3
2x2

Fundamental theorem
22
1951 Kleene
( )
定理
任意の⾔語について，次の条件は等しい．L
L
L
[Kleene51]
(1) はある正規表現の解釈．
(2) はあるオートマトンの振舞い．

Equivalence is decidable
23
( )
( )
A
A0
事実

23
( )
( )
A
A0
E
F
事実

23
( )
( )
A
A0
E
F
basic construction
AF
AE
事実

23
( )
( )
A
A0
E
F
basic construction
AF
AE
determinisation
& minimisation
A0
E
A0
F
事実

23
( )
( )
A
A0
E
F
basic construction
AF
AE
determinisation
& minimisation
A0
E
A0
F
compare
事実

23
( )
( )
A
A0
E
F
basic construction
AF
AE
determinisation
& minimisation
A0
E
A0
F
compare
E ⌘ F
A0
E = A0
F
,
事実

Summing up
24
( )
(PSPACE-complete!)

27
Kleene
Arto Salomaa 1966
[Salomaa66]
1
Redko [Redko64]
1971 John Conway
[Conway71] .
20 1991 Daniel Krob Conway
[Krob91].

The “Bible”
John Conway
[Conway71]

Trivial identities f
29
(T)
(E + F) + G ⌘ E + (F + G) (E · F) · G ⌘ E · (F · G)
(associativity)
E + F ⌘ F + E
(commutativity)
(unit elements)
E + 0 ⌘ 0 + E ⌘ E E · 1 ⌘ 1 · E ⌘ EE · 0 ⌘ 0 · E ⌘ 0
(distributivity)
E · (F + G) ⌘ E · F + E · G (E + (F) · G) ⌘ E · G + F · G

Trivial identities f
29
(T)
(E + F) + G ⌘ E + (F + G) (E · F) · G ⌘ E · (F · G)
(associativity)
E + F ⌘ F + E
(commutativity)
(unit elements)
E + 0 ⌘ 0 + E ⌘ E E · 1 ⌘ 1 · E ⌘ EE · 0 ⌘ 0 · E ⌘ 0
(distributivity)
E · (F + G) ⌘ E · F + E · G (E + (F) · G) ⌘ E · G + F · G
(semiring)
(T)
(RegA, 0, 1, +, ·).

Substitution principle
30
E ⌘ F
E + G ⌘ F + G GEH ⌘ GFH
E ⌘ F
E⇤
⌘ F⇤
E ⌘ F
( )

Substitution principle
30
E ⌘ F
E + G ⌘ F + G GEH ⌘ GFH
E ⌘ F
E⇤
⌘ F⇤
E ⌘ F
(T)
( )

Idempotent identities
31
E + E ⌘ E
1⇤
⌘ 1
E⇤
E⇤
⌘ E⇤
E⇤⇤
⌘ E⇤
E + E⇤
⌘ E⇤E⇤
⌘ (1 + E)⇤
1 + 1 ⌘ 1
( )

Star-free expressions are trivial
32
star
E + E ⌘ E(T)
(T)
E + E ⌘ E

Meaning of *
34
E⇤
⌘ 1 + E + EE + EEE + EEEE + EEEEE + · · ·

Meaning of *
34
E⇤
⌘ 1 + EE⇤
E⇤

Meaning of *
34
E⇤
⌘ 1 + EE⇤
E⇤
補題
⾔語　と　について，もし　が空⽂字列を
含まない場合，　は次の式の唯⼀の解(不
動点)となる：
[Arden61]
LK
X = KX [ L.
K⇤
L
K

35
定理
[Salomaa66]
Meaning of *
2つの等式と , 及び
次の推論規則(不動点の解)
E⇤
⌘ 1 + EE⇤
E⇤
⌘ (1 + E)⇤
EF + G ⌘ F " /2 L(E)
F ⌘ E⇤
G
E⇤
⌘ 1 + EE⇤
E⇤
は完全な公理化である．

36
Discussion
Salomaa
star semantical meaning (Arden )
Star syntactical meaning Salomaa
( )

37
Equational axiomatisation
( )

37
Equational axiomatisation
( )
定理
[Redko64][Conway71]
正規表現の等価性の完全な等式公理化は必ず
無限公理化になる(有限公理化は存在しない)．

The most important problem in this area is to
construct a "good" system of rational identities
that would permit us to obtain by a logical
deductive process (i.e. by a rewriting process)
every possible rational identity; such a system
will be called complete.
“
”[Krob91]

Two standard identities of *
39
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F
(sum-star) (E + F)⇤
⌘ E⇤
(FE⇤
)⇤

39
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F
⌘ E⇤
(FE⇤
)⇤
(M)

39
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

39
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
2 (M) (S) star

40
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

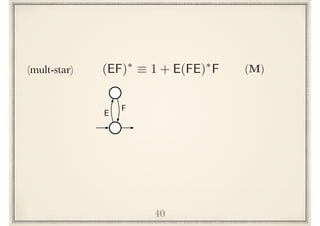
40
E
F
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

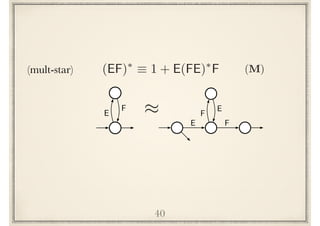
40
E
F
E
F
E
F
⇡
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

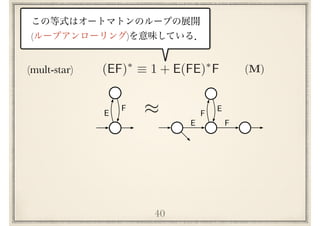
40
E
F
E
F
E
F
⇡
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)
( )

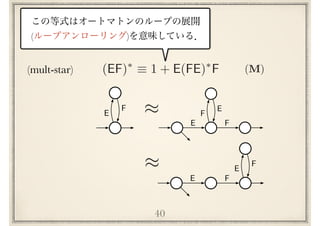
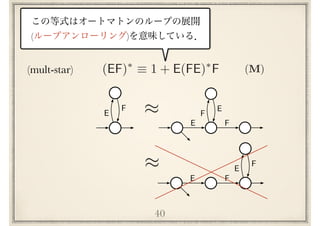
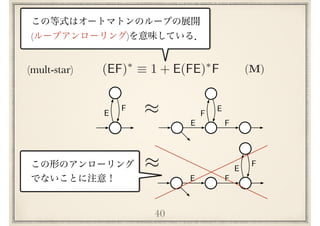
40
E
F
E
F
E
F
⇡
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)
E F
E
F⇡
( )

Exercise 1
41
Prove that is a generalisation of i.e.,E⇤
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
Answer:
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 1
41
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
E⇤
Answer:
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 1
41
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
E⇤
(E · 1)⇤(T)
Answer:
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 1
41
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
E⇤
(E · 1)⇤(T)
1 + E(1 · E)⇤
1
(M)
Answer:
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 1
41
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
E⇤
(E · 1)⇤(T)
1 + E(1 · E)⇤
1
(M)
Answer:
(T)
1 + EE⇤
.
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 1
41
⌘ 1 + EE⇤
,(M)
(M) ` E⇤
⌘ 1 + EE⇤
.
E⇤
(E · 1)⇤(T)
1 + E(1 · E)⇤
1
(M)
Answer:
Corollary: (M) ` 0⇤
⌘ 1.
(T)
1 + EE⇤
.
(mult-star) (EF)⇤
⌘ 1 + E(FE)⇤
F (M)

42
⌘ E⇤
(FE⇤
)⇤
(S)

42
⌘ E⇤
(FE⇤
)⇤
E F
(S)

42
⌘ E⇤
(FE⇤
)⇤
E F
(S)
⇡
E
1 F
1
E

Elegant property of idempotency
43
E + E ⌘ E
1⇤
⌘ 1
E⇤
E⇤
⌘ E⇤
E⇤⇤
⌘ E⇤
E + E⇤
⌘ E⇤E⇤
⌘ (1 + E)⇤
1 + 1 ⌘ 1

Elegant property of idempotency
43
E + E ⌘ E
1⇤
⌘ 1
E⇤
E⇤
⌘ E⇤
E⇤⇤
⌘ E⇤
E + E⇤
⌘ E⇤
(M) (S) (I)
(I)(idempotency)
E⇤
⌘ (1 + E)⇤
1 + 1 ⌘ 1

Exercise 2
44
Prove the following identity
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 2
44
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
1 + 1
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 2
44
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
1 + 1 1 + 1⇤(I)
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 2
44
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
1 + 1 1 + 1⇤(I) (T)
1 + 1 · 1⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 2
44
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
1 + 1 1 + 1⇤(I) (T)
1 + 1 · 1⇤
1⇤ 1.
(M) (I)
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 2
44
(I) ^ (M) ` 1 + 1 ⌘ 1.
Answer:
1 + 1 1 + 1⇤(I) (T)
1 + 1 · 1⇤
1⇤ 1.
(M) (I)
Corollary: (I) ^ (M) ` E + E ⌘ E.
(EF)⇤
⌘ 1 + E(FE)⇤
F (M)

Exercise 3
45
(I) ^ (S) ` E⇤
⌘ (1 + E)⇤
.
Answer:
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)

Exercise 3
45
(I) ^ (S) ` E⇤
⌘ (1 + E)⇤
.
Answer:
(1 + E)⇤
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)

Exercise 3
45
(I) ^ (S) ` E⇤
⌘ (1 + E)⇤
.
Answer:
(1 + E)⇤
1⇤
(E1⇤
)⇤(S)
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)

Exercise 3
45
(I) ^ (S) ` E⇤
⌘ (1 + E)⇤
.
Answer:
(1 + E)⇤ (I)
1(E1)⇤
1⇤
(E1⇤
)⇤(S)
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)

Exercise 3
45
(I) ^ (S) ` E⇤
⌘ (1 + E)⇤
.
Answer:
(1 + E)⇤ (I)
1(E1)⇤
(T)
E⇤
.
1⇤
(E1⇤
)⇤(S)
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(S)
1 + (E + 1)⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(S)
1 + (E + 1)⇤ (I) ^ (S)
1 + E⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(S)
1 + (E + 1)⇤ (I) ^ (S)
1 + E⇤
(M)
1 + 1 + EE⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(S)
1 + (E + 1)⇤ (I) ^ (S)
1 + E⇤
(M)
1 + 1 + EE⇤ (I)
1 + EE⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

46
Answer:
(I) ^ (M) ^ (S) ` E⇤⇤
⌘ E⇤
.
E⇤⇤ (M)
1 + E⇤
E⇤⇤
(S)
1 + (E + 1)⇤ (I) ^ (S)
1 + E⇤
(M)
1 + 1 + EE⇤ (I)
1 + EE⇤
E⇤
.
(M)
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)
Exercise 4
(T)
1 + E⇤
(1E⇤
)⇤

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
E⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
E⇤ (I) ^ (S)
(E + 1)⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
E⇤ (I) ^ (S)
(E + 1)⇤ (S)
E⇤
(1E⇤
)⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
E⇤ (I) ^ (S)
(E + 1)⇤ (S)
E⇤
(1E⇤
)⇤
(T)
E⇤
E⇤⇤
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Exercise 5
47
Answer:
(I) ^ (M) ^ (S) ` E⇤
E⇤
⌘ E⇤
.
E⇤ (I) ^ (S)
(E + 1)⇤ (S)
E⇤
(1E⇤
)⇤
(T)
E⇤
E⇤⇤ (I) ^ (M) ^ (S)
E⇤
E⇤
.
(EF)⇤
⌘ 1 + E(FE)⇤
F
(E + F)⇤
⌘ E⇤
(FE⇤
)⇤
(S)
(M)

Implicational hierarchy
48
E⇤⇤
⌘ E⇤
,
E + E ⌘ E
1⇤
⌘ 1 E⇤
E⇤
⌘ E⇤
1 + 1 ⌘ 1) )
1⇤
1⇤
⌘ 1⇤
,
)
(cf. Fig.12.2 of [Conway71])

Three fundamental identities
49
(E + F)⇤
⌘ (E⇤
F)⇤
E⇤
(S)
(M)(EF)⇤
⌘ 1 + E(FE)⇤
F
(I)1⇤
⌘ 1
(sum-star)
(mult-star)
(idempotency)

49
(E + F)⇤
⌘ (E⇤
F)⇤
E⇤
(S)
(M)(EF)⇤
⌘ 1 + E(FE)⇤
F
(I)1⇤
⌘ 1
(sum-star)
(mult-star)
(idempotency)
Q:(I) ^ (M) ^ (S)

49
(E + F)⇤
⌘ (E⇤
F)⇤
E⇤
(S)
(M)(EF)⇤
⌘ 1 + E(FE)⇤
F
(I)1⇤
⌘ 1
(sum-star)
(mult-star)
(idempotency)
A: !
Q:(I) ^ (M) ^ (S)

Cyclic identities
50
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
( )

Cyclic identities
50
E⇤
⌘ (1 + E)(EE)⇤
(P(2))Example:
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
( )

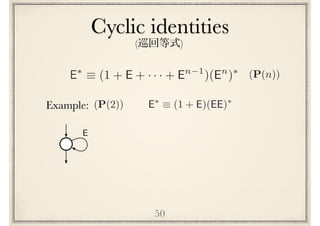
Cyclic identities
50
E⇤
⌘ (1 + E)(EE)⇤
(P(2))Example:
E
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
( )

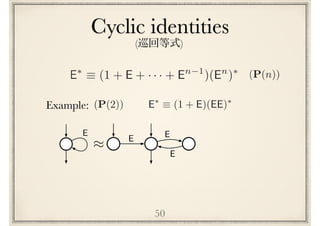
Cyclic identities
50
E⇤
⌘ (1 + E)(EE)⇤
(P(2))Example:
E
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
⇡ E E
E
( )

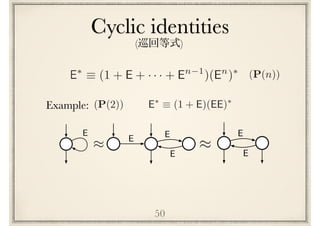
Cyclic identities
50
E⇤
⌘ (1 + E)(EE)⇤
(P(2))Example:
E E
E
⇡
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
⇡ E E
E
( )

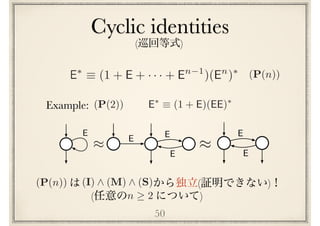
Cyclic identities
50
E⇤
⌘ (1 + E)(EE)⇤
(P(2))Example:
E E
E
⇡
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
⇡ E E
E
( )(P(n)) (I) ^ (M) ^ (S)
n 2( )
( )

(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
51
Q: (I) ^ (M) ^ (S) ^ (P(n))n 2
Cyclic identities

(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
51
A:
Q: (I) ^ (M) ^ (S) ^ (P(n))n 2
Cyclic identities

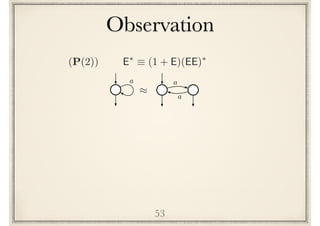
(P(n))E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
51
A:
Q: (I) ^ (M) ^ (S) ^ (P(n))n 2
Cyclic identities
定理
(I) ^ (M) ^ (S) ^ (P(n))n 2
は1⽂字アルファベット　　　上の正規表現
　　において完全．RegA
A = {a}
[Redko64][Conway71]

Observation
53
⇡
E⇤
⌘ (1 + E)(EE)⇤
(P(2))
a a
a

Observation
53
⇡
E⇤
⌘ (1 + E)(EE)⇤
(P(2))
Z/2Z.
a a
a

Observation
53
⇡
E⇤
⌘ (1 + E)(EE)⇤
(P(2))
(P(n)) E⇤
⌘ (1 + E + · · · + En 1
)(En
)⇤
Z/nZ
Z/2Z.
a a
a

Observation
54
1
EF ⇡ FE for any E, F 2 RegA.
Z/nZ
A = {a}

Observation
54
1
EF ⇡ FE for any E, F 2 RegA.
Z/nZ
A = {a}
1
(I) ^ (M) ^ (S) ^ (P(n))n 2
…

Groups as automata
55
G AG
G
G 1 G
G
G

Groups as automata
55
G
L(AG) = G⇤
AG
G
G 1 G
G
G

56
AZ/3ZAZ/2Z
a0 a1
a1
a0
a1
a0
a0
a1a2
a1
a2
a0
a1
a2
a0
a1
a2
a0
Z/2Z = {a0, a1} Z/3Z = {a0, a1, a2}

Group identities
57
C(AG)
(P(G))
G⇤
G

Group identities
57
AZ/2Z
a0 a1
a1
a0
a1
a0
C(AG)
(P(G))
G⇤
G

Group identities
57
AZ/2Z
a0 a1
a1
a0
a1
a0
C(AG)
(P(G))
G⇤
(a0 + a1)⇤
⌘ C(AZ/2Z)
(P(AZ/2Z))
G

Group identities
57
AZ/2Z
a0 a1
a1
a0
a1
a0
C(AG)
(P(G))
G⇤
= (a0 + a1a⇤
0a1)⇤
+ a⇤
0a1(a0 + a1a⇤
0a1)⇤
.
(a0 + a1)⇤
⌘ C(AZ/2Z)
(P(AZ/2Z))
G

Group identities
58
= (a0 + a1a⇤
0a1)⇤
+ a⇤
0a1(a0 + a1a⇤
0a1)⇤
.
(a0 + a1)⇤
⌘ C(AZ/2Z)
(P(AZ/2Z))
C(AG)
(P(G))
G⇤
G

Group identities
58
= (a0 + a1a⇤
0a1)⇤
+ a⇤
0a1(a0 + a1a⇤
0a1)⇤
.
(a0 + a1)⇤
⌘ C(AZ/2Z)
,a0 = 0 a1 = a
⌘ (1 + a)(aa)⇤
(P(AZ/2Z)) (P(2))
a⇤
⌘ (aa)⇤
+ a(aa)⇤
(P(AZ/2Z))
C(AG)
(P(G))
G⇤
G

59
73
Tr(1, 1)= (T1,1+ T1,3T;,3T3,1 +
T r(1, 2) = Tr(1, 1)(TI,~ + T2,3T~,3Taa)(T2,2+ T2,3T~,3T3,2)*
Tr(1, 3) = Tr(1, 1)T1,3T~,3+ Tr(1,2)T2,3T;,3
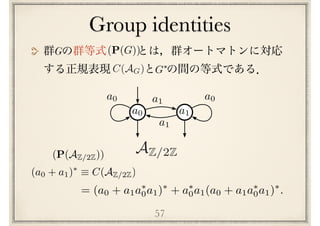
Note that the interpretations of these expressions are quite simple. Indeed, Tr(1, i) is
exactly the set of the words which corresponds to the permutations mapping 1 on i.
COROLLARY V.6 : Let A be an alphabet. Then, the following system :
(M), (S), (P(~,,)),,>__2
is a complete system of B-rational identities for A.
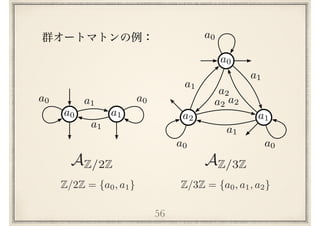
Example : In order to understand the complexity which is hidden under the identities
P(6,~), let us precise the group identity associated with the symmetric group of order 3 :
e#3= {i-- Id, Pl = (123), P2 = (132), al = (23), a2 = (13), a3-- (12)}
Then let us consider the following rational expressions constructed over the alphabet
which is naturally associated with 63 :
Tu=a~+a~l Tm=ap,+a~ 3 T1,3=ap2+a~
T~,, = ap~ + a~ T2,2= ai + ao2 T2,3= ap, + a~,
T3,1 = ap~ + ao~ T3,2= a~ + a~, T3,3= ai + aa~
Observe that the interpretation of the expression T/j is simply the set of the permutations
of 63 that send i on j. With these denotations, we can now give an identity which is
equivalent modulo (M), (S) and P(2) to P(e~a) :
(hi + ca, + ap, + a~,~+ a~ + co2)* .~ Tr(1,1) + Tr(1,2) + Tr(1,3)
where the three expressions Tr(1,1), Tr(1, 2) and Tr(1, 3) stand for :
Example from [Krob91]

59
73
Tr(1, 1)= (T1,1+ T1,3T;,3T3,1 +
T r(1, 2) = Tr(1, 1)(TI,~ + T2,3T~,3Taa)(T2,2+ T2,3T~,3T3,2)*
Tr(1, 3) = Tr(1, 1)T1,3T~,3+ Tr(1,2)T2,3T;,3
Note that the interpretations of these expressions are quite simple. Indeed, Tr(1, i) is
exactly the set of the words which corresponds to the permutations mapping 1 on i.
COROLLARY V.6 : Let A be an alphabet. Then, the following system :
(M), (S), (P(~,,)),,>__2
is a complete system of B-rational identities for A.
Example : In order to understand the complexity which is hidden under the identities
P(6,~), let us precise the group identity associated with the symmetric group of order 3 :
e#3= {i-- Id, Pl = (123), P2 = (132), al = (23), a2 = (13), a3-- (12)}
Then let us consider the following rational expressions constructed over the alphabet
which is naturally associated with 63 :
Tu=a~+a~l Tm=ap,+a~ 3 T1,3=ap2+a~
T~,, = ap~ + a~ T2,2= ai + ao2 T2,3= ap, + a~,
T3,1 = ap~ + ao~ T3,2= a~ + a~, T3,3= ai + aa~
Observe that the interpretation of the expression T/j is simply the set of the permutations
of 63 that send i on j. With these denotations, we can now give an identity which is
equivalent modulo (M), (S) and P(2) to P(e~a) :
(hi + ca, + ap, + a~,~+ a~ + co2)* .~ Tr(1,1) + Tr(1,2) + Tr(1,3)
where the three expressions Tr(1,1), Tr(1, 2) and Tr(1, 3) stand for :
Example from [Krob91]
3 (6 )

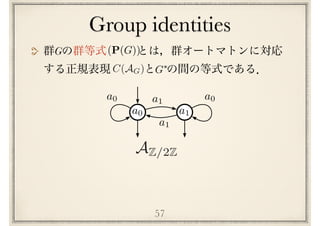
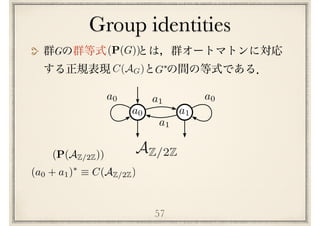
Conway’s conjecture
60
第⼀予想
ここでは全ての有限群の集合，は完全．G
[Conway71]
(I) ^ (M) ^ (S) ^ (P(G))G2G

Conway’s conjecture
60
第⼀予想
ここでは全ての有限群の集合，は完全．G
[Conway71]
(I) ^ (M) ^ (S) ^ (P(G))G2G
ここで　は次の対称群，は完全．Sn n
(I) ^ (M) ^ (S) ^ (P(Sn))n 2
第⼆予想

Krob’s answer
61
Conway 20 1991
Daniel Krob [Krob91]

Krob’s answer
61
Conway 20 1991
Krob [Krob91] 140

Krob’s answer
61
Conway 20 1991
Krob [Krob91] 140
[Krob91]

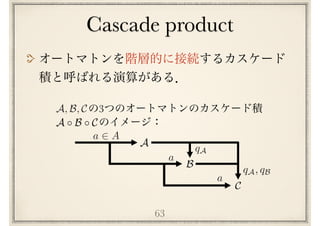
Cascade product
63
A
B
C
a 2 A
a
a
qA
qA, qB
A B C
3A, B, C

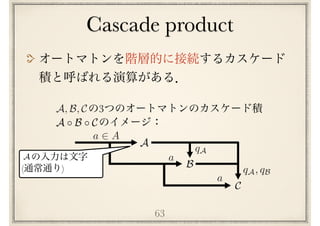
Cascade product
63
A
B
C
a 2 A
a
a
qA
qA, qB
A B C
3A, B, C
( )
A

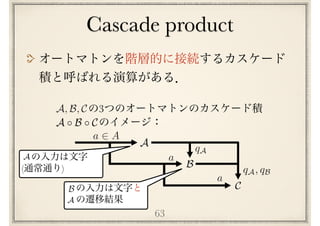
Cascade product
63
A
B
C
a 2 A
a
a
qA
qA, qB
A B C
3A, B, C
( )
A
B
A

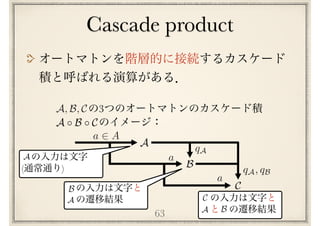
Cascade product
63
A
B
C
a 2 A
a
a
qA
qA, qB
A B C
3A, B, C
( )
A
B
A
BA
C

64
定理
[KR65]
任意のオートマトン　はリセットオートマトン
と群オートマトンのカスケード積の形に分解できる．
つまりオートマトンの列　　　　　　，ここで各　
はリセットオートマトンか群オートマトン，が存在
して次が成り立つ：
A
B1, B2, · · · , Bn
A  B1 B2 · · · Bn
Bi
Krohn-Rhodes theorem

The reset automaton f
65
0 1
ba
a
b ✓
a b
a b
◆
R
R
( )

65
0 1
ba
a
b ✓
a b
a b
◆
R
R
✓
a b
a b
◆⇤
=
✓
(a + bb⇤
a)⇤
a⇤
b(b + aa⇤
b)⇤
b⇤
a(a + bb⇤
a)⇤
(b + aa⇤
b)⇤
◆
( )

65
0 1
ba
a
b ✓
a b
a b
◆
R
R
C(R) = 1 0
✓
a b
a b
◆⇤ ✓
1
1
◆
= (a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤
✓
a b
a b
◆⇤
=
✓
(a + bb⇤
a)⇤
a⇤
b(b + aa⇤
b)⇤
b⇤
a(a + bb⇤
a)⇤
(b + aa⇤
b)⇤
◆
( )

Identity of
66
0 1
ba
a
b
R
R
(a + b)⇤
⌘ (a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤

Exercise 6
67
(M) ^ (S) ` (a + b)⇤
⌘ (a + bb⇤
a)⇤
+ a⇤
b(b + aa⇤
b)⇤
.

68
Answer: (M)
(T)
(S)
(M)
(M)
(a + b)⇤
⌘ 1 + (a + b)⇤
(a + b)
⌘ 1 + (a + b)⇤
a + (a + b)⇤
b
⌘ 1 + b⇤
(ab⇤
)⇤
a + a⇤
(ba⇤
)⇤
b
⌘ b⇤
(ab⇤
)⇤
a + (a⇤
b)⇤
⌘ b⇤
(ab⇤
)⇤
a + 1 + a⇤
b(a⇤
b)⇤
⌘ (b⇤
a)⇤
+ a⇤
b⇤
(a⇤
b)⇤
⌘ ((1 + bb⇤
)a)⇤
+ a⇤
b((1 + aa⇤
)b)⇤
⌘ (a + bb⇤
a)⇤
a⇤
b(b + aa⇤
b)⇤
.
(M)
(T)
(T)
Exercise 6

69
定理
[KR65]
任意のオートマトン　はリセットオートマトン
と群オートマトンのカスケード積の形に分解できる．
つまりオートマトンの列　　　　　　，ここで各　
はリセットオートマトンか群オートマトン，が存在
して次が成り立つ：
A
B1, B2, · · · , Bn
A  B1 B2 · · · Bn
Bi
Krohn-Rhodes theorem

Conway
Conway Last Conjecture’s
V

71
AZ/3ZAZ/2Z
a0 a1
a1
a0
a1
a0
a0
a1a2
a1
a2
a0
a1
a2
a0
a1
a2
a0
1 a1
( (monogenic group) )

72
a0 a1
a1
a1
a0
a1a2
a1
a1
a1
A0
Z/2Z A0
Z/3Z

73
事実
任意の対称群　は2つの元　　　　　　と
　　　　によって⽣成される．
Sn a = (1 2 · · · n)
b = (1 2)

73
事実
任意の対称群　は2つの元　　　　　　と
　　　　によって⽣成される．
Sn a = (1 2 · · · n)
b = (1 2)
3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5

(R(n))
Symmetric identities
(E + F)⇤
⌘
⇣
(E + F)(F + (EF⇤
)n 2
E)
⌘⇤⇣
1 + (E + F)
n 2X
k=0
(EF⇤
)k
⌘
( )

(R(n))
(E + F)⇤
⌘
⇣
(E + F)(F + (EF⇤
)n 2
E)
⌘⇤⇣
1 + (E + F)
n 2X
k=0
(EF⇤
)k
⌘
( )
n
2 C(A0
Sn
)

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
( )

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )
1

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )
1 2

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )
1 2 3

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )
1 2 3 4

3
2
1
5
4
a + b
a
b
a
b
a
b
a
b
A0
S5
(R(5))
(a + b)⇤
⇣
(a + b)(b + (ab⇤
)3
a)
⌘⇤⇣
1 + (a + b)(1 + ab⇤
+ (ab⇤
)2
+ (ab⇤
)3
)
⌘
⌘
1
( )
1 2 3 4 5

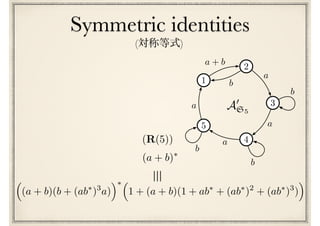
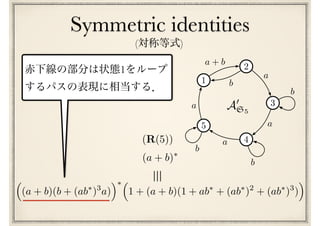
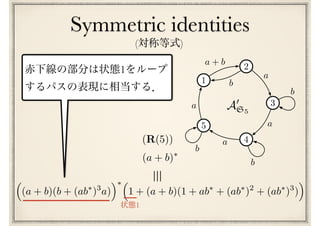
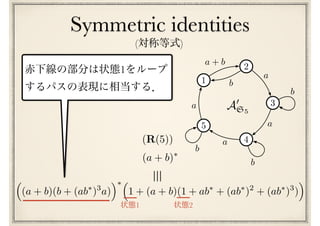
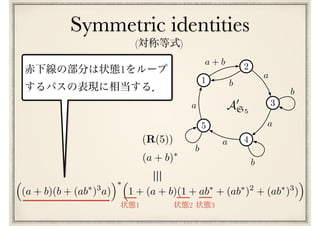
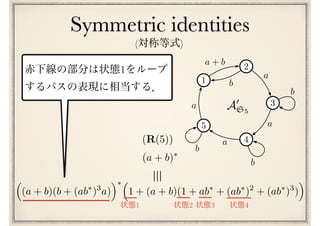
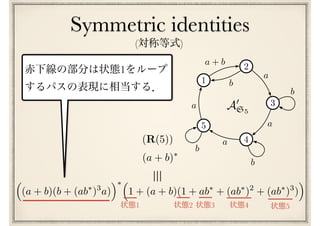
最終予想
(I) ^ (M) ^ (S) ^ (R(n))n 2
Conway’s last conjecture
[Conway71]

Bibliography
79
[Kleene51] Kleene S., “Representation of Events in Nerve Nets and Finite
Automata”, 1951.
[Arden61] Arden D. N., “Delayed logic and finite state machines”, 1961.
[Redko64] Redko V. N., “On defining relations for the algebra of regular
events” ( ), 1964.
[KR65] Krohn K. and Rhodes J., “Algebraic Theory of Machines. I. Prime
Decomposition Theorem for Finite Semigroups and Machines”, 1965.
[Salomaa66] Salomaa A., “Two complete axiom systems for the algebra of regular
events”, 1966.
[Conway71] Conway J. H., “Regular algebras and finite machines”, 1971.
[Krob91] Krob D., “Complete systems of B-rational identities”, 1991.

正規表現に潜む対称性　〜等式公理による等価性判定〜

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to 正規表現に潜む対称性　〜等式公理による等価性判定〜

Similar to 正規表現に潜む対称性　〜等式公理による等価性判定〜 (20)

More from Ryoma Sin'ya

More from Ryoma Sin'ya (12)

Recently uploaded

Recently uploaded (20)