More Related Content
PDF
PDF
PPT
Algorithm - Fibonacci Phyllotaxis by Asymmetric Cell Division PDF
PDF
PDF
ZIP
PPTX
Similar to ワイソフ配列について
PDF
【Unity道場】ゲーム制作に使う数学を学習しよう PDF
PPTX
PDF
「現実世界に活かす数学」 (麻布高等学校、教養総合、数学講義 5 回目) PDF
PPTX
PDF
PDF
PPTX
PPT
PDF
PDF
PDF
PDF
PDF
PDF
PDF
JOI春季ステップアップセミナー 2021 講義スライド PDF
競技プログラミング練習会2015 Normal 第1回 PDF
R language definition3.1_3.2 PDF
More from Yu(u)ki IWABUCHI
PDF
サイエンスアゴラ研究100連発 〜目に見えて楽しい数学〜 PPTX
PDF
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
音楽にまつわる数学 〜「倍音」で理解する和音と音色〜 PPTX
PPTX
PPTX
Bad Apple Curve!! 〜フーリエ記述子でアニメーション作ってみた〜 PPTX
PPTX
ワイソフ配列について
- 1.
- 2.
- 3.
- 4.
- 5.
最も簡単なインタースパージョン
名前がないので「物智配列」と命名
0 12 3 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
ぶつち
- 6.
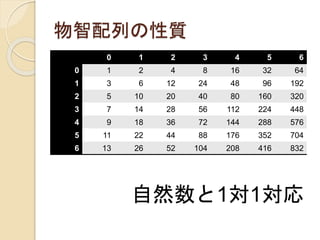
物智配列の性質
自然数と1対1対応
0 1 23 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
- 7.
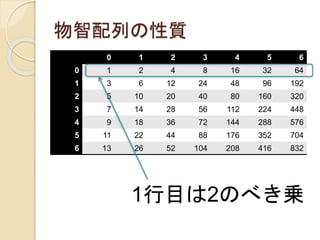
物智配列の性質
1行目は2のべき乗
0 1 23 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
- 8.
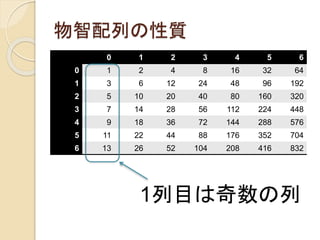
物智配列の性質
0 1 23 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
1列目は奇数の列
- 9.
物智配列の性質
縦は等差数列
(線形的)
0 1 23 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
- 10.
物智配列の性質
横は公比2の等比数列
(指数関数的)
0 1 23 4 5 6
0 1 2 4 8 16 32 64
1 3 6 12 24 48 96 192
2 5 10 20 40 80 160 320
3 7 14 28 56 112 224 448
4 9 18 36 72 144 288 576
5 11 22 44 88 176 352 704
6 13 26 52 104 208 416 832
- 11.
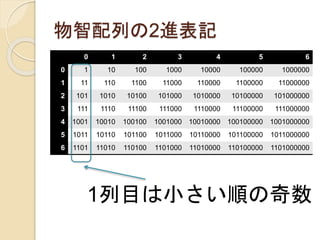
物智配列の2進表記
1列目は小さい順の奇数
0 1 23 4 5 6
0 1 10 100 1000 10000 100000 1000000
1 11 110 1100 11000 110000 1100000 11000000
2 101 1010 10100 101000 1010000 10100000 101000000
3 111 1110 11100 111000 1110000 11100000 111000000
4 1001 10010 100100 1001000 10010000 100100000 1001000000
5 1011 10110 101100 1011000 10110000 101100000 1011000000
6 1101 11010 110100 1101000 11010000 110100000 1101000000
- 12.
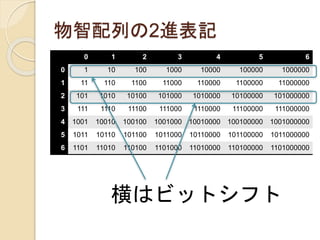
0 1 23 4 5 6
0 1 10 100 1000 10000 100000 1000000
1 11 110 1100 11000 110000 1100000 11000000
2 101 1010 10100 101000 1010000 10100000 101000000
3 111 1110 11100 111000 1110000 11100000 111000000
4 1001 10010 100100 1001000 10010000 100100000 1001000000
5 1011 10110 101100 1011000 10110000 101100000 1011000000
6 1101 11010 110100 1101000 11010000 110100000 1101000000
物智配列の2進表記
横はビットシフト
- 13.
- 14.
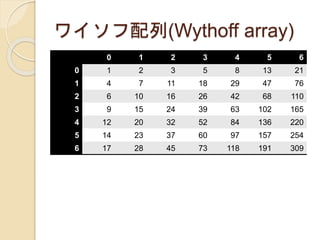
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
- 15.
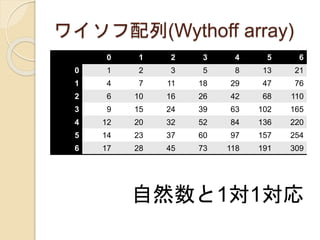
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
自然数と1対1対応
- 16.
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
1行目はフィボナッチ数
- 17.
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
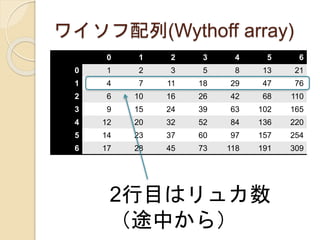
2行目はリュカ数
(途中から)
- 18.
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
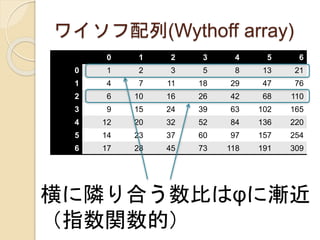
横に隣り合う数比はφに漸近
(指数関数的)
- 19.
ワイソフ配列(Wythoff array)
0 12 3 4 5 6
0 1 2 3 5 8 13 21
1 4 7 11 18 29 47 76
2 6 10 16 26 42 68 110
3 9 15 24 39 63 102 165
4 12 20 32 52 84 136 220
5 14 23 37 60 97 157 254
6 17 28 45 73 118 191 309
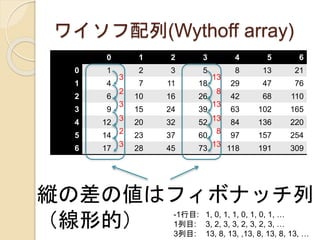
縦の差の値はフィボナッチ列
(線形的) -1行目: 1, 0, 1, 1, 0, 1, 0, 1, …
1列目: 3, 2, 3, 3, 2, 3, 2, 3, …
3列目: 13, 8, 13, ,13, 8, 13, 8, 13, …
3
2
3
3
2
3
13
8
13
13
8
13
- 20.
フィボナッチ記数法
(Fibonacci notation)
桁の重みがFn
1が連続しない
8 5 3 2 1
0 0 0 0 0 0
0 0 0 0 1 1
0 0 0 1 0 2
0 0 1 0 0 3
0 0 1 0 1 4
0 1 0 0 0 5
0 1 0 0 1 6
8 5 3 2 1
0 1 0 1 0 7
1 0 0 0 0 8
1 0 0 0 1 9
1 0 0 1 0 10
1 0 1 0 0 11
1 0 1 0 1 12
- 21.
ワイソフ配列の
フィボナッチ記数表記
0 1 23 4
0 1 10 100 1000 10000
1 101 1010 10100 101000 1010000
2 1001 10010 100100 1001000 10010000
3 10001 100010 1000100 10001000 10001000
0
4 10101 101010 1010100 10101000 10101000
0
フィボナッチ記数法において
物智配列と同様の性質
- 22.
応用
隣り合う数比Wm, n/Wm+1,nがφに漸近
→隣接2数の比からφの近似値を算出可能
Wm, nが2のべき乗なら、
Wm+1, nのビットシフトが近似値となる
110011110001101111
100000000000000000
110011110001101111
÷ )
.
→ 212079
→ 131072
→ 1.61803
- 23.
- 24.
- 25.
- 26.
- 28.
- 29.