Download as PDF, PPTX
![[Dl輪読会]introduction of reinforcement learning](https://cdn.slidesharecdn.com/ss_thumbnails/dlintroductionofreinforcementlearning-161121061444-thumbnail.jpg?width=640&height=640&fit=bounds)
Ml professional bandit_chapter1
- 1.
- 2. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成 • はなしません
- 3. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成
- 4.
- 5. 儲けるための戦略 • 儲けるためには • 当たる確率が最も高いスロットマシーンを選択 •どうやって選択するか？ • 例：各スロットn回ずつ引き， 残りの(100-n)回で最も当たったスロットを回す イラスト： http://www.irasutoya.com/
- 6. 儲けるための戦略 • 儲けるためには • 当たる確率が最も高いスロットを選択 •どうやって良いスロット選択するか？ • 例：各スロットn回ずつ引き， 残りの(100-n)回で最も当たったスロットを選択 イラスト： http://www.irasutoya.com/
- 7. 探索と知識利用のトレードオフ • n を小さくすると・・・ •当たったスロットを多く引けるものの， 真に当たりやすいスロットであるかの見極めが難しい • nを大きくすると・・・ • 当たりやすいスロットの見極めができるかもしれないが， 当たりやすいスロットを多くは引けない • 良いアームを探索する必要がある一方で 探索で得たアームを引く知識利用を行う必要もある • 探索と知識利用はトレードオフとなる
- 8. バンディット問題とは • 選択肢の集合から報酬が良い選択を行い， 報酬の最大化を目指す逐次決定問題 • e.g)良いスロットを選択し，儲けを最大化する •探索により得られた知識をもとに次の選択肢を 決定する戦略を方策（policy）と呼ぶ
- 9. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成
- 10.
- 11. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成
- 12. 確率的バンディットと敵対的バンディット • バンディット問題は大きく2つに分けて • 確率バンディット（stochasticbandit） • アームの報酬を確率分布により生成 • （詳細は第4章で） • 敵対的バンディット（adversarial bandit） • プレイヤーのアーム選択方法を知った上で 敵対者が報酬を最小化する • ただし敵対者はプレイヤーがアームを選択する前に 報酬を設定する • （詳細は第5章で）
- 13. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成
- 14. プレイヤー方策の評価法 • バンディット問題において 以下の2つのいずれかの最大化を目指す • 有限時間区間（finitehorizon） における累積報酬（cumulative raword） • 無限時間区間（infinite horizon） における幾何割引（geometric discount）された累積報酬
- 15. プレイヤー方策の評価法 • バンディット問題において 以下の2つのいずれかの最大化を目指す • 有限時間区間（finitehorizon） における累積報酬（cumulative raword） • 無限時間区間（infinite horizon） における幾何割引（geometric discount）された累積報酬 近年では主流
- 16. プレイヤー方策の評価法 • バンディット問題において 以下の2つのいずれかの最大化を目指す • 有限時間区間（finitehorizon） における累積報酬（cumulative raword） • 無限時間区間（infinite horizon） における幾何割引（geometric discount）された累積報酬 近年では主流 𝑡=1 𝑇 𝑋𝑖 𝑡 (𝑡)
- 17. プレイヤー方策の評価法 • バンディット問題において 以下の2つのいずれかの最大化を目指す • 有限時間区間（finitehorizon） における累積報酬（cumulative raword） • 無限時間区間（infinite horizon） における幾何割引（geometric discount）された累積報酬 近年では主流 𝑡=1 𝑇 𝑋𝑖 𝑡 (𝑡) 時刻tに選択するアーム
- 18. プレイヤー方策の評価法 • バンディット問題において 以下の2つのいずれかの最大化を目指す • 有限時間区間（finitehorizon） における累積報酬（cumulative raword） • 無限時間区間（infinite horizon） における幾何割引（geometric discount）された累積報酬 近年では主流 𝑡=1 𝑇 𝑋𝑖 𝑡 (𝑡) 時刻tにおける報酬
- 19. Regretによる方策の評価 • 累積による評価の場合， 報酬の組み合わせにも依存してしまう • ある累積報酬を目標値とし，それとの差を比較する ➝リグレット（regret） RegretT = max 𝑖∈{1,…𝐾} 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡)
- 20. Regretによる方策の評価 • 累積による評価の場合， 報酬の組み合わせにも依存してしまう • ある累積報酬を目標値とし，それとの差を比較する ➝リグレット（regret） RegretT = max 𝑖∈{1,…𝐾} 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡) 同じ選択を続けたとき, 累積報酬が最大となる選択
- 21. Regretによる方策の評価 • 累積による評価の場合， 報酬の組み合わせにも依存してしまう • ある累積報酬を目標値とし，それとの差を比較する ➝リグレット（regret） RegretT = max 𝑖∈{1,…𝐾} 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡) 方策により決定した 選択の累積報酬
- 22. Regretによる方策の評価 • 方策の選択i(t)や報酬Xi(t)は確率的であることが多い ➝複数試行のリグレットの平均値である 期待リグレット（expected regret）をよく用いる 𝐄Regret T = 𝐄 max 𝑖∈{1,…𝐾} 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡)
- 23. Regretによる方策の評価 • 方策の選択i(t)や報酬Xi(t)は確率的であることが多い ➝複数試行のリグレットの平均値である 期待リグレット（expected regret）をよく用いる ➝さらに擬リグレット（pseudoregret）も用いられる 𝐄 Regret T = 𝐄 max 𝑖∈{1,…𝐾} 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡) Regret(T) = max 𝑖∈{1,…𝐾} 𝐄 𝑡=1 𝑇 𝑋𝑖(𝑡) − 𝑡=1 𝑇 𝑋𝑖(𝑡)(𝑡)
- 24. 構成 • 1.1 はじめに •1.2 バンディット問題の例 • 1.3 確率的バンディットと敵対的バンディット • 1.4 プレイヤー方策の評価法 • 1.5 バンディット問題の歴史 • 1.6 関連分野 • 1.7 本書の構成 • はなしません
- 25. バンディット問題の歴史 • バンディット問題のような問題は古くから研究されていた • 適応的割り当て（adaptiveallocation） • 逐次的割り当て（sequential allocation） • 1950年代~ • 確率的バンディットの研究スタート • 平均擬リグレット • １腕バンディット問題 • 1990年代~ • 強化学習による行動価値観数の学習 • 敵対的バンディットに関する研究スタート • 2000年代~ • UCB方策の提案 • モンテカルロ木探索の導入
- 26. バンディット問題の歴史 • バンディット問題のような問題は古くから研究されていた • 適応的割り当て（adaptiveallocation） • 逐次的割り当て（sequential allocation） • 1950年代~ • 確率的バンディットの研究スタート • 平均擬リグレット • １腕バンディット問題 • 1990年代~ • 強化学習による行動価値観数の学習 • 敵対的バンディットに関する研究スタート • 2000年代~ • UCB方策の提案 • モンテカルロ木探索の導入
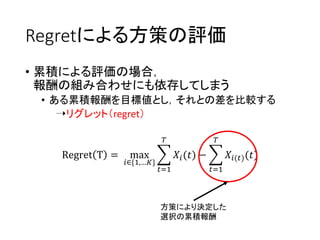
- 27. バンディット問題の歴史 - UCB方策 - •ライらは期待報酬の信頼上限（upper confidence bound）を アーム選択指標とする方策を提案（1985年） • 指標が複雑で計算が困難 • ブルネタスらが計算が容易であるような指標に 改良した方策を提案（1996年） ➝やはり指標は複雑
- 28. バンディット問題の歴史 - UCB方策 - •ライらは期待報酬の信頼上限（upper confidence bound）を アーム選択指標とする方策を提案（1985年） • 指標が複雑で計算が困難 • ブルネタスらが計算が容易であるような指標に 改良した方策を提案（1996年） ➝やはり指標は複雑 アウアーらがUCB方策（3章）を提案 ➝ 漸近的な性能は劣るものの，指標が直感的 様々な分野に応用され機械学習分野においても盛んに
- 29. バンディット問題の歴史 - 様々な応用 - •コックシスらはUCTアルゴリズム（Upper Confidence bound applied to Tree algorithm）（第10章）の提案 • モンテカルロ木探索にUCB方策を導入 • 葉節点の選択にUCB方策を利用する • Lin UCB方策（LinUCB policy）（第7章）の提案 • UCB方策を線形モデル上のバンディット問題に拡張 • 推薦システムへの応用 • コールドスタート問題を解消する手法として有効
- 30. バンディット問題の歴史 - 敵対的バンディット - •1995年にアウアーらがExp3方策（Exponential-weight policy for Exploration and Exploitation policy）（第5章）を提案 • Hedgeアルゴリズム（第5章）をバンディット問題に適応 • 過去の損失に応じて選択確率を決定する • 性能改善の余地があった • 2009年にオーディベールらによりINF方策（Implicitly Normalized Forcaster policy）（第5章）の提案 • Exp3方策で改善の余地があった部分を解消