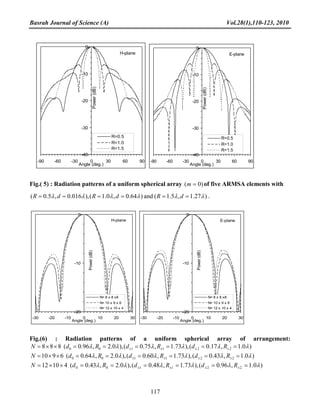
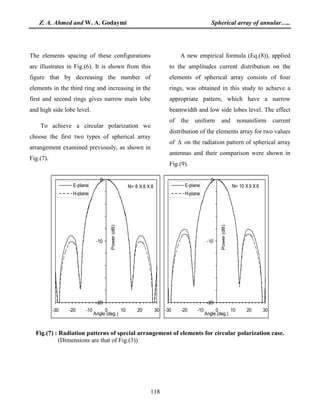
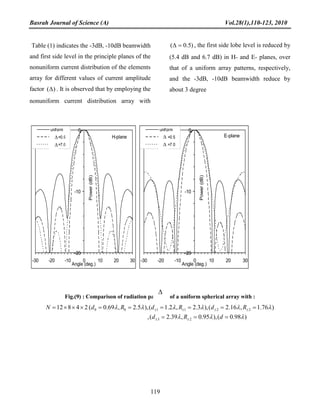
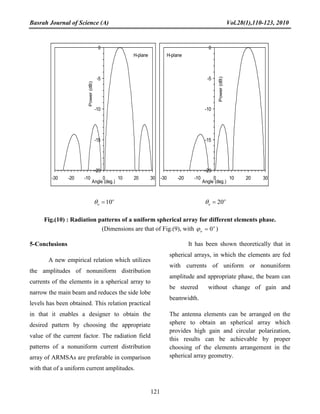
The paper presents an analytical study of spherical arrays of annular ring microstrip antennas (ARMSA) excited by electric dipole, focusing on their nonuniform current amplitude distributions. It highlights the benefits of such arrays in achieving narrow beamwidth and low side lobe levels, as well as their application in circular polarization and omni-directional coverage. The study provides empirical formulas for optimizing these antennas' performance while analyzing their radiation properties through various configurations.