This thesis by Eng. Ahmad Farrag El-Sayed focuses on the attitude control of remote sensing satellites using a magnetic actuator due to its advantages of low power consumption, small mass, and reliability. A comparison of conventional controllers is conducted, leading to the development of a new combined control algorithm that demonstrates improved performance through simulations. The research emphasizes the importance of effective attitude acquisition and stabilization methods for satellite operation.

1. A Combined Attitude Magnetic Controller for
Remote Sensing Satellite
by
Eng. AHMAD FARRAG EL-SAYED
A Thesis Submitted to the
Faculty of Engineering at Cairo University
in Partial Fulfillment of the
Requirements for the Degree of
Master of Science
in
Electrical Power and Machines
FACULTY OF ENGINEERING
CAIRO UNIVERSITY
GIZA, EGYPT
Jun 2010

2. II
A Combined Attitude Magnetic Controller for
Remote Sensing Satellite
by
Eng. AHMAD FARRAG EL-SAYED
A Thesis Submitted to the
Faculty of Engineering at Cairo University
in Partial Fulfillment of the
Requirements for the Degree of
Master of Science
in
Electrical Power and Machines
Under the supervision of
Dr. Hassan Mohamed Rashad
Electrical Power and Machines Dept.
Faculty of Engineering – Cairo University
FACULTY OF ENGINEERING
CAIRO UNIVERSITY
GIZA, EGYPT
Jun 2010
Prof. Dr. Ahmed Bahgat Gamal Bahgat Dr. Ahmed Yehya El-Raffie
Electrical Power and Machines Dept. National Authority for Remote sensing and
Space Since.

3. III
A Combined Attitude Magnetic Controller for
Remote Sensing Satellite
by
Eng. AHMAD FARRAG EL-SAYED
A Thesis Submitted to the
Faculty of Engineering at Cairo University
in Partial Fulfillment of the
Requirements for the Degree of
Master of Science
in
Electrical Power and Machines
Approved by the
Examining committee:
Prof. Dr. Ahmed Bahgat Gamal Bahgat, Thesis Main Advisor
Prof. Dr. Abed EL-Monem Abed EL-Zaher Wahdan
Faculty of Engineering Ain Shams University
Prof. Dr. Mohamed Mohamed Faheem Saker
Faculty of Engineering Cairo University
Prof. Dr. Ahmed Yehia EL-Raffie
National Authority for Remote Sensing and Space Since
Prof. Dr.Hassan Mohamed Rashad
Faculty of Engineering Cairo University
FACULTY OF ENGINEERING
CAIRO UNIVERSI TY
GIZA, EGYPT
Jun 2010

4. IV
Abstract
The problem of attitude control of remote sensing satellite using
magnetic actuators is considered in this thesis. Magnetic actuator was used
because of it is a low power consumption, small mass, low cost and reliable
attitude actuator. The attitude control problem of the satellite involves angular
velocity suppression, attitude acquisition and finally attitude stabilization will
be solved by magnetic actuator only. A comparison between the commonly
used controllers for satellite attitude control is presented. The comparison
parameters are the total consumed power, the time required to accomplish the
angular velocity suppression and attitude acquisition, calculation time of the
control algorithm and steady state error in angles and angular velocity. The
simulation is done using the complete non linear model of satellite. Based on
results, a new combined control algorithm was developed to assemble the
advantages of these commonly used controllers. Simulation results showed the
validity of the developed combined algorithm.

5. V
Acknowledgements
I would like to take the opportunity to express my thanks to the people who
have made my studies an exciting experience of professional and cultural
discovery.
Firstly I would like to thank my senior supervisor Professor Ahmad Bahgat
for his guidance and support in this thesis.
I extend my special thanks to my second supervisor Dr.Ahmad EL-Raffie . for
his kind effort and assistance during this work
Also my deep thank to my supervisor Professor Hassan Rashad for his
support and assistance in this thesis
My appreciation also belongs to Egyptian Space Program (ESP) at which I
am working for assistance provided by my mangers and colleagues. Besides the
technical training during EgyptSat1 project and financial support for this thesis.
I am so grateful to my Automatic control Teacher Dr Mahmoud Kamel for his
support during my undergraduate study
To my thanks also, to Dr Yefemainco ,Mr Badmasteriv and Mr Koshtica
form Khartron Konsat. Zporozhye, Ukraine, for their technical assistance to me
in understanding the attitude control problem during Egptsat1 project.
I want to express my gratitude to My Parents, who always believed that I
would succeed in master. I would like to express my deepest thanks to them for
their patience and support during all those years.
I am deeply indebted to My Wife for her continues support and taking care of
our kids during all those hard years. She always believed that I can go on easily
in this study, I appreciate her support.

6. VI
Contents
Abstract IV
Acknowledgment V
Table of contents VI
List of figures XI
List of Tables XV
Acronyms XVI
List of symbols XVII
CHAPTER (1) Introduction 1
CHAPTER (2) SPACE SEGMENT OVERVIEW 5
2.1 Space System Composition.................................................................. 5
2.2 Satellite Architecture............................................................................ 6
2.2.1 Satellite Payload ........................................................................... 6
2.2.1.1 Communication......................................................................... 6
2.2.1.2 Positioning and Navigation....................................................... 6
2.2.1.3 Weather ..................................................................................... 7
2.2.1.4 Remote Sensing......................................................................... 8
2.2.2 Satellite Bus .................................................................................. 9
2.2.2.1 The Structural Subsystem ....................................................... 10
2.2.2.2 Attitude Determination and Control Subsystem..................... 10
2.2.2.3 Propulsion Subsystem............................................................. 10
2.2.2.4 Communications Subsystem................................................... 11
2.2.2.5 Command and Data Handling Subsystem .............................. 11
2.2.2.6 Power System.......................................................................... 11
2.2.2.7 The Thermal Subsystem.......................................................... 12
2.3 Satellite Orbits.................................................................................... 12
2.3.1 Special Orbits.............................................................................. 16
2.3.1.1 Low Earth Orbit (LEO)........................................................... 16
2.3.1.2 Medium Earth Orbit (MEO) ................................................... 16
2.3.1.3 Geostationary/Geosynchronous Earth Orbit (GEO) ............... 17

7. VII
2.3.1.4 Polar Earth Orbit ..................................................................... 17
2.3.1.5 Sun Synchronous Orbits (SSO)............................................... 18
2.3.1.6 Molniya Orbit.......................................................................... 18
CHAPTER (3) Attitude Determination and Control Subsystem ADCS 20
3.1 Internal influence between satellite mission and other subsystems
upon ADCS ................................................................................................... 20
3.1.1 Internal influence between ADCS and Mission requirement..... 20
3.1.2 Internal influence between ADCS and Structure Subsystem ..... 21
3.1.3 Internal influence between ADCS and Power Subsystem.......... 21
3.1.4 Internal influence between ADCS and Communication
Subsystem.................................................................................................. 21
3.1.5 Internal influence between ADCS and Command and Data
Handling Subsystem.................................................................................. 22
3.1.6 Internal influence between ADCS and thermal subsystem ........ 22
3.2 ADCS Tasks....................................................................................... 22
3.3 Satellite operational modes ................................................................ 23
3.3.1 De-tumbling mode (DM)............................................................ 23
3.3.2 Standby Mode (SM).................................................................... 23
3.3.3 High Accuracy Mode (HAM) or Imaging Mode (IM)............... 23
3.3.4 Emergency Mode (EM) .............................................................. 24
3.3.5 Transferring from one operational mode to another................... 24
3.4 ADCS devices .................................................................................... 25
3.4.1 ADCS Sensors ............................................................................ 25
3.4.1.1 Earth’s Horizon sensor............................................................ 26
3.4.1.2 Sun sensor ............................................................................... 26
3.4.1.3 Star mapper ............................................................................. 27
3.4.1.4 Magnetometers........................................................................ 28
3.4.1.5 Inertial Sensor or Gyro............................................................ 29
3.4.2 ADCS Actuators ......................................................................... 32
3.4.2.1 Momentum and Reaction Wheel............................................. 32

8. VIII
3.4.2.2 Magnetic actuators .................................................................. 33
3.4.2.3 Thruster ................................................................................... 35
3.5 Disturbance Environment................................................................... 36
3.5.1 Gravity Gradient Disturbance..................................................... 36
3.5.2 Magnetic Field Disturbance........................................................ 37
3.5.3 Solar Radiation Pressure Disturbance ........................................ 38
3.5.4 Aerodynamic Disturbance .......................................................... 39
3.6 Attitude Control techniques ............................................................... 39
3.6.1 Passive Control ........................................................................... 40
3.6.1.1 Passive magnetic..................................................................... 40
3.6.1.2 Gravity-gradient stability ........................................................ 41
3.6.1.3 Spin stabilization..................................................................... 42
3.6.1.3.1. Single Spin........................................................................... 42
3.6.1.3.2. Dual Spin............................................................................. 43
3.6.2 Active control techniques ........................................................... 43
3.6.2.1 Momentum exchange Wheels................................................. 44
3.6.2.2 Magnetic actuators .................................................................. 44
3.6.2.3 Thrusters.................................................................................. 44
CHAPTER (4) Control System Modelling 45
4.1 Reference Coordinate Systems .......................................................... 45
4.1.1 Geocentric Inertial Coordinate System....................................... 45
4.1.2 Greenwich Coordinate System ................................................... 45
4.1.3 Orbital Coordinate System.......................................................... 47
4.1.4 Body Coordinate System ............................................................ 47
4.1.5 Device Coordinate System.......................................................... 48
4.2 Modeling of Satellite Rotation Around it's Center of Mass............... 49
4.2.1 Model of Dynamic Equation....................................................... 50
4.2.2 Model of Kinematic Equation..................................................... 57
4.2.3 Linearized Equations of Motion ................................................. 59
4.2.4 Gravity Gradient Stability........................................................... 64

9. IX
4.3 Satellite center of mass motion model ............................................... 66
4.3.1 Satellite orbits and Keplerian elements ...................................... 66
CHAPTER (5) Analysis of Conventional Controllers and Development of a
new Combined Controller 70
5.1 Attitude Magnetic control concept..................................................... 70
5.2 Controllability .................................................................................... 73
5.3 Angular Velocity Suppression ........................................................... 74
5.3.1 Angular suppression using velocity feed back ........................... 75
5.3.1.1 Energy Considerations ............................................................ 75
5.3.1.2 Lyapunov Stability.................................................................. 77
5.3.2 Angular suppression using B-dot technique............................... 80
5.3.2.1 Angular suppression using B-dot technique No.1 .................. 81
5.3.2.2 Angular suppression using B-dot technique No2 ................... 82
5.3.2.3 Angular suppression using B-dot technique No3 ................... 83
5.3.3 Simulation verification ............................................................... 85
5.3.3.1 Simulations results for angular velocity feedback.................. 87
5.3.3.2 Simulation results for B-dot techniques.................................. 88
5.3.4 Comparison between angular velocity suppression algorithms . 92
5.4 Attitude acquisition and stabilization algorithms............................... 93
5.4.1 PD-Like Controller ..................................................................... 94
5.4.1.1 Checking the stability of PD-Like Controller......................... 95
5.4.2 Sliding Mode Controller............................................................. 96
5.4.2.1 Sliding Manifold Design......................................................... 97
5.4.2.2 Sliding Condition Development.............................................. 98
5.4.3 Linear Quadratic Regulator ...................................................... 100
5.4.4 Simulation verification ............................................................. 102
5.4.4.1 Simulations results for PD-like controller ............................ 104
5.4.4.2 Simulations results for sliding mode controller.................... 106
5.4.4.3 Simulations results for LQR ................................................. 109

10. X
5.4.5 Comparison between attitude acquisition and stabilization
algorithms ................................................................................................ 112
5.5 Combined attitude control................................................................ 114
5.5.1.1 Simulations results for Combined algorithm ........................ 116
CHAPTER (6) Conclusion and Future Work 119
Appendix A Attitude representation 121
A.1 Introduction 121
A.1 Euler angles 121
A.1 Quaternion 123
A.1 Direction Cosine Matrix 125
Appendix B Transformation Matrices Between Reference Frames 128
B.1 OCS to ICS 128
B.1 GCS to ICS 129
B.1 OCS to BCS 130
References 132

11. XI
List of figures
Figure (2-1) Space System.................................................................................. 5
Figure (2-2) TV satellite ..................................................................................... 7
Figure (2-3) GPS satellites.................................................................................. 7
Figure (2-4) Weather Satellites in Geostationary orbit....................................... 8
Figure (2-5) Optical remote sensing satellite...................................................... 9
Figure (2-6) Gravitational force and the centrifugal force acting on bodies
orbiting Earth .................................................................................................... 13
Figure (2-7) apogee ,perigee of the orbit and semi-major axis........................ 14
Figure (2-8) Right ascension of the ascending node......................................... 14
Figure (2-9) Keplerian orbital elements............................................................ 15
Figure (2-10) LEO, MEO and GEO ................................................................. 16
Figure (2-11) GEO satellites appear stationary with respect to a point on Earth
........................................................................................................................... 17
Figure (2-12) Sun synchronous orbit ................................................................ 18
Figure (2-13) Molniya orbit.............................................................................. 19
Figure (3-1) Organization of transferring from one operational mode to another.
........................................................................................................................... 25
Figure (3-2) principle of Earth horizon sensor ................................................. 26
Figure (3-3) Sun sensors ................................................................................... 27
Figure (3-4) Start sensor ................................................................................... 28
Figure (3-5) flux-gate magnetometer................................................................ 29
Figure (3-6) Three degree-of-freedom gyroscope construction geometry. .... 30
Figure (3-7) The QRS11Pro gyro used on Rømer............................................ 31
Figure (3-8) The TELDIX Momentum and Reaction....................................... 33
Figure (3-9) Torque Coils ................................................................................. 34
Figure (3-10) Torque rods................................................................................. 35
Figure (3-11) Torque generated thruster mounted to satellite .......................... 36
Figure (3-12) Sunlight and drag effect.............................................................. 39
Figure (3-13) passive magnetic control orientation profile. ............................. 41
Figure (3-14) spin stabilization......................................................................... 43

12. XII
Figure (4-1) Inertial coordinate system............................................................. 46
Figure (4-2) Greenwich coordinate system....................................................... 46
Figure (4-3) orbital coordinate system.............................................................. 47
Figure (4-4) Body coordinate system................................................................ 48
Figure (4-5) device coordinate system.............................................................. 49
Figure (4-6) Angular motion of rigid body....................................................... 50
Figure (4-7) plane showing regions of stability and instability; adapted
from[12] ............................................................................................................ 66
Figure (5-1) ADCS functional diagram ............................................................ 71
Figure (5-2) Magnetic Torque Direction .......................................................... 72
Figure (5-3) Magnetic Control Torques[23] ..................................................... 73
Figure (5-4)Control torque is always perpendicular to the geomagnetic field
vector................................................................................................................. 74
Figure (5-5) Function diagram of velocity suppression using velocity feed
back algorithm.................................................................................................. 75
Figure (5-6 ) Block diagram of velocity suppression using B-dot technique
No1.................................................................................................................... 82
Figure (5-7 )Block diagram of velocity suppression using B-dot technique No2
........................................................................................................................... 83
Figure (5-8) Bock diagram of velocity suppression using B-dot technique No3
........................................................................................................................... 84
Figure (5-9) Cyclogram of angular velocity suppression algorithm................. 86
Figure (5-10) Satellite angular velocity suppression using angular velocity
feedback ............................................................................................................ 87
Figure (5-11) satellite energy during angular suppression using angular velocity
feedback ............................................................................................................ 87
Figure (5-12) required dipole moment to suppress the satellite angular velocity
using angular velocity feedback........................................................................ 88
Figure (5-13) Satellite angular velocity suppression ....................................... 89
Figure (5-14) satellite energy during angular suppression ............................... 90
31

13. XIII
Figure (5-15) required dipole moment to suppress the satellite angular velocity
........................................................................................................................... 91
Figure (5-16) Function diagram of attitude acquisition and stabilization using
PD-like controller.............................................................................................. 95
Figure (5-17) Block diagram of attitude acquisition and stabilization using
sliding mode.................................................................................................... 100
Figure (5-18 )Block diagram of attitude acquisition and stabilization using
LQR................................................................................................................. 102
Figure (5-19) Cyclogram of attitude acquisition and stabilization algorithm 103
Figure (5-20) Satellite response during angular velocity suppression using
angular velocity feedback, followed by, attitude acquisition and stabilization
using PD-like controller.................................................................................. 104
Figure (5-21) Zoom in for satellite response during angular velocity
suppression using angular velocity feedback, followed by, attitude acquisition
and stabilization using PD-like controller....................................................... 105
Figure (5-22) Required dipole moment during angular velocity suppression
using angular velocity feedback, followed by, attitude acquisition and
stabilization using PD-like controller ............................................................. 106
Figure (5-23) Satellite response during angular velocity suppression using
angular velocity feedback, followed by, attitude acquisition and stabilization
using sliding mode controller.......................................................................... 107
Figure (5-24) Zoom in for satellite response during angular velocity
suppression using angular velocity feedback, followed by, attitude acquisition
and stabilization using sliding mode controller. ............................................. 108
Figure (5-25) Required dipole moment during angular velocity suppression
using angular velocity feedback, followed by, attitude acquisition and
stabilization using sliding mode controller..................................................... 109
Figure (5-26 Satellite response during angular velocity suppression using
angular velocity feedback, followed by, attitude acquisition and stabilization
using LQR....................................................................................................... 110

14. XIV
Figure (5-27) Zoom in for satellite response during angular velocity
suppression using angular velocity feedback, followed by, attitude acquisition
and stabilization using LQR............................................................................ 111
Figure (5-28) Required dipole moment during angular velocity suppression
using angular velocity feedback, followed by, attitude acquisition and
stabilization using LQR .................................................................................. 112
Figure (5-29) S Cyclogram of the developed combined algorithm................ 115
Figure (5-30) Satellite response during angular velocity suppression using
angular velocity feedback, followed by, attitude acquisition and stabilization
using combined algorithm............................................................................... 116
Figure (5-31) Zoom in for satellite response during angular velocity
suppression using angular velocity feedback, followed by, attitude acquisition
and stabilization combined algorithm............................................................. 117
Figure (5-32) Required dipole moment during angular velocity suppression
using angular velocity feedback, followed by, attitude acquisition and
stabilization using combined algorithm.......................................................... 118

15. XV
List of Tables
Table 3-1 Ranges of ADCS sensors accuracy .................................................. 31
Table 5-1initial data used for satellite simulation............................................. 85
Table 5-2the comparison result between angular velocity suppression
algorithms.......................................................................................................... 92
Table 5-3the comparison result between attitude acquisition and stabilization
algorithms........................................................................................................ 113
Table 5-4 the combined algorithms results..................................................... 118

16. XVI
Acronyms
ADCS - Attitude Determination and Control Subsystem
BCS - Body Coordinates System
DCS - Device Coordinates System
FCC Flight Control Center
GCS - Greenwich Coordinates System
OCS - Orbit Coordinates System
MM - Magnetometer
AVM - Angular Velocity Meter
SC - Satellite
SS - Star Sensor
RW - Reaction Wheel
MT - Magnetorquer
LV Lunch Vehicle
RCS Reference Coordinate System
BCS Body Coordinate System
GPS Global Position Satellites
DM - Detumbling mode
SM Standby Mode
IM Imaging Mode
EM Emergency Mode
TM Telemetry Information

17. XVII
List of symbols
a Orbit Semi-Major Axis.
e Orbit Eccentricity
Orbit Right Ascension of The Ascending Node
i Orbit Inclination
W
Argument of The Perigee
fo True Anomaly of The Satellite
coili The Current Passing Magnetic Coil In The
N The Number of Windings In The Coil
A Cross Sectional Area
Relative Permeability
Tgg Gravitational Torque
μ The Gravitational Constant of The Earth
R The Distance Between Satellite Center of Mass And Earth
Center of Mass
J The Moment of Inertia Tensor For The Satellite
Deviation Angel From The Nadir Pointing
mT The Magnetic Torque
D Vector of Total Satellite Magnetic Dipole
B Earth Geomagnetic Field Vector
psc The Center of Pressure
SpT Solar Radiation Torque
So Solar Constant
c Speed of Light
si The Angle of Sun Light Incidence
cg The Center of Gravity
q The Surface Reflectance Factor
adT Aerodynamic Torque
The Density

18. XVIII
cD The Coefficient of Drag
vc The Orbital Velocity
IZ Z Axis of ICS
IY Y Axis of ICS
IX X Axis of ICS
gZ Z Axis of GCS
gY Y Axis of GCS
gX X Axis of GCS
OZ Z Axis of OCS
OY Y Axis of OCS
OX X Axis of OCS
DZ Z Axis of DCS
DY Y Axis of DCS
DX X Axis of DCS
w The Angular Velocity of Rotating Co-Ordinate System With
Respect To ICS
H The Satellite Angular Momentum
a Acceleration
extT Sum of External Torques Acting On The Satellite
disT Total External Disturbance Torque
cT Control Torque
Satellite Absolute Angular Velocity
y Satellite Relative Angular Velocity
B
IA Transformation Matrix From ICS To BCS
wH The Angular Momentum of The Wheels
O
The Orbit Rate
er The 3rd
Column In The Rotation Matrix From OCS To BCS

19. XIX
Quaternion Describes The Orientation of BCS With Respect
To OCS
0 Scalar Part of Quaternion
Vector Part of Quaternion
Y The Instantaneous Angular Velocity of The Satellite In
Quaternion Form
F Input Matrix For Control
U Vector of Input Control Torque
X State Vector
L Dipole Moment
m Mass
f Force
Me Earth Mass
G The Universal Gravitational Constant
e Earth Rotation Velocity
KinE Kinetic Energy
ggE Potential Energy Associated With The Gravity Gradient
gyroE Potential Energy Due To The Revolution of The Satellite
About The Earth
totE Total Energy
V Lyapunov Candidate Function
Way Angel That Describe The Rotation About Z Axis
Roll Angel That Describe The Rotation About X Axis
Pitch Angel That Describe The Rotation About Y Axis
m
kR Rotation Matrix From k Coordinate System To m Coordinate
System
[R] Direction Cosine Matrix
Quaternion Multiplication
The Angle Between The Line of Aries And Greenwich Line

20. Chapter1 Introduction
1
CHAPTER (1)
INTRODUCTION
Remote sensing satellites are used to observe features on the ground, the
behavior of the oceans, or the characteristics of the atmosphere from space.
Observation instruments are installed on satellites for remote sensing purposes.
That satellite has the advantage of being able to give up-to-date information
(satellite remote sensing can be programmed to enable regular revisit to object
or area under study) , observe wide areas, with good spectral resolution and it
give continuous acquisition of data. Data collected by the satellites are
transmitted to ground stations where images of earth's surface are reconstituted
to obtain the required information.
In order to help the satellite to keep continues earth observation and
nadir pointing all over its life time starting from in orbit injection, attitude
determination and control subsystem (ADCS) is used to provide the required
pointing accuracy.
ADCS uses different types of sensor to determine or estimate the current
attitude of satellite such as; star sensor, sun sensor, earth sensor, magnetometer
and gyros. In addition it used different type of actuators to keep continues
observation of earth against the external disturbances such as; magnetorqure,
thruster and momentum exchange devices.
Since the satellite needs different pointing requirements all over its
mission life time, starting from separation from launcher , high accurate nadir
pointing during imaging periods, passing with low accuracy pointing intervals

21. Chapter1 Introduction
2
during non imaging periods. Therefore ADCS operation is divided into
different operation modes. These modes are, angular suppression or detumbling
mode (DM), which, is used to suppress the high angular velocity obtained due
to separation from launcher. Non imaging mode or Standby Mode (SM) where
the main target is to save the system resources (i.e. power and devices life time)
Imaging mode (IM), where high accurate pointing is needed for the purpose of
earth imaging. Finally in any case of failure for sensor or actuator, ADCS will
enter emergency mode (EM) to diagnose the failure reason.
There are different techniques to apply control torque for disturbance
compensation and to maintain the required orientation. For these purposes, two
types of control techniques are often employed, passive and active control.
Because Attitude control system is highly mission dependent, so the decision to
use a passive or an active control technique or a combination of them depends
on mission pointing and stabilization requirements. Since for imaging remote
sensing satellite three axes attitude stabilization is needed, so active control will
be used.
The main trend now for satellite design, is to achieve low cost, weight
and power satellite. Since magnetic actuators and sensors are considered as
lowest cost ,weight and power device used in satellite attitude control, that is
why they are used now widely used in three axis attitude control in designing
of new satellites such as CITCH, Oresat ,SunSat and EgyptSat1
Magnetic actuators are suitable in practice for low Earth orbit (LEO)
satellites. Such actuators operate on the basis of the interaction between a set of
three orthogonal, current-driven magnetic coils and the magnetic field of the
Earth (Wertz, 1978; Sidi, 1997) and therefore provide a very simple solution to
the problem of generating torques on board a satellite. The major drawback of
this control technique is that the torques which can be applied to the satellite

22. Chapter1 Introduction
3
for attitude control purposes are constrained to lie in the plane orthogonal to the
magnetic field vector. In particular, three axes magnetic stabilization is only
possible if the considered orbit a variation of the magnetic field which is
sufficient to guarantee the stability of the satellite (Bhat & Dham, 2003).
For angular suppression phase commonly two types of control are used,
angular velocity feedback and B-dot technique, but for attitude acquisition and
attitude stabilization state (i.e. angular velocity and quaternion) feedback, linear
quadratic regulator and sliding mode controllers are used.
In this thesis, a comparison study between the above mentioned
controllers is made in the corresponding operation modes, taking into account
the following parameter as comparison criteria
Settling time
Steady stat error
Required dipole moment
Required calculation time for one cycle of the used control algorithm
Cost
The comparison study showed that each one of the above mentioned
algorithms has advantage and disadvantages referring to the comparison
parameters, the motivation here is to develop a combined control algorithm that
assembles the advantages of these different controllers, according to the
corresponding operation mode.
A Simulation was done for the developed controller and compared with
the previous mentioned control algorithm during all operation modes.
Outline of Thesis
Chapter 2 gives introduction about the satellite. Architecture of satellite
was presented where the different application of satellite payload and the main
satellite subsystems were described. In addition to the different types of
satellite orbits was discussed

23. Chapter1 Introduction
4
Chapter 3 focuses on attitude determination and control subsystem. The
internal influence between ADCS and other satellite subsystem was discussed.
Then ADCS tasks and operational modes for remote sensing satellite were
described. In addition, the extern environments disturbances that affect ADCS
operation were introduced. More over the principle of operation for commonly
used sensors and actuators for ADCS were introduced. Finally the different
control techniques used in ADCS were briefly discussed
Chapter 4 provides definitions of coordinate systems used throughout
the thesis. Detailed description of the satellite motion is given, and linearized
model for the satellite dynamics/kinematics was introduced finally the model of
satellite motion in orbit was presented
Chapter 5 discusses the magnetic control problem. First, the
controllability and stability of magnetic actuated satellite was described, and
then the commonly used control algorithms were introduced. The development
of the combined algorithm was discussed in details. Finally A complete
simulation for full scenario of ADCS operation mode was applied for specified
satellite parameter. The results are compared for the commonly used controller
and the combined controller
Chapter 6 concludes this thesis. It summarizes the results and suggests
areas for further research.

24. Chapter2 Space Segment Overview
5
CHAPTER (2)
SPACE SEGMENT OVERVIEW
2.1 Space System Composition
The block diagram of a space system is shown in Figure (2-1). Space
system can be broken down into three main physical parts; the space segment,
the launch segment, and ground segment. The space segment may be a single
satellite or a constellation of satellites. The satellite contains the payloads that
will accomplish the main mission, as well as the satellite bus that provides the
supporting services for operation of the payload. The launch segment is the
launch vehicle which injects the satellites into its orbit. The ground segment
consists of gateways where the commands are up linked to satellite and data
(i.e. health of satellite and payload data) is down linked from satellites as well
as processing and distribution facilities to put the raw data in the appropriate
form and location for users.[1]
Figure (2-1) Space System
Space System
Space
Segment
Launch
Segment
Ground
Segment

25. Chapter2 Space Segment Overview
6
2.2 Satellite Architecture
In general, space segment consists of the satellite; with its main two
parts, the payload and the satellite bus. The satellite bus comprises the other
supporting subsystems whose functions needed to allow the satellite to perform
its mission. Examples of those subsystems are attitude and orbit control, power
generation and data handling. The Payload Module houses the payload sensors,
the facilities needed for data handling and interfaces with satellite subsystems
[2].
2.2.1 Satellite Payload
The payload is dependent upon the mission of the satellite, and is
typically regarded as the part of the satellite "that pays the bills". Typical
payloads are listed below.
2.2.1.1 Communication
Communication satellites provide broadcast (i.e. DirecTV) or point-to-
point (i.e. Iridium) communication services to users around the globe, as well
as data and voice relay between satellite in orbit and controllers on the ground
(i.e. TDRSS). Broadcast missions typically have a set region on the Earth, to
which they are broadcasting, and typically utilization geostationary orbits and a
single satellite to cover a single region, or four satellites in GEO to provide
worldwide broadcast coverage, see Figure (2-2). Point-to-point missions are
typically accomplished with either one or several GEO satellites (like the
broadcast mission).Communication missions that relay data between space and
the Earth typically use GEO satellites.
2.2.1.2 Positioning and Navigation
Positioning and navigation (POS/NAV) missions typically provide near
global coverage and use triangulation as a strategy to provide the POS/NAV
service. Thus, multiple satellites need to be in view of a ground receiver at any
point in time, leading architects to use MEO orbits. Currently, the U.S. fields

26. Chapter2 Space Segment Overview
7
GPS, and the Russians field Glonass. The European community is in the
planning stages of their Galileo POS/NAV satellite system, and will likely field
it later this decade.
Figure (2-2) TV satellite
Figure (2-3) GPS satellites
2.2.1.3 Weather
Weather satellites are referred to as the third eye of meteorologists, as
the images provided by these satellites are some of the most useful sources of
data for them. Satellites measure the conditions of the atmosphere using
onboard instruments. The data are then transmitted to the collecting centers
where they are processed and analyzed for varied applications.

27. Chapter2 Space Segment Overview
8
All the weather satellites are placed into either of the two types of orbits
around the Earth, namely the polar sun-synchronous low Earth orbit and the
geostationary orbit (GEO) Figure (2-4). Polar orbit weather satellites, due to
their low altitudes, have better spatial resolution as compared to the GEO
satellites Hence they help in a detailed observation of the weather features like
the cloud formation, wind direction, etc. However, these satellites have a
poorer temporal resolution, visiting a particular location only one to four times
a day. Hence, only a few weather satellite systems have satellites in these
orbits. Most weather satellites employ a geostationary orbit as it offers better
temporal resolution as compared to that provided by the polar satellites.
Geostationary weather satellites are the basis of the weather forecasts that are
seen on television [3]
Figure (2-4) Weather Satellites in Geostationary orbit
2.2.1.4 Remote Sensing
Remote sensing satellite is used for acquiring information about the
Earth's surface by sensing reflected or emitted energy by the Earth's surface
with the help of sensors on board the satellite. Based on the source of radiation,
remote sensing can be classified to passive and active.
Passive remote sensing refers to the detection of reflected solar
radiation by the objects on the Earth or the detection of thermal or microwave
radiation emitted by them. The most common passive sensors are imaging
sensors include multi-spectral and panoramic cameras .Camera systems are

28. Chapter2 Space Segment Overview
9
optical sensors that use a system of lenses to form an image of Earth’s surface
due to the detected radiation at the focal plane of the camera.
Active remote sensing involves the use of active artificial sources of
radiation which mounted on board the satellite. These sources comprise both a
transmitter as well as a receiver. The transmitter emits electromagnetic
radiation of a particular wavelength band, depending upon the intended
application. The receiver senses the same electromagnetic radiation reflected or
scattered by the ground. One of the most common active sensors used is the
synthetic aperture radar (SAR). In SAR imaging, microwave pulses are
transmitted by an antenna towards the Earth's surface and the energy scattered
back to the satellite is measured SAR makes use of the radar principle to form
an image by utilizing the time delay of the backscattered signals.
Figure (2-5) Optical remote sensing satellite
2.2.2 Satellite Bus
Here we will briefly summarize satellite bus subsystems. These
subsystems support payload mounting, correct pointing of the payload, and
maintain payload in the right orbit. Besides, receiving commands from ground,
forming and transmitting telemetry to FCC, and provide data storage and
communications. Also, provide the required electric power and control the
payload temperature.

29. Chapter2 Space Segment Overview
10
2.2.2.1 The Structural Subsystem
The structural subsystem carries, supports, and mechanically aligns the
satellite equipment. It also cages and protects folded components during boost
and deploys them in orbit. The main load-carrying structure or primary
structure is sized by either the strength needed to carry the satellite mass
through launch accelerations and transient events during Launch or stiffness
needed to avoid dynamic interaction between the satellite and the launch
vehicle structures. Secondary structure, which consists of deployable and
supports for components is designed for compact packaging and convenience
of assembly. [4]
2.2.2.2 Attitude Determination and Control Subsystem
The attitude determination and control subsystem measures and controls
the satellite's angular orientation (pointing direction).The simplest satellite are
either uncontrolled or achieve control by passive methods such as spinning or
interacting with the Earth's magnetic or gravity fields. These may or may not
use sensors to measure the attitude or position. More complex systems employ
controllers to process the satellite attitude information obtained from sensors
and actuators torquers to control attitude, velocity, or angular momentum. SC
may have several bodies or appendages, such as solar array or communication
antennas, that required certain direction pointing. The complexity of the
attitude control subsystem depends on the number of body axes and appendage
to be controlled, control accuracy, and speed of response, maneuvering
requirements and the disturbance environment. [4]
2.2.2.3 Propulsion Subsystem
Propulsion subsystem is used to change orbital parameters in order to
transfer from one orbit to another, maintain the satellite in the required orbit all
over its life time. In addition it is also used in attitude maneuver and
stabilization against environmental disturbance forces (e.g. drag), correct
satellite angular momentum and satellite attitude control. The equipment in the

30. Chapter2 Space Segment Overview
11
propulsion subsystem includes a propellant supply (propellant, tankage,
distribution system, pressurization and propellant controls) [4].
2.2.2.4 Communications Subsystem
The communications subsystem links the satellite with the ground or
other satellite. Information sent to the satellite (i.e. uplink or forward link),
consists of commands and needed data to satellite (i.e. satellite control
commands and new SW version). Information received from the satellite (i.e.
downlink or return link) consists of satellite status telemetry and payload data.
The basic communication subsystem consists of a receiver, a transmitter, and a
wide-angle (hemispheric or omni-directional) antenna. Systems with high data
rates may also use a directional antenna [4].
2.2.2.5 Command and Data Handling Subsystem
The command and data handling subsystem distributes commands to
assigned subsystems. It also stores data from the satellite and payload. For
simpler systems, we combine these functions with the communications
subsystem as a tracking, telemetry, and command subsystem. This arrangement
assumes that distributing commands and formatting telemetry are base upon
extensions of communications modulation and demodulation. In its more
general structure, it comprises a central processor (computer), data buses,
remote interface units, and data storage units to implement its functions. It may
also handle sequenced or programmed events [4].
2.2.2.6 Power System
Satellites must have a continuous source of electrical power-24 hours a
day, 365 days a year. The two most common power sources are high
performance batteries and solar cells. Solar cells are an excellent power source
for satellites. They are lightweight, resilient, and over the years have been
steadily improving their efficiency in converting solar energy into electricity.
There is however, one large problem with using solar energy. If solar energy

31. Chapter2 Space Segment Overview
12
were the only source of power for the satellite, the satellite would not operate
during eclipse period. To solve this problem, batteries are used as a
supplemental on-board energy source. Initially, Nickel-Cadmium batteries were
utilized, but more recently Nickel-Hydrogen batteries have proven to provide
higher power, greater durability, and the important capability of being charged
and discharged many times over the lifetime of a satellite mission. [5]
2.2.2.7 The Thermal Subsystem
The thermal subsystem controls the satellite equipment's temperatures.
Normally thermal control is done through either passive or active techniques.
In passive control, It does so by the physical arrangement of equipment, using
thermal insulation and coating. This is done to balance heat from power
dissipation, absorption from the Earth and Sun, and other radiation sources in
the space. Sometimes passive, thermal-balance techniques are not enough. In
this case, active control in the form of electrical heaters, high-capacity heat
conductors, and/or heat pipes, are employed [4].
2.3 Satellite Orbits
After a satellite is separated from launching vehicle, it moves in a path
around the Earth called an orbit. Satellite orbiting Earth due to the balance
between two forces, gravitational force which attracts the satellite towards the
Earth and centrifugal force (due to linear velocity of the satellite in orbit )
which causes repulsion of the satellite out from Earth [3],see Figure (2-6.)
During satellite mission design, the orbit is chosen which is appropriate to its
mission. So, a satellite that is in a very high orbit will not be able to see objects
on Earth as many details as orbits that are lower, and closer to the Earth's
surface. Similarly, the satellite velocity in orbit, the areas observed by the
satellite, and the frequency with which the satellite passes over the same
portions of the Earth are all important factors in satellite orbit selection.
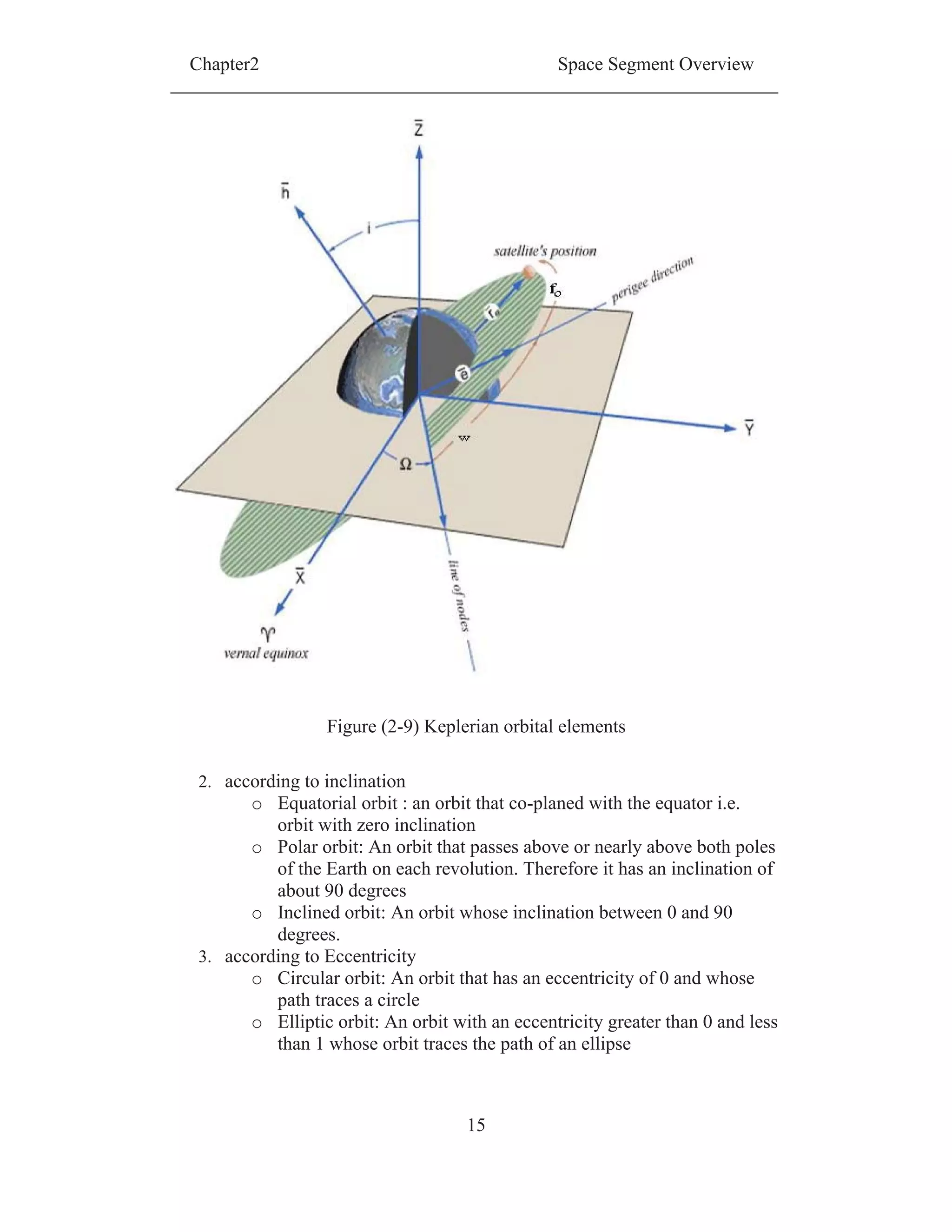
Essentially, there are six orbital parameter called classical Keplerian orbital
elements define the orbit as shown in Figure (2-8) [5].

32. Chapter2 Space Segment Overview
13
Figure (2-6) Gravitational force and the centrifugal force acting on bodies
orbiting Earth
1. Semi-major axis. a This is a geometrical parameter of the elliptical
orbit. It can, however, be computed from known values of apogee and
perigee distances as [3], for definition of apogee and perigee see Figure
(2-7).
2
perigeeapogee
a (2.1)
2. Eccentricity.e The orbit eccentricity is the ratio of the distance between
the centre of the ellipse and its focus to the semi-major axis of the
ellipse [3] see Figure (2-7).
3. Right ascension of the ascending node . it tells about the orientation of
the line of nodes, which is the line joining the ascending and descending
-nodes, with respect to the direction of the vernal equinox [3] See
Figure (2-8).
Vernal equinox is the line that intersects the Earth's equatorial plane and
the Earth's orbital plane, which passes through the centre of the Earth with
respect to the direction of the sun on 21 March [3].
4. Inclination i . is the angle that the normal to the orbital plane of the
satellite makes with the normal to the equatorial plane [3] , Figure (2-9).
5. Argument of the perigee W. This parameter defines the location of the
major axis of the satellite orbit. It is measured as the angle between
the line joining the perigee and the focus of the ellipse and the line of

33. Chapter2 Space Segment Overview
14
nodes in the same direction as that of the satellite orbit [3], see Figure
(2-9).
6. True anomaly of the satellite fo. This parameter is used to indicate the
position of the satellite in its orbit. It is defined as the angle, between the
line joining the perigee and the centre of the Earth with the line joining
the satellite and the centre of the Earth [3], see Figure (2-9)
Orbits can be classified according to different criteria [3], such as
1. According to orbit Altitude
o Low Earth Orbit (LEO): orbit altitude ranging in altitude from
200–1000 km
o Medium Earth Orbit (MEO): orbit altitude ranging from 1000 km
to just below geosynchronous orbit at 35786 km.
o High Earth Orbit (HEO): orbit altitude above 35786 km.
(a) (b)
Figure (2-7) apogee ,perigee of the orbit and semi-major axis
Figure (2-8) Right ascension of the ascending node

34. Chapter2 Space Segment Overview
15
Figure (2-9) Keplerian orbital elements
2. according to inclination
o Equatorial orbit : an orbit that co-planed with the equator i.e.
orbit with zero inclination
o Polar orbit: An orbit that passes above or nearly above both poles
of the Earth on each revolution. Therefore it has an inclination of
about 90 degrees
o Inclined orbit: An orbit whose inclination between 0 and 90
degrees.
3. according to Eccentricity
o Circular orbit: An orbit that has an eccentricity of 0 and whose
path traces a circle
o Elliptic orbit: An orbit with an eccentricity greater than 0 and less
than 1 whose orbit traces the path of an ellipse

35. Chapter2 Space Segment Overview
16
2.3.1 Special Orbits
An important consideration in space mission design is determining the
type of Earth Orbit that best suits the design goals and purpose of the mission.
A brief description for the special orbits which frequently used such as; low
Earth orbit, medium Earth orbit, geostationary orbit, polar orbit, Sun-
synchronous orbit and Molniya orbit, is presented.
2.3.1.1 Low Earth Orbit (LEO)
Orbiting the Earth at roughly 200-1000 Km altitude [6]: Almost 90
percent of all satellites in orbit are in LEO [6]. LEO is often utilized because of
the low launch requirements that are needed to place a satellite into orbit. LEO
satellites orbit the Earth in roughly 90 minute periods. This means that they are
fast moving, and sophisticated ground equipment must be used to track the
satellite, LEO is used for such missions as flight tests, Earth observations,
astronomical observations, space stations and scientific experiments [8], [6].
Figure (2-10) LEO, MEO and GEO
2.3.1.2 Medium Earth Orbit (MEO)
MEO sometimes called Intermediate Circular Orbit (ICO), is the region
of space around the Earth above low Earth orbit (1,000 kilometers) and below
geostationary orbit (35,786 Km).The most common use for satellites in this

36. Chapter2 Space Segment Overview
17
region is for navigation, such as the GPS (20,200 Km) and Galileo
(23,222 Km) constellations. Communications satellites that cover the North and
South Pole are also put in MEO [6]. The orbital periods of MEO satellites
range from about 2 o 12 hours. Telstar, one of the first and most famous
experimental satellites, orbited in MEO [9]
2.3.1.3 Geostationary/Geosynchronous Earth Orbit (GEO)
Satellite in geostationary orbit appears to remain in the same spot in the
sky all the time. Really, it is simply traveling at exactly the same speed as the
Earth is rotating below it, but it looks like it is staying still regardless of the
direction in which it travels, east or west. A satellite in geostationary orbit is
very high up, at 35,850 km above the Earth. Geostationary orbits, therefore, are
also known as high orbits; GEO is used for communications satellite
Figure (2-11) GEO satellites appear stationary with respect to a point on Earth
2.3.1.4 Polar Earth Orbit
For full global coverage of the Earth, a ground track would have to
cover latitudes up to 90o
. The only orbit that satisfies this condition has an
inclination of 90°. These types of orbits are referred to as polar orbits. Polar
orbits are used extensively for the purpose of global observations.

37. Chapter2 Space Segment Overview
18
2.3.1.5 Sun Synchronous Orbits (SSO)
A Sun-synchronous orbit (SSO) is a nearly polar orbit where the
ascending node precesses at 360 degrees per year or 0.9856 degrees per day.
SSO orbital plane has a fixed orientation with respect to the_Earth-sun
direction and the angle between the orbital plane and the Earth-sun line remains
constant throughout the year as shown in Figure (2-12), so this type of orbit
assures that the local solar time (LST) at the ascending node is nearly constant
throughout the life of the mission. Satellites in sun-synchronous orbits are
particularly suited to applications like passive remote sensing, meteorological
and atmospheric studies,[6].
Figure (2-12) Sun synchronous orbit
2.3.1.6 Molniya Orbit
Highly eccentric, inclined and elliptical orbits are used to cover higher
latitudes, which are otherwise not covered by geostationary orbits. A practical
example of this type of orbit is the Molniya orbit. It is a widely used satellite
orbit, used by Russia and other countries of the former Soviet Union to provide
communication services. Typical eccentricity and orbit inclination figures for
the Molniya orbit are 0.75 and 65° respectively. The apogee and perigee points
are about 40000 km and 400 km respectively from the surface of the Earth. It
has a 12-hour orbit and a satellite in this orbit remains near apogee for

38. Chapter2 Space Segment Overview
19
approximately 11 hours per orbit [4] before diving down to a low-level perigee.
Usually, three satellites at different phases of the same Molniya orbit are
capable of providing an uninterrupted service.
Figure (2-13) Molniya orbit

39. Chapter3 Attitude Determination
and Control Subsystem
20
CHAPTER (3)
ATTITUDE DETERMINATION AND CONTROL
SUBSYSTEM ADCS
In this chapter more detailed explanation about ADCS is introduced.
The impact of other subsystems requirements on ADCS and impact of ADCS
requirements on the other subsystems are presented. In addition, the tasks that
ADCS must perform all over the satellite lifetime and the ADCS operational
modes are describe. Then, an illustration for the physical concepts and
functions of ADCS devices such as sensors and actuators are exhibited.
Besides, different disturbances affecting rotational motion of the satellite are
demonstrated. Finally, the general control methods applied with ADCS are
presented. The control methods and
3.1 Internal influence between satellite mission and other subsystems
upon ADCS
ADCS is very closely coupled with other subsystems; it is interactively
influences and being influenced by other satellite’s subsystems. In the
following section, a briefer description for interaction between ADCS and
other subsystem is presented.
3.1.1 Internal influence between ADCS and Mission requirement
Main mission of the satellite imposes the main requirements on ADCS.
Normally, the requirements associated with the mission are
Earth pointing or inertial pointing ( this will affect in ADCS control
techniques)

40. Chapter3 Attitude Determination
and Control Subsystem
21
Accuracy /stabilization requirements (this will affect in accuracy of
selected ADCS sensors).
Slewing requirements (this will affect in selection of actuators types)
Mission life time (this will affect in life time of selected ADCS devices)
Orbit parameters (this will affect in the magnitude of environment
disturbance which will perturb ADCS)
3.1.2 Internal influence between ADCS and Structure Subsystem
The ADCS Subsystem directly interacts with the structure subsystem.
The structure of the satellite affects the space craft moment of inertia and
location of its center of mass, which is affecting the dynamics and stability of
the satellite. Also, the rigidity of the structure determines whether the model of
the satellite will be a rigid body or a flexible one. In addition, mounting
accuracies of ADCS devices are one of the main constrains upon the structural
design of the satellite.
3.1.3 Internal influence between ADCS and Power Subsystem
The ADCS and the power subsystem are influencing each other. The
power budget of the satellite must take into account the requirements of the
ADCS sensors and actuators during different operational modes. For satellite
using solar panels, there are additional pointing requirements placed on the
ADCS, if solar panels must be kept aligned with the Sun for optimal
performance
3.1.4 Internal influence between ADCS and Communication Subsystem
If the satellite antenna is required to be pointed within a given accuracy
in order to communication with ground station, the Communication subsystem
will add pointing requirements on the ADCS Subsystem during communication
session.

41. Chapter3 Attitude Determination
and Control Subsystem
22
3.1.5 Internal influence between ADCS and Command and Data
Handling Subsystem
Since the Command and data handling subsystem is the main brain that
organizes the data flow between satellite subsystems; so it imposes
requirements on the volume and rate of data transfer to ADCS or from ADCS
to other subsystems.
3.1.6 Internal influence between ADCS and thermal subsystem
In order to keep temperature of the satellite’s components within
specific range the thermal subsystem may impose maneuver requirements on
ADCS, by pointing the hot side to deep space and pointing the cold side
towards the sun
3.2 ADCS Tasks
According to the previous mutual impacts of ADCS with other
subsystems, ADCS has the following tasks must to be executed all over the
satellite life time. That is, ADCS executing the following tasks from the
moment of separation up to de-orbiting or discarding of the mission.
1. Damping the satellite angular velocity, obtained from LV after satellite
separation.
2. Attitude acquisition of the satellite where the BCS is oriented to be
coincide with the assigned RCS (in Earth observation missions OCS will
be this RCS). In this attitude acquisition the satellite is initially oriented
towards the RCS supports the mission requirements.
3. The satellite three-axis stabilize in the RCS with the required accuracy
during the imaging sessions.
4. Three-axis stabilization in nadir pointing with low accuracy during non-
imaging periods
5. Attitude determination with the required accuracy during all ADCS
operational modes

42. Chapter3 Attitude Determination
and Control Subsystem
23
3.3 Satellite operational modes
According to the above required tasks from ADCS, the ADCS
operational mode will be.
3.3.1 De-tumbling mode (DM)
This mode occurs after the satellite is released from the LV or after
loosing of orientation due to any failure. During this mode the ADCS suppers
the satellite angular velocity that received from the LV, Because of power
limitation this process should be completed within specified period.
3.3.2 Standby Mode (SM)
After DM satellite can have arbitrary attitude Automatically so after
finishing DM, ADCS transfers to SM in order to make attitude acquisition of
satellite (i.e. Orient the satellite BCS to be co-onside with OCS to get
stabilization at nadir pointing with low accuracy) and stay in this case
whenever there is no imaging tasks assigned to the satellite. In this mode the
satellite attitude should be kept even with a low accuracy to avoid loosing the
satellite’s attitude, it is a low accuracy mode. In this mode, the most important
thing is to save the system resources (i.e. lifetime of ADCS devices) and reduce
the consumed power. ADCS stay in SM about 95% of the whole satellite
lifetime
3.3.3 High Accuracy Mode (HAM) or Imaging Mode (IM)
In this mode, ADCS should provide the required control to achieve the
pointing of the payload requirements. As an example, for imaging remote
sensing satellite using magnetic actuator the satellite must be stabilized at nadir
with high accuracy during imaging periods, so this mode called imaging mode
(IM)..

43. Chapter3 Attitude Determination
and Control Subsystem
24
3.3.4 Emergency Mode (EM)
In case of any failure in ADCS (e.g. loosing satellite attitude or any
failure of ADCS devices ) ADCS automatically transfer to EM .In this mode
ADCS switch off all ADCS devices and make diagnostic for ADCS devices
according to command from ground and send TM to ground in order to take
the suitable decision.
3.3.5 Transferring from one operational mode to another
The organization of transfer from one mode to another is shown in
Figure (3-1).ADCS operational cyclogram and conditions for transferring
between modes are as follows:
1. After separation from LV and starting of satellite operation ADCS
enters DM.
2. When DM is finished, ADCS directly transfers the satellite to SM and
stay in SM.
3. Before imaging time, within specified period (i.e. Period sufficient to
stabilize the satellite at the required attitude with the required
accuracy),ADCS transfers the satellite to IM.
4. After finishing of imaging task, ADCS transfers the satellite again to
SM
5. In normal cases, the sequence of items 3-4 are repeated.
6. In case of any failure (i.e. failure in ADCS devices or attitude
orientation ), ADCS directly transfers the satellite to EM.

44. Chapter3 Attitude Determination
and Control Subsystem
25
Figure (3-1) Organization of transferring from one operational mode to
another.
3.4 ADCS devices
A satellite in space must point to a given direction as assigned by the
mission requirements. Many satellites are Earth orientated while others are
inertial space object oriented such as sun or a star of interest. The orientation
of the satellite in space is known as its attitude. In order to achieve control and
stabilization of the satellite, attitude sensors are used to determine the current
attitude and actuators are used to generate required torque to maintain the
required attitude. This section gives brief description of the most common
used ADCS sensors and actuators.
3.4.1 ADCS Sensors
Sensors generally determine the attitude and pointing direction of
satellite with respect to reference objects, this object could be inertial space or a
body of known position. The most commonly used reference objects, Earth,
Sun, stars, geomagnetic field and inertial space.
DM
finishing
ADCS
failure
DM SM IM
EM
Imaging
command
Finishing imaging
session
ADCS
failure
ADCS
failure
Fixing of ADCS
failure

45. Chapter3 Attitude Determination
and Control Subsystem
26
3.4.1.1 Earth’s Horizon sensor
For near-Earth satellites the Earth covers a large proportion of the sphere
of view and presents a large area for detection. The presence of the Earth alone
does not provide a satisfactory attitude reference hence the detection of the
Earth’s horizon is widely used.
Horizon sensor is infrared device that detect the contrast between the
cold of deep space and the heat of the Earth’s see Figure (3-2). Horizon sensors
can provide pitch and roll attitude knowledge for Earth-pointing satellite. For
the better accuracy in low Earth orbit (LEO), it is necessary to correct the data
for the Earth oblateness and seasonal changes in the apparent horizon
[10].Earth’s Horizon sensor is used in AEROS-I,-2, MAGSAT, SEASAT [15].
Figure (3-2) principle of Earth horizon sensor
3.4.1.2 Sun sensor
Sun sensor is widely used with satellite mission due to the special
features of sun as a space object. One of these features is the brightness of the
sun, which makes it easy to be distinguished among other solar and stellar
objects. also the Sun-Earth distance makes it appear as nearly a point source
(0.25 º). Those factors urge ADCS designer to rely upon sun sensors in high
pointing accuracy missions.

46. Chapter3 Attitude Determination
and Control Subsystem
27
Sun sensor measures one or two angles between their mounting base
and incident sunlight. Categories of sensors are ranging from just sun presence
detector, which detects the existence of sun, rather accurate analogue sensor
measuring sun incidence angle, up to high accuracy digital instrument, which
measure the sun direction to accuracy down to one arc-minute. Typical digital
sun sensor is shown Figure (3-3).
Sun sensor is accurate and reliable, but require direct line of sight to the
sun. Since most low-Earth orbits include eclipse periods, the attitude
determination system should provide some way of handling the regular loss of
Sun vision. Sun sensor is used in AEROS-1,2 , GEOS-3, MAGSAT, SAGE,
SEASAT [15].
Figure (3-3) Sun sensors
3.4.1.3 Star mapper
Star mapper provides the most accurate absolute pointing information
possible for a satellite attitude. It contains Charged-Coupled Device (CCD)
sensors or Active Pixel Sensors (APS) which provides a relatively inexpensive
way to image the sky. It extracts information about satellite attitude by
mapping the obtained stars image with the stored stars pattern catalog. Any

47. C
orie
corr
thre
suff
fram
velo
sen
imp
iden
MA
3.4.
dire
requ
attit
Nav
mag
pos
Chapter3
entation of
responding
ee stars on
ficient to d
me of refe
ocities of t
sor.
The a
possible wi
ntification.
AGSAT [15
.1.4 Magn
Magne
ection and
uire comp
tude deter
vigational
gnetic fiel
sition. Com
f satellite w
g star patte
n the senso
determine
erence. Th
the satellit
accuracy a
ithout high
. Star sen
5].
netometers
etometers a
magnitud
plex softw
rmination
informatio
d to app
mparison be
will detecte
ern as show
or, along w
the attitud
he star cam
te as this c
Figu
and autono
h-speed mi
nsor is us
s
are simple
e of the E
ware for in
as comp
on are use
proximate
etween me
28
d as a shift
wn in Figu
with their lo
de of the c
mera is ge
causes a sm
ure (3-4) S
omy provi
icroprocess
sed in AT
, lightweig
Earth’s mag
nterpretatio
pared to
ed with a
the field d
easured and
A
a
ft between t
ure (3-4).
ocations in
camera wi
enerally se
mearing of
Start sensor
ided by a
sors for im
TS-6, Egy
ght sensors
gnetic fiel
on and pr
horizon, s
a computer
direction a
d calculate
Attitude De
and Contro
the imaged
The locati
n inertial c
ith respect
ensitive to
f the star i
r
star cam
mage proce
yptsat-1, L
s that mea
d. They ar
rovide rela
sun, and
r model o
at the sate
ed earth ma
eterminatio
l Subsystem
d stars and
ons of at l
coordinates
to an ine
large ang
images on
mera would
essing and
LANDSAT
asure both
re reliable
atively co
star sens
of the Ear
ellite’s cur
agnetic fiel
on
m
d the
least
s are
ertial
gular
n the
d be
star
T-D·,
the
but
oarse
sors.
rth’s
rrent
ld is

48. Chapter3 Attitude Determination
and Control Subsystem
29
used to provide information about satellite orientation. Employing estimation
techniques such as Kalman filter, allows magnetometer to work as standalone
device for attitude determination [11]. The Earth’s magnetic field also varies
with time and can't be calculated precisely, so a magnetometer is often used
with another sensor such as a sun, horizon or star sensor or a gyroscope in
order to improve the accuracy. Magnetometer is used in AEROS-1, Egyptsat1,
GEOS-3, SEASA [15].
Figure (3-5) flux-gate magnetometer
3.4.1.5 Inertial Sensor or Gyro
By definition, a gyroscope, is any instrument, which uses a rapidly
spinning mass to sense and respond to changes in the inertial orientation of its
spin axis. There are types of attitude sensing gyros: mechanical and optical
gyro. These sensors measure satellite orientation change.
Mechanical Gyroscopes
The angular momentum of a gyro, in the absence of an external torque,
remains constant in magnitude and direction in space. Therefore, any rotation
of the satellite about the gyro's input axis results in a precession of the gimbal

49. Chapter3 Attitude Determination
and Control Subsystem
30
about the output axis. Figure (3-6) shows the basic principles of how
mechanical gyros operate
Figure (3-6) Three degree-of-freedom gyroscope construction geometry.
Optical Gyroscopes
Optical gyros are gyroscopes that utilize a light ring instead of a
mechanical rotor as the main component to determine rotational changes. All
optical gyros work on the same principle, the Sagnac effect, This effect works
on relativistic principles but can be described in "normal" terms. Two light
beams are traveling through circular paths of the same length but in opposite
directions around in an optical coil. If the optical coil is rotating, one of the
light beams will take a longer period of time to travel the circumference of the
coil. This time lag is measured and converted into a rotational rate for the coil.
Thus, the rotation the gyro is feeling can be measured. The length changes
associated with the light beam are of nuclear dimensions and are difficult to
measure. However, great accuracy can be achieved through the use of this type

50. Chapter3 Attitude Determination
and Control Subsystem
31
of gyroscope. The most common devices of this type is the Ring Laser Gyro
(RLG) and Fiber Optic Gyros (FOG) .Gyros are used in ATS-6,
Egyptsat1,LANDSAT-D·, MAGSAT [15].
Figure (3-7) The QRS11Pro gyro used on Rømer
Typical values for accuracy of ADCS sensors are shown in the
following table
Table 3-1 Ranges of ADCS sensors accuracy
Sensor Accuracy
Earth’s Horizon sensor
0.05 deg. (GEO)
0.1 deg. (LEO)
Sun sensor 0.01 deg.
Star mapper 2 arc. sec.
Magnetometers
1.0 deg. (5,000 Km altitude)
5.0 deg. (200 Km altitude)
Gyro 0.001 deg./hr

51. Chapter3 Attitude Determination
and Control Subsystem
32
3.4.2 ADCS Actuators
ADCS actuators are used to generate the required torque for correction
of satellite attitude. The generated torque is operated against the environmental
disturbance or to force the satellite to point to a cretin direction according to the
control system requirement. A brief description of the commonly used
actuators is presented in this section.
3.4.2.1 Momentum and Reaction Wheel
Momentum wheels and reaction wheels are similar in construction; they
are simply motor with a flywheel mounted on the motor shaft, the difference in
terminology resulting primarily from the speed at which they operate. A
momentum wheel typically operates at constant speed, providing a means of
momentum storage, which in turn provides gyroscopic stabilization to the
satellite. Reaction wheels generally operate at varying speed, providing means
of reacting torque. According to Newton's third law, as a torque is electrically
applied on the motor shaft to cause the wheel to accelerate, an equal and
opposite torque is generated on the satellite, causing the attitude to change.
Momentum wheels are commonly used singly or in pairs to provide spin
stabilization. Normally, reaction wheel system consists of four wheels. Three
reaction wheels are aligned to the satellite pitch, yaw and roll control axes. The
fourth wheel is skewed symmetrically with respect to the orthogonal control
axes. This commonly used configuration provides full redundancy for roll or
pitch or yaw in case of wheel failure. An image of typical reaction wheel is
shown in Figure (3-8)

52. Chapter3 Attitude Determination
and Control Subsystem
33
Figure (3-8) The TELDIX Momentum and Reaction
Momentum and reaction wheels have the advantage of providing quick
and accurate attitude control. Also, they can be used at any altitude. Their
disadvantage is that they can be costly, massive, and require large amounts of
power. However, wheels may saturate since the RW is a motor that has
maximum speed, since the angular momentum that can be stored in the wheels
is limited, so a secondary control system is used to prevent the stored
momentum from reaching the maximum limit. The secondary control system
can be thrusters system or magnetorquers. Momentum and reaction wheels are
used in Egyptsat1, FLTSATCOM, MAGSAT and SEASAT [15].
3.4.2.2 Magnetic actuators
Magnetic actuators enforce a torque on the satellite by generating a
dipole moment, which interacts with the Earth's magnetic field. Generally,
there are two types of magnetic actuators, torque coils and magnetic rods or
magnetorqure.
1. Torque Coils

53. Chapter3 Attitude Determination
and Control Subsystem
34
The torque coil is simply a long copper wire, winded up into a coil.
Generally, three coils are used, one coil in each axis as shown in Figure (3-9
The generated dipole moment L by each coil is calculated by
ANiL coil (3.1)
Where, coili is the current in the coil, N is the number of windings in
the coil, and A is the area spanned by the coil.
Figure (3-9) Torque Coils
2. Torque Rods
Torque rods operate on the same principle as torque coils, but instead of
a large area coil the windings is spun around a piece of ferromagnetic material
with very high permeability as shown in Figure (3-10). Ferromagnetic
materials, have a relative permeability, , of up to 106. the generated dipole
moment L is calculated by the following formula
ANiL coil (3.2)

54. Chapter3 Attitude Determination
and Control Subsystem
35
Hence, generating specified dipole moment from magnetic rod needs
current much lower than that needed to magnetic coil. However, the weight of
magnetic rod increases drastically because of the metal core in the rods.
Another inconvenience of the torque rods is the hysteresis effect associated
with ferromagnetic core which add nonlinearity to the control loop. Advantages
and disadvantages of using magnetic actuator will be discussed in details in
CHAPTER (5). Magnetic actuators are used with Egyptsat1, MAGSAT,
TIROS-IX, LANDSAT-D and AEROS-1, 2[15].
Figure (3-10) Torque rods
3.4.2.3 Thruster
Thruster works on the principle of Newton's third law, according to
which "for every action, there is an equal and opposite reaction". Referring to
this principle, if gas is propelled out of a nozzle, the satellite will accelerate in
opposite direction. However, if the nozzles are not pointed directly away from
the center of mass this will lead to cause rotational of satellite as well. In
addition, if two thrusters in opposite direction but not co-lined rotation only
will be generated. The source of the used gas defines the type of thruster .
Cold gass thrusters use high pressure storage tank. Hot gas thrusters use the
combustion of either monopropellant or bipropellant.
Six thrusters are needed to be mounted in pairs to generate the torque
needed for three-axis control. Thruster as actuator is highly accurate and

55. Chapter3 Attitude Determination
and Control Subsystem
36
generate higher torque than RW and magnetic rods. On the other hand, the
structure used with the thrusters is large and heavy. Besides, run out of either
gas or propellant will lead to stop functioning of thrusters. Thrusters are used in
ATS-3,6 , FLTSATCOM, GOES-I and SKYNET[15].
Figure (3-11) Torque generated thruster mounted to satellite
3.5 Disturbance Environment
In an Earth orbit, the space environment imposes several external
torques that the ADCS system must tolerate. According to orbit altitude, three
or four sources of disturbing torques are affecting the space craft[4]. These
torques are; gravity gradient, magnetic field effect, solar radiation pressure, and
aerodynamic forces. Those disturbances are affected by the satellite’s
geometry, orientation, and mass properties in addition to satellite orbital
altitude.
3.5.1 Gravity Gradient Disturbance
Any object with nonzero dimensions orbiting Earth will be subjected to
a “gravity-gradient” torque. In short, the portions of the satellite that are closer
to the Earth are subjected to a slightly larger force than those parts farther away
[7]. This creates a force imbalance that has a tendency to orient the satellite
towards the center of Earth in order to compensate this imbalance. According
to [15] the gravity gradient torque can be determined by equation (3.3) . The
worst case torque arises at
o
90

56. Chapter3 Attitude Determination
and Control Subsystem
37
)2sin(
2
3
3 iiZZgg JJ
R
T (3.3)
Where,
Tgg: is the resulting gravitational torque [Nm]
μ: is the gravitational constant of the earth [m³/s²] (μ = 3.896*1014
m³/s²)
Jii :is the moment of inertia tensor for the satellite in i axis.(in body
coordinate system) [kgm²] (i=x,y,z)
Is the maximum deviation angel from the local vertical [rad]
R: is the distance between satellite center of mass and earth center of
mass [km]
The previous formula for calculation of gravity gradient is used to give
course estimation of gravity gradient disturbance torque but an accurate
formula given in (4.28) is used in calculation of satellite mathematical model
3.5.2 Magnetic Field Disturbance
Magnetic field torques are generated by interactions between the
satellite magnetic dipole and the Earth’s magnetic field. This satellite magnetic
dipole is the summation of two components; first component is the induced
magnetic dipole, which is caused by current running through the satellite
wiring harness and second component is the residual dipole moment, which is
caused due to magnetic properties of the satellite components. The satellite
magnetic dipole exhibits transient and periodic fluctuations due to power
switching between different subsystems. These effects can be minimized by
proper placement of the wiring harness. The magnetic torque is calculated by
following formula
BDTm (3.4)
Where
D = the vector of total satellite magnetic dipole.
B = local geomagnetic field vector.

57. Chapter3 Attitude Determination
and Control Subsystem
38
In the worst case, the vectors are perpendicular to each other and the
cross product turns into a product of scalar values.
3.5.3 Solar Radiation Pressure Disturbance
Solar radiation pressure is a result of the transfer of momentum from
photons of light to the surface of the satellite. The result of this pressure across
the satellite surface is a force that acts through the center of pressure, psc , of the
satellite. In most cases, the center of pressure is not co-onside with the center of
mass of the satellite, thus a torque will be generated around the center of mass
cm see Figure (3-12). For Earth-orbiting satellite, where the distance from the
satellite to the Earth is small compared to the Earth-Sun distance, the mean
solar flux acting on the satellite is considered a constant (regardless of orbital
radius or position).
The solar radiation torque is calculated using the following equation [4] .
)()cos()1( gpssSp cciqA
c
So
T
(3.5)
Where
So is solar constant [W/m²] = 1428 W/m² (max)
c is speed of light [m/s] = 3*108
m/s
A is the cross sectional area subjected to solar radiation pressure [m²]
q is reflectance factor (0: perfectly absorbing, 1: perfectly reflecting)
si is the angle of sun light incidence [rad]
cps is the center of pressure [m]
cg is the center of gravity [m]
Referring to the previous assumptions, the solar pressure disturbance
torque is the only one that is not dependent of the orbit altitude. However, it is
dependent of the sun incidence angle i. The worst case torque arises at i = 0°.

58. C
3.5.
as
esp
torq
cha
to t
sign
effe
adT
Wh
is
cD i
A is
vc i
cps
cg i
3.6
com
Chapter3
.4 Aerod
Aerody
shown in
ecially at l
que is alm
anging of s
the aerodyn
nificantly
ects is calcu
Dc
2
1
here
s the densit
is the coeff
s the cross
s the orbita
is the cent
is the cente
Attitu
There
mpensation
dynamic D
ynamic torq
Figure (3
low altitud
ost negligi
ome param
namic drag
with solar
ulated by (
C cvA
2
ty [kg/m³]
ficient of d
sectional a
al velocity
ter of press
er of gravit
Fig
ude Contr
are differe
n and to ma
Disturbanc
ques are du
3-12. Aero
des (less th
ible. These
meters, such
g during ti
r activity.
(3.6) .
gpa cc
drag
area subjec
[m/s]
sure [m]
ty [m]
gure (3-12)
rol techniq
ent techniq
aintain the
39
ce
ue to atmo
odynamic
an 500). A
e torques i
h as cross
lting. In ad
The gene
cted to atm
Sunlight a
ques
ques to app
required or
A
a
ospheric dr
torques ca
At higher a
is difficult
sectional a
ddition, atm
erated torq
mospheric d
and drag ef
ply contro
rientation .
Attitude De
and Contro
rag acting o
an be qui
ltitudes the
to be calc
area of sate
mospheric
que due to
drag [m²]
ffect
ol torque fo
. For these
eterminatio
l Subsystem
on the sate
ite signific
e aerodyna
culate beca
ellite subje
density va
o aerodyna
(3.6)
for disturba
purposes,
on
m
ellite
cant,
amic
ause
cted
aries
amic
ance
two

59. Chapter3 Attitude Determination
and Control Subsystem
40
types of control techniques are often employed , passive and active control
[4][12]. Since Attitude control system, is highly mission dependent, so the
decision to use a passive or an active control technique or a combination of
them depends on mission pointing and stabilization requirements.
3.6.1 Passive Control
For missions with rather coarse orientation requirements, passive control
techniques are used for attitude control. The main advantageous of these
techniques are saving resources concerning both mass and power and the
associated cost. In addition, they provide longer lifetime for the space mission.
However, a poor pointing accuracy is obtained. The most common passive
control techniques are passive magnetic system (i.e. Permanent magnate),
gravity gradient and spin stabilization [4].
3.6.1.1 Passive magnetic
In this method, the concept of magnetic compass is applied, that is, the
satellite is equipped with permanent magnet that will keep the alignment
between certain axis of the satellite with geomagnetic field vector .As a result,
the south pole of the magnet will be drawn towards the magnetic north pole of
the Earth, and vice versa. This will lead to a slight tumbling motion with two
revolutions per orbit and no possibilities of controlling spin around the magnets
axis as shown in Figure (3-13) so continues nadir pointing will not be possible.
Permanent magnet technique is used in AZUR-1 [15].

60. Chapter3 Attitude Determination
and Control Subsystem
41
Figure (3-13) passive magnetic control orientation profile.
3.6.1.2 Gravity-gradient stability
Gravity-gradient stability uses the mass characteristics of the satellite to
maintain the nadir pointing towards Earth (as described in 3.5.1). The
magnitude of gravity-gradient torque decreases with the cube of the orbit
radius, and symmetric around the nadir vector, thus not influencing the yaw of
satellite. Therefore, the gravity gradient stability is used in simple satellite in
LEO without yaw orientation requirements [4].
Yet, stability in the gravity gradient case depends upon the the
configuration of the mass characteristics of the space craft. The following
condition is necessary for gravity-gradient stability [12]:
JzzJxxJyy&JzzJxxJyy (3.7)
Where Jii :is the moment of inertia tensor for the satellite in i axis.(in
body coordinate system) (i=x,y,z)

61. Chapter3 Attitude Determination
and Control Subsystem
42
As a result, the gravity gradient stability can be achieved by
manipulation of lay out of the satellite's components to grantee the above
mentioned condition (3.7). Other solution is to add a sufficient mass on a
deployed boom to reach the stability condition. This will increase the moment
of inertia in the directions transverse to the boom, and the satellite will be
stable with the mass pointed toward or away from the earth. Gravity gradient
stability is suffering from continuous oscillation about nadir due to lack of
damping. Hence, gravity-gradient stabilization should be supported with
damping system to reduce the small oscillation around the nadir vector.
Gravity-gradient stabilization technique is used in DODGE, GEOS-3, and
RAE-2 [15].
3.6.1.3 Spin stabilization
Spin stabilization technique applies the gyroscopic stability to passively
resist the effect of disturbance torques about the spinning axis. Spin-stabilized
satellites spins about their major or minor axes, so angular momentum vector
remains approximately fixed with respect to inertial space. [15]. Spinning
satellite is classified according to spinning object to single or dual spin. The
stability criteria and the corresponding spinning axis is predicted according to
the following analysis.
3.6.1.3.1. Single Spin
In single spin satellites, the whole satellite spins about the angular
momentum vector as shown in Figure (3-14) This method of stabilization is
simple and has a high reliability. The cost is generally low, and it has a long
system life. However, Spin-stabilized satellite are subject to nutation and
precession, but have a gyroscopic resistance which provides stability about the
transverse axis.
On the other side, spinning satellite will have poor maneuverability.
Beside, it will not be suitable for systems that need to be Earth pointing, such

62. Chapter3 Attitude Determination
and Control Subsystem
43
as payload scanners and communication antennas. Single spin stabilization
technique is used in AEROS-I,2, ALOUETIE-I,2and ARIEL-I [15].
Figure (3-14) spin stabilization
3.6.1.3.2. Dual Spin
In satellite with dual spin, a major portion of the satellite is spun, while
the payload section is despun. This technique is favorable because fixed inertial
orientation is possible on the despun portion. This method of stabilization has a
few disadvantages, however. This system is much more complex, which leads
to an increase in cost and a decrease in reliability. In addition, the stability is
sensitive to mass imbalances. Duel spin stabilization technique is used in ANS,
ATS-6, SEASAT and SMM [15].
3.6.2 Active control techniques
For complex mission requirements, satellite requires continues
autonomous control about the three axes during the mission. In general, active
control systems employ momentum exchange wheels, magnetic control
devices, and thrusters. Advantages of these systems are high pointing accuracy,
and a not constrained to inertial pointing like spin stabilization technique.

63. Chapter3 Attitude Determination
and Control Subsystem
44
However, the hardware is often expensive, and complicated, leading to a higher
weight and power consumption.
3.6.2.1 Momentum exchange Wheels
Three-axis stabilization through momentum exchange wheels applies
reaction wheels, momentum wheels, and control moment gyros. This is to
provide three axis stabilization. Advantages and disadvantages of this wheel
system are discussed in 3.4.2.1. Three-axis stabilization technique using wheels
is used in Egyptsat1, FLTSATCOM, MAGSAT and SEASAT [15].
3.6.2.2 Magnetic actuators
Magnetic actuators devices use the interaction of the satellite magnetic
dipole moment and the Earth’s magnetic field to provide a control torque.
Magnetic control torques work better in low Earth orbits than higher orbits,
such as geostationary, because as the distance from the Earth increases, the
geomagnetic strength decreases. Advantage and disadvantage of magnetic
actuators is discussed in 3.4.2.2 Three-axis stabilization technique using
magnetic actuators is used in Egyptsat1, MAGSAT, TIROS-IX, LANDSAT-D
and AEROS-1, 2[15].
3.6.2.3 Thrusters
Mass propulsive devices, such as thrusters, can be used for three-axis
stabilization. These often consist of six or more thrusters located on the satellite
body. The strength of the obtainable torque is dependent on the thrust level as
well as the torque-arm length about the axis of rotation. Advantage and
disadvantage of thrusters is discussed in 3.4.2.3 3.4.2.2. Three axis stabilization
technique using thrusters is used in ATS-3,6 , FLTSATCOM, GOES-I,
SKYNET[15].

64. Chapter 4 Control System Modeling
45
CHAPTER (4)
CONTROL SYSTEM MODELLING
4.1 Reference Coordinate Systems
Several different reference coordinate systems or reference frames are
used to describe the attitude of a satellite in orbit. The most utilized coordinate
systems employed in attitude control problem are the inertial, Greenwich,
orbital, body, and device frames.
4.1.1 Geocentric Inertial Coordinate System
The Geocentric Inertial Coordinate System or Earth-Centered Inertial
(ECI)coordinate system has its origin in the Earth center The IZ -axis points is
the axis of rotation of Earth. The IX -axis is in the direction of the vernal
equinox, and the IY -axis completes the right-hand rule for the coordinate
system. A demonstration for the geocentric inertial coordinate system is shown
in Figure (4-1).
4.1.2 Greenwich Coordinate System
The Greenwich Coordinate System or Earth-centered Earth-fixed
reference frame also has its origin at the center of the Earth, but it rotates
relative to inertial space, shown in Figure (4-2) The GZ -axis direction is the axis
of rotation of Earth. The GX -axis points to the Greenwich Meridian, and the GY
-axis completes the right-hand rule for the coordinate system

65. Chapter 4 Control System Modeling
46
Figure (4-1) Inertial coordinate system
Figure (4-2) Greenwich coordinate system

66. Chapter 4 Control System Modeling
47
4.1.3 Orbital Coordinate System
The orbital coordinate system (OCS) is located at the mass center of the
satellite. This frame is non inertial because of orbital acceleration and the
rotation of the frame.
The motion of the frame depends on the orbit altitude. The -axis in the
direction from the satellite to the Earth , OZ -axis in the direction opposite to
the orbit normal, and the OX -axis is perpendicular to the OZ -axis and OY -axes
according to the right-hand rule . In circular orbits, OX is the direction of the
satellite velocity. The three directions OX , , and are also known as the roll,
pitch, and yaw axes, respectively. Figure (4-3) shows a comparison of the
inertial and orbital frames in an equatorial orbit.
Figure (4-3) orbital coordinate system
4.1.4 Body Coordinate System
Like the OCS frame, the body coordinate system has its origin at the
satellite’s mass center. This coordinate system is fixed in the body. The -axis in
the direction from the satellite to the Earth , -axis in the direction opposite to
the orbit normal, and the -axis is perpendicular to the -axis and -axes
according to the right-hand rule . In circular orbits, is the direction of the

67. Chapter 4 Control System Modeling
48
satellite velocity. The relative orientation between the orbital and body frames
is the satellite attitude, when the satellite is nadir pointing OCS is co-onside
with BCS
Figure (4-4) Body coordinate system
4.1.5 Device Coordinate System
The device coordinate system is fixed at the device body (i.e. sensor or
actuator …). It define the orientation of the device with respect to satellite BCS
.As shown in Figure (4-5) the ZD- axis is Z-axis of the device 's body and XD-
axis is X-axis of the device 's body and YD-axis is perpendicular to ZD-axis and
XD-axis

68. Chapter 4 Control System Modeling
49
Figure (4-5) device coordinate system
4.2 Modeling of Satellite Rotation Around it's Center of Mass
In this section, derivation of the equations used for modeling the
kinematics and dynamics of satellite rotational motion. These equations are
borrowed of Bhanderi, 2001.
In general, kinematics equations involved in the satellite model are
represented through three types of parameters. The direction cosine matrix has
the disadvantage of having nine parameters to represent three degrees of
freedom motion. Due to this redundancy, numerous ways of representing the
satellite attitude with a minimum set of parameters have been developed.
Euler angles describe the rotation around the principal axes and use
therefore only three parameters. However some singularities arise for some
rotations, which is why Euler angles are commonly used when the attitude of
the object involved, is known to be within a certain margin to avoid this
singularities [Wertz, 1978].
Quaternions use four parameters with a single constraint, to represent
attitude, and are subjected to no singularities. This is useful when considering
that the attitude of a satellite is usually unknown after the release from the
launcher. For this reason quaternions are commonly used in space. Appendix A

69. Chapter 4 Control System Modeling
50
gives a brief description of the Euler angles, direct cosine matrices and
quaternions.
The modeling of a satellite’s rotational motion is divided into the
kinematic equation and the dynamic equation. The kinematic equation
describes the change in the attitude parameters of the satellite, regardless of the
forces acting on it. The dynamic equation describes the time dependent
parameters as functions of external forces.
4.2.1 Model of Dynamic Equation
Here we assume that satellite is a rigid body moving in ICS. Then
satellite motion can be described by the translation motion of its center of mass,
in addition to a rotational motion about some axis through its center of mass. In
the following analysis, depend on the well-known operator equation acting on a
given vector [13][14].
w
dt
d
dt
d
B (4.1)
Where
B vector defined in BCS
I vector defined in ICS
Figure (4-6) Angular motion of rigid body

70. Chapter 4 Control System Modeling
51
which simply states that "the rate of change of the vector A as observed
in the fixed coordinate system I (e.g. ICS) equals the rate of change of the
vector A as observed in a rotating coordinate system B (e.g. BCS) with angular
velocity w , plus the vector product Aw ". In Figure (4-6), it is assumed that,
an orthogonal three axis frame has its origin O located at the center of mass of
the satellite body B ; i, j, k are the respective unit vectors along BCS. So for
any particle im , in the satellite body B, rRR , hence
iioiioi rwvvrwrRR (4.2)
Where
w is the angular velocity vector of the body B with respect to ICS.
The angular momentum H of a body particle im , using (4.2) can be
expressed as
)( iioiiiiii rwrRmrRmrH (4.3)
However, by definition we have 0ii vr in a rigid body, so in this case
it follows that
)()( iiiiioioiii rwmrrmvrwvmrH (4.4)
To find the angular momentum of the entire body, we shall sum the
momentum components of all the mass particles
i i
iiiiio rwmrrmvH )(
(4.5)
Since the angular motion is about the center of mass
i
iirm 0 so (4.5) can be
rewritten as

71. Chapter 4 Control System Modeling
52
i
i
ii mrwrH )(
(4.6)
After performing the vector triple product, we get the following equations
i i
iiiyiiix
i
iiiz
i i
iiiziiix
i
iiiy
i i
iiiziiiy
i
iiix
mzywmzxwmxywk
mzywmyxwmzxwj
mzxwmyxwmzywiH
)(
)(
)(
22
22
22
(4.7)
Where iii zyx ,, are the coordinates of a particle i in the BCS and
zyx www ,, are the angular velocity comportments around kji ,, body axes. The
summations of the squared coordinate components are easily identified as the
three moments of inertia of the body about its three orthogonal axes. The
summations of the products of the coordinate components are identified as the
products of inertia. With these definitions equation (4.7) can be rewritten as
zyyzxxzzzyzzyxxyyyxzzxyyxxx JwJwJwkJwJwJwjJwJwJwiH
(4.8)
zyx kHjHiHH
(4.9)
If we define the angular velocity vector which describe the angular
velocity of BCS with respect to ICS as T
zyx ][ then (4.9) can be rewritten
as
I
JJJ
JJJ
JJJ
H
z
y
x
zzyzxz
yzyyxy
xzxyxx
(4.10)

72. Chapter 4 Control System Modeling
53
Where J the inertia tensor or inertia matrix
The dynamic equation of motion can be derived through applying
Newton’s second law for rotational motion, where the rate of change in angular
momentum of the satellite is equal to the sum of all external torques. and
recalling (4.6)
ii
k
i
i
k
i
i
vmr
HH
1
1
(4.11)
Where ir is the position of the i th
particle with mass im and velocity iv .
Taking the time derivative of Equation (4.11), yields
k
i
iiiiii amrvmvH ).( (4.12)
ia is the acceleration of the i th
particle. The first term under the
summation of Equation (4.12) is a cross product of two parallel vectors, which
is zero. Realizing that iami is the force acting on the i th
particle yields
extTH (4.13)
Where extT is the sum of external torques acting on the satellite. Such as
controlling torques cT , gravity gradient ggT and other external disturbance disT
(i.e. aero drag, magnetic disturbance….)
cdisggext TTTT (4.14)
Equation (4.13) holds only, if the internal torques sum up to zero (i.e.
the body is rigid)[10]. An expression of the derivative of the angular
momentum in terms of the satellite’s angular velocity is sought, in order to
obtain the dynamic equation.

73. Chapter 4 Control System Modeling
54
In ICS frame, denoted I , the angular momentum of the satellite can be
expressed as a function of the angular velocity and the moment of inertia
matrix J of the satellite, by
II
JH (4.15)
Since the moment of inertia is more conveniently expressed in the BCS
frame, denoted B , the angular momentum is found in the body frame. The
transformation matrix B
IA represents the rotation from the inertial frame to the
satellite body frame, which is used to represent Equation (4.15) in the body
frame, yielding
IB
I
B
HAH (4.16)
The derivative of
B
H is given by
IB
I
IB
I
IB
I
B
HAHA
HA
t
H
(4.17)
In order to obtain an expression for B
IA consider the kinematic equation
for rotating systems, which for the angular momentum vector H is
BBIB
BBBI
HHH
HHH
(4.18)
Since IB
I
BI
HAH , combining Equations (4.17) and (4.18), gives
IB
I
BIB
I
HA
HHA
(4.19)
Defining the cross product matrix function as
0
0
0
)(
12
13
23
vv
vv
vv
vS (4.20)
Where vis an arbitrary vector, Equation (4.19) is written

74. Chapter 4 Control System Modeling
55
IB
I
IB
I HASHA (4.21)
Since Equation (4.21) holds for all the sought expression for the
derivative of the attitude matrix is
B
I
B
I ASA (4.22)
Inserting Equation (4.22) into Equation (4.17), gives
IB
I
IB
I
B
HAHASH (4.23)
Recalling from Equation (4.13), that the derivative of the angular
momentum is the external torques and applying the attitude matrix rotations in
Equation (4.23), yields
B
ext
BB
THSH (4.24)
Finally the angular momentum is expressed in terms of the moment of
inertia and the angular velocity, as given in Equation (4.15). Solving with
respect to gives the sought nonlinear differential equation, written in the
form
JTJ
B
ext
1
(4.25)
Where the superscript of frame is left out, since all vectors and matrices
are given in the BCS frame.
If the satellite is equipped with reaction wheels, the total angular
momentum is given by
wHJH (4.26)
Where wH is the angular momentum of the wheels.
Using Equation (4.26) and (4.14)in the derivation of the dynamics
above, yields
wwcdisgg HHJTTTJ 1
(4.27)
Where wH is the sum of the internal torques, generated by the
momentum wheels.

75. Chapter 4 Control System Modeling
56
Gravity gradient model
According to [15] the gravity gradient torque is given as
Jerer
R
T
cm
gg 3
3
(4.28)
Where is the Earth gravitational constant, cmR is the distance from the
centre of the Earth to the satellite’s centre of gravity ( cmR is a subject of
variation, when an elliptic orbit is considered), er is the zenith. Observe that
the zenith is equivalent to is the third column in the rotation matrix from OCS
to BCS and the constant
2
3
3
O
cmR
, where O is the orbit rate.
2
3
2
2
2
1
2
0
1032
2031
2
2
er (4.29)
Where the general form of quaternion is represented in appendix A.3
By substituting the gravity gradient torque defined by equation (4.28)in
(4.27) then the full dynamic model of satellite is introduced as follows
cdisoww TTerJerHHJJ )(3 21
(4.30)
If the satellite is controlled without wheels then the dynamic model of
satellite will be
cdiso TTerJerJJ )(3 21
(4.31)

76. Chapter 4 Control System Modeling
57
4.2.2 Model of Kinematic Equation
Let the attitude of a satellite at time t and tt be denoted )(t and
)( tt . If the rotation of the satellite in the time period t is denoted )( t the
propagation of the attitude from t to tt can be written
)()()( tttt (4.32)
Writing )( t in terms of rotation angle around the vector u in time
t yields.
)
2
sin(
)
2
sin(
)
2
sin(
)
2
cos(
)(
3
2
1
u
u
u
t (4.33)
Assuming that u and are constant over the time t and using the
definition of the quaternion product equation (3.3) is written
)
2
sin(
)
2
sin(
)
2
sin(
)
2
cos(
)()(
3
2
1
u
u
u
ttt (4.34)
Where 44I is the 4 by 4 identity matrix. For infinitesimal small time
steps can be approximated by
ty (4.35)
Where y is the instantaneous angular velocity of the satellite. Using
small angle approximations, Equation (4.34) can be expressed as

77. Chapter 4 Control System Modeling
58
y
t
u
y
t
u
y
t
u
ttt
2
2
2
1
)()(
3
2
1
(4.36)
Realizing that yu Equation (4.36) can be rewritten
y
t
y
t
y
t
t
y
t
y
t
y
ttt T
22
.
2
2
2
2
1
)()( 00
3
2
1
(4.37)
The differential equation of )(t is defined as
t
ttt
t
)()(
lim0
(4.38)
Inserting Equation (4.36) yields the sought kinematic differential equation
2
1
).(
2
1
0 yyyT
(4.39)
Where Y is the instantaneous angular velocity of the satellite in quaternion
form and 3,2,1& iyi is the components of angular velocity vector.
3
2
1
0
y
y
y
(4.40)
The above kinematics differential equation is represented using relative
angular velocity between satellite and orbital frame y . However, the dynamic
model of satellite is calculated using absolute angular velocity of satellite , so
it is more convenient to introduce the satellite kinematics through absolute

78. Chapter 4 Control System Modeling
59
angular velocity. Since the satellite angular velocity with respect to ICS, is sum
of the orbital angular velocity O measured in BCS and satellite relative angular
velocity[16]
yeno (4.41)
0132
2
3
2
2
2
1
2
0
0321
2
2
en (4.42)
Where en is the 2nd
column in the rotation matrix from OCS to BCS see
(A-17) .To get the kinematics differential in terms of absolute angular velocity,
substitute in (4.39) in terms of from equation (4.31) and make algebraic
arrangements
0
0
00
2
3
2
1
o
(4.43)
4.2.3 Linearized Equations of Motion
In this section, the equations of motion are linearized in terms of
quaternion to be fitted in the slandered stat space representation.
FUAXX (4.44)
Where
AIs the system matrix of linearized equations.
F Is the input matrix for control.
U Is the vector of input control torque.
The input control torque applied to this system is generated by
magnetorqure in form of interaction beteen the Earth magnetic field B and the
magentourquer dipole moment L . To obtain the input torque from the
magnetorquer, The required magnetic dipole moment is calculated as [12].

79. Chapter 4 Control System Modeling
60
2
B
UB
L
(4.45)
Where B is Earth magnetic field measured in BCS
L is the required dipole moment generated by magnetorqure
U is the required control torque.
The generated torque genT due to the interaction between Earth
magnetic field B and magnetorqure dipole moment L is given by
The state vector X contains the vector portion of the quaternions and
their rates of change
3
2
1
3
2
1
y
y
y
X (4.47)
Since, for three-axis stability, the body frame should be aligned with the
orbital frame, or
0
0
o
(4.48)
0
10
(4.49)
This relation implies that the satellite nadir vector always points to the
center of the Earth. Therefore, using equations (4.49) and Error! Reference
2
B
UBB
LBTgen
(4.46)

80. Chapter 4 Control System Modeling
61
source not found. the linearized rotation matrix from OCS to the BCS could
be easily calculated by substituting 1,0.&. 00 iiii where 3,2,1i .
122
212
221
)(
12
13
23
R (4.50)
And therefore er and en will be
1
3
1
2
2
1
2
&
1
2
2
ener (4.51)
The angular rotation rate o of the orbital frame with respect to the ICS
measured in BCS ow is
1
3
2
2
o
o
o
oo enw (4.52)
Let’s note, the vectors enand ermeet Poisson’s equations [16]
Recalling the relation (4.41).
owy (4.54)
y can be expressed as
1
3
2
0
2
o
o
y (4.55)
In addition recalling equation (4.39), therefore, satellite relative angular
velocity y can be expressed as
)(2
2
00
y
(4.56)
Assuming small angles, 3,2,1,0&0&1 00 iii .Therefore
2y (4.57)
Substituting (4.57)in (4.54)
0&0 enyneeryre (4.53)

81. Chapter 4 Control System Modeling
62
The A matrix can be calculated by beginning with the change in
angular velocity measured in the body frame using satellite equation of motion
through substitution, the first portion of (4.31) is determined to be
Substituting from equation (4.58) in (4.59) assuming
3,2,1,0&0 iiiii
Similarly, the gravity gradient torque is calculated as
Substituting Equations (4.61),(4.60) and (4.48), into (4.31) provides the
following relation
o
o
o
y
y
y
2
2
3
2
31
(4.58)
21
3
12
31
2
31
32
1
23
1
.
.
.
J
JJ
J
JJ
J
JJ
JJ (4.59)
3
2
1
3
12
1
2
3
1
23
1
2
0
2
oo
oo
y
J
JJ
y
J
JJ
JJ (4.60)
0
2
2
33 2
2
31
1
1
23
22
J
JJ
J
JJ
erJer oo (4.61)

82. Chapter 4 Control System Modeling
63
Where
Where
It is important to keep in mind that the values of 1 , 2 and 3 are limited
and that they are smaller than unity [12].Referring to stat space system given
in (4.44),satellite dynamics model given in (4.31) and the magnetic torque
equation (4.47) , The input matrix F is calculated as
Where 3,2,1,iBi are the components of measured Earth magnetic field.
FL
y
y
y
A
y
y
y
3
2
1
3
2
1
3
2
1
3
2
1
(4.62)
00)1(200
000060
)1(00008
2
1
00000
0
2
1
0000
00
2
1
000
3
2
3
2
2
1
2
1
oo
o
oo
A (4.63)
3
12
3
2
31
2
1
32
1 &&
J
JJ
J
JJ
J
JJ
(4.64)
2
2
2
13231
32
2
3
2
121
3121
2
3
2
2
2
1
2
1
2
1
)(
)(
BBBBBB
BBBBBB
BBBBBB
B
J
BB
B
J
F
FUUBB
B
J
Tc
(4.65)

83. Chapter 4 Control System Modeling
64
4.2.4 Gravity Gradient Stability
Having established the equations of motion of the rigid body in space
and a torque acting on the satellite as a function of its attitude and mass
properties. The following analysis will demonstrate the conditions under which
the satellite is naturally stable.
Recalling y2 , (4.57) , (4.63) and (4.64) therefore the linearized
homogeneous equations of motion subject to gravity gradient is given as.
Stability about the Y-Body Axis
By taking Laplace -Transformation of (4.67), the characteristic equation
for the motion about the y-axis becomes
By simple inspection , (4.69) is a second order system , with no
damping term, i.e. the pitch motion is a simple harmonic oscillator as long as
So if 31 JJ ,the satellite is pitch stable with a frequency given in
(4.71) and an amplitude equal to the initial pitch condition ; if not, the pitch
equation is unstable and the satellite will swing away from the equilibrium
condition when disturbed
Stability about the X and Z-Body Axis
0)1(4 311
2
11 oo (4.66)
03 2
2
22 o (4.67)
0)1( 133
2
33 oo (4.68)
03 2
2
2
2
os (4.69)
31 JJ (4.70)
23opf (4.71)

84. Chapter 4 Control System Modeling
65
By taking Laplace -Transformation of (4.66) (4.68), the characteristic equation
for the motion about the x-axis and z-axis becomes
The roots of the above characteristic equation is
If 1s is a root of equation (4.72) , then for 1s to be root with non-positive
real part the following three conditions must be fulfilled[12].
since 1 , 2 and 3 are limited and that they are smaller than unity [12]
then the fowling relation are valid
From (4.75) it follows that
Figure (4-7)shows the regions of stability in the 31 plane resulting
from conditions (4.74) and (4.70). The four quadrants are labeled I, II, III and
IV. Quadrants II and IV are immediately instable, due to violation of condition
2nd term in (4.74) . Quadrants I and III are equally divided by a line, for which
21 ; only systems with 31 (below the dividing line) are stable. The
curve in quadrant III shows the solution to inequality in 1st term of (4.74), with
unstable systems being located below the curve. This leaves only two stable
regions, labeled A and B. for sub-region A that 312 JJJ in addition to (4.76),
for region B it follows that 321 JJJ in addition to 321 JJJ . Beletsky
derived these conditions in 1959 [17].
0431 31
2
311
24
oo ss (4.72)
2
163131 31
2
311311
2
2
o
s
(4.73)
031
0
431
311
31
31311
(4.74)
1&1&1
3
12
3
2
31
2
1
32
1
J
JJ
J
JJ
J
JJ
(4.75)
312 JJJ (4.76)

85. Chapter 4 Control System Modeling
66
Figure (4-7) plane showing regions of stability and instability; adapted
from[12]
4.3 Satellite center of mass motion model
Satellite motion can be considered a motion of the satellite under the
central force held of the Earth and the disturbed motion caused by other
perturbation forces. Therefore, the Keplerian orbits are important in orbit
theory and will be discussed in this section
4.3.1 Satellite orbits and Keplerian elements
The physical laws describing the motion of planets and satellites was
first described by Johann Kepler [1571-1630] and is mathematically derived
from Newton’s equations of motion for instance in Forssell (1991). Kepler’s
three laws state that:
1. The orbit of each planet is an ellipse, with the Sun at one of the foci
2. The line joining the planet to the Sun sweeps out equal areas in equal
times.
31

86. Chapter 4 Control System Modeling
67
3. The square of the period of a planet is proportional to the cube of its
mean distance from the Sun
These laws are also applicable to satellites orbiting the Earth, with one
modification. The orbit is not limited to an ellipse, but can be any conical
section. The laws of Kepler are valid under the assumption that the satellite and
the Earth are point masses, and that gravitational forces are the only forces
acting on the two bodies. It is also assumed that the two masses are not under
influence of gravitational forces from other celestial bodies than each other.
The satellite’s orbit will, as it is not leaving the Earth, be an ellipse with the
center of the Earth at one of the foci.
The mathematical background for Kepler’s laws comes from Newton’s
laws. To establish the dynamics of a satellite’s orbit position, it is useful to look
into Newton's gravitational studies. The law of universal gravitation states that
the force, f , acting on the satellite with mass, m , due to the Earth’s mass, Me ,
is
,2
r
r
r
mMeG
f
(4.77)
Where r is the vector from the center of the Earth to the satellite, and G
is the universal gravitational constant. With no other forces than gravity,
Newton’s second law
rmamf (4.78)
Where G is the universal gravitational constant, Meis the mass of the
Earth; r is the distance between the mass centre of the- Earth and the mass
centre of the satellite. The equation of satellite motion is then
,2
r
r
r
r
(4.79)
Where )( GM is called Earth's gravitational constant, and r modules
of the vector r .
Taken into account that the Earth gravitation force is always directed to
the Earth center and its absolute value ga is defined using Newton’s formula

87. Chapter 4 Control System Modeling
68
2
r
ag
(4.80)
When r is defined in GCS , gr , so Equation (4.79) can be written in
GCS as
gz
gy
gx
g
g
gg
a
a
a
r
r
ar
(4.81)
Since it is convenient to calculate the satellite position and poison rate
relatively to the Earth (i.e. in GCS), this can be done as follows using (4.1) and
making necessary algebraic reduction
)( gg r
dt
d
v (4.82)
e
ew
rewewvewr
r
dt
d
v
ggg
gg
0
0
2
)(
(4.83)
Where
gz
gy
gx
g
r
r
r
r is vector repressing the satellite position defined in GCS
gz
gy
gx
g
v
v
v
v is vector repressing the satellite liner velocity defined in GCS
e is the Earth rotation velocity
So finally the differential equation describing the satellite center of mass
motion in orbit will be:

88. Chapter 4 Control System Modeling
69
gzgz
gygy
gxgx
gzgz
gxgygygy
gygxgxgx
vr
vr
vr
av
vereav
vereav
2
2
2
2
(4.84)
Where gv and gr are the velocity vector and position vector in GCS

89. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
70
CHAPTER (5)
ANALYSIS OF CONVENTIONAL CONTROLLERS AND
DEVELOPMENT OF A NEW COMBINED
CONTROLLER
The purpose of this chapter is to present, discuss and compare between
commonly used attitude control algorithms for satellite actuated with magnetic
actuators only. Performances are demonstrated with simulations.
Since the ADCS tasks as mentioned before in 3.2 is to control the
angular motion of satellite starting from separation from launcher then attitude
acquisition and then keep satellite stabilization at nadir pointing Figure (5-1)
shows the ADCS functional diagram according to this functional diagram
ADCS magnetic control algorithms is divide to angular suppression algorithms,
in addition to attitude acquisition and stabilization algorithms[18],[19] in all
previous works attitude acquisition and stabilization are considered similar and
the same control law is used in both [20],[21].
5.1 Attitude Magnetic control concept
The main concept of magnetic attitude control of satellite is to generate
dipole moment L . Which is reacting with the earth magnetic filed B generating
torque cT used to orient the satellite.
BLTC (5.1)

90. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
71
Above general magnetic torque equation, conclude that the magnetic
torque acts in a direction orthogonal to both the magnetic field and the dipole
moment see Figure (5-2)
Figure (5-1) ADCS functional diagram

91. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
72
Figure (5-2) Magnetic Torque Direction
often, the desired direction of torque is not perpendicular to the magnetic
field. In this case, only the component of the desired torque in the direction
perpendicular to the magnetic field is possible and can be developed. This
relationship is demonstrated graphically in where dT is the desired torque , or
ideal, torque, , genT is an generated magnetic torque and is the undesired
component of torque, as described in [22]see Figure (5-3)
The moment developed in MT is determined by attempting to minimize
the magnitude of the undesired magnetic torque, T , such that
gend TT minimum (5.2)
This leads to [12]
2
B
TB
L d
(5.3)

92. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
73
Figure (5-3) Magnetic Control Torques[23]
5.2 Controllability
The satellite actuated by a set of magnetorquers has a serious
limitation[26]. The mechanical torque, produced by the interaction of the
geomagnetic field and the magnetic field generated by the magnetorquers, is
always perpendicular to the geomagnetic field vector. Thus, the direction
parallel to the geomagnetic field vector is not controllable. The geomagnetic
field changes its orientation in the OCS when the satellite moves in orbit. This
implies that e.g. yaw is not controllable over the poles but controllable over the
equator, see Figure (5-4)
Therefore beside the magnetic control it is required another source of
torque to control the satellite, when it is magnetically uncontrollable. This
source of torque can be expensively achieved by so-called momentum bias
configuration [12],[15] or cheaply achieved by using gravity gradient

93. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
74
torque[18]. Our study will focus in using gravity gradient torque beside the
magnetic torque to control the satellite
Figure (5-4)Control torque is always perpendicular to the geomagnetic field
vector.
This implies that yaw is not controllable over poles, and roll is not controllable
over equator.
5.3 Angular Velocity Suppression
The objective of the angular velocity suppression or detumbling
controller is to suppress the high angular velocity of satellite obtained due to
separation from launcher. Commonly there are two methods used for satellite
angular suppression, angular velocity feed back and B-dot technique

94. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
75
5.3.1 Angular suppression using velocity feed back
The main idea here is to use controller able to dissipate the satellite high
energy gained during separation from launcher. A very simple controller is
suggested in [20] which use angular velocity measurements from gyro, the
functional block diagram for velocity feedback controller is shown in Figure
(5-5 ). The stability of velocity feedback is examined below using the energy
consideration
Figure (5-5) Function diagram of velocity suppression using velocity feed
back algorithm
5.3.1.1 Energy Considerations
The total energy of the satellite is divided into kinetic and potential
energy. Kinetic energy is principally a result of the rotation in the inertial and
Required
Dipole
Moment
ADCS Processor
MTz
MTy
MTx MM
Gyro
Control
Algorithms
B
B
Satellite

95. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
76
orbit frame. The sources for the potential energy are the gravity gradient and
gyro effects due to revolution about the Earth [18].
Kinetic Energy
The standard kinetic energy of the satellite is a quadratic form relating
the satellite absolute angular velocity with respect to ICS. In this study we
focus only on the rotation of the satellite w.r.t the reference coordinate system,
i.e. the OCS.
The total angular velocity of the satellite relative to ICS is a sum of the
satellite angular velocity w.r.t. the OCS, y and the angular velocity of the
satellite’s revolution about the Earth (i.e. the orbital rate), o . It is assumed that
the orbit is circular and thus the orbital rate, is constant, therefore the portion
due to the orbital rate is disregarded, then kinetic energy of the angular motion
is expressed as
yJyE T
Kin
2
1
(5.4)
Potential energy
The potential energy due to the gravity gradient is minimum (Egg = 0)
when the z- axis of BCS (the axis of minimum moment of inertia) is ideally
aligned with the z-axis of OCS, since there is no gravity gradient acting on the
satellite. Its maximum value is reached when the satellite attitude is such that
the z-axis of BCS coincides with the y-axis of OCS. The potential energy
associated with the gravity gradient can be then considered as a measure of the
inclination angle between z-axes of OCS and BCS. It is formulated as,
)(
2
3 2
zz
T
ogg JerJerE (5.5)

96. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
77
Where the vector er - as it was defined in (4.29) - is a unit vector
describes the orientation between z-axes of OCS and BCS .The moment of
inertia about the z- xis, zzJ , is subtracted from the right hand side of Eq.
(5.5)[20] to make the minimum energy equal to zero.
The potential energy has also a component originating from the
revolution of the satellite about the Earth. Consider the summand J in the
equation of dynamics(4.31) . Using (4.41) this term can be rewritten as
enJenenJyyJenyJyJ ooo
2
(5.6)
Where the vector en - as it was defined in (4.42) is a unit vector
describes the orientation between y-axes of OCS and BCS. Since enJeno
2
is
not dependent on the satellite's angular velocity, and hence gives a contribution
only to the potential energy. therefore, the potential energy due to the
revolution of the satellite about the Earth is
)(
2
1 2
enJenJE T
yyogyro (5.7)
The minimum of this energy (Egyro = 0) is obtained when the y axis of
BCS is aligned with the y axis of OCS, and maximum when the z axis of BCS
coincides with the y axis of OCS. The moment of inertia about the y- axis, yyJ ,
is added to the right hand side of (5.7) to make the minimum energy equal to
zero.The total energy can be expressed as
gyroggkintot EEEE (5.8)
Therefore, the complete form of the total energy is,
)(
2
1
)(
2
3
2
1 22
enJenJJerJeryJyE T
yyozz
T
o
T
tot (5.9)
5.3.1.2 Lyapunov Stability
Consider a Lyapunov candidate function expressing the total energy of
the satellite.

97. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
78
)(
2
1
)(
2
3
2
1 22
enJenJJerJeryJy
EV
T
yyozz
T
o
T
tot
(5.10)
This candidate function satisfies
00)(
0)0(
xxV
V
(5.11)
And has the equilibrium for )0(V
}
0
1
0
,
1
0
0
,
0
0
0
:),,{( ereny (5.12)
The time derivate of V equals the time derivative of satellite total energy
totEV (5.13)
Since me derivative of satellite total energy totE is
neJenreJeryJyE T
o
T
o
T
tot
22
3 (5.14)
Let’s note, the vectors en and er meet Poisson’s equations
0&0 enyneeryre (5.15)
Recalling the satellite dynamic equation (3.21) considering only gravity
gradient
co TJererSJSJ )(3
2
(5.16)
Where
0
0
0
12
13
23
3
2
1
xx
xx
xx
x
x
x
S (5.17)
Inserting the relation yeno into the satellite dynamics yields
)()()(3 2
enyJenySneJTJererSyJ oooco (5.18)
Using (5.18) into (5.14) yields

98. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
79
neJenreJer
yJenySneJTJererSyE
T
o
T
o
oooco
T
tot
22
2
3
()()(3(
(5.19
)
Using that 0)()( ySyT
and (5.15) we get
yenSJenyerSJer
enyJenyS
yenJSTJererSyE
T
o
T
o
oo
oco
T
tot
).().(3
))()(
).(.)(3(
22
2
(5.20)
This reduced to the simple expression
c
T
tot TyE (5.21)
Finally, we have
c
T
tot TyEV (5.22)
So if the controlling torque is chosen as angular velocity feedback as
shown below in (5.23)
yKT vC . (5.23)
Where
vK is the positive constant
Then,
yKyV v
T
.. (5.24)
Therefore, the satellite energy will dissipate, and the controller (5.23)
guarantees damming of the relative angular velocity to zero. Hence the
required dipole moment to generate the control torque (5.23) can be calculated
using (5.25)[12]
2
B
TB
L c
(5.25)
Where
L is the dipole moment
B is the earth magnetic filled

99. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
80
5.3.2 Angular suppression using B-dot technique
The main idea for the B-dot technique based on the fact that the
variation of earth magnetic field is slow (i.e. 3.34e-4 Hz), so the difference
between to successive measurements from magnetometer depends on the
rotation of satellite around it center of mass rather than the center of mass
motion in orbit. Commonly there are three methods used to express the
magnetic filed derivative.
Since the condition (5.22) required to guarantee satellite energy
dissipation could be rewritten in another form as follows
0c
T
Ty (5.26)
Since the generated torque, Tc due to earth magnetic filed, B and MT
dipole moment, L is given by
BLTC (5.27)
So the condition(5.26) will be
0)( BLyT
(5.28)
With the general rules for cross product manipulation
abba
baccba )()(
(5.29)
Condition(5.28) can be rewritten as
0)( ByLT
(5.30)
This inequality dictates that the magnetic moment L needs to have a
component, which is anti-parallel to the direction of y B. Maximum
efficiency, is provided by ensuring that the entire vector is anti-parallel. In
other words, the inequality can be solved by expanding (5.30) with a positive
scalar gain K
)( ByKL (5.31)

100. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
81
Since derivative of earth magnetic filed in BCS as given [28]
ByB (5.32)
Finally becomes the B-dot detumbling control law
BKL (5.33)
Therefore, the dipole moment calculated by the form (5.31) guarantees
satellite dissipation.
5.3.2.1 Angular suppression using B-dot technique No.1
Since the derivative of earth magnetic field B can be calculated using
magnetometer measurements and satellite relative angular velocity using
(5.32). However, the relative angular velocity y is calculated using (4.41) from
gyro measurements and orbital rat o by the following form
eny o (5.34)
Since the orbital rate is very small compared with satellite angular
velocity during detumbling mode and it can be neglected so equation (5.31)
can be rewritten as
)( BKL (5.35)
The block diagram for Angular suppression using B-dot technique No.1
is shown in Figure (5-6.)

101. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
82
BB
BKL
Figure (5-6 ) Block diagram of velocity suppression using B-dot technique No1
5.3.2.2 Angular suppression using B-dot technique No2
Here a simple way used to calculate the derivative of earth magnetic
field B done by a simple backwards difference method (i.e. calculation of the
difference between two successive magnetometer measurement
)(),( dTtBtB divided by the difference between the times measurements dT
) [23].
dT
tBdTtB
B
)()(
(5.36)
Then the required dipole moment is calculated from (5.33), The block
diagram for Angular suppression using B-dot technique No.2 is shown in
Figure (5-7)

102. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
83
dT
kBkB
B
)1()(
BKL
Figure (5-7 )Block diagram of velocity suppression using B-dot technique No2
5.3.2.3 Angular suppression using B-dot technique No3
This technique was developed by M Guelman and used in the Israeli
Guerwin-Techsat This satellite was a 50kg cube, launched in July 1998, and
successfully functioned for over 4.5 years. [23] the derivative of the magnetic
filed is calculated as
dT
tBdTtB
B
tBtBtB o
)()(
)()()(
(5.37)

103. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
84
Where
oB is the earth magnetic field in OCS
The block diagram for Angular suppression using B-dot technique No.3
is shown in Figure (5-13)
BKL
dT
tBdTtB
B
tBtBtB o
)()(
)()()(
Figure (5-8) Bock diagram of velocity suppression using B-dot technique No3

104. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
85
5.3.3 Simulation verification
The following data are used for verification of the above mentioned
angular velocity suppression controllers
Table 5-1initial data used for satellite simulation
Parameter Value
Satellite moment of inertia tensor
[kgm2
]
406.008.0
06.0805.0
08.005.06
Initial satellite angular velocity
[deg/s]
T
5.45.45.4
Maximum dipole moment
generated from MT [Am2
]
10
orbit altitude [Km] 660
Orbit eccentricity 0
Orbit inclination [deg.] 98
Orbit argument of perige [deg.] 0
Local time of ascending node 10:00 am
True anomaly[deg.] 0
Satellite residual dipole moment
Am2
T
2.03.05.0
Calculation of the desired final angular velocity
As it is shown in (5.24) the angular velocity feedback guarantees the
convergence of satellite angular velocity to zero. In other hand, because the
results of angular velocity feedback algorithm will be compared with those
using B-dot technique. Taking into consideration that the minimum angular
velocity using B-dot technique is achieved when the satellite follows the
magnetic filed (i.e. behave like a compass). Since, the magnetic filed rotates
two times pre orbital period (i.e. 6000 s for 660 km orbit altitude), therefore the
min angular velocity reached by B-dot technique is calculated as flows
sy o
o
d /12.0
3000
360
(5.38)

105. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
86
The following flow chart shows the cyclogram of angular velocity
suppression algorithm
Figure (5-9) Cyclogram of angular velocity suppression algorithm

106. Ch
5.3.
Figu
F
Fig
hapter 5
.3.1 Simu
Simula
ure (5-11)
Figure (5-1
ure (5-11)
lations res
ations resul
and it show
10) Satellite
satellite en
Analy
Devel
sults for an
lts for the c
ws that the
e angular v
nergy durin
ysis of
lopment of
87
ngular vel
controller (
e satellite a
velocity sup
feedback
ng angular
feedback
Conventio
f a New Co
locity feed
(5.23) are s
angular velo
ppression u
suppressio
onal Con
ombined Co
dback
shown in F
ocity reach
using angu
on using an
ntrollers a
ontroller
Figure (5-1
hed dy .
ular velocit
ngular velo
and
0 to
ty
ocity

107. Ch
Fig
5.3.
law
(5-1
hapter 5
gure (5-12)
.3.2 Simu
The da
ws (5.35)-(5
11) and it s
) required d
u
lation resu
ata presen
5.37) and
shows that
Analy
Devel
dipole mom
using angu
ults for B-
ted in Tab
simulation
the satellit
ysis of
lopment of
88
ment to sup
ular velocit
-dot techni
ble 5-1 use
ns results
te angular v
Conventio
f a New Co
ppress the s
ty feedback
iques
ed for veri
shown in
velocity re
onal Con
ombined Co
satellite an
k
ification o
Figure (5-
eached dy .
ntrollers a
ontroller
ngular veloc
f used con
-10) to Fig
and
city
ntrol
gure

108. Chhapter 5
Figure (5-
Analy
Devel
13) Satelli
(a)using B
(b)using B
(c)using B
ysis of
lopment of
89
ite angular
B-dot techn
B-dot techn
B-dot techn
Conventio
f a New Co
r velocity su
nique No. 1
nique No. 3
nique No. 2
onal Con
ombined Co
uppression
3
2
ntrollers a
ontroller
n
and

109. Chhapter 5
Figuree (5-14) sat
(a)u
(b)u
(c)u
Analy
Devel
tellite ener
using B-do
using B-do
using B-do
ysis of
lopment of
90
rgy during
ot technique
ot techniqu
ot technique
Conventio
f a New Co
angular su
e No. 1
e No. 3
e No. 2
onal Con
ombined Co
uppression
ntrollers a
ontroller
and

110. Ch
Figure
hapter 5
e (5-15) reqquired dipo
(a)u
(b)u
(c)u
Analy
Devel
ole moment
using B-do
using B-do
using B-do
ysis of
lopment of
91
t to suppre
ot technique
ot techniqu
ot technique
Conventio
f a New Co
ess the sate
e No. 1
e No. 3
e No. 2
onal Con
ombined Co
llite angula
ntrollers a
ontroller
ar velocity
and

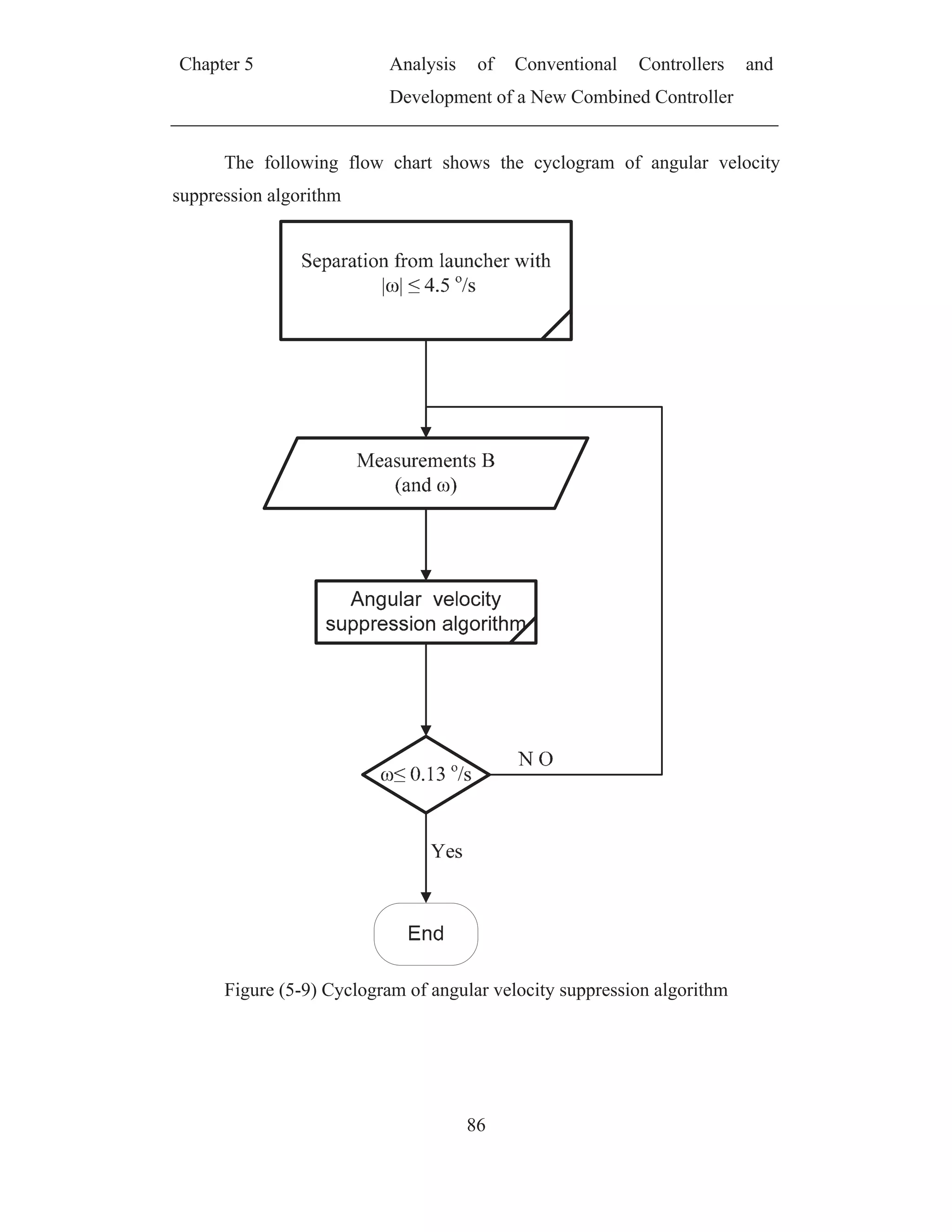
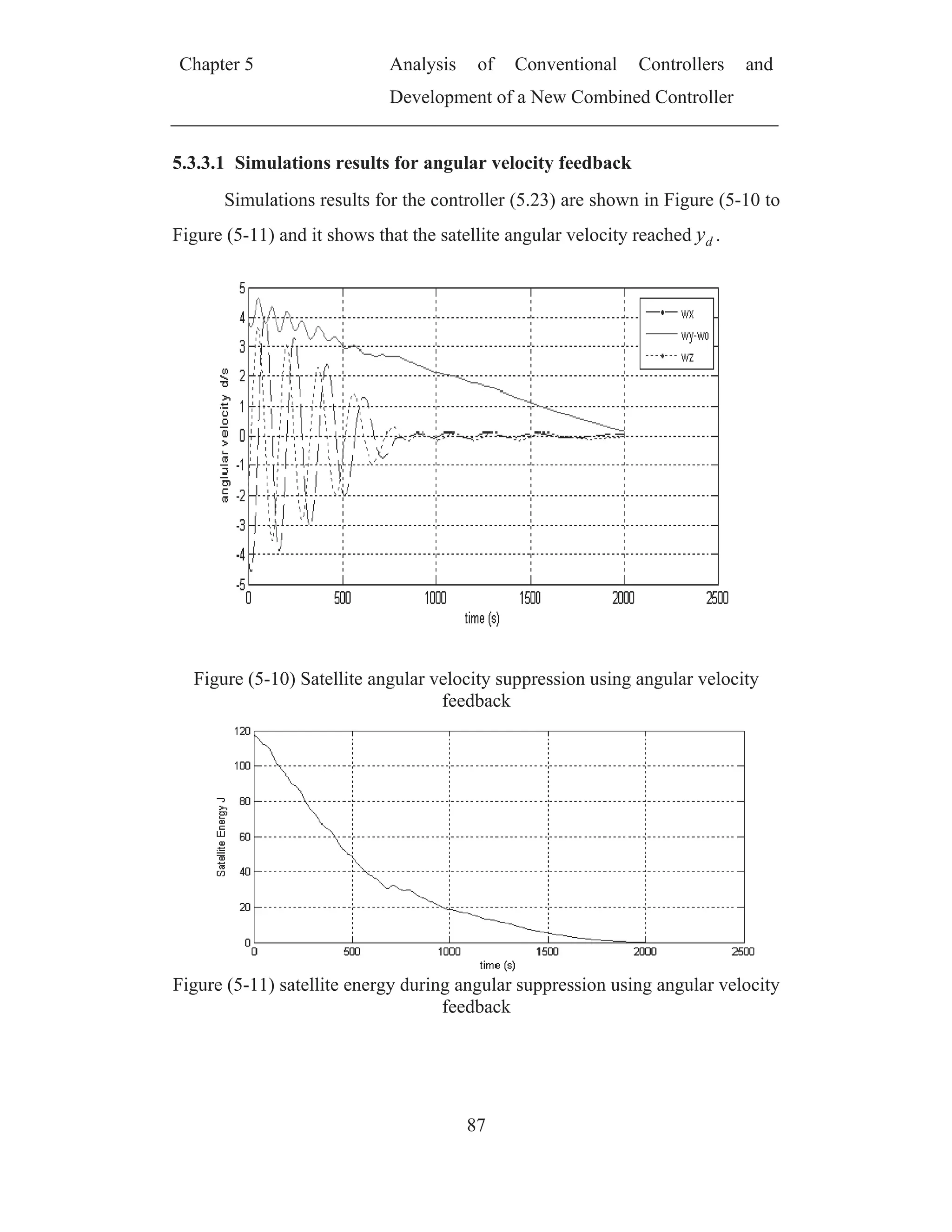
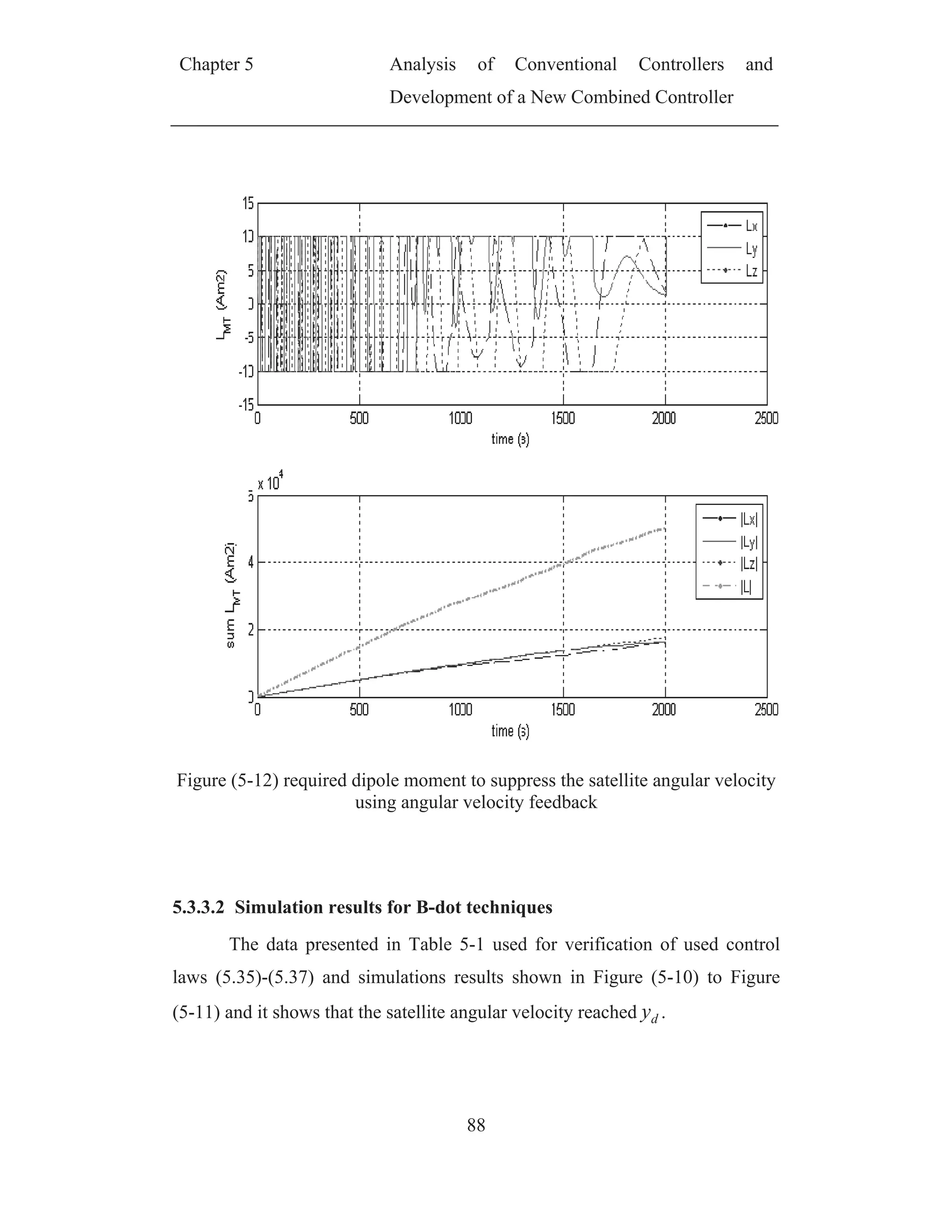
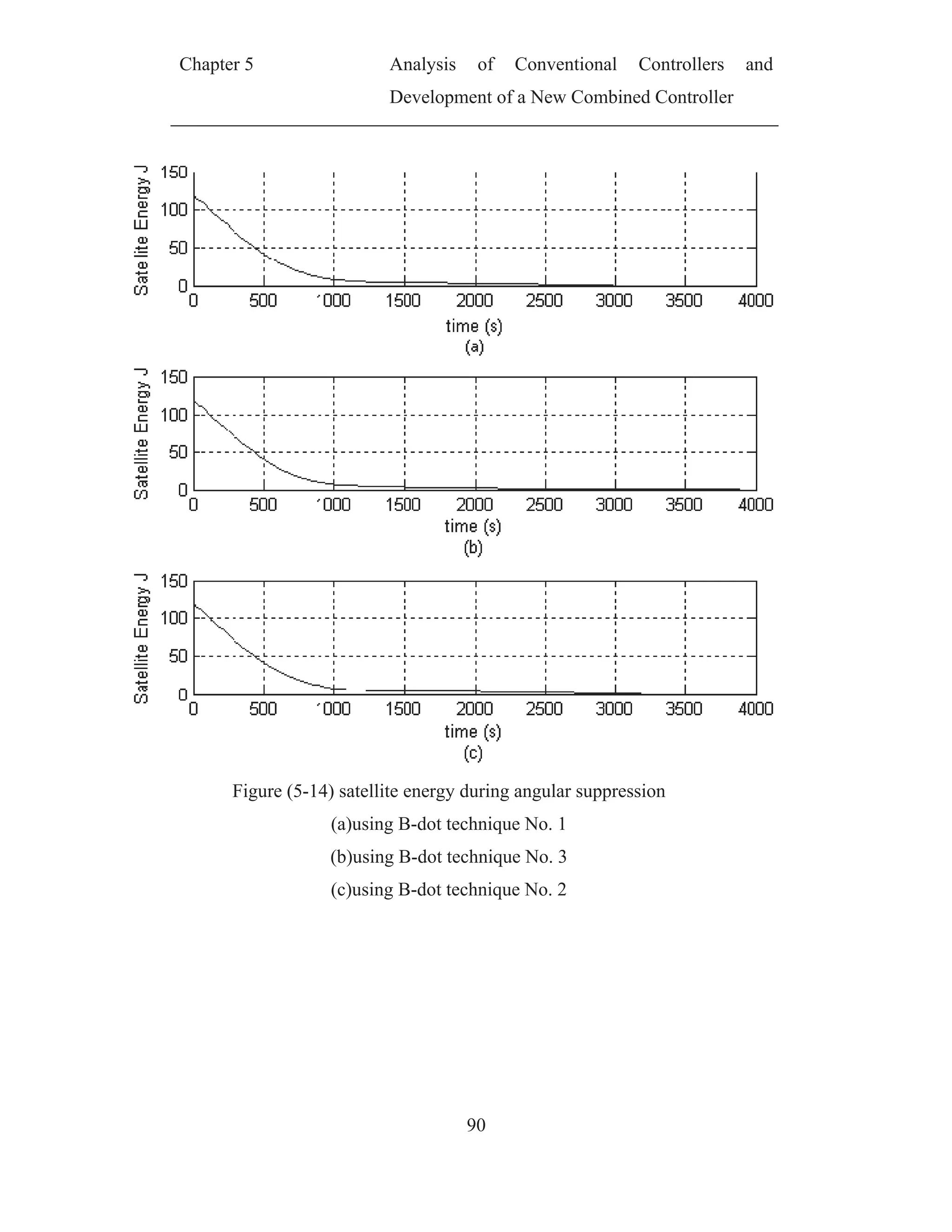
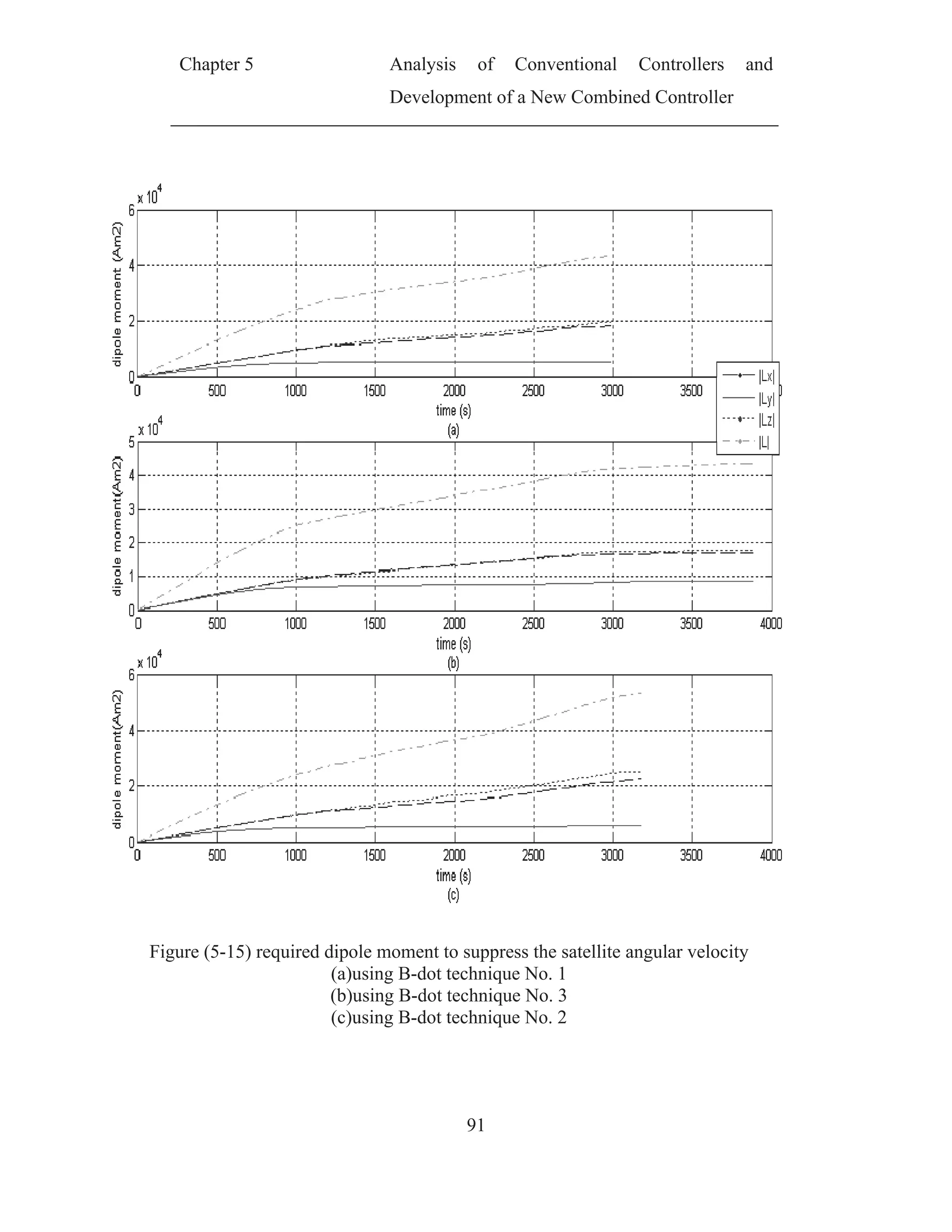
111. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
92
5.3.4 Comparison between angular velocity suppression algorithms
A comparison between performance , execution characteristics and cost
for the above mentioned angular velocity suppression algorithms. In order to
show the advantages and disadvantages for each one.
The comparison parameters used for evaluation are:
1. The required time to finish the angular velocity suppression (i.e.
sy o
/13.0 ), supT .
2. Required dipole moment until finishing angular velocity suppression,
supL .
3. The calculation time for one cycle of the algorithm calT
4. Qualitative the estimation cost .
For the calculation time for one cycle of the algorithm the following
environments was used for the evaluation.
Algorithm was developed and run using Borlandc 3.11.
Run on PC with Pentium (D) CPU 3.40 GHz. With 1 GB RAM
Used operating system XP SP2
The following table summaries the comparison results
Table 5-2the comparison result between angular velocity suppression
algorithms
Angular
velocity
feedback
B-dot
Technique
No1
Technique
No2
Technique
No3
acqT [s] 2004 2988 3885 3181
acqL [Am2
] 5.002e4 4.363e4 4.336e4 5.344e4
calT [s] 4.396e-6 3.605e-6 3.287e-6 1.4305e-4
cost Need MM and
Gyros
Need MM
and Gyros
Need MM
only
Need MM
only

112. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
93
Results conclusion
The above comparison table showed that
1. B-dot technique No. 2 is the simplest (i.e. calculation time is the
smallest one) , lowest power consumption and need MM only but it
need largest time to achieve the angular velocity suppression.
2. Angular velocity feedback algorithms could achieve angular suppression
very fast but it consumes high power compared with B-dot technique
No.1 and No. 2
3. B-dot technique No. 1 comes in the middle in calculation resources and
power consumption.
4. B-dot technique No. 3 comes in the middle in the required time to
achieve angular suppression and low cost but it is the highest power
and calculation time
5.4 Attitude acquisition and stabilization algorithms
After angular velocity suppression, satellite may have arbitrary
orientation (i.e. BCS of the satellite may not co-onside with the OCS).
Therefore, it is required to make attitude acquisition or reorient the satellite in
order to make the satellite nadir pointing (i.e. to make BCS of the satellite co-
onside with the OCS), after that it is needed to make attitude stabilization or
keeping the satellite at nadir pointing. To make attitude acquisition and
stabilization, the used control algorithm must conation information about the
satellite attitude and angular velocity. Commonly there are three methods used
for attitude acquisition and stabilization
1. PD-Like Controller
2. Sliding Mode Controller
3. Linear Quadratic Regulator

113. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
94
In the next subsections, adscription for the above mentioned controllers
and simulation results will be presented then comparison between them will be
introduced.
5.4.1 PD-Like Controller
Three axes attitude control requires accurate attitude knowledge to
function correctly. So PD-like controller [12] will be used, here the feedback
from relative angular velocity is used instead of the derivative of
quaternion[24]. Therefore, the algorithm itself becomes just a simple rate and
position feedback; hence the required magnetic torque can be calculated as
follows
pvc kykT (5.39)
Where
vk Positive rate gain constant
pk Positive position gain constant
And the required dipole moment will be
2
B
TB
L c
(5.40)
For this controller, the attitude and angular velocity are fed back into the
system
Function diagram of PD-like controller is shown below

114. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
95
2
B
TB
L
KyKTc
C
pv
Figure (5-16) Function diagram of attitude acquisition and stabilization using
PD-like controller
5.4.1.1 Checking the stability of PD-Like Controller
To check the stability of the PD like controller (5.39), let us reconsider
the candidate Lyapunov function mentioned in(5.10) plus
))1(( 2
o
T
pK

115. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
96
))1((
)(
2
1
)(
2
3
2
1
))1((
2
22
2
o
T
p
T
yyozz
T
o
T
o
T
ptot
K
enJenJJerJeryJy
KEV
(5.41)
Since, the attitude quaternion satisfies the constraint equation
1
2
o
T
))1(2
)(
2
1
)(
2
3
2
1 22
op
T
yyozz
T
o
T
K
enJenJJerJeryJyV
(5.42
)
Therefore, the derivative of Lyapunov function can be easily calculated
using (4.39) and (5.22)
T
pc
T
ykTyV (5.43)
Substituting (5.39)in (5.43)
yky
ykkykyV
v
T
T
ppv
T
)(
(5.44)
0V (5.45)
Thus the satellite with control law (5.39) would be globally
asymptotically stable at nadir pointing (i.e. at the reference )}0,0(:),{(y )
5.4.2 Sliding Mode Controller
A sliding mode controller is implemented for the attitude corrections
using magnetic actuator . Full attitude information in the form of the attitude
quaternion and the satellite relative angular velocity y are used as feedback

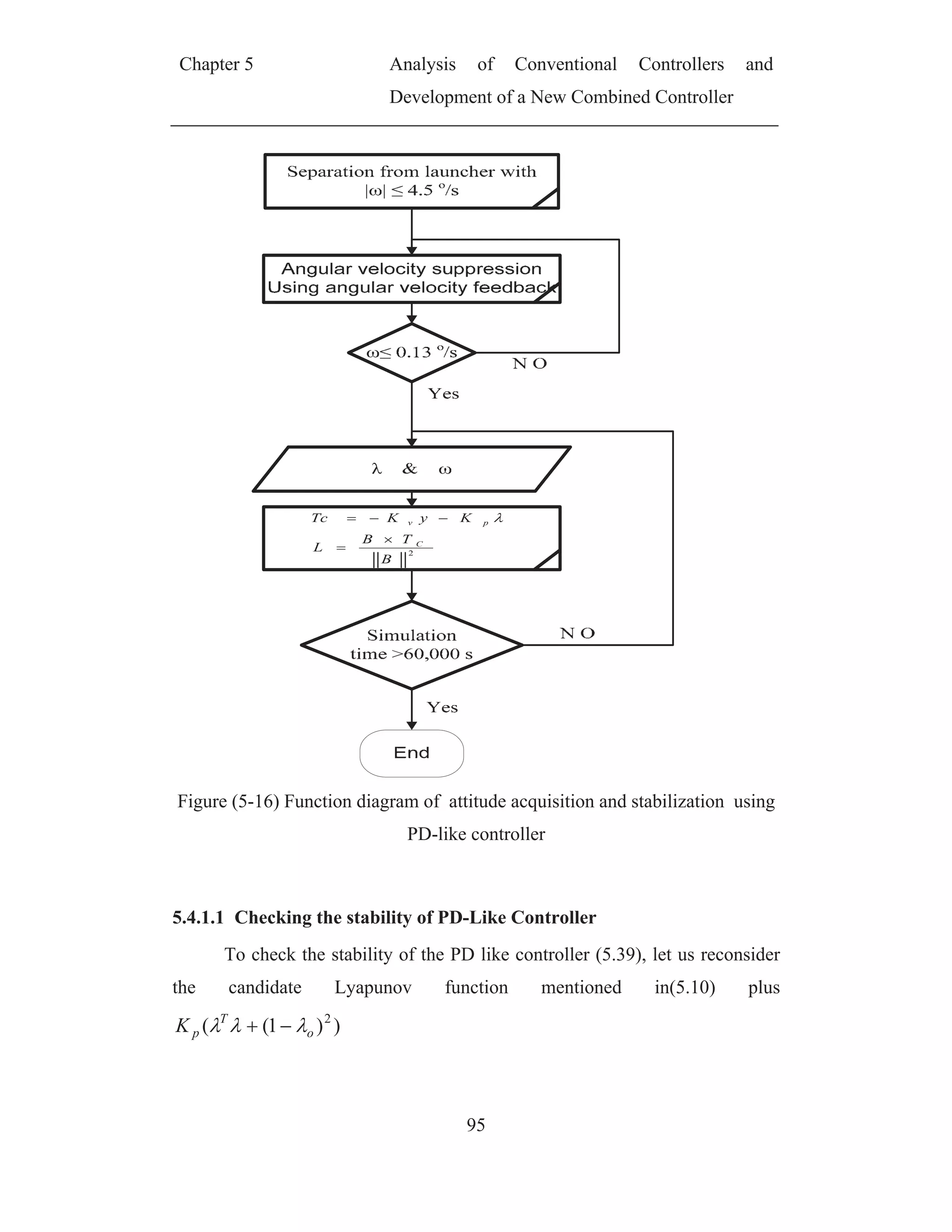
116. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
97
signals. The objective of the attitude control is to get nadir pointing; the design
strategy of the sliding mode controller consists of two steps,
1. Sliding manifold design.
2. Sliding condition design.
The description and design of skidding mode controller are based on
[20]
5.4.2.1 Sliding Manifold Design
Consider manifold, a 3 dimensional hyper plane, in the state space of a
6th order system
T
y .The sliding manifold is designed in such a way that the
satellite trajectory, if on the hyper plane, converges to the reference. However,
the satellite motion is not confined to the 3 dimensional hyper plane in general.
Therefore, a control law forcing the satellite motion toward the manifold is
necessary for achieving stable satellite motion
Let a sliding variable s be defined as in
qAyJs (5.46)
Where qA
is a positive definite matrix.
The sliding manifold is the subspace of the state space, where the sliding
variable equals
}0:,{ syS (5.47)
The definition of the sliding variable,s , guarantees convergence of to
zero with an exponential rate. To prove this statement, consider a Lyapunov
candidate function
)1(2
)1( 2
o
o
T
V
(5.48)
The time derivative of the Lyapunov candidate function is calculated
applying the kinematics
yV T
(5.49)

117. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
98
But qAy thus
q
T
AV (5.50)
The time derivative of the Lyapunov function is negative definite, since
qA is positive definite matrix. According to Lyapunov’s direct method the
equilibrium 1,0,0 oy is asymptotically stable if the satellite is on the
sliding manifold S
5.4.2.2 Sliding Condition Development
The sliding condition keeps decreasing the distance from the state to the
sliding manifold, such that every solution ,y originating outside the sliding
manifold tends to it. Now the manifold is an invariant set of the satellite motion
and the trajectory of the system converges to the reference.
The result of the sliding condition design will be a desired control torque
dT . When the desired control torque is implemented the satellite trajectory
converges to the sliding manifold, but due to the satellite, motion is stable on
the sliding manifold, its trajectory converges to the reference.
So the objective Sliding Condition Development is to derive the desired
control torque dT turning the satellite trajectory towards the sliding manifold.
The representation of the satellite motion in the space of the sliding variable is
calculated by differentiation of the sliding variable, )(ts w.r.t. time, which
describes projection of the satellite motion on the space of the sliding variable
(the s-space)
qo AneJJs (5.51)

118. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
99
The derivatives of the satellite angular velocity and the attitude
quaternion are calculated according to the equations of kinematics and
dynamics,(4.31),(4.43).
coqo TyyAyenJJererJs )(
2
1
)(3 2
(5.52)
Assume that the satellite trajectory is on the sliding manifold. An
equivalent torque eqT is a control torque necessary to keep the satellite on the
sliding manifold. In other words, if the control torque cT is equal to the
equivalent torque eqT then the time derivative of the sliding variable equals zero.
If the satellite is not on the sliding manifold, a desired control torque dT equals
the sum of the equivalent torque eqT and a part making the sliding variable
converge zero [20]
)(ssignATT seqd (5.53)
Where
sA is a positive definite matrix and
)(
2
1
)(3 2
yyAyenJJererJT oqoeq (5.54)
And according to[20]
2
B
TB
L d
(5.55)
The Block diagram of attitude acquisition and stabilization using sliding
mode is shown below

119. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
100
qAyJs
Figure (5-17) Block diagram of attitude acquisition and stabilization using
sliding mode
5.4.3 Linear Quadratic Regulator
The satellite dynamics are quite nonlinear, but about the reference a
linear approach to control design is attractive. Traditionally LQR (Linear
Quadratic Regulator) has been used on magnetic actuated satellites because of
their reliability and robustness. The LQR strategy is based on linearizing the
systems dynamics, defining an object function which shall be minimized and
generate a gain matrix which is used for feedback. For more details on LQ-
control problems see [20],[27].

120. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
101
The linearization of the satellites attitude was derived in section 4.2.3
recalling the system of differential equation that describe the linear mode of the
satellite (4.61)
)().()(.)( tLtFtxAtx
(5.56)
Where matrices Aand )(tF are defined in (4.63) and (4.65)
The cost function which should be to minimized is[25]:
dtuPuxQxJ
T
to
op ]....[
(5.57)
The matrices Q and P are positive semidefinite and are used to weight
state and actuator usage. The solution to the LQ-problem is given by the Ricatti
equation
QtRtFPtFtR
tRAAtRtR
ric
T
ric
ric
T
ricric
)()()()(
)()()(
1
(5.58)
The solution of the LQR problem yields the time varying controller
)()()()( 1
txtRtFPtL ric
T
(5.59)
The block diagram of LQR is shown below

121. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
102
Figure (5-18 )Block diagram of attitude acquisition and stabilization using
LQR
5.4.4 Simulation verification
For verification of attitude acquisition and stabilization algorithms it is
considered the initial value is the same in Table 5-1 and the angular velocity
suppression will be done using angular velocity feedback algorithm. It is also
considered that the attitude acquisition phase is finished when
sy oo
/02.0,10 where is the satellite attitude with respect OCS and

122. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
103
the simulation time will be 10 orbital period or 60,000 sec in order to
investigate the satellite steady state behavior under the effect of external
disturbance .The following flowchart shows Cyclogram of attitude acquisition
and stabilization algorithm
Figure (5-19) Cyclogram of attitude acquisition and stabilization algorithm

123. Ch
5.4.
Figu
kep
Fig
velocity
controller
hapter 5
.4.1 Simu
Simula
ure (5-22 a
pt nadir poi
gure (5-20
feedback,
r
lations res
ations resul
and it show
inting again
0) Satellite
followed
Analy
Devel
sults for P
lts for the c
ws that the
nst the exte
response
d by, attit
ysis of
lopment of
104
PD-like con
controller (
satellite ac
ernal distur
during ang
tude acqui
Conventio
f a New Co
ntroller
(5.39) are s
chieved the
rbances.
gular velo
isition and
onal Con
ombined Co
shown in F
e attitude a
city suppr
d stabiliza
ntrollers a
ontroller
Figure (5-2
acquisition
ession usin
ation usin
and
20 to
and
ng angular
ng PD-like
r
e

124. Ch
Fig
using ang
PD-like c
hapter 5
gure (5-21
gular veloc
controller
1) Zoom in
city feedba
Analy
Devel
n for satel
ack, follow
ysis of
lopment of
105
llite respon
wed by, att
Conventio
f a New Co
nse during
titude acqu
onal Con
ombined Co
g angular
uisition an
ntrollers a
ontroller
velocity su
nd stabiliza
and
uppression
ation using
n
g

125. Ch
Fig
using ang
using PD
5.4.
to F
and
hapter 5
gure (5-22
gular veloc
-like contr
.4.2 Simu
Simula
Figure (5-2
d kept nadir
2) Require
city feedba
roller
lations res
ations resul
25) and it s
r pointing a
Analy
Devel
d dipole m
ack, follow
sults for sl
lts for the
shows that
against the
ysis of
lopment of
106
moment du
wed by, at
liding mod
controller
the satellit
e external d
Conventio
f a New Co
uring angu
ttitude acq
de controll
(5.59) are
te achieved
disturbance
onal Con
ombined Co
ular veloci
quisition an
ler
e shown in
d the attitu
es.
ntrollers a
ontroller
ity suppres
nd stabiliz
Figure (5
ude acquisi
and
ssion
ation
-23)
ition

126. Ch
Fig
velocity f
controller
hapter 5
gure (5-23
feedback,
r
) Satellite
followed b
Analy
Devel
response d
by, attitude
ysis of
lopment of
107
during ang
e acquisitio
Conventio
f a New Co
gular veloc
on and sta
onal Con
ombined Co
city suppre
abilization
ntrollers a
ontroller
ession usin
using slid
and
ng angular
ding mode

127. Ch
Fig
using ang
sliding m
hapter 5
gure (5-24
gular veloc
mode contro
4) Zoom in
city feedba
oller.
Analy
Devel
n for satell
ck, follow
ysis of
lopment of
108
ite respons
ed by, attit
Conventio
f a New Co
se during a
tude acqui
onal Con
ombined Co
angular ve
sition and
ntrollers a
ontroller
elocity supp
stabilizatio
and
pression
on using

128. Ch
Fig
angular v
sliding m
5.4.
to F
and
hapter 5
gure (5-25
velocity fe
mode contro
.4.3 Simu
Simula
Figure (5-2
d kept nadir
) Required
eedback, f
oller
lations res
ations resul
28) and it s
r pointing a
Analy
Devel
d dipole m
followed b
sults for L
lts for the
shows that
against the
ysis of
lopment of
109
oment dur
by, attitud
LQR
controller
the satellit
e external d
Conventio
f a New Co
ring angula
de acquisit
(5.59) are
te achieved
disturbance
onal Con
ombined Co
ar velocity
tion and s
e shown in
d the attitu
es.
ntrollers a
ontroller
suppressio
stabilizatio
Figure (5
ude acquisi
and
on using
on using
-26)
ition

129. Ch
Fig
velocity f
hapter 5
gure (5-26
feedback, f
6 Satellite r
followed by
Analy
Devel
response d
y, attitude
ysis of
lopment of
110
during ang
acquisition
Conventio
f a New Co
gular veloc
n and stabi
onal Con
ombined Co
city suppre
lization us
ntrollers a
ontroller
ession usin
ing LQR
and
g angular

130. Ch
Fig
using ang
using LQ
hapter 5
gure (5-27)
gular velo
QR
) Zoom in
city feedb
Analy
Devel
for satellit
back, follow
ysis of
lopment of
111
te response
wed by, a
Conventio
f a New Co
e during an
attitude acq
onal Con
ombined Co
ngular veloc
quisition a
ntrollers a
ontroller
city suppre
and stabiliz
and
ession
zation

131. Ch
Figure (5
angular v
LQR
5.4.
abo
sho
hapter 5
5-28) Requ
velocity fe
.5 Comp
algori
A comp
ove mentio
ow the adva
The co
5. The
0
6. Requir
uired dipo
edback, fo
parison b
ithms
parison bet
oned attitud
antages and
mparison p
required
y .0,1.
red dipole m
Analy
Devel
ole momen
ollowed by
between
tween perf
de acquisit
d disadvan
parameter u
time to
so
/02. ), T
moment un
ysis of
lopment of
112
nt during a
y, attitude
attitude
formance a
tion and s
ntages for e
used for ev
finish
acqT .
ntil finishin
Conventio
f a New Co
angular ve
acquisition
acquisitio
and executi
tabilization
each one.
valuation a
the attit
ng the attitu
onal Con
ombined Co
elocity sup
n and stab
on and
ion charact
n algorithm
are :
tude acq
ude acquis
ntrollers a
ontroller
ppression u
bilization u
stabiliza
teristics for
ms in orde
quisition
ition, acqL
and
using
using
tion
r the
er to
(i.e.
.

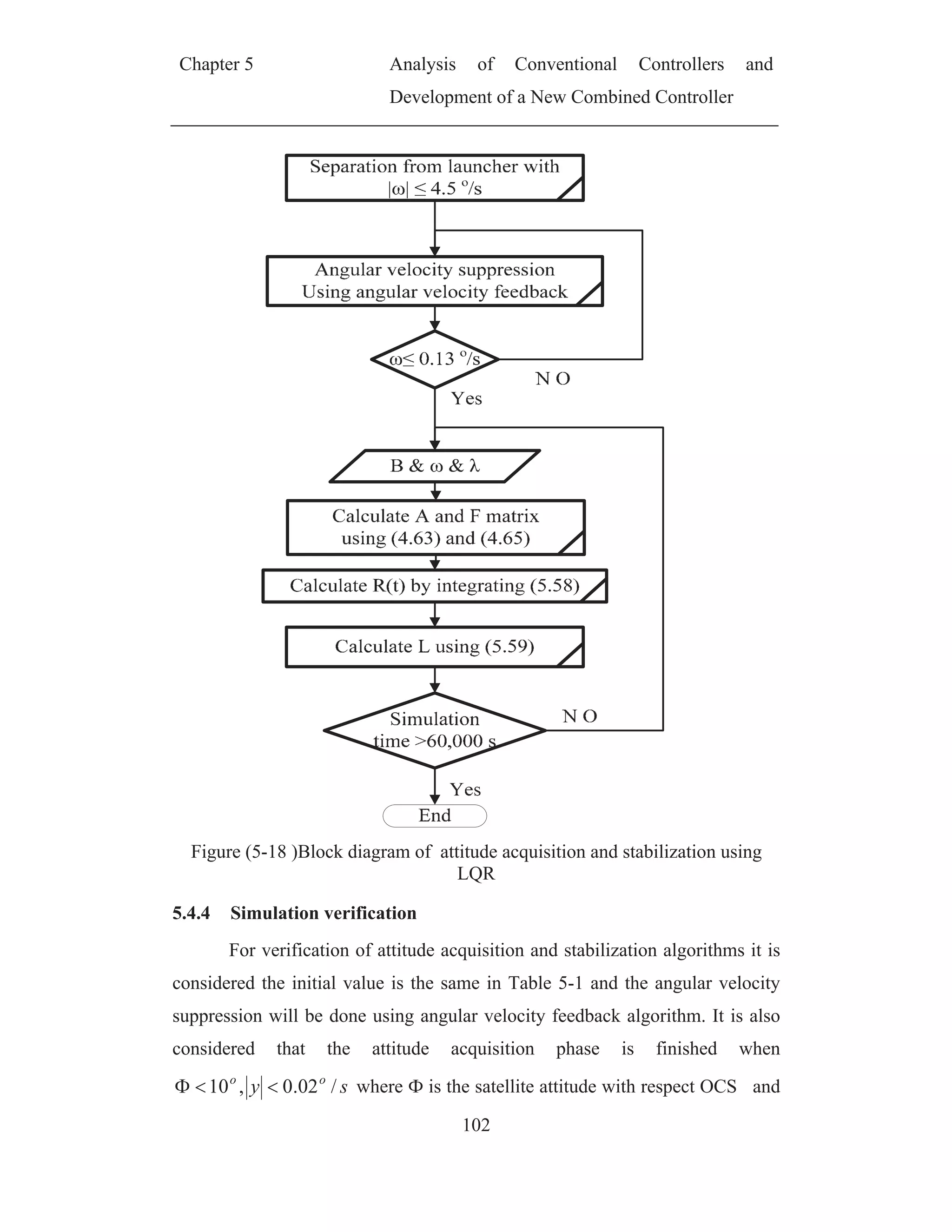
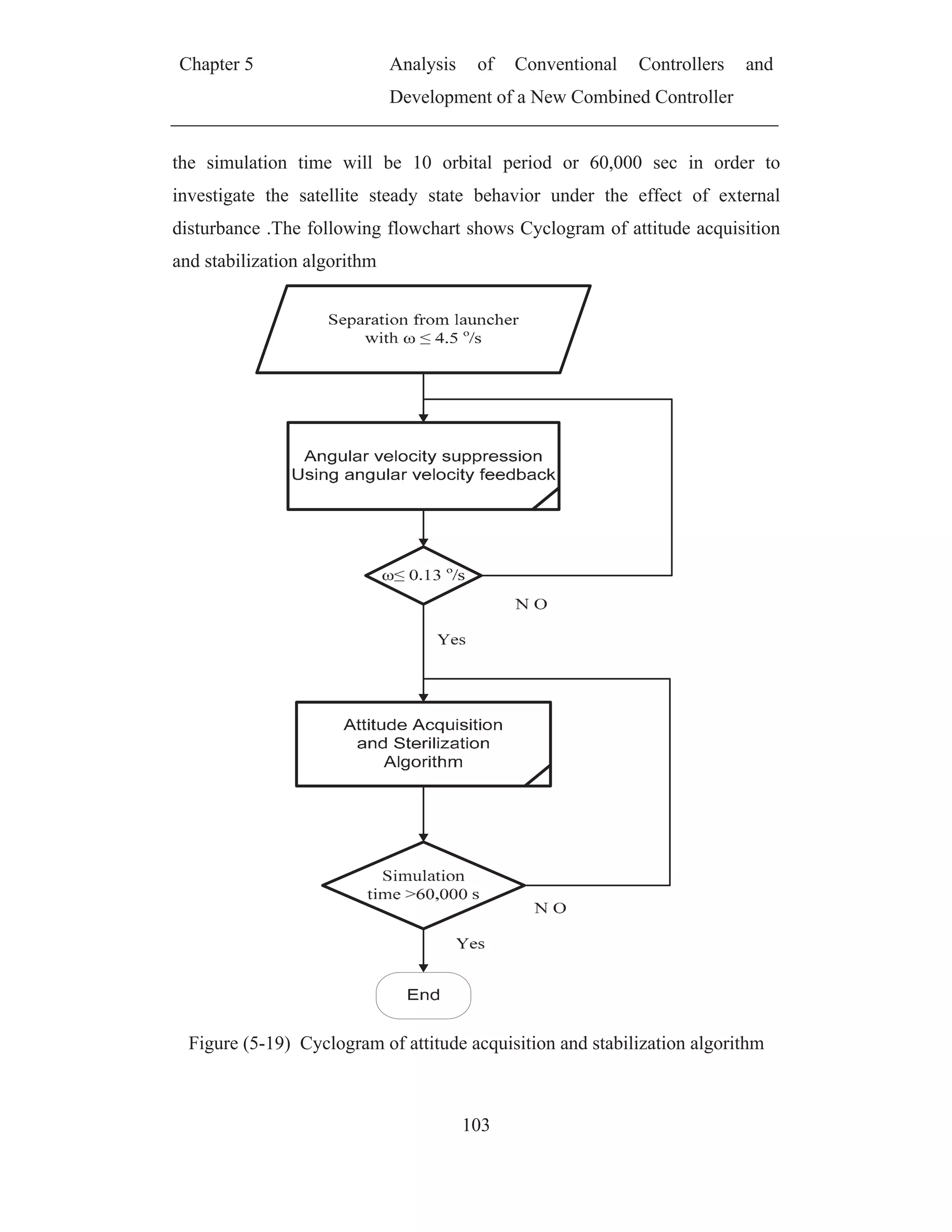
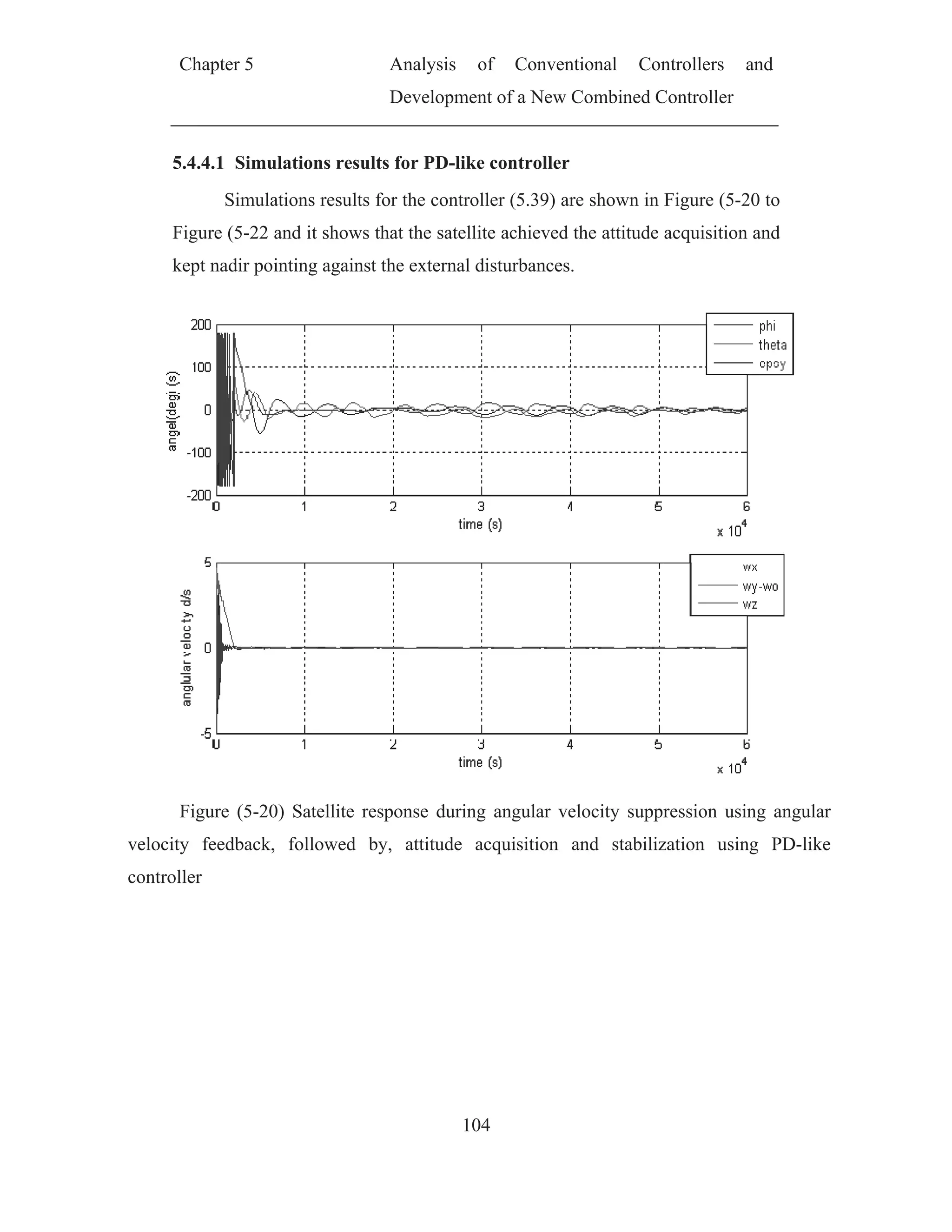
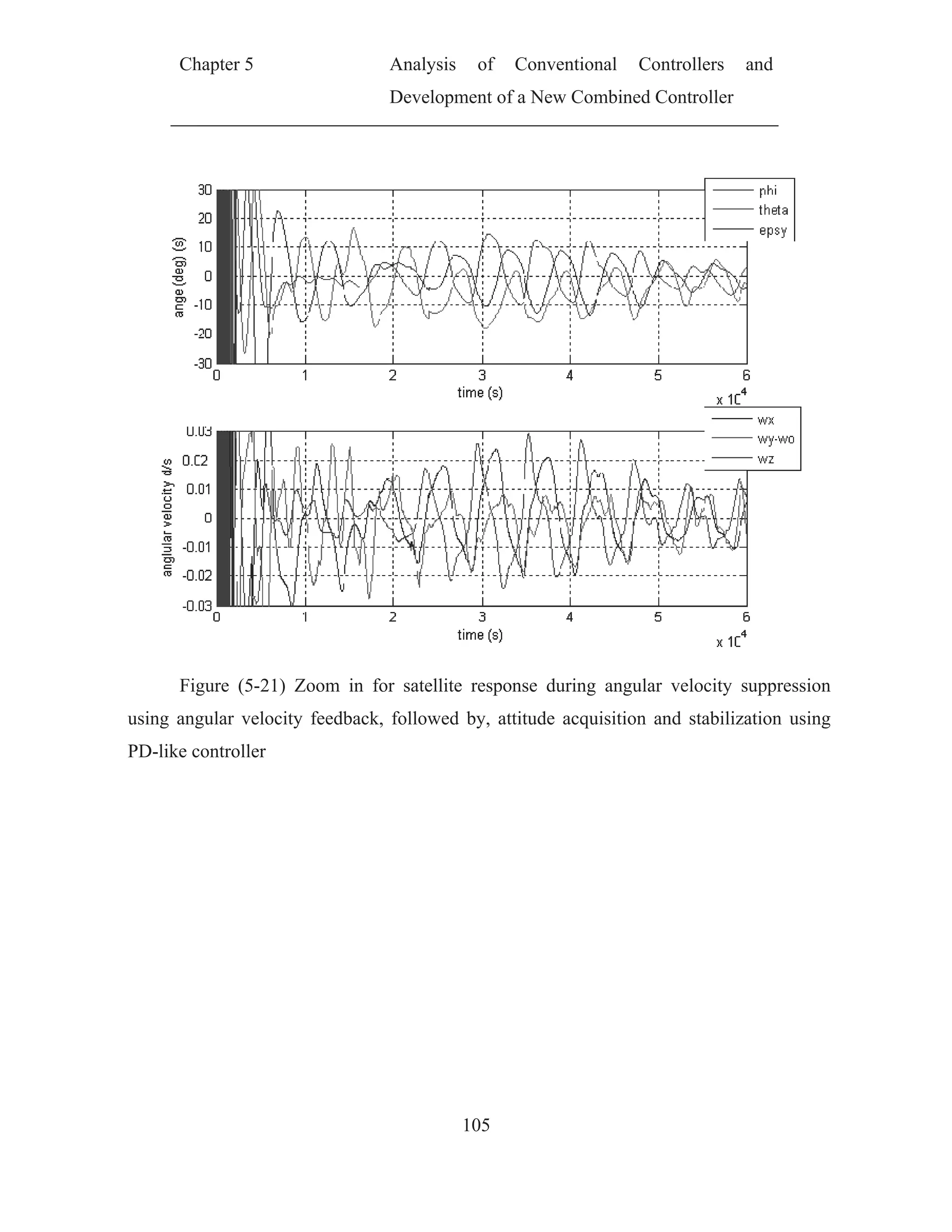
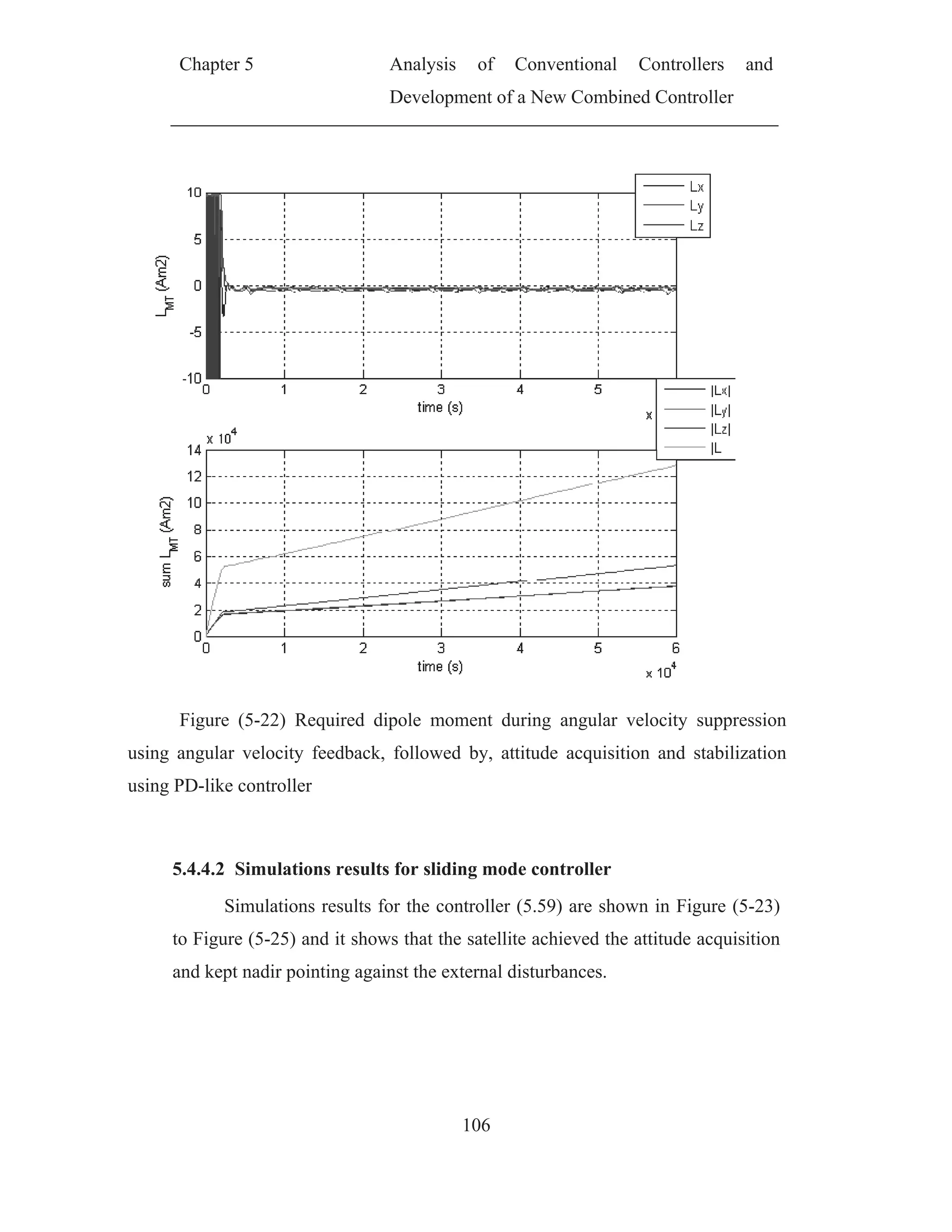
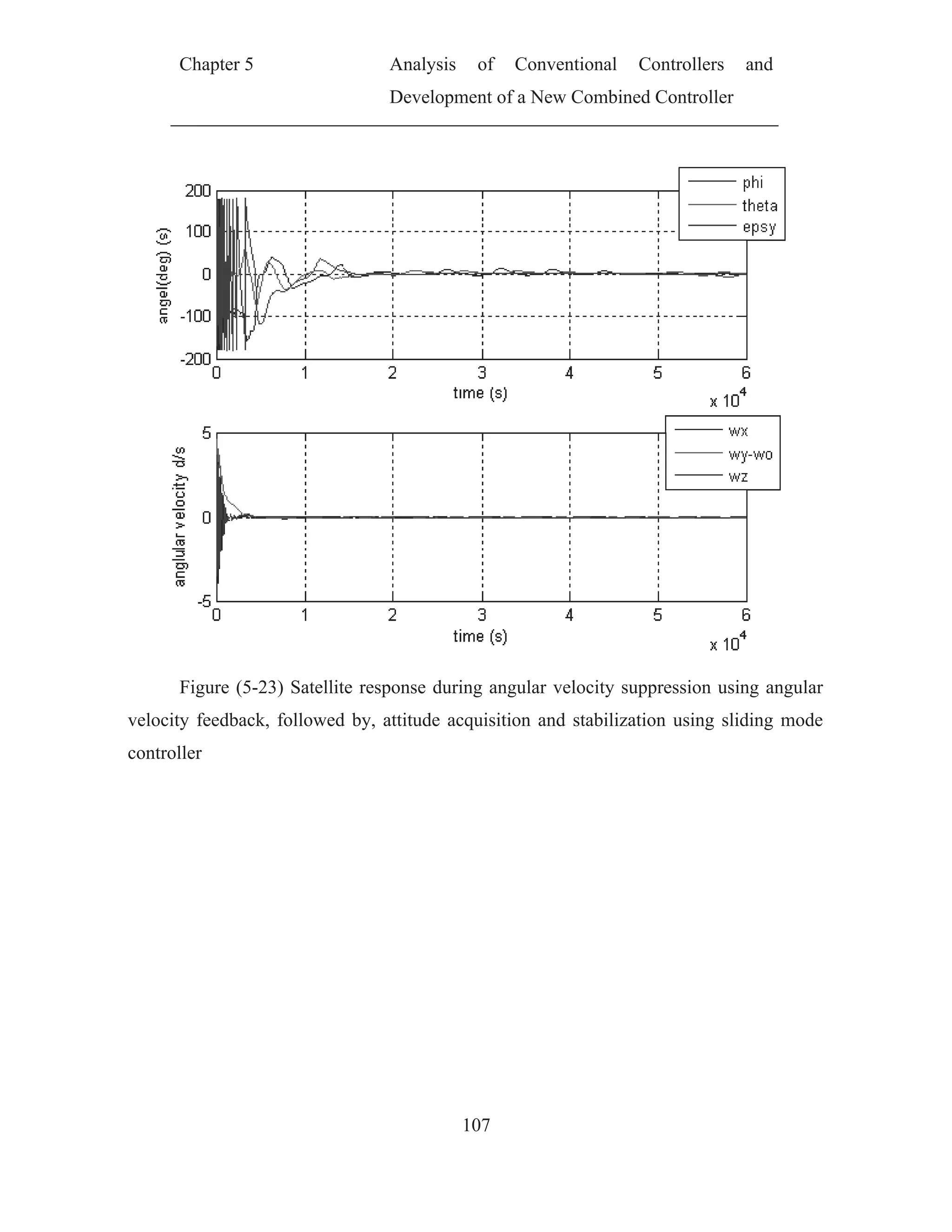
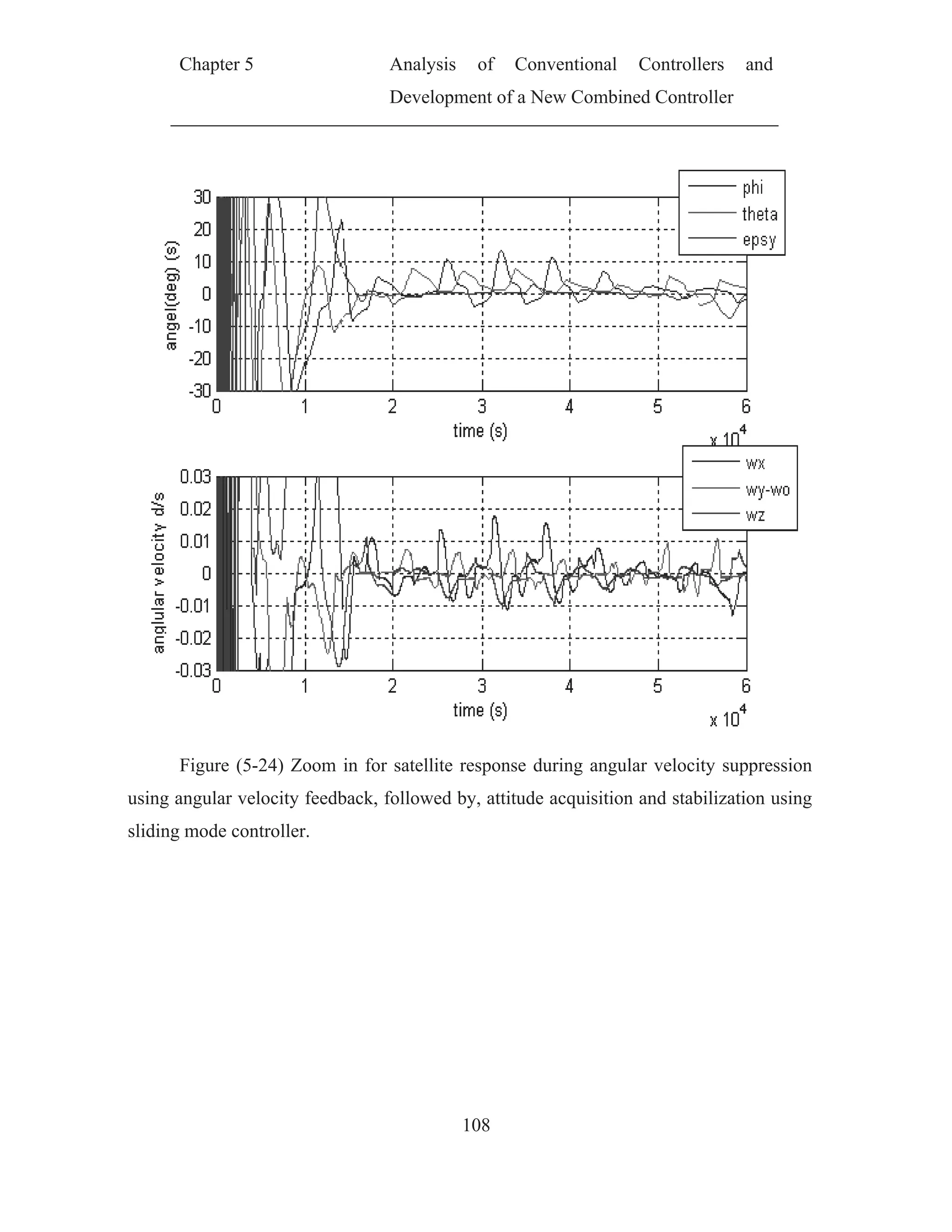
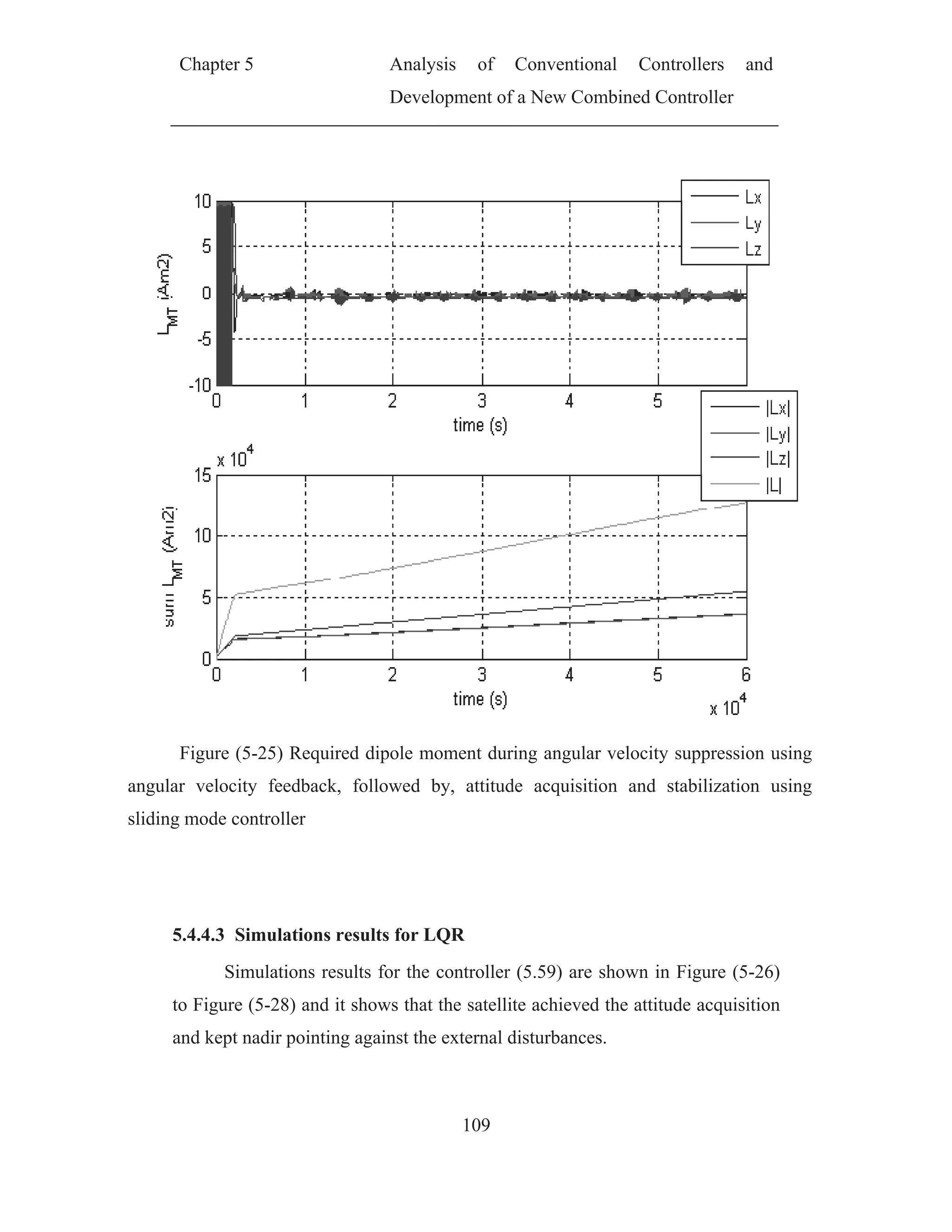
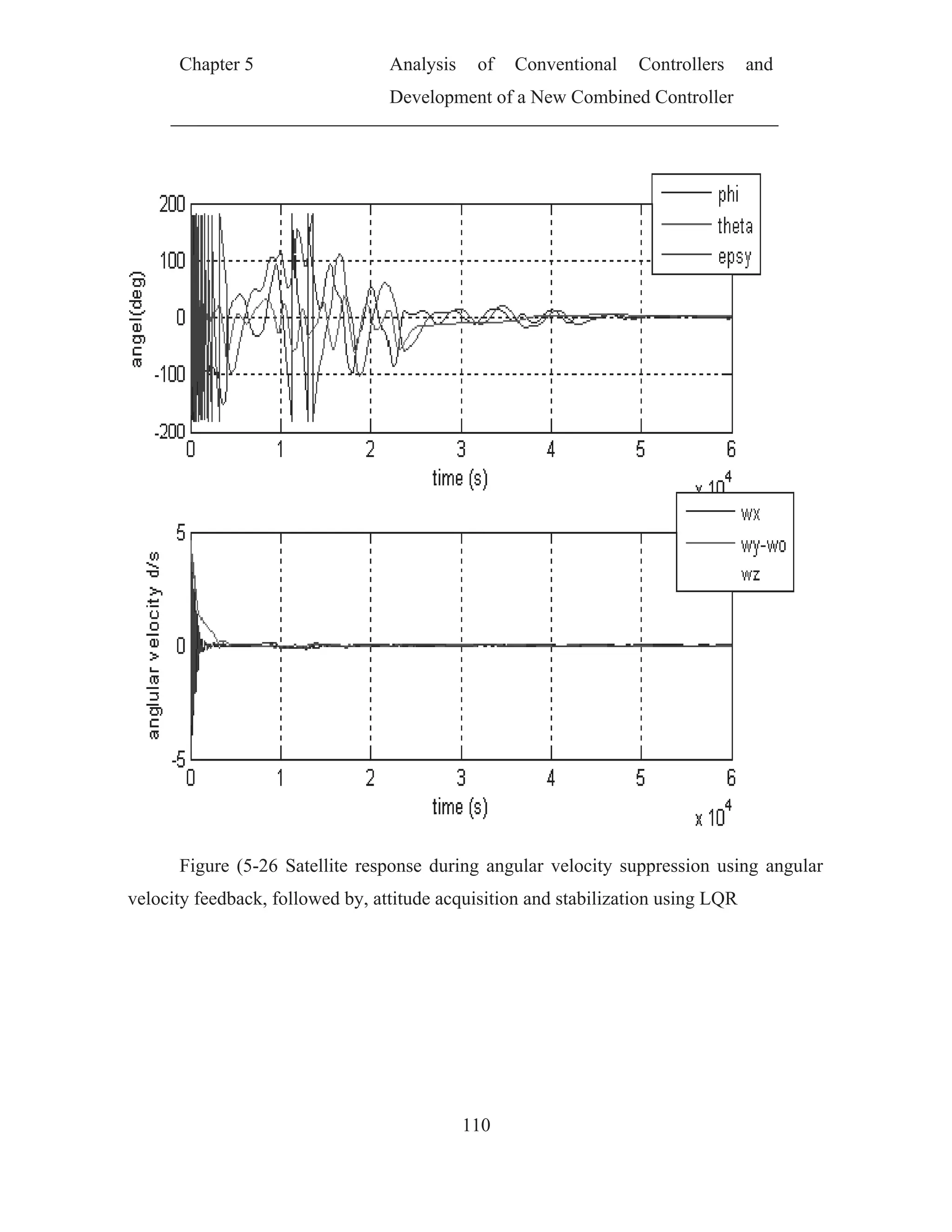
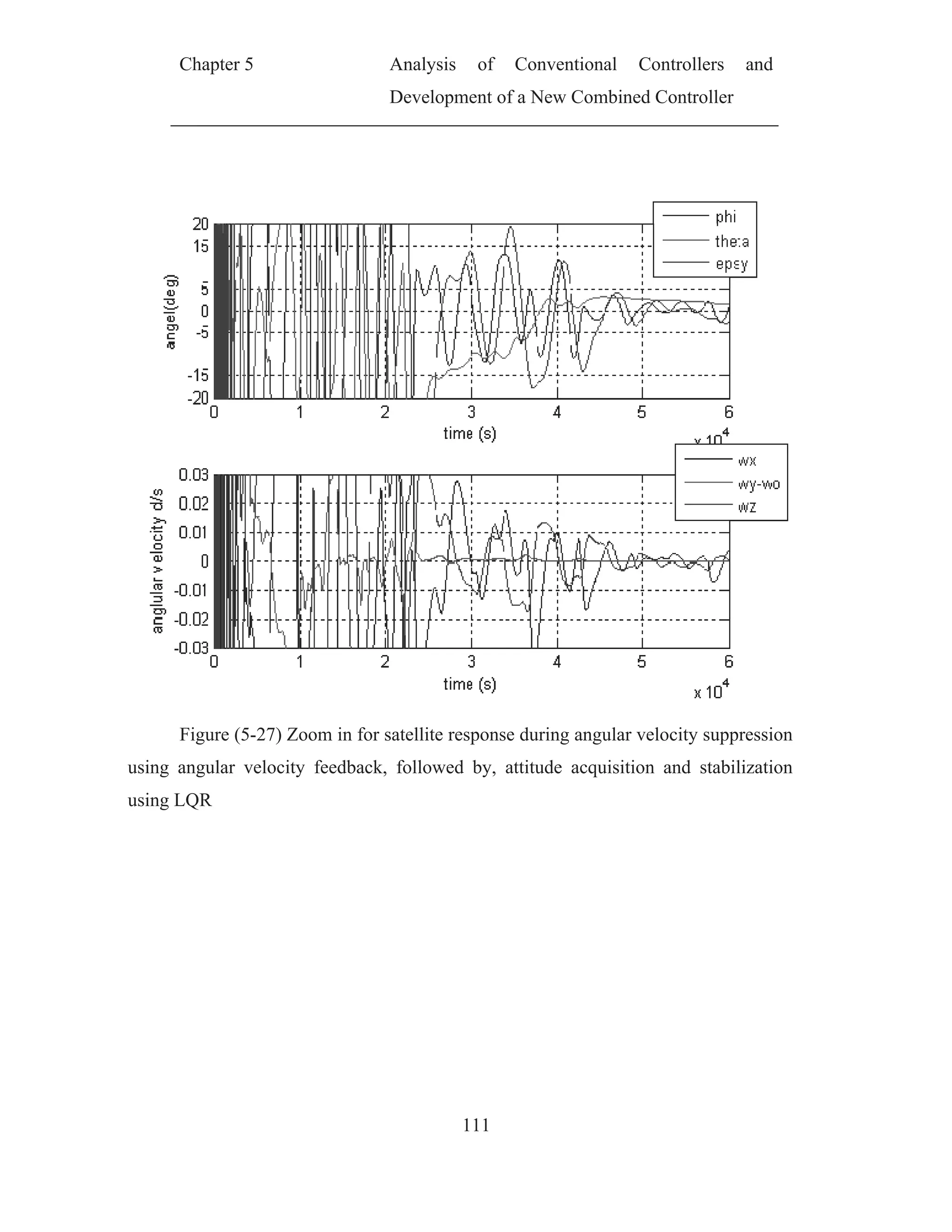
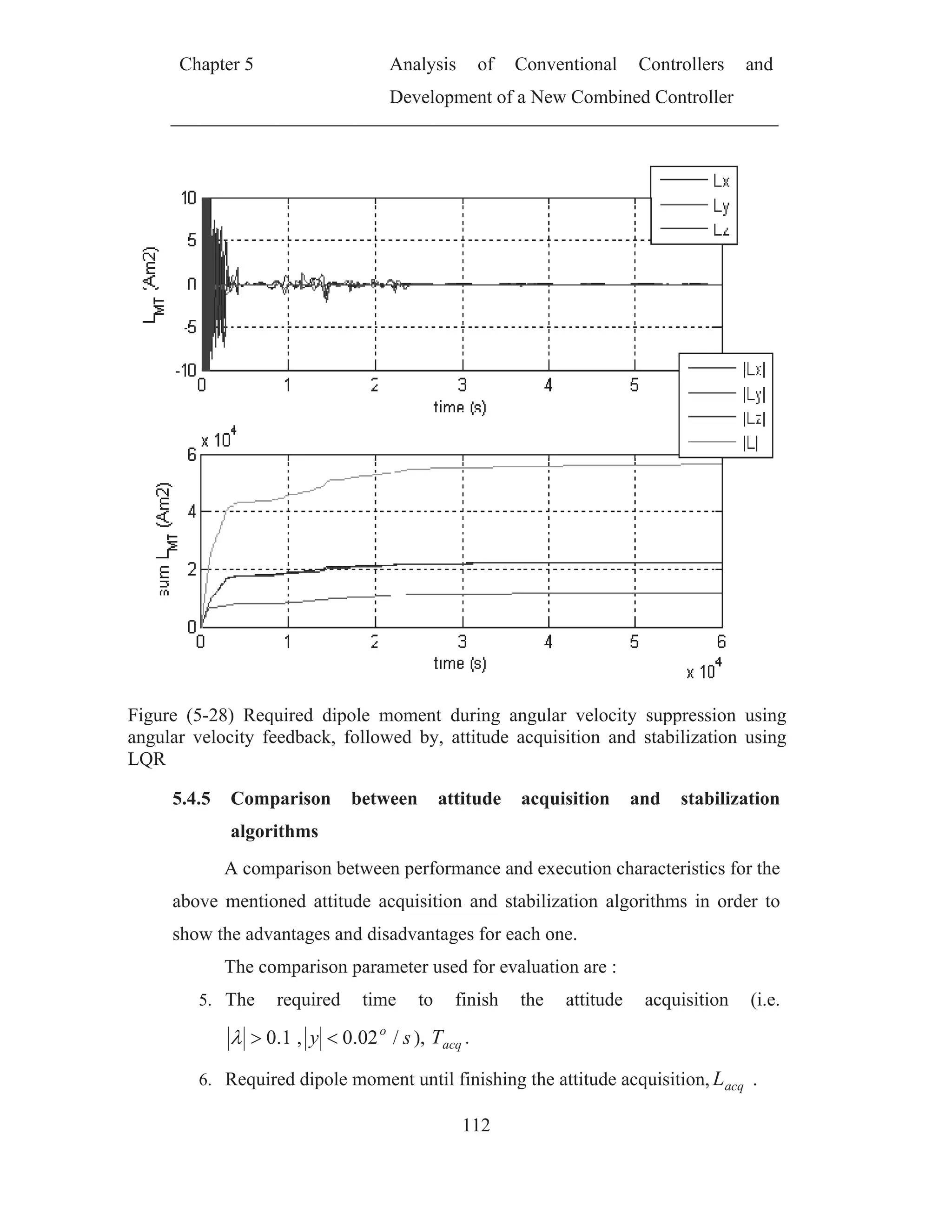
132. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
113
7. The total dipole moment required during 10 orbital period totL
8. The steady stat error for angels and angular velocity ssss EE , .
9. The calculation time for one cycle of the algorithm calT
For the calculation time for one cycle of the algorithm the following
environments was used for the evaluation.
Algorithm was developed and run using Borlandc 3.11.
Run on PC with Pentium (D) CPU 3.40 GHz. With 1 GB RAM
Used operating system XP SP2
The following table summarizes the comparison results
Table 5-3the comparison result between attitude acquisition and stabilization
algorithms
PD-like controller
Sliding Mode
controller
LQR
acqT [s] 5,754 9,609 25,340
acqL [Am2
] 5.658e4 6.259e4 5.480e4
calT [s] 4.451e-6 6.091e-6 3.539e-3
totL [Am2
/s] 12.84e4 12.99e4 5.652e4
ssE [deg.] ±10 ±7 ±4
ssE [deg./s] ±0.013 ±0.011 ±0.008
Results conclusion
The above comparison table showed that
1. PD-like controller is the simplest (i.e. calculation time is the smallest
one ) algorithm and could achieve attitude acquisition very fast but
needs large dipole moments during stabilization and give low accuracy
2. the LQR is very useful to save the consumed power by MT specially
during the stabilization period and give very high accuracy but needs
high calculation resources and it is not suitable for attitude acquisition.

133. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
114
3. the sliding mode comes in the middle in calculation resources and
achieved accuracy but need the largest power during stabilization
5.5 Combined attitude control
As conclusion from the above comparisons between the different
magnetic attitude control algorithms used during angular suppression, attitude
acquisition and attitude stabilization, we cold conclude the following facts
1. if we consider that the comparison parameters in Table 5-2 are equally-
weighted, then the B-dot technique No2 will be the best one for angular
velocity suppression
2. if we consider that the above comparison parameters in Table 5-3 are
equally- weighted, beside acqT , acqL , calT as evaluation parameters for
attitude acquisition, Then, the PD-like is the best one for attitude
acquisition
3. if we consider that the above comparison parameters in Table 5-3 are
equally- weighted, beside tatL ssE , ssE , calT as evaluation parameters
for attitude stabilization Then, LQR is the best one for attitude
stabilization
As a results, a combined algorithm was developed as a combination
from the best algorithms in the corresponding phase.. This algorithm will
switch between the selected control algorithms according to the operation
phase (i.e. angular suppression, attitude acquisition and attitude stabilization),
based on the values of relative angular velocity and quaternion. The following
flowchart shows the cyclogram for the combined algorithm

134. Chapter 5 Analysis of Conventional Controllers and
Development of a New Combined Controller
115
Figure (5-29) S Cyclogram of the developed combined algorithm

135. Ch
5.5.
sate
exte
Fig
velocity
algorithm
hapter 5
.1.1 Simu
Simula
ellite achie
ernal distur
gure (5-30
feedback,
m
ulations re
ations resu
eved the at
rbances.
) Satellite
followed
Analy
Devel
esults for C
lts for the
ttitude acq
response d
by, attitu
ysis of
lopment of
116
Combined
e combined
quisition an
during ang
de acquisi
Conventio
f a New Co
algorithm
d algorithm
nd kept na
gular veloc
ition and
onal Con
ombined Co
m
m and it s
adir pointin
city suppre
stabilizatio
ntrollers a
ontroller
shows that
ng against
ession usin
on using c
and
the
t the
ng angular
combined

136. Ch
Fig
suppressi
stabilizati
hapter 5
gure (5-3
ion using a
ion combin
1) Zoom
angular ve
ned algorith
Analy
Devel
in for
elocity fee
hm
ysis of
lopment of
117
satellite r
dback, fol
Conventio
f a New Co
response d
llowed by,
onal Con
ombined Co
during an
, attitude a
ntrollers a
ontroller
ngular vel
acquisition
and
ocity
n and

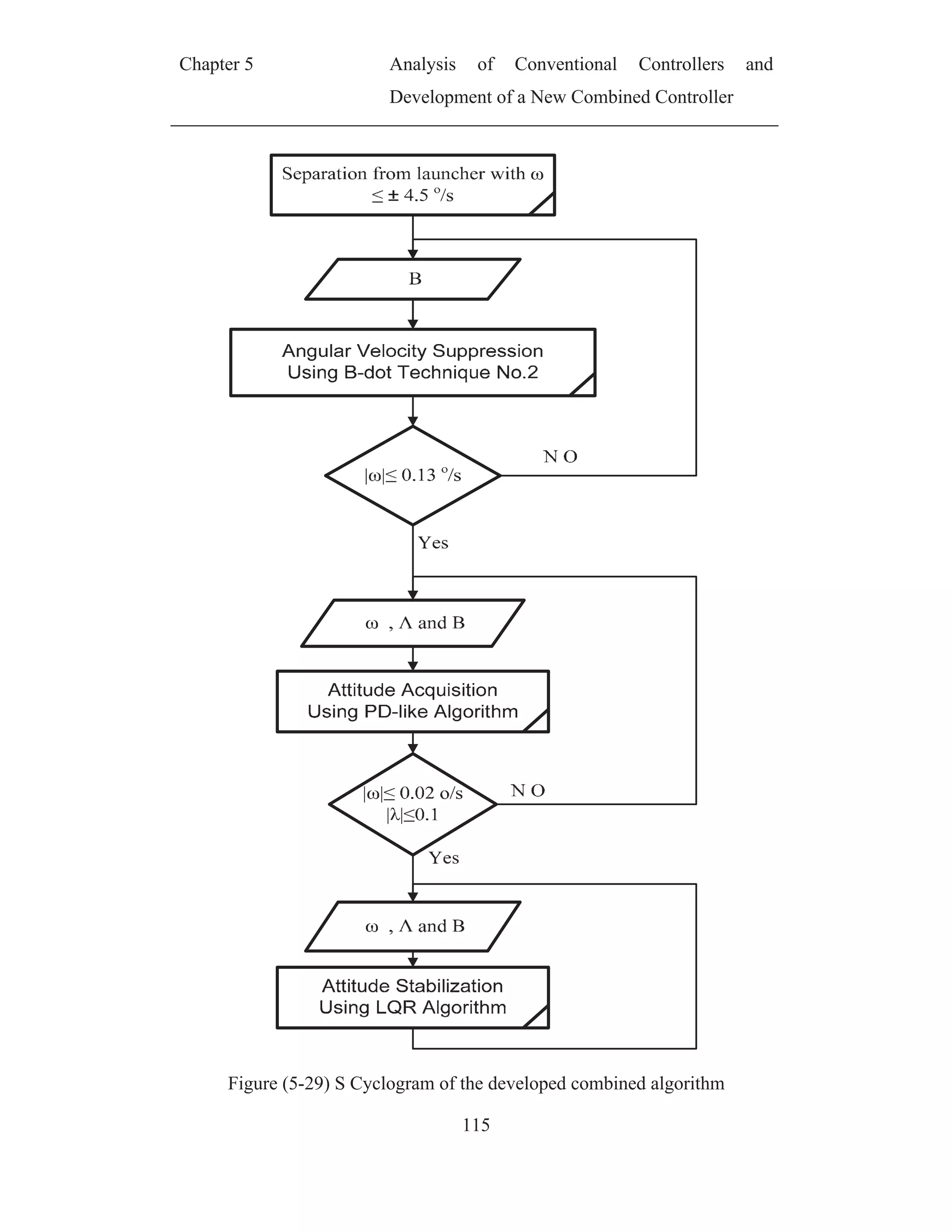
137. Ch
Fig
using ang
using com
hapter 5
gure (5-32
gular veloc
mbined alg
The ab
Table 5
2) Require
city feedba
orithm
ove simula
5-4 the com
Comparis
aT
acL
totL
T
ssE
ssE
Analy
Devel
d dipole m
ack, follow
ation result
mbined alg
son Parame
acqT [s]
cq [Am2
]
[Am2
/s]
calT [s]
s [deg.]
[deg./s]
ysis of
lopment of
118
moment du
wed by, at
ts could be
orithms res
eter
Conventio
f a New Co
uring angu
ttitude acq
e surmised
sults
Va
5,8
4.44
4.4
4.99e-6 /
±
±0.0
onal Con
ombined Co
ular veloci
quisition an
in the follo
alue
807
43e4
49e4
/ 3.539e-3
±3
0075
ntrollers a
ontroller
ity suppres
nd stabiliz
owing table
and
ssion
ation
e.

138. Chapter 6 Conclusion and Future
Work
119
CHAPTER (6)
CONCLUSION AND FUTURE WORK
Commonly used controllers for magnetic attitude control of satellite, had
been studded and compared in this thesis. The comparison was done during
done during angular velocity suppression, attitude acquisition and attitude
stabilization. The simulation results showed that. Angular velocity suppression
done by B-dot technique which depends on the deference between two
successive readings from magnetometer divided by period between the two
readings is optimum algorithm. Also, during attitude acquisition simulation
results showed that PD-like algorithm is good choice. Finally LQR algorithm
was very suitable to keep stabilization of satellite at nadir pointing.
Based on the simulation results a combined algorithm was developed in
to serve all over the satellite modes by switching between the suitable
controllers depending on the satellite stats , the simulation results showed the
effectiveness of using the developed algorithm in transient and stead stat of
satellite attitude beside saving the overall consumed power.
Future work
The following topics are not covered in this work but it is believed that
future investigation could be beneficial
Design of the magnetic attitude control based on robust techniques
needs to be investigated. This issue is not trivial; due to the system is

139. Chapter 6 Conclusion and Future
Work
120
time varying and lacking controllability in the direction of the local
geomagnetic field vector
It seems promising to design an attitude controller based on fuzzy
logic and the
Finally, attitude determination using only magnetometer and
combined it with this work will lead to design light and low power
consumption ADCS, this system can be widely used in educational
satellite such as cube-satellite.

140. Appendix A Attitude Representation
121
Appendix A
ATTITUDE REPRESENTATION
A.1. Introduction
The purpose of this appendix is to provide a short description of various
aspects of attitude transformation in space. The attitude of a three-dimensional
body is most conveniently defined with a set of axes fixed to the body. This set
of axes is generally a triad of orthogonal coordinates, and is normally called a
body coordinate frame. The attitude of a body is thought as a coordinate
transformation that transforms a defined set of reference coordinates into the
body coordinates of the satellite.
This appendix presents some basic attitude transformation techniques;
the treatment is not extensive, but rather a summary of the material required in
the main chapters of the text. For further reading on the subject, see Sabroff et
al. (1965) or Wertz (1978)
A.2. Euler angles
The rotation matrix in Euler angles of the roll pitch yaw type expresses unity
rotations around the existing axis. The rotation from frame O to frame B can be
expressed as a rotation degrees about the z-axis, followed by a rotation
degrees about the new y-axis and finally a rotation degrees about the even
newer x-axis. This rotation is shown in Figure (), and can be expressed as

141. Appendix A Attitude Representation
122
Figure (A.1) Euler angles
,,, XYZ
O
B RRRR
(A.1)
Where ,ZR , ,YR and ,XR are the unity rotations
The elements s and c have been used as an abbreviation for the
trigonometric expressions sin(·) and cos(·), respectively, to make the rotation
matrices more perspicuous. And so, the rotation matrix O
BR in (A.1)Error!
Reference source not found. can be written
ccscs
sccssccssscs
sscsccsssccc
RO
B (A.3)
If all angles are equated to zero, = = = 0, then the rotation matrix
becomes the unity matrix, 1O
BR , which implies that no rotation has occurred.
A.3. Quaternion
cs
scR
cs
sc
Rcs
sc
R XYZ
0
0
001
,
0
010
0
,
100
0
0
,,,
(A.2)
XB
X1
ZB
Y1
YB Y1
X1
X2
Z2
ZB Z2
ZO
X2
Y1
YO

142. Appendix A Attitude Representation
123
Quaternion is one of many ways to represent attitude. The quaternion
has the advantage of being without singularities for all attitudes.
A quaternion q is defined by its four vector elements 0 q1, 1 q2, 2 q3
and 3 q4, as
3
2
1
0
3210 kji
(A.4)
where ji, i, j and k k are hyper imaginary numbers satisfying
1222
kji (A.5)
kjiij (A.6)
ikjjk (A.7)
jikki (A.8)
The four parameters of a quaternion are subject to the constraint that
1
2
3
2
2
2
1
2
0 (A.9)
Which means that the quaternion has three degrees of freedom,
corresponding to the minimum set of parameters needed for attitude
representation [Wertz, 1978].
The 1st
element 0 of the quaternion is named the scalar element, and
the 2nd
,3rd
and 4th
are the complex elements. The complex part of the
quaternion is written , hence a quaternion may be written
0
(A.10)
A rotation around a unit vectoru , is represented by the quaternion
2
sin
2
cos
u
(A.11)
The complex conjugate of the quaternion is defined as

143. Appendix A Attitude Representation
124
0
3210 kji (A.12)
Note that
0
0
0
1
(A.13)
Which is the unit quaternion representing the zero rotation, i.e. no rotation.The
transposed of quaternion equals the complex conjugate of the quaternion.
The product of two quaternion , is defined in matrix form as
3
2
1
0
0123
1032
2301
3210
(A.14)
0000
T
(A.15)
Where a quaternion multiplication
Note that the multiplication of quaternion is not commutative, which is
also the case for attitude matrices.
Representing the attitude of by the attitude matrix )(R the rotation
sequence of equation (A.14), can be written in terms of the associated attitude
matrices, as
)()()( RRR (A.16)
Where )(R is given by
22
22
22
)(
2
3
2
2
2
1
2
001320231
0132
2
3
2
2
2
1
2
00321
02310321
2
3
2
2
2
1
2
0
R (A.17)
Therefore, quaternions provide simple methods for calculation of
successive rotations. So if the quaternion reflecting the rotation between frame
O and frame B is and it is required to find the projection of vector OM that
is defined in frame O in the new frame B then the following formula is used

144. Appendix A Attitude Representation
125
OOO
O
MMM
M
22
M
0
B
(A.18)
Note that the above formula for calculating BM gives the same results as
if the transformation matrixes defined in (A.15) as follows
OMR )(MB (A.19)
A.4. Direction Cosine Matrix
The basic three-axis attitude transformation is based on the direction
cosine matrix. Any attitude transformation in space is actually converted to this
essential form. In Figure ), the axes 1, 2, and 3 are unit vectors defining an
orthogonal, right-handed triad. This triad is chosen as the reference inertial
frame. Next, a similar orthogonal triad is attached to the center of mass of a
moving body, denned by the unit vectors u, v, and w,
Figure (A.2) Definition of the orientation of the satellite axes u.v.w in the
reference frame
In the context of Figure (A.2.1), we define the matrix [R] as follows:
321
321
321
][
www
vvv
uuu
R (A.20)
In this matrix, u1, u2, u3 are the components of the unit vector u along the
three axes 1,2, 3 of the reference orthogonal system: u=[u1 u2 u3]T
. In a similar
way, v and w have components v1, v2, v3 and w1, w2, w3 along the same
reference axes: v = [v1 v2 v3]T
and w = [w1 w2 w3]T
. The direction cosine matrix
[R], also called the attitude matrix, has the important property of mapping

145. Appendix A Attitude Representation
126
vectors from the reference frame to the body frame. Suppose that a vector a
has components, in the reference frame: a = [a1 a2 a3]T
. The following matrix
vector multiplication In this matrix, u1, u2, u3 are the components of the unit
vector u along the three axes 1,2, 3 of the reference orthogonal system: u=[u1 u2
u3]T
. In a similar way, v and w have components v1, v2, v3 and w1, w2, w3 along
the same reference axes: v = [v1 v2 v3]T
and w = [w1 w2 w3]T
. The direction
cosine matrix [R], also called the attitude matrix, has the important property of
mapping vectors from the reference frame to the body frame. Suppose that a
vector a has components, in the reference frame: a = [a1 a2 a3]T
. The
following matrix vector multiplication.
w
v
u
B
a
a
a
a
a
a
www
vvv
uuu
aRa
3
2
1
321
321
321
][ (A.21)
Where Ba is the vector a mapped into the body frame.
Since u is a unit vector, it follows that the scalar product ua is the
component ua of the vector a along the unit vectoru . By the same reasoning,
the components of the vector a on the remaining unit vectors of the body triad
are va and wa
Some basic properties of the matrix [R] may be stated as follows.
Each of its elements is the cosine of the angle between a body unit vector and a
reference axis; its name is derived from this property.
1. Each of the vectors u, v, w are vectors with unit length; hence:
,1,1,1
3
1
2
3
1
2
3
1
2
i
i
i
i
i
i wvu (A.22)
The unit vectors ,,, wvu are orthogonal to each other; hence
,0,0,0
3
1
3
1
3
1 i
ii
i
ii
i
ii wvwuvu (A.23)
The relationships in (2) and (3) lead to the useful identity 1T
RR , or
1
RR T
. of course, transposition of a matrix is a much simpler process than inversion
of the same matrix.

146. Appendix A Attitude Representation
127
It is well known that )(det wvuR since wvu ,, form a cubic orthogonal triad, it
follows that 1]det[R . Thus
B
T
aRa
(A.24)

147. Appendix B Transformation Matrices
Between Reference Frames
128
Appendix B
TRANSFORMATION MATRICES BETWEEN
REFERENCE FRAMES
Frame transformations are done through the identification of angles of
rotation between frames and the proper application of trigonometric functions
to those angles. The end result is arranged into a 3x3 matrix of sines and
cosines that can take a vector expressed in one coordinate frame and transform
it into another. The following four sections define the angles of rotation to be
used for each transformation and derive the corresponding transformation
matrix. Though each matrix is derived for transforming a certain direction, the
reverse direction’s matrix is obtained by simply taking the transpose of the
original transformation matrix.
B.1. OCS to ICS
Figure ) shows the angles of rotation between the OCS and GCS frames.
Knowing these angles, the transformation matrix can be shown to be:
OCS
I
OICS
OCSICS
xRx
x
icisWvcisWvs
ciscicWvcsWvscicWvssWvc
sissicWvccWvssicWvscWvc
x
)()().()().(
)().()().().()()()().().()()(
)().()().().()()()().().()()( (B.1)
Where
is the right ascension of the ascending node (RAAN) ,
i is the orbit inclination,
W is the argument of perigee

148. Appendix B Transformation Matrices
Between Reference Frames
129
is the true anomaly
I
OR is the transformation matrix from OCS to ICS
ICSx is the vector defined in ICS
OCSx is the vector defined in OCS
Note that sine and cosine functions have been abbreviated as s( ) and c( ),
respectively.
Figure (B-1) OCS with respect to ICS
B.2. GCS to ICS
The angle between the line of Aries and Greenwich line relates the
ICS frame to the GCS frame . This angle can be split into the sum of two
angles. The first angle 0 is the angle between the vernal equinox and

149. Appendix B Transformation Matrices
Between Reference Frames
130
Greenwich line at midnight. This angle can be found using the equation from
the Astronomical Almanac.
0
(B.2)
362
0 102.60193104.0812866.864018454841.24110 UUU TTT
Where
36525
0.2451545JD
TU
(B.3)
Where JD is Julian date at which UT is calculated.
The second angle is the product of the time since midnight t and the
angular rotational rate of the Earth e as follow.
te (B.4)
Using these angles the transformation can be written as:
GCS
I
GICS
GCSICS
xRx
xx
.
100
0)cos()sin(
0)sin()cos( (B.5)
Where
.I
GR is the transformation matrix from GCS to ICS
GCSx is the vector defined in GCS
ICSx is the vector defined in ICS
B.3. OCS to BCS
This transformation matrix can easily calculated by knowing the
orientation of BCS with respect to OCS in other words the orientation of
satellite with respect to orbital reference frame. The calculation of the
transformation matrix is different according to the method of attitude
representation discussed in appendix A

150. Appendix B Transformation Matrices
Between Reference Frames
131
So if the rotation between frame OCS and frame BCS is known and it is
required to find the projection of vector OCSX that is defined in frame OCS in
the new frame BCS then the following formula are used
OCS
B
BCS xRx O
(B.6)
Where R is the transformation matrix from OCS to BCS is defined as
follows
1. Equation (A.3) in case if the attitude is represented in Euler angles
2. Equation (A.19) in case if the attitude is represented in quaternions
3. Equation (A.21) in case if the attitude is represented in direction cosine
matrix

151. Reference
132
References
[1]http://ocw.mit.edu/NR/rdonlyres/Aeronautics-and-Astronautics/16-892JFall-
2004/5E921686-B4CD-4949-A0D3-9A2DD6E4D6C/0/01010
wk1_framing.pdf
[2] http://integral.esa.int/Publications/taormina_final_short2.PDF
[3]Anil K. Maini and Varsha Agrawal "Satellite technology principals and
applications" John Wiley & Sons Ltd Publishers 2007
[4] Wertz, James R. and Wiley J. Larson (eds.) “Space Mission Analysis and
Design, 3rd Ed.” Microcosm Press/Kluwer Academic Publishers 1999
[5] http://www.williamcraigcook.com/satellite/anatomy.html.
[6] Prof. R. H. "Tolson Space Flight Mechanicsa.k.a. Astrodynamics" , fall
2005 ,NC stat university , USA
[7]William E. Wieles "satellite dynamics, 2nd Ed" McGraw-Hill companies
Inc.1997
[8] http://www.inetdaemon.com/tutorials/telecom/satellite/orbits.shtml
[9] http://en.wikipedia.org/wiki/Medium_Earth_Orbit
[10] John S. Eterno, Robert O. Zermuehlen, Harold F Zimbelman. “Attitude
Determination and Control.” SPACE MISSION ANALYSIS AND DESIGN.
edited by Wiley J. Larson and James R. Wertz, second edition, Space
Technology Series, Microcosm, Inc. & Kluwer Academic Publishers, 1992,
pp. 340-366.
[11] Challa, M., Natanson, G., Deutschmann,J., and Galal, K., “A PC-Based
Magnetometer-Only Attitude and Rate Determination System for Gyroless
Satellite”, presented at the GSFC FDD Flight Mechanics. Estimation Theory
Symposium 1995. Paper No. 07, NASA Goddard Space Flight Center,
Greenbelt, Maryland, May 16-18, , pp.83-96, 1995

152. Reference
133
[12] Marcel J. Sidi. "Satellite Dynamics and Control, A Practical Engineering
Approach ".Cambridge Aerospace Series. Cambridge University Press,
Cambridge, 1997.
[13] Goldstein.H. ,classical mechanics reading , MA : Addison-Wesley , 1964
[14] Thomson .W.T, introduction to space dynamics , New York , Dover, 1986
[15] J ames R. Wertz, editor. "Satellite Attitude Determination and Control."
Kluwer Academic Publishers, Dordrecht, 2000.
[16] D. Lebedev, A. Tkachenko ” Magnetic Attitude Control System for Low-
Earth”, Multibody System Dynamics,2001.
[17]Beletsky, V.V., “Libration of a Satellite”, Transactions: Artificial Satellites
of the Earth, Moscow, USSR Academy of Sciences, Issue 3, 1959
[18] Wisniewski, R., & Blanke, M. (1999). Fully magnetic attitude control for
satellite subject to gravity gradient. Automatica, 35(7), p.1201–1214.
[19]Jan Tomy,”magnetic attitude control for satellites” , 43rd
IEEE Conference
on Decision and Control 2004, Atlantis, Paradise Island, Bahamas
[20] Wisniewski, R. "Satellite Attitude Control Using Only Electromagnetic
Actuation", Ph.D.Thesis, Aalborg University, Denmark, 1996
[21] Enrico Silani, Marco Lovera " Magnetic satellite attitude control: a survey
and some new results", Control Engineering Practice,2003
[22] Carlo Arduini and Paolo Baiocco. "Active Magnetic Damping Attitude
Control for Gravity Gradient Stabilized Spacecraft". Journal of Guidance
Control and Dynamics, 1997.
[23] Daniel Vernon Guerrant” Design And Analysis of Fully Magnetic Control
For Picosatellite Stabilization” Master thesis , California Polytechnic State
University,2005
[24] Marco Lovera and Alessandro Astolfi “Global magnetic attitude control
of satellite”, 43rd
IEEE Conference on Decision and Control 2004, Atlantis,
Paradise Island, Bahamas

153. Reference
134
[25] Kjell Magne Fauske” Ncube Attitude Control”, Department of
Engineering Cybernetics,NTNU, 2002
[26] Saiijay P. Bhat & Ajit S. Dhain “Controllability of Satellite Attitude
Under Magnetic Actuation “ Proceedings of the 42nd IEEE , Conference on
Decision and Control Maui, Haraii USA, 2003
[27]Kristiansen, R.” Attitude controll of mini satellite”. Master’s thesis, NTNU
,2000
[28] Jens Gießelmann "Development of an Active Magnetic Attitude
Determination and Control System for Picosatellites on highly inclined
circular Low Earth Orbits" Master thesis , School of Aerospace, Mechanical
and Manufacturing Engineering Science, Engineering and Technology
Portfolio , RMIT University, Germany, 2006