The document discusses four sorting algorithms: selection sort, bubble sort, insertion sort, and merge sort. It provides pseudocode for the selection sort algorithm and describes how it works by making successive passes through an array and swapping elements until the array is fully sorted. Bubble sort and insertion sort are also described as making multiple passes through an array, comparing and swapping adjacent elements until the array is in order. Pseudocode is provided for the bubble sort and insertion sort algorithms.

1. Sorting
Sorting is any process of arranging items
systematically.
ascending :A to Z, 0 to 9
descending order: Z to A, 9 to 0
For dates and times, ascending means that earlier values
precede later ones e.g. 1/1/2000 will sort ahead of
1/1/2001

2. Sorting
Four algorithms are described
1. Selection sort
2. Bubble sort
3. Insertion Sort
4. Merge Sort (Assignment)

3. Selection Sort
 In the first pass, each item in the list is
compared with the first item in the list
 If the first item in the list is bigger then the
item being compared then they are swapped.

4. Selection Sort
7 5 9 6 1 8 2 0 3 4
1st Comparison
Swap

5. Selection Sort
5 7 9 6 1 8 2 0 3 4

6. Selection Sort
5 7 9 6 1 8 2 0 3 4
2nd Comparison

7. Selection Sort
5 7 9 6 1 8 2 0 3 4
3rd Comparison

8. Selection Sort
5 7 9 6 1 8 2 0 3 4
4th Comparison
Swap

9. Selection Sort
1 7 9 6 5 8 2 0 3 4
5th Comparison

10. Selection Sort
1 7 9 6 5 8 2 0 3 4
6th Comparison

11. Selection Sort
1 7 9 6 5 8 2 0 3 4
7th Comparison
Swap

12. Selection Sort
0 7 9 6 5 8 2 1 3 4

13. Selection Sort
0 7 9 6 5 8 2 1 3 4
8th Comparison

14. Selection Sort
0 7 9 6 5 8 2 1 3 4
9th Comparison

15. Selection Sort
0 7 9 6 5 8 2 1 3 4
1st
Comparison

16. Selection Sort
0 7 9 6 5 8 2 1 3 4
2nd Comparison
Swap

17. Selection Sort
0 6 9 7 5 8 2 1 3 4

18. Selection Sort
0 6 9 7 5 8 2 1 3 4
3rd Comparison
Swap

19. Selection Sort
0 5 9 7 6 8 2 1 3 4

20. Selection Sort
0 5 9 7 6 8 2 1 3 4
4th Comparison

21. Selection Sort
0 5 9 7 6 8 2 1 3 4
5th Comparison
Swap

22. Selection Sort
0 2 9 7 6 8 5 1 3 4

23. Selection Sort
0 2 9 7 6 8 5 1 3 4
And so on…

24. Selection Sort
until…
0 1 2 3 4 5 6 7 8 9

25. Selection Sort
Must make N-1 passes through list even when
fully sorted or partially sorted

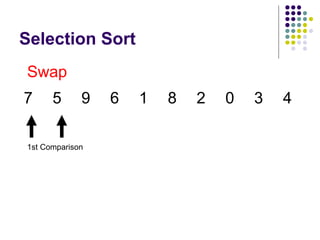
26. Selection Sort Algorithm
Step 1. [Starting Selection Loop]
Repeat step 2 For S=1 to N-1 by 1
Step 2. [Starting Selection Loop]
Repeat step 3 For C=S+1 to N by 1
Step 3. [Compare Element]
If(A[s]> A[c]) Then
Temp=A[S]
A[S]=A[C]
A[S]=Temp
Exit

27. Bubble Sort
 Bubble sort is a simple algorithm that
repeatedly steps through the list, compares
adjacent pairs and swap them if they are in
wrong order. The pass through the list is
repeated until list is sorted.

28. Bubble sort Example
7 5 9 6 1 8 2 0 3 4
First Comparison
Swap

29. Bubble sort
5 7 9 6 1 8 2 0 3 4

30. Bubble sort
5 7 9 6 1 8 2 0 3 4
Second Comparison

31. Bubble sort
5 7 9 6 1 8 2 0 3 4
Third Comparison
Swap

32. Bubble sort
5 7 6 9 1 8 2 0 3 4

33. Bubble sort
5 7 6 9 1 8 2 0 3 4
Fourth Comparison
Swap

34. Bubble sort
5 7 6 1 9 8 2 0 3 4

35. Bubble sort
5 7 6 1 9 8 2 0 3 4
Fifth Comparison
Swap

36. Bubble sort
5 7 6 1 8 9 2 0 3 4

37. Bubble sort
5 7 6 1 8 9 2 0 3 4
Sixth Comparison
Swap

38. Bubble sort
5 7 6 1 8 2 9 0 3 4

39. Bubble sort
5 7 6 1 8 2 9 0 3 4
Seventh Comparison
Swap

40. Bubble sort
5 7 6 1 8 2 0 9 3 4

41. Bubble sort
5 7 6 1 8 2 0 9 3 4
8th Comparison
Swap

42. Bubble sort
5 7 6 1 8 2 0 3 9 4

43. Bubble sort
5 7 6 1 8 2 0 3 9 4
9th Comparison
Swap

44. Bubble sort
5 7 6 1 8 2 0 3 4 9
Notice… we are sorting list into an ascending list. The largest number is now
at the end of the list…where it should be!
This completes the first pass through the list.

45. Bubble sort
5 7 6 1 8 2 0 3 4 9
The process begins again.
1st Comparison Second Pass

46. Bubble sort
5 7 6 1 8 2 0 3 4 9
2nd Comparison
Swap
Second Pass

47. Bubble sort
5 6 7 1 8 2 0 3 4 9
Second Pass

48. Bubble sort
5 6 7 1 8 2 0 3 4 9
3rd
Comparison
Swap
Second Pass

49. Bubble sort
5 6 1 7 8 2 0 3 4 9
Second Pass

50. Bubble sort
5 6 1 7 8 2 0 3 4 9
4th Comparison Second Pass

51. Bubble sort
5 6 1 7 8 2 0 3 4 9
5th Comparison
Swap
Second Pass

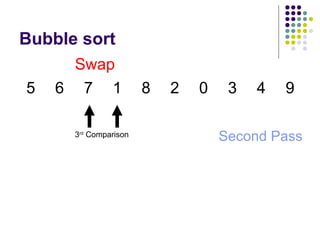
52. Bubble Sort
Write an algorithm to sort an array A consisting of
N elements in ascending order using bubble sort
Suppose variable U represents the control variable
for upper loop to control the number of iteration .
Similarly , variable I represent the control variable
for inner loop that scans the array starting from
element A[1] to A[U]

53. Cont.……
1. Set U=N
2. [Upper loop]
Repeat step 3 to 7 while (U>=1)
3. Set I=1
4. [Inner Loop]
Repeat step 5 to 6 while (I<=U)
5. IF A[I]>A[I+1]
T=A[I]
A[I]=A[I+1]
A[I+1]=T END IF
6. I=I+1
7. U=U-1
8. EXIT

54. Insertion Sort
 In insertion sort algorithm, compare the value
until all the previous value is lesser than
compared value. Insertion sort is more
efficient than bubble sort because in insertion
sort the elements comparisons are lesser as
compared to bubble sort. Insertion sort is
suitable for small data.

55. Insertion Sort Example

56. Algorithm for insertion sort
Write an algorithm to sort an array A
consisting of N elements in ascending order
using Insertion sort method
Suppose variable U represents the control
variable for upper loop to control the number
of iteration . Similarly , variable I represent
the control variable for inner loop that scans
the array starting from element A[1] to A[U]

57. CONT.….
1. REPEAT STEP 2 TO 6 FOR C=1 TO N
2. TEMP=A[C]
3. L=C
4. REPEAT STEP 3 to 7 WHILE (L>0 AND TEMP<A[L-1])
5. A[L]=A[L-1] [END OF STEP 4 INNER LOOP]
6. A[L]=TEMP [INSERT VALUE]
[END OF STEP 1 UPPER LOOP]
7. EXIT