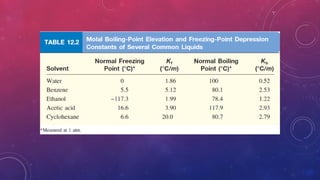
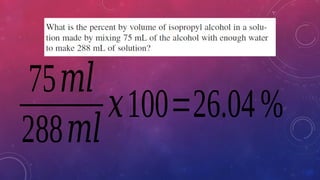The document discusses solutions, their types, and concentrations, defining terms such as solute, solvent, concentrated, and dilute solutions. It elaborates on methods to express concentration, including percent concentration, molarity, molality, and normality, along with examples for clarity. Additionally, it covers colligative properties like vapor pressure lowering and boiling point elevation, and provides relevant formulas and calculations.

1. SOLUTION AND CONCENTRATIONS
JEMIMAH JOY I. GUARIN

2. SOLUTIONS
What are solutions?
• Homogeneous mixtures that contain solute
and solvent.
• Substance that dissolves in a solvent 
soluble
• Substance that does not dissolve in a solvent
 insoluble
• Two liquids that are soluble in each other 
miscible
• Liquids that are not soluble in each other 
immiscible
CONCENTRATION
Is a measure of the amount of solute
dissolved in a given amount of solvent or
solution.
Concentrated solution  contains a large
amount of solute.
Dilute solution  contains a small amount of
solute.

3. PERCENT CONCENTRATION
 % weight is often used to express the concentration of commercial aqueous reagents.
 % volume is commonly used to specify the concentration of a solution prepared by
diluting a pure liquid compound with another liquid.
 % weight /volume is often used to indicate the composition of dilute aqueous solutions
of solid reagents.

4. Example/s:

6. 75𝑚𝑙
288𝑚𝑙
𝑥100=26.04%

7. A limestone sample weighing 1.267 g and containing 0.3684
g Iron. Calculate for % Fe in the solution.

8. EXAMPLE/S:
70% (w/w) Nitric acid solution
 the reagent contains 70 g HNO3 per 100 g solution.
5% (v/v) aqueous solution of methanol
 a solution is prepared by diluting 5.0 ml of pure
methanol with enough water to give 100 ml.
5% (w/v) aqueous silver nitrate
 it is prepared by dissolving 5 g of AgNO3 in sufficient
water to give 100 ml of solution.

9. Molarity (M)
• The number of moles of solute in 1L of solution.
• Most widely used.

10. Example/s:

11. Molar mass LiI = 133.8 g/mol

12. Molar mass CaCl2 = 111.1 g/mol

13. Molality (m)
• Temperature-dependent concentration
• is the number of moles of solute dissolved in 1 kg (1000 g) of solvent.
• The unit is: mol/kg

14. Example/s:

16. Normality (N)
• Is defined as gram-equivalent of solute dissolved in 1 liter of the solution.
• Also called as equivalent concentration.
• EQUIVALENT WEIGHT = number of Hydrogen ions for acids ;
number of hydroxide ions
for bases
N = M x n
Where:
M – molarity (mol/L) ; n- number of equivalents produced

17. Example/s:
Find the normality of 0.0521 M .
Given:
M= 0.0521
n= 3
N= M x n
N= (0.0521 mol/L) (3 eq/mol)
N= 0.156 eq/L
or 0.156 N

18. • Calculate the normality of 60 g NaOH in 1L of water.
Find the molarity of the solution:
Then, proceed with the formula for normality:
N= M x n
N= (1.5 mol/L) ( 1 eq/mol)
N= 1.5 N

19. Parts per Million (ppm) and Parts per Billion (ppb)
𝐶𝑝𝑝𝑏=
𝑚𝑎𝑠𝑠𝑜𝑓 𝑠𝑜𝑙𝑢𝑡𝑒
𝑚𝑎𝑠𝑠𝑜𝑓 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛
𝑥10
9
𝑝𝑝𝑏

20. Example/s:

21. Mole Fraction (X)
• a dimensionless quantity that expresses the ratio of the number of moles of
solute or solvent to the total number of moles of solute plus solvent in a
solution.
• The mole fraction for the solvent and the mole fraction for the solute are
equal to:

22. Example:
Suppose you wish to find the mole fraction of the solvent and of the solute in a solution
that contains 215 g of water and 44.0 g of NaOH.
Determine the # of moles of solute and solvent by dividing each mass by its molar
mass.

23. DILUTING A SOLUTION
Where:
M1- initial concentration
V1- initial volume
M2- final concentration
V2- final volume

24. Example/s:

26. COLLIGATIVE PROPERTIES OF SOLUTIONS
• Colligative properties- are properties that depend only on the number of solute particles in
solution and not on the nature of the solute particles.
• Vapor-pressure lowering
• Boiling-point elevation
• Freezing-point depression
• Osmotic Pressure

27. VAPOR-PRESSURE LOWERING
• The vapor pressure of a solution containing a nonvolatile solute is lower than the vapor pressure of the
pure solvent.
• The relationship between solution vapor pressure and solvent vapor pressure depends on the
concentration of the solute in the solution.
• Raoult’s law- the vapor pressure of a solvent over a solution, , is given by the vapor pressure of the pure
solvent, , times mole fraction of the solvent in the solution, :

28. • Example:
Vapor pressure of water at 30°C = 31.82 mmHg; Assume the density of the sol’n = 1.00 g/mL.

30. • Calculate the vapor pressure of a solution made by dissolving 50.0 g glucose, C6H12O6, in 500 g of
water. The vapor pressure of pure water is 47.1 torr at 37°C.
Calculate first the mole fraction of water (solvent) in this sugar-water solution.

32. BOILING-POINT ELEVATION
• The temperature difference between the boiling point of a solution and the boiling point of its pure
solvent.
• The greater the number of solute particles in the solution, the greater is the boiling point elevation.
Where: m= molality of the solution
= molal boiling-point elevation constant (°C/m)

33. FREEZING-POINT DEPRESSION
• The temperature difference between the freezing point of a solution and the freezing point of its pure solvent.
• The freezing point of a solution is always lower than that of a pure solvent.
Where: m= molality of the solution
= molal freezing-point depression constant (°C/m)

35. Example:

36. Solution:
 Solve the molality of the solution.
-Find the number of moles of Ethylene glycol
-Convert the given mass of the solvent in kilograms

37. • Now, compute for the Tf and Tb:

38. OSMOTIC PRESSURE
• It is a pressure related to Osmosis- w/c is the diffusion of solvent particles across a semipermeable membrane
from an area of lower solute concentration to an area of a higher solute concentration.
Where:
M= molarity of solution
R= gas constant
T= absolute temperature
->Osmotic pressure is expressed in atm.

39. • Example: