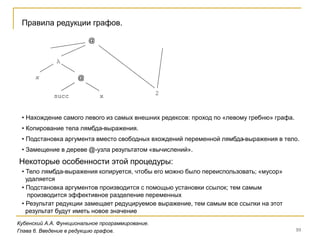
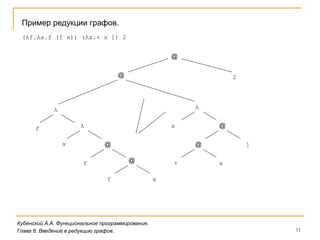
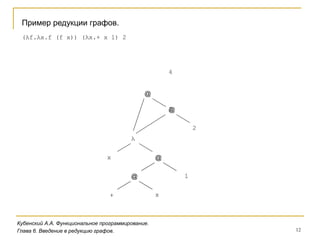
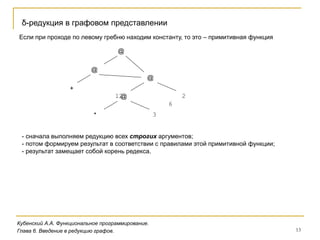
Документ рассматривает системы исполнения функциональных программ, включая представление и компиляцию императивных языков, таких как вычисление факториала. Обсуждаются способы обработки программ через интерпретацию и компиляцию, а также введение в редукцию графов для лямбда-выражений. Основное внимание уделяется структуре программ, типам выражений и правилам редукции в контексте функционального программирования.

1. 1
Кубенский А.А. Функциональное программирование.
Глава 5. Системы исполнения функциональных программ.
Глава 5. Системы исполнения функциональных программ
5.3. Функциональные модели последовательных процессов
Рассмотрим простой язык императивного программирования без функций,
переходов и сложных структур данных.
Выражения:
 Целые числа: 12 25 0
 Простые переменные целого типа: x myInt
 Унарные и бинарные операции с целыми результатами: (x+12) * (y-1)
 Логические константы и выражения (но не переменные): not (x < 5)
Операторы:
 Присваивание: x := x+1
 Последовательное исполнение: begin s1; s2; ... end
 Условный оператор: if b then s1 else s2
 Пустой оператор: skip
 Оператор цикла: while b do s
Программа начинает работу в состоянии, заданном совокупностью значений переменных
(например, заданных оператором ввода данных), а результат программы – конечное состояние
(например, выведенное в конце работы оператором вывода).

2. 2
Кубенский А.А. Функциональное программирование.
Глава 5. Системы исполнения функциональных программ.
Рассмотрим программу вычисления факториала.
Пример программы.
begin f := 1;
while n > 1 do begin
f := f * n;
n := n – 1
end
end
В начальном состоянии существенно только
значение переменной n; в конце работы результат
определяется значением переменной f.
Прежде всего, переведем программу в вид, удобный для обработки.
data Expression = { представление выражений }
data Operator = { представление операторов }
data Context = { представление контекста переменных }
Два способа обработки и исполнения программы:
 Интерпретация: interpret :: Operator -> Context -> Context
 Компиляция: compile :: Operator -> (Context -> Context)
На самом деле оба способа представлены одной и той же карринговой функцией!

3. 3
Кубенский А.А. Функциональное программирование.
Глава 5. Системы исполнения функциональных программ.
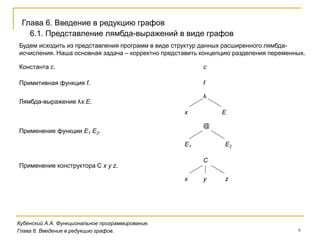
Представление выражений и программ.
data Expression = Integral Int | Logical Bool
| Variable String
| Unary String Expression
| Binary Expression String Expression
data Operator = Skip
| Assignment String Expression
| Sequence [Operator]
| If Expression Operator Operator
| While Expression Operator
type Context = [(String, Expression)]
interpret :: Operator -> Context -> Context
eval :: Expression -> Context -> Expression
eval v@(Integral n) _ = v
eval v@(Logical b) _ = v
eval (Variable x) ctx = assoc x ctx
eval (Unary op ex) ctx = intrinsic op [eval ex ctx]
eval (Binary e1 op e2) ctx = intrinsic op [eval e1 ctx, eval e2 ctx]
intrinsic "+" [(Integral a), (Integral b)] = Integral (a+b)
intrinsic "-" [(Integral a)] = Integral (-a)
intrinsic "and" [(Logical a), (Logical b)] = Logical (a && b)
intrinsic :: String -> [Expression] -> Expression

4. 4
Кубенский А.А. Функциональное программирование.
Глава 5. Системы исполнения функциональных программ.
Исполнение операторов.
replace :: String -> Expression -> Context -> Context
replace x val = map ((y,v) -> (y,if x == y then val else v))
replace "f" (Integral 20) [("n", (Integral 4)), ("f", (Integral 5))]
Например:
даст в результате [("n", (Integral 4)), ("f", (Integral 20))]
interpret :: Operator -> Context -> Context
interpret Skip ctx = ctx
interpret (Assignment x expr) ctx = replace x (eval expr ctx) ctx
interpret (Sequence []) ctx = ctx
interpret (Sequence (s:seq)) ctx = interpret (Sequence seq) (interpret s ctx)
interpret (If expr s1 s2) ctx = case (eval expr ctx) of
(Logical True) -> interpret s1 ctx
(Logical False) -> interpret s2 ctx
interpret oper@(While expr s) ctx = case (eval expr ctx) of
(Logical True) -> interpret oper (interpret s ctx)
(Logical False) -> ctx

5. 5
Кубенский А.А. Функциональное программирование.
Глава 5. Системы исполнения функциональных программ.
Пример компиляции и исполнения программы
begin f := 1;
while n > 1 do begin
f := f * n;
n := n – 1
end
end
program =
Sequence
[(Assignment "f" (Integral 1)),
(While
(Binary (Variable "n") ">" (Integral 1))
(Sequence
[(Assignment "f" (Binary (Variable "f") "*" (Variable "n"))),
(Assignment "n" (Binary (Variable "n") "-" (Integral 1)))]))
]
compile program - функция преобразования контекстов
interpret program [("f", (Integral 0)), ("n", (Integral 3))]
[("f", (Integral 6)), ("n", (Integral 0))]

6. 6
Кубенский А.А. Функциональное программирование.
Глава 6. Введение в редукцию графов.
Глава 6. Введение в редукцию графов
6.1. Представление лямбда-выражений в виде графов
Будем исходить из представления программ в виде структур данных расширенного лямбда-
исчисления. Наша основная задача – корректно представить концепцию разделения переменных.
Константа c. c
Примитивная функция f. f
Лямбда-выражение λx.E.
λ
x E
Применение функции E1 E2.
@
E1 E2
Применение конструктора C x y z.
C
x zy

7. 7
Кубенский А.А. Функциональное программирование.
Особенности представления некоторых типов выражений.
Представление лямбда-выражений в виде графов (продолжение).
Глава 6. Введение в редукцию графов.
Частичное применений примитивных функций и конструкторов.
1+2 + 1 2 + 1
@
+ 1
@
2
@
+ 1
1 : lst : 1 lst
:
1 lst
: 1
@
: 1
или :
1 t
λ
t

8. 8
Кубенский А.А. Функциональное программирование.
Представление лямбда-выражений в виде графов (продолжение).
Глава 6. Введение в редукцию графов.
Блоки let x = E1 in E2 и letrec x1 = E1;... xk = Ek in E.
let x = E1 in E2 (λx.E2) E1
E2
λ
x
@
E1
letrec x1 = E1;... xk = Ek in E – моделируется с помощью циклических графов.

9. 9
Кубенский А.А. Функциональное программирование.
let twice = λf.λx.f (f x) in twice (λx.+ x 1) 2
Пример представления выражения в виде графа.
Глава 6. Введение в редукцию графов.
(λf.λx.f (f x)) (λx.+ x 1) 2
2
λ
x
λ
f
f
@
x
@
f
λ
@
@
x @
@
+ x
1

10. 10
Кубенский А.А. Функциональное программирование.
• Нахождение самого левого из самых внешних редексов: проход по «левому гребню» графа.
Правила редукции графов.
Глава 6. Введение в редукцию графов.
2
x
x
@
succ
λ
@
• Копирование тела лямбда-выражения.
x
@
succ
• Подстановка аргумента вместо свободных вхождений переменной лямбда-выражения в тело.
• Замещение в дереве @-узла результатом «вычислений».
Некоторые особенности этой процедуры:
• Тело лямбда-выражения копируется, чтобы его можно было переиспользовать; «мусор»
удаляется
• Подстановка аргументов производится с помощью установки ссылок; тем самым
производится эффективное разделение переменных
• Результат редукции замещает редуцируемое выражение, тем самым все ссылки на этот
результат будут иметь новое значение

11. 11
Кубенский А.А. Функциональное программирование.
Пример редукции графов.
Глава 6. Введение в редукцию графов.
(λf.λx.f (f x)) (λx.+ x 1) 2
2
λ
x
λ
f
f
@
x
@
f
λ
@
@
x @
@
+ x
1

12. 12
Кубенский А.А. Функциональное программирование.
Глава 6. Введение в редукцию графов.
2
λ
@
@
x @
@
+ x
1
Пример редукции графов.
(λf.λx.f (f x)) (λx.+ x 1) 2
@
@
+
1
3
4

13. 13
Кубенский А.А. Функциональное программирование.
δ-редукция в графовом представлении
Глава 6. Введение в редукцию графов.
Если при проходе по левому гребню находим константу, то это – примитивная функция
2
+
@
3
@
- сначала выполняем редукцию всех строгих аргументов;
- потом формируем результат в соответствии с правилами этой примитивной функции;
- результат замещает собой корень редекса.
@
@
*
6
12

14. 14
Кубенский А.А. Функциональное программирование.
Общий алгоритм редукции графов (пока без учета рекурсии)
Глава 6. Введение в редукцию графов.
while (выражение не находится в СЗНФ) {
спуск от корня по левому гребню до первой вершины, отличной от @-вершины;
switch (тип вершины) {
case (примитивная функция):
if (число аргументов k > числа пройденных @-вершин)
выражение находится в СЗНФ;
else {
редуцировать все строгие аргументы;
сформировать результат согласно правилам примитивной функции;
заменить k-ю @-вершину этим результатом;
}
break;
case (λ-вершина):
if (выше нет @-вершин)
выражение находится в СЗНФ;
else {
создать копию тела с подстановкой (разделяемого) аргумента
вместо свободных вхождений переменной λ-выражения;
подставить результат вместо вершины редекса (первая @-вершина вверх по гребню);
}
break;
default: // константа-значение или конструктор
if (выше нет @-вершин)
выражение находится в СЗНФ;
else
ошибка типа !
break;
}
}

15. 15
Кубенский А.А. Функциональное программирование.
Использование вершин-синонимов
Глава 6. Введение в редукцию графов.
При выполнении редукций есть одна проблема, связанная с копированием: в теле функции
переменная может быть в корне. Тогда вместо подстановки ссылки на аргумент придется делать
копию вершины, представляющей аргумент.
+
@
λ
@
x
1
2
x
@
x
@
Можно вместо копирования вершины создавать «вершину-синоним» - «прозрачную» по ссылкам.
Θ
При прохождении вершины-синонима можно оптимизировать их количество, убирать двойные
синонимы, заменять ссылки на синоним ссылками на саму вершину.

16. 16
Кубенский А.А. Функциональное программирование.
Использование вершин-синонимов (продолжение)
Глава 6. Введение в редукцию графов.
Аналогичная проблема возникает при применении примитивных функций-селекторов, которые
не преобразуют, а просто выдают аргумент или его часть (например, head или tail).
head
head
@
@
:
:
1 nil
nil
head (cons (head (cons 1 nil)) nil)
Θ
Θ