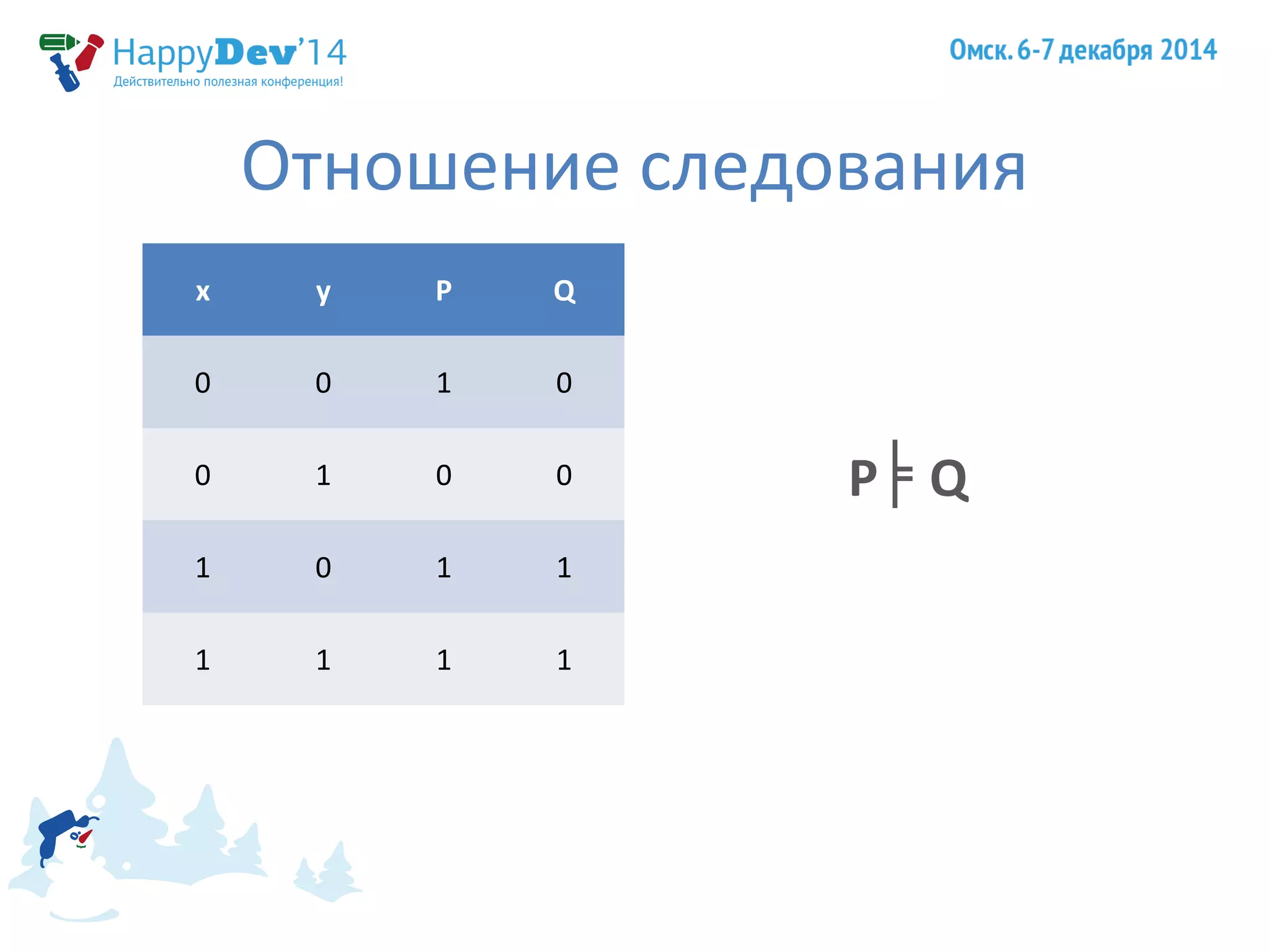
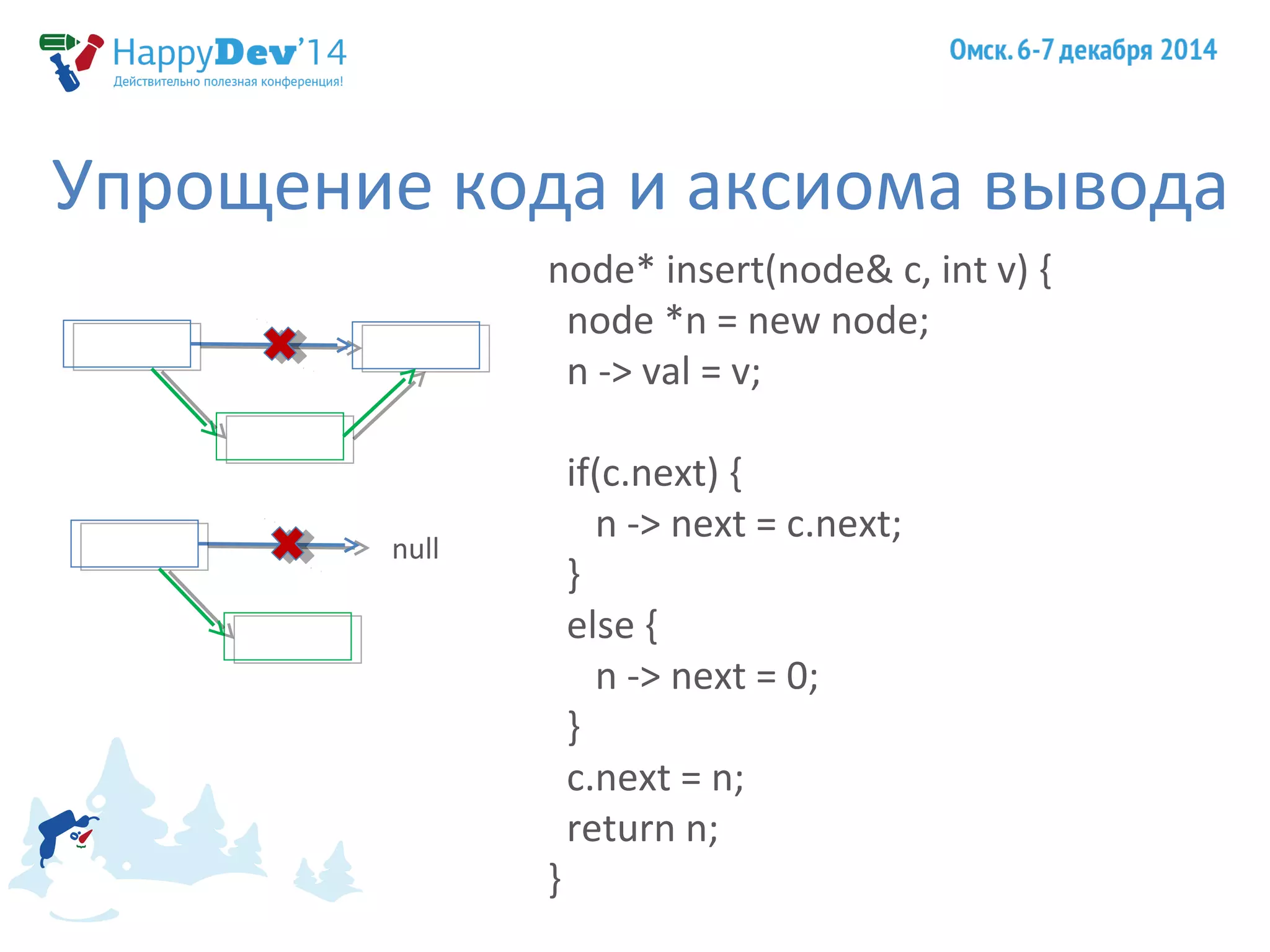
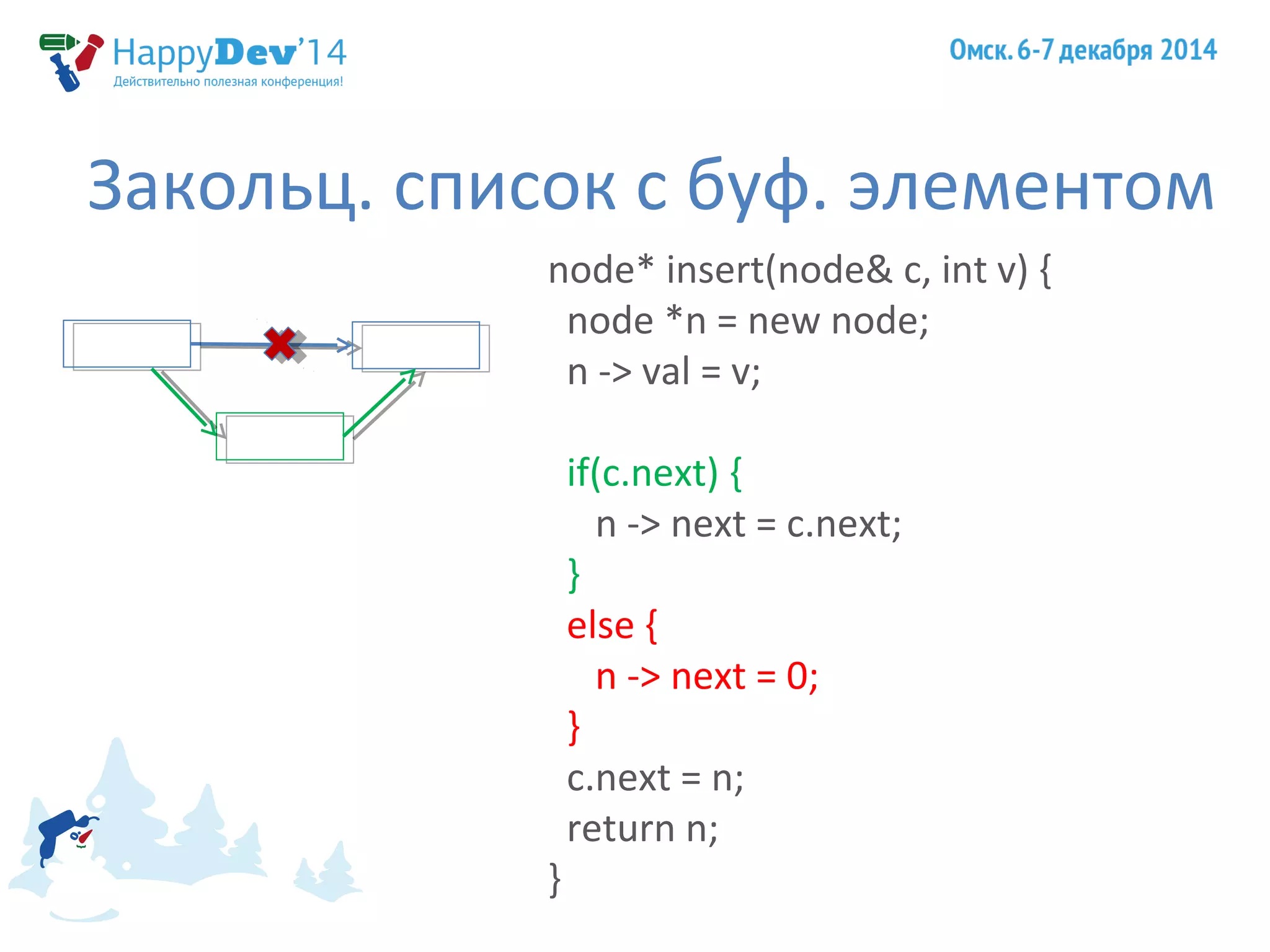
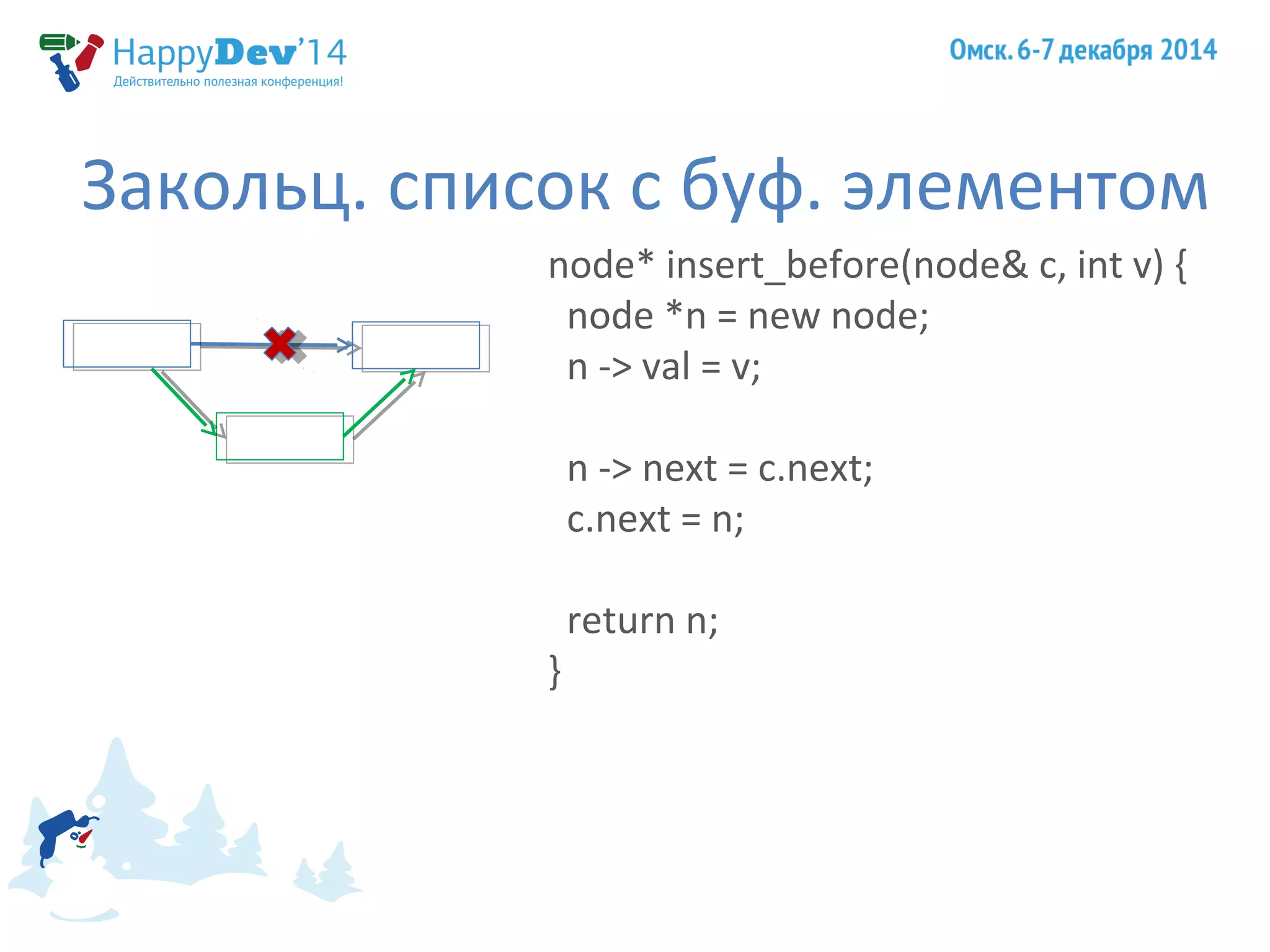
Доклад Евгения Тюменцева охватывает важные аспекты принципов программирования S.O.L.I.D., обсуждая логику, аксиомы и повторное использование кода в разработке. Он затрагивает ключевые темы, такие как контрактное программирование, аксиомы вывода, инварианты и принципы проектирования, приводя примеры для иллюстрации. Также упомянуты достижения Чарльза Хоара и его вклад в компьютерные науки.

1. Еще раз про S.O.L.I.D
Математическое обоснование или
почему Вы не можете их
игнорировать

2. Докладчик
Тюменцев Евгений
14 лет преподаю
ИМИТ, ФКН ОмГУ
ИТ-компании
Школа программиста
10 лет разрабатываю ПО
разработчик, архитектор
PM, насяльника

3. 1. Факты из логики

4. Импликация →
y y x→y
0 0 1
0 1 1
1 0 0
1 1 1

5. Интерпретация для множеств
A
B

6. Общезначимая формула
╞ P
Примеры: ╞ x V x’, ╞ P → P

7. Отношение следования
P╞ Q
x y P Q
0 0 1 0
0 1 0 0
1 0 1 1
1 1 1 1

8. Выводимость
Пусть L – множество формул, B – формула.
Тогда L ⊦ B, если ∃ B1, B2, …, Bn , что
1.Bn – это B,
2.Bi – это
либо формула из L,
либо аксиома,
либо общезначимая
формула,
либо формула полученная
при

9. Аксиомы исчисления
высказываний

10. Modus Ponens (правило вывода)

11. 2. Логика Хоара

12. Об авторе
1969 г. An Axiomatic Basis for Computer
Programming
1971 г. Procedures and Parameters: An
Axiomatic Approach
1980 г. премия Тьюринга
1990 г. Медаль “Пионер компьютерной
техники”
2000 г. рыцарский титул за заслуги в
области образования и компьютерной
техники, премия Киото
Чарльз Хоар

13. Тройка Хоара
{pred} statement {post}
Пример: {x == 42} y=x+1; {y == 43 ^ x == 42}

14. Аксиома пустого оператора
{P} skip {P}

15. Аксиома присваивания
{P[E/x]} x := E {P}
Пример: {(y+1)*3+w*(y+1+3) ==z}
x=y+1;
{ x*3+ w*(x+3)==z}

16. Аксиомы оператора цикла
{P ^ B} S {P} {P} while ╞ B do S done {B’ ^ P}

17. Аксиомы условного оператора
{B ^ P} S {Q}, {B’ ^P} T {Q} {P} ╞ if B then S else T endif {Q}
{B ^ P} S {Q}╞ {P} if B then S endif {Q}

18. Аксиомы вывода
P1 → P, {P} S {Q}, Q → Q1 ╞ {P1} S {Q1}
P1 → P, {P} S {Q} ╞ {P1} S {Q}
{P} S {Q}, Q → Q1 ╞ {P} S {Q1}

19. Аксиома вывода согласуется с
условным оператором
Пусть L = {{P} f {Q}}, B – предикат.
P^B→P (A3 исчисления
высказываний)
{P^B}f{Q} (аксиома вывода)
{P}if (B) then f endif {Q} (аксиома условного
оператора)

20. Неявные предположения
{P ^ B} с {Q}
{P} assert(B); c {Q}

21. Упрощение кода и аксиома вывода
node* insert(node& c, int v) {
node *n = new node;
n -> val = v;
if(c.next) {
n -> next = c.next;
}
else {
n -> next = 0;
}
c.next = n;
return n;
}
null

22. Как упростить операцию insert?

23. Закольц. список с буф. элементом
node* insert(node& c, int v) {
node *n = new node;
n -> val = v;
if(c.next) {
n -> next = c.next;
}
else {
n -> next = 0;
}
c.next = n;
return n;
}

24. Закольц. список с буф. элементом
node* insert_before(node& c, int v) {
node *n = new node;
n -> val = v;
n -> next = c.next;
c.next = n;
return n;
}

25. Распараллеливание алгоритмов
Lock-free алгоритмы
Ослабленные
утверждения

26. Аксиома композиции
{P} S {Q}, {Q} T {R} ╞ {P} S;T {R}

27. Контрактное программирование
• Предусловия
• Постусловия
• Инварианты

28. Модульные тесты
Arrange
Act
Assert

29. 3. S.O.L.I.D

30. Повторное использование
Повторное использование кода — методология
проектирования компьютерных и других систем,
заключающаяся в том, что система (компьютерная
программа, программный модуль) частично либо
полностью должна составляться из частей, написанных
ранее компонентов и/или частей другой системы, и
эти компоненты должны применяться более одного
раза (если не в рамках одного проекта, то хотя бы
разных).
https://ru.wikipedia.org/wiki/Повторное_использование_кода

31. А можно ли по-другому?
Выводимость прямо предписывает строить
новые тройки из предыдущих!

32. Когда происходит повторное
использование?
Если нужно внести изменение в
существующее приложение, то мы пытаемся
повторно использовать свой же собственный
код, чтобы получить тоже приложение, но с
новой функциональностью.

33. Чем грозят правки кода?
B1, B2, …, A1
B3, A1, …, A2
B5, A2, …, A3
A2, B6, …, A4
A2, A4, …, A5

34. Чем грозят правки кода?
B1, B2, …, A1
B3, A1, …, A2
B5, A2, …, A3
A2, B6, …, A4
A2, A4, …, A5

35. Матрицы
class matrix {
int size;
double *body;
public:
matrix(int s): size(s) {
body = new double[s*s];
}
void transform() {
…
}
double det() const {
…
}
};

36. Матрицы: добавляем matrix()
class matrix {
int size;
double *body;
public:
matrix(int s): size(s) {
body = new double[s*s];
}
void transform() {
…
}
double det() const {
…
}
};
class matrix {
public:
matrix(): size(0), body(0) {
}
};

37. Придется изменять методы
class matrix {
int size;
double *body;
public:
matrix(): size(0), body(0) {
}
matrix(int s): size(s) {
body = new double[s*s];
}
void transform() {
if(!body) throw exception();
…
}
double det() const {
if(!body) throw exception();
…
}
};

38. Что случилось
Инвариант класса matrix: size > 0
Конструктор matrix() нарушил инвариант: size = 0
Предусловия методов изменились с size > 0 на size ≥ 0, но
{size ≥ 0} det {Q} не выводится из {size > 0} det {Q}
Следовательно, надо изменять сами методы

39. Конструкторы по умолчанию
Конструктор должен устанавливать
инвариант класса
Конструкторы по умолчанию часто этого не
делают
Стоит несколько раз подумать, прежде чем
использовать конструктор по умолчанию

40. The Open-Closed Principle
Программные объекты должны быть
открыты для расширения, но в тоже время
закрыты для модификации

41. Импликация на множестве
Пусть P1 → P,
B = { x | P1(x) = 1},
A = { x | P (x) = 1}.
Тогда B ⊂ A.
P ⊨ P1. Говорят, что P –
более слабое условие,
P1 – более сильное.
A
B

42. Построим вывод
{S} cb {P}, {P} c {Q}, {Q} ca {R} ⊦ {S} cb; c; ca {R}
Пусть P → P1, Q1 → Q
Известно, что
{S} cb {P}, {P1} c {Q1}, {Q} ca {R}
Тогда
{P} c {Q} (аксиома вывода)
{S} cb; c; ca {R}

43. Иначе
{S} cb {P}, {P} c {Q}, {Q} ca {R} ⊦ {S} cb; c; ca {R}
Пусть P ↛ P1, но P ^ P1 → P1
Известно, что
{S} cb {P}, {P1} c {Q}, {Q} ca {R}
Тогда
{P1} c {Q} ⊦ {P} if (P1) then c endif {Q}
{S} cb; if(P1) then c endif; ca {R}

44. The Dependency Inversion
Principle
Высокоуровневые компоненты не должны
зависеть от низкоуровневых компонент. И
те, и те должны зависеть от абстракций
(оператора расширения).

45. Правило оператора расширения
Оператор расширения должен допускать:
1. Ослабление предусловий
2. Усиление постусловий

46. Воронка – метафора для
расширения

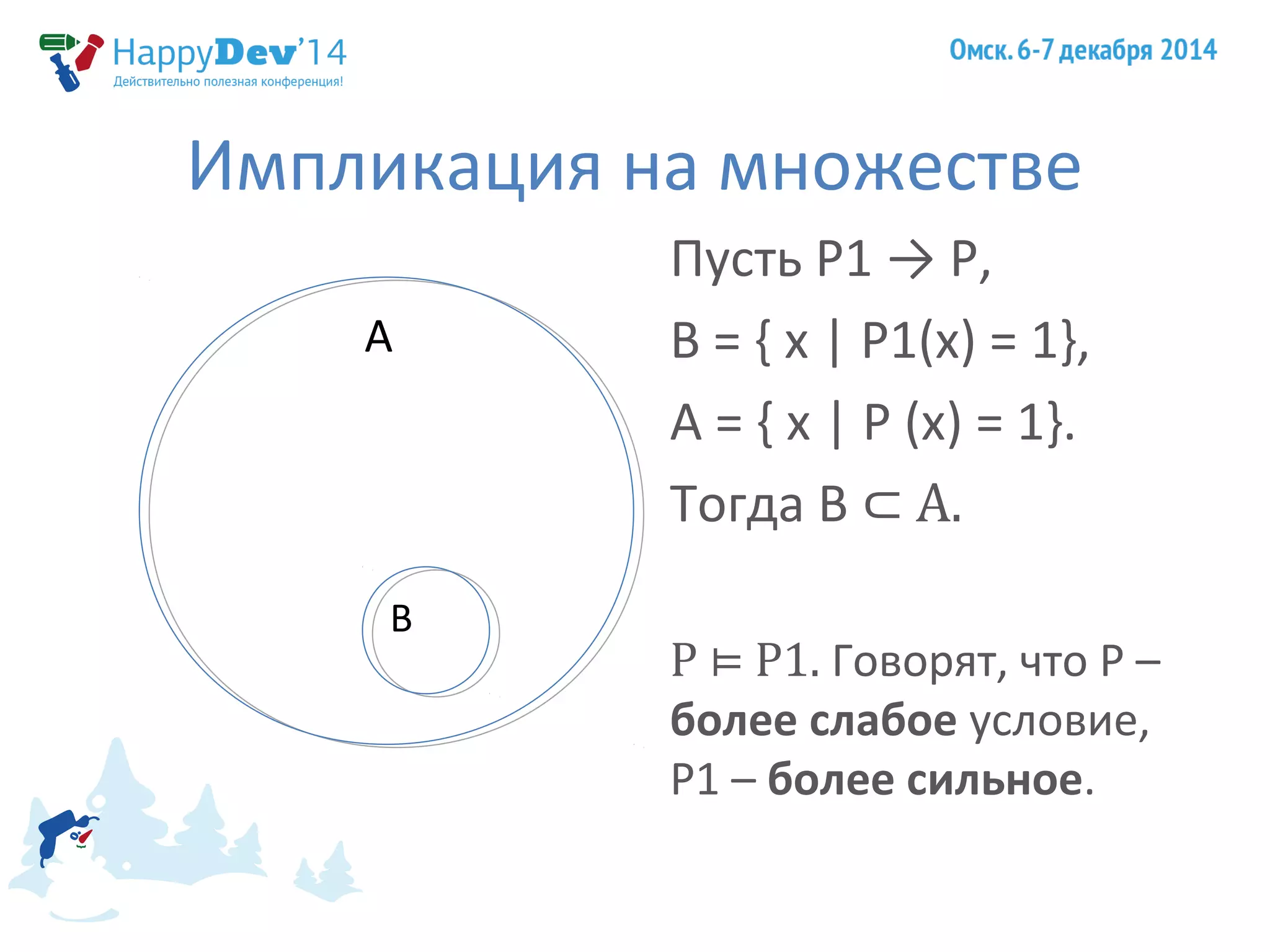
47. Как выглядит расширение?
1. Статический полиморфизм
template <class It, class Op>
void for_each(It begin, It end, Op op)
{
for(; begin != end; ++begin)
op(*begin);
}
int arr[] = {1, 2, 3, 4, 5};
for_each(arr, arr+6, max<int>());

48. Как выглядит расширение?
2. Во время выполнения
– указатель на функцию
void (*f) (int i);
f pf;
pf(5);
– динамический полиморфизм
class Shape {
public:
virtual void Draw() = 0;
};
shape->Draw();

49. Что такое класс?
Это набор методов, возможно полиморфных

50. The Liskov-Substitution Principle
Функции, которые используют ссылки на
базовые классы, должны иметь
возможность использовать объекты
производных классов, не зная об этом.

51. Нарушение OCP, LSP
enum
switch
if-else if-else
Операторы приведения типа

52. Несколько операторов
расширения

53. Жирный интерфейс

54. The Interface Segregation Principle
Класс не должен зависеть от интерфейсов,
которые он не использует

55. А не для классов?
bool (*validator) (Document const & doc);
std::vector<validator> rules = …;
for (int i = 0; i < n; ++i)
if(!rules[i](document))
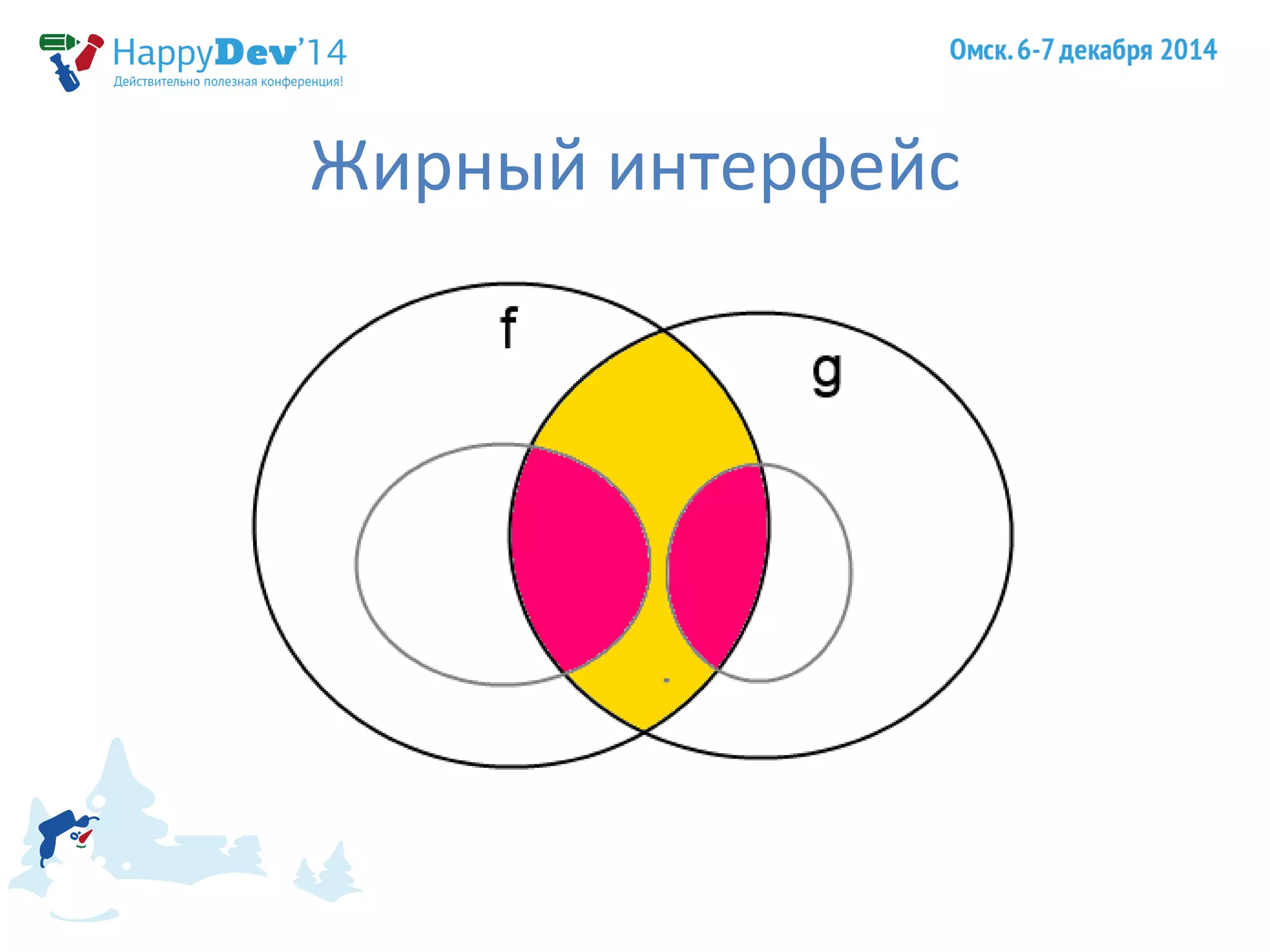
return false;
return true;

56. В каком случае гарантированно удастся
избежать жирного интерфейса?

57. The Single Responsibility Principle
Должна быть ровно
одна причина для
изменения класса

58. А как же функциональщина?

59. В акторной модели не работают?
Тезис Ковальского
Hewitt, Agha 1988
«Вычисления могут
Guarded Horn clause
быть сгруппированы
languages: are they
по логическим
deductive and Logical?
выводам»
Clinger 1981
Foundations Of Actor
Semantics

60. Приглашаю на баркемп
7 декабря
11-00

61. Мы пишем книги
Нерассказанные факты об императивном
программировании
oopguide.ru
Разработка серверов и серверных
приложений
actorsmodelguide.ru

62. Спасибо
Тюменцев Евгений
Директор HWdTech, LLC
Звоните: +7 913 150 22 04
Пишите: etyumentcev@gmail.com
hwdtech.ru