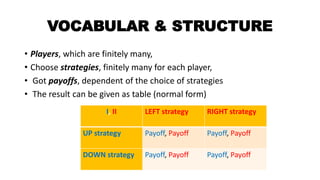
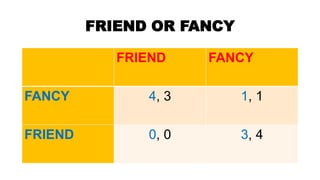
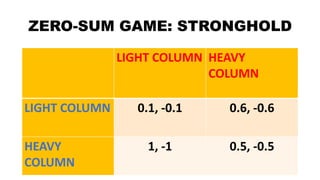
1. The document summarizes key concepts from game theory, including decision making in conflict and cooperation, Nash equilibrium, mixed equilibrium, prisoner's dilemma, ultimatum game, and zero-sum games. 2. It provides examples like the prisoner's dilemma, friend or fancy, and stronghold to illustrate game theory concepts and analyses equilibriums. 3. The document promotes an online English school that teaches game theory and other subjects through virtual classroom lessons.

1. 17 февраля в 21-00 по Москве
Дни науки в Skyeng:
Теория Игр - математика конфликтов

2. GAME THEORY

3. What it is about?
Decision making in conflict and cooperation,
including conflict of interests
Decision-makers are rational and intelligent

4. VOCABULAR & STRUCTURE
• Players, which are finitely many,
• Choose strategies, finitely many for each player,
• Got payoffs, dependent of the choice of strategies
• The result can be given as table (normal form)
I, II LEFT strategy RIGHT strategy
UP strategy Payoff, Payoff Payoff, Payoff
DOWN strategy Payoff, Payoff Payoff, Payoff

5. PRISONERS DILEMMA
GULITY NOT GULITY
GULITY -5, -5 0, -10
NOT GULITY -10, 0 -1, -1

6. NASH EQUILIBRIUM
A CHOICE OF STRATEGIES
SUCH THAT NO PLAYER
INCREASES HIS/HER PAYOFF
WHEN CHANGING HIS/HER STRATEGY
WHILE OTHERS KEEP THEIR

7. FRIEND OR FANCY
FRIEND FANCY
FANCY 4, 3 1, 1
FRIEND 0, 0 3, 4

8. MIXED EQUILIBRIUM
Assume that Player I chooses their fancy with frequency p
Assume that Player II chooses their fancy with frequency q
Payoff = 4p(1-q) + pq + 3(1-p)q = p(4 – 4q + q – 3q) +3q = p(4-6q) + 3q
Payoff = q(4-6p) + 3p

9. ANALYSIS
q>⅔ q<⅔
p>⅔ ↓, ↓ ⅔, ⅔ ↑, ↓ 1, 0
p<⅔ ↓, ↑ 0, 1 ↑, ↑ ⅔, ⅔

10. ASYMMETRIC GAME: ULTIMATUM
ACCEPT REJECT
FAIR 0.5, 0.5 0, 0
UNFAIR 0.8, 0.2 0, 0

11. ULTIMATUM: OTHER APPROACH
Let p be the share Player I proposes to keep for himself
Let q the maximal share Player II is ready to give up
Payoff = p, (1-p) if p ≤ q and 0, 0 otherwise
Equilibriums: p=q and p=1, q=0.

12. ZERO-SUM GAME: STRONGHOLD
LIGHT COLUMN HEAVY
COLUMN
LIGHT COLUMN 0.1, -0.1 0.6, -0.6
HEAVY
COLUMN
1, -1 0.5, -0.5

13. MIXED EQUILIBRIUM
Assume that Player I and Player II choose light column
with frequencies p, q
Payoff = 0.1pq + 0.6p(1-q) + (1-p)q + 0.5 (1-p) (1-q)
= p(0.1q + 0.6(1–q) - q – 0.5(1-q) ) +q + 0.5(1-q)
= p(0.1-q) + 0.5(q +1)
Payoff = - p(0.1-q) - 0.5(q +1) = q(p – 0.5) – 0.1p – 0.5

14. ANALYSIS
q>0.1 q<0.1
p>0.5 ↓, ↑ 0.5, 1 ↑, ↑ 1, 0.1
p<0.5 ↓, ↓ 0, 0.1 ↑, ↓ 0.5, 0

15. 4
• 760 преподавателей
• 8000 учеников
• 629 000 проведенных уроков

16. 3
1. Удобный формат занятий
2. Преподаватель мечты
3. Уникальная платформа для занятий
4. Мобильное приложение для изучения
слов

17. Виртуальный класс,
в котором проходят занятия

22. 32
Запишитесь на вводный урок и введите
промокод GAME THEORY при оплате
Акция действует до 3 марта!
http://skyeng.ru

23. 33
Наши группы в соц.сетях: Читайте нас в почте:
http://school.skyeng.ru/mailing/
Смотрите нас на YouTube
https://www.youtube.com/user/skyengschool
https://vk.com/skyeng
https://facebook.com/SkyEngSch
ool/
https://plus.google.com/+Skyeng
Ru
https://telegram.me/skyeng/
Учите слова в приложении aWord
http://skyeng.ru/go/awordweb