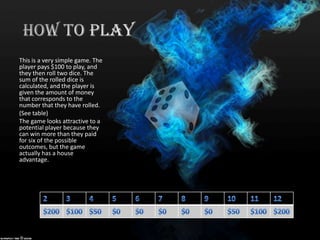
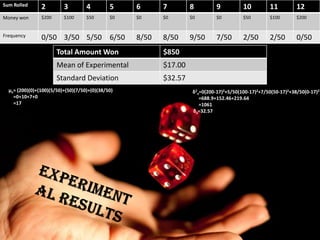
This document summarizes a simple dice game where a player pays $100 to roll two dice. The sum of the dice corresponds to a payout amount in a table. Though some outcomes pay more than $100, the game favors the house due to its odds. An analysis shows the average win is $30.56, so the game price is set at $40. While players may be attracted by higher potential payouts, the house maintains an advantage through its pricing.

2. This is a very simple game. The
player pays $100 to play, and
they then roll two dice. The
sum of the rolled dice is
calculated, and the player is
given the amount of money
that corresponds to the
number that they have rolled.
(See table)
The game looks attractive to a
potential player because they
can win more than they paid
for six of the possible
outcomes, but the game
actually has a house
advantage.

3. X
2
3
4
5
6
7
8
9
10
11
12
P(X)
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
$$$
$200
$100
$50
$0
$0
$0
$0
$0
$50
$100
$200
μx=200(.0556)+100(.111)+50(.1667)+0(.666)
=11.12+11.1+8.335+0
=30.56
Since the average win that I can expect is about $30.56, I
will set the price of the game at $40. The players will
still want to play because they will see that the prizes
are higher than what they paid to play, and
people usually don’t remember to think
about things.
δ2x=.0556(200-30.56)2+.111(100- 30.56)2+.1667(5030.56)2+.666(0-30.56)2
δ2x=1596.2712+535.232+62.998+621.99
δ2x=2816.4912
δx=53.07

4. Sum Rolled
2
3
4
5
6
7
8
9
10
11
12
Money won
$200
$100
$50
$0
$0
$0
$0
$0
$50
$100
$200
Frequency
0/50 3/50 5/50 6/50
8/50
8/50
9/50
7/50
2/50
2/50
0/50
Total Amount Won
$850
Mean of Experimental
$17.00
Standard Deviation
$32.57
μx= (200)(0)+(100)(5/50)+(50)(7/50)+(0)(38/50)
=0+10+7+0
=17
δ2x=0(200-17)2+5/50(100-17)2+7/50(50-17)2+38/50(0-17)2
=688.9+152.46+219.64
=1061
δx=32.57

5. With the results that I have gathered from running a
simulation of this game, I can see that the person who
played lost a lot more money than expected. The player
lost an average of $23 per game, because the player won
an average of $17 per game and the game cost $40 to play.
I have concluded that the
game is difficult to play
because of the low odds
of winning, but the
results achieved fell
within a reasonable range
of the expected values.