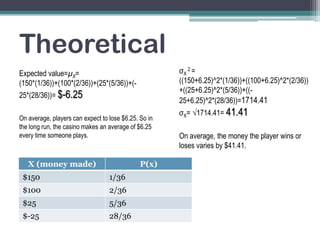
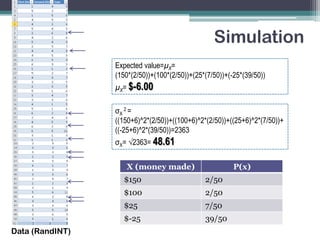
The document describes a dice game where a player pays $25 to roll two dice. If they roll a sum of 2, 3, or 8 they win $175, $125, or $50 respectively. Otherwise they lose the $25. Theoretically, the expected value is a $6.25 loss for the player on average, with a standard deviation of $41.41. A simulation of rolling dice 50 times found an expected loss of $6.00 per play and a standard deviation of $48.61, showing a similar house advantage of around 12% for the casino.

1. Team DD

2. The player pays $25 to play. He/she will roll 2 dice. If he/she
rolls a sum of 2, then he/she will win $175. If he/she rolls a
sum of 3, then he/she will win $125. If he/she rolls a sum of 8,
then he/she will win $50.
If the player rolls anything besides those three sums, he/she
loses the game and wins nothing.

3. Theoretical
σX 2 =
((150+6.25)^2*(1/36))+((100+6.25)^2*(2/36))
+((25+6.25)^2*(5/36))+((25+6.25)^2*(28/36))=1714.41
Expected value=μX=
(150*(1/36))+(100*(2/36))+(25*(5/36))+(25*(28/36))= $-6.25
On average, players can expect to lose $6.25. So in
the long run, the casino makes an average of $6.25
every time someone plays.
X (money made)
P(x)
$150
1/36
$100
2/36
$25
5/36
$-25
28/36
σX= √1714.41= 41.41
On average, the money the player wins or
loses varies by $41.41.

4. Simulation Video
To simulate this game, we will be using the randINT function on our calculator to generate 50 random
numbers between 1 and 6. These 50 numbers will represent what we get when we roll the first die 50
times. Next, we will generate another set of 50 random numbers between 1 and 6 which will represent
what we get when we roll the second die 50 times. Then we will find the sum of the first roll and the
second roll for each of the 50 trials to find out how much money we would win. This will help us figure
out the expected value and the standard deviation of our simulation data.

5. Simulation
Expected value=μX=
(150*(2/50))+(100*(2/50))+(25*(7/50))+(-25*(39/50))
μX= $-6.00
σX 2 =
((150+6)^2*(2/50))+((100+6)^2*(2/50))+((25+6)^2*(7/50))+
((-25+6)^2*(39/50))=2363
σX= √2363= 48.61
X (money made)
P(x)
$150
$100
2/50
$25
7/50
$-25
Data (RandINT)
2/50
39/50

6. Reflection
This game could be a success if put into a casino because it is attractive to the player
while still having a house advantage, as the simulation data and the theoretical values
prove. There is a house advantage of approximately 12% for both (6.25/50=0.125 and
6.00/50=0.12). The theoretical probability shows a slightly larger loss for the player
(which is the expected value) but a smaller standard deviation. A smaller standard
deviation means that the money players lose varies less for the theoretical data than
the simulation data.
This game could be improved upon by having a smaller house advantage. We would
do this by changing the amount of money players pay compared to what they win.