الوثيقة تتناول تقنيات ترميز المصدر، موضحة طريقتين رئيسيتين وهما الكود الثابت والطول المتغير. يتم تفصيل كيفية حساب كفاءة الترميز من خلال معيار شانون، مع تطبيقات عملية تعزز فهم القارئ. كما تتضمن الوثيقة أمثلة رياضية توضح كيفية استخدام هذه التقنيات في إرسال البيانات بكفاءة عالية.

1. 1
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
Chapter Three
Source Coding
‫الـ‬source coding: ‫وهي‬ ‫العمليه‬ ‫هذه‬ ‫التمام‬ ‫طريقتين‬ ‫هناك‬ ‫المصدر‬ ‫في‬ ‫البيانات‬ ‫ترميز‬ ‫اي‬
1- Fixed – length code words ‫للكود‬ ‫ثابت‬ ‫طول‬ ‫باستخدام‬ ‫الترميز‬ ‫طريقة‬
2- Variable – length code words ‫للكود‬ ‫المتغير‬ ‫الطول‬ ‫باستخدام‬ ‫الترميز‬ ‫طريقة‬
1- Fixed – length code words
‫اي‬ ‫ثابت‬ ‫الترميز‬ ‫بعد‬ ‫منها‬ ‫بت‬ ‫كل‬ ‫طول‬ ‫انه‬ ‫باعتبار‬ ‫المرسلة‬ ‫البيانات‬ ‫انتقال‬ ‫كفاءه‬ ‫ايجاد‬ ‫سيتم‬ ‫الطريقة‬ ‫هذه‬ ‫في‬
‫االمث‬ ‫في‬ ‫سنوضح‬ ‫كما‬ ‫االخر‬ ‫البت‬ ‫ياخذها‬ ‫التي‬ ‫للتمثيل‬ ‫البتات‬ ‫عدد‬ ‫نفس‬ ‫ياخذ‬ ‫بت‬ ‫كل‬ ‫انه‬‫الطريقه‬ ‫هذه‬ ‫القادمه‬ ‫له‬
‫غي‬ ‫تعتبر‬‫ر‬‫باعتبارها‬ ‫البديل‬ ‫اليجاد‬ ‫البحث‬ ‫تم‬ ‫لذا‬ ‫العالية‬ ‫بالكفاءه‬ ‫ليست‬ ‫فيها‬ ‫البيانات‬ ‫انتقال‬ ‫كفاءه‬ ‫وعاده‬ ‫مجديه‬
. ‫االرسال‬ ‫عمليه‬ ‫و‬ ‫الخزنية‬ ‫الناحيه‬ ‫من‬ ‫مؤثرة‬
‫هي‬ ‫المعطاه‬ ‫االحتماليات‬ ‫تكون‬ ‫عاده‬ ‫الحاله‬ ‫هذه‬ ‫في‬equal‫من‬ ‫البيانات‬ ‫ارسال‬ ‫كفاءه‬ ‫ولحساب‬ ‫متساويه‬ ‫اي‬
‫االتي‬ ‫القانون‬ ‫خالل‬:
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100%
H(x) = Entropy of x = log2 n
Lc = Length code
‫الستخراج‬Lc‫ال‬ ‫حاله‬ ‫في‬fixed‫االتي‬ ‫الشرط‬ ‫على‬ ‫باالعتماد‬ ‫اليجاده‬ ‫قانونين‬ ‫هناك‬
 If n = 2r
n= [ 2,4,8,16,………] ‫اذن‬ ---- Lc = log2 n bit
 If n ≠ 2r
‫اذن‬ ---- Lc = int [ log2 n] +1 bit
: ‫الفكره‬ ‫التمام‬ ‫مثال‬
Ex: for 10 equiprobable messages coded in a fixed length code then find the
efficiency of code :
‫عباره‬ ‫من‬ ‫متساويه‬ ‫االحتماالت‬ ‫انه‬ ‫بما‬equiprobable
‫اذن‬
H(x) = log2 n = log2 10 = 3.3219 bit/message
Lc = ‫انه‬ ‫بما‬ n ≠ 2r
‫اذن‬ --- Lc = int [log2 (10) ] +1 --- int [ 3.3219] +1  3+1
= 4 bit

2. 2
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100% 
𝟑.𝟑𝟐𝟏𝟗
𝟒
* 100%  0.830475 *100%  ƞ = 83.0475%
2- Variable – length code words
‫نعطي‬ ‫انه‬ ‫من‬ ‫ليصبح‬ ‫تطويره‬ ‫تم‬ ‫لذا‬ ‫االرسال‬ ‫في‬ ‫بطيء‬ ‫ويسبب‬ ‫مجدي‬ ‫غير‬ ‫واحد‬ ‫بطول‬ ‫البت‬ ‫تمثيل‬ ‫انه‬ ‫بما‬
‫الغير‬ ‫فقط‬ ‫يحتااجه‬ ‫ما‬ ‫بت‬ ‫كل‬ ‫سنعطي‬ ‫ال‬ ‫الطريقه‬ ‫هذه‬ ‫في‬ ‫االن‬ ‫البتات‬ ‫من‬ ‫ثابت‬ ‫عدد‬ ‫بت‬ ‫لكل‬‫هذا‬ ‫من‬ ‫الهدف‬
‫البتات‬ ‫عدد‬ ‫تقليل‬ ‫االمر‬‫هناك‬ ‫االرسال‬ ‫وكفاءه‬ ‫سرعة‬ ‫في‬ ‫زيادة‬ ‫يعني‬ ‫مما‬ ‫المرسله‬3‫التمثيل‬ ‫هذا‬ ‫في‬ ‫طرق‬
: ‫كاالتي‬ ‫وهي‬
1- Shannon Code Method
2- Shannon Fano Code
3- Huffman Code
1- Shannon Code :
‫النهائي‬ ‫الطول‬ ‫ايجاد‬ ‫بالتالي‬ ‫مرسل‬ ‫بت‬ ‫كل‬ ‫طول‬ ‫ايجاد‬ ‫في‬ ‫اساسي‬ ‫جدول‬ ‫تكوين‬ ‫اساس‬ ‫على‬ ‫قائمة‬ ‫الطريقة‬ ‫هذه‬
‫للكود‬: ‫كاالتي‬ ‫االرسال‬ ‫كفاءه‬ ‫ايجاد‬ ‫ثم‬ ‫المرسل‬
: ‫كاالتي‬ ‫الجدول‬ ‫من‬ ‫استخراجها‬ ‫يجب‬ ‫التي‬ ‫المعلمات‬
1- Li ‫االتي‬ ‫الشرط‬ ‫حسب‬ ‫قانون‬ ‫من‬ ‫استخراجها‬ ‫يتم‬
If N= (
𝟏
𝟐
)r
N= (
𝟏
𝟐
,
𝟏
𝟒
,
𝟏
𝟖
, … … ) Li = - log2 P(xi)
If N ≠ (
𝟏
𝟐
)r
Li = int [ - log2 P(xi) ] +1
2- Fi
( ‫قيمه‬ ‫احتماليه‬ ‫الول‬ ‫لها‬ ‫قيمه‬ ‫اول‬ ‫تعطي‬ ‫كالتالي‬ ‫تحسب‬0‫هي‬ ‫تكون‬ ‫احتماليه‬ ‫اول‬ ‫مع‬ ‫تجمع‬ ‫ثم‬ )F2‫الناتج‬ ‫ثم‬
‫هي‬ ‫تكون‬ ‫الثانيه‬ ‫االحتماليه‬ ‫مع‬ ‫يجمع‬F3....... ‫باالمثله‬ ‫سيوضح‬ ‫كما‬ ‫وهكذا‬
3- Ci
‫ضرب‬ ‫من‬ ‫تحسب‬Fi‫في‬2‫اما‬ ‫وسيكون‬ ‫الفارزه‬ ‫قبل‬ ‫يوخذ‬ ‫والناتج‬0‫او‬1‫في‬ ‫الفارزه‬ ‫بعد‬ ‫ويضرب‬2‫والناتج‬
‫هو‬ ‫اللي‬ ‫البت‬ ‫طول‬ ‫تغطيه‬ ‫لغايه‬ ‫العمليه‬ ‫تكرر‬ ‫هكذا‬ ‫و‬ ‫الفارزه‬ ‫قبل‬ ‫يؤخذ‬ ‫الحال‬ ‫كذا‬Li‫وكما‬ ‫احتماليه‬ ‫لكل‬
‫اما‬ ‫االتي‬ ‫المثال‬ ‫في‬ ‫موضح‬
0i... ‫موجوده‬ ‫احتماليه‬ ‫لكل‬ ‫النهائي‬ ‫الكود‬ ‫في‬ ‫االصفار‬ ‫عدد‬ ‫فهو‬
Lc = ∑ 𝑳𝒊 ∗ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏
H(x) = ∑ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏 𝒍𝒐𝒈 𝟐 𝑷(𝒙𝒊)
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100%

3. 3
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
Ex: Develop the Shannon code for the following set of messages:
P(x) = [0.3 0.2 0.15 0.12 0.1 0.08 0.05]
Then find:
a) Code efficiency
b) P(0) at the encoder output.
: ‫الجدول‬ ‫بناء‬ ‫هي‬ ‫الحل‬ ‫في‬ ‫خطوه‬ ‫اول‬: ‫كاالتي‬ ‫قيمه‬ ‫االقل‬ ‫الى‬ ‫قيمه‬ ‫االعلى‬ ‫من‬ ‫االحتماليات‬ ‫ترتب‬
OiCiFiLiP(xi)Xi
200020.3X1
20100.330.2X2
21000.530.15X3
210100.6540.12X4
211000.7740.10X5
111010.8740.08X6
1111100.9550.05X7
L (0.3) = int [-log2 (0.3) ] +1 = int [ 1.7369] +1 = 1+1 = 2
L(0.2) = int [ -log2 (0.2) ] +1 = int[ 2.3219]+1 = 2+1 = 3
L(0.15) = int [ -log2 (0.15) ] +1 = int[ 2.7369]+1 = 2+1 = 3
L(0.12) = int [ -log2 (0.12) ] +1 = int[ 3.0588]+1 = 3+1 = 4
L(0.10) = int [ -log2 (0.10) ] +1 = int[ 3.3219]+1 = 3+1 = 4
L(0.08) = int [ -log2 (0.08) ] +1 = int[ 3.6438]+1 = 3+1 = 4
L(0.05) = int [ -log2 (0.05) ] +1 = int[ 4.3219]+1 = 4+1 = 5
============================================
F1 = 0
F2 = F1+ P(x1)  0 + 0.3 = 0.3

4. 4
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
F3 = F2+ P(x2)  0.3 + 0.2 = 0.5
F4 = F3 + P(x3)  0.5 + 0.15 = 0.65
F5= F4 + P(x4)  0.65 + 0.12 = 0.77
F6 = F5 + P(x5)  0.77 + 0.1 = 0.87
F7 = F6 + P(x6)  0.87 + 0.08 = 0.95
C1 = F1 *2
C1 = 0 * 2 = 0
C1 = 0 * 2 = 0 ‫كررت‬3‫من‬ ‫هي‬ ‫االولى‬ ‫االحتماليه‬ ‫النه‬ ‫مرات‬3‫ايجاد‬ ‫يجب‬ ‫البت‬ ‫بطول‬ ‫اي‬ ‫الطول‬ ‫بتات‬
‫الكود‬
C (0.3) = 00
C2 = F2 * 2  L2 = 3
C2 = 0.3 * 2 = 0.6  0
C2 = 0.6 * 2 = 1.2  1
C2 = 0.2 * 2 = 0.4  0
C(0.2) = 010
C3=F3 * 2  L3 = 3
C3 = 0.5 * 2 = 1
C3 = 0 * 2 = 0
C3 = 0 * 2 = 0
C(0.15) = 100
C4 = F4 * 2  L4 = 4
C4 = 0.65 * 2 = 1.3  1
C4 = 0.3 * 2 = 0.6  0
C4 = 0.6 * 2 = 1.2  1
C4 = 0.2 * 2 = 0.4  0

5. 5
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
C(0.12) = 1010
C5 = F5 * 2  L5 = 4
C5 = 0.77 * 2 = 1.54  1
C5 = 0.54 * 2 = 1.08  1
C5 = 0.08 * 2 = 0.16  0
C5= 0.16 * 2 = 0.32  0
C(0.10) = 1100
C(0.08) = F6 * 2  L6 = 4
C6 = 0.87 * 2 = 1.74  1
C6 = 0.74 * 2 = 1.48  1
C6 = 0.48 * 2 = 0.96  0
C6 = 0.96 * 2 = 1.92  1
C(0.08) = 1101
C(0.05) = F7 * 2  L7 = 5
C7 = 0.95 * 2 = 1.9  1
C7 = 0.9 * 2 = 1.8  1
C7 = 0.8 * 2 = 1.6  1
C7= 0.6 * 2 = 1.2  1
C7 = 0.2 * 2 = 0.4  0
C(0.05) = 11110
0i = ‫النهائي‬ ‫الكود‬ ‫في‬ ‫االصفار‬ ‫عدد‬
‫وبعد‬ ‫االن‬: ‫وكالتالي‬ ‫الكفاءه‬ ‫حساب‬ ‫سيتم‬ ‫منه‬ ‫اعاله‬ ‫الجدول‬ ‫تكوين‬ ‫من‬ ‫االنتهاء‬
H(x) = - ∑ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏 𝒍𝒐𝒈 𝟐 𝑷(𝒙𝒊)
H(x) = - [ 0.3 log2 0.3 + 0.2 log2 0.2 + 0.15 log2 0.15 + 0.12 log2 0.12 + 0.1 log2 0.1
+ 0.08 log2 0.08 + 0.05 log2 0.05]

6. 6
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
H(x) = - [ 0.5210 + 0.4643 + 0.4105 + 0.3670 + 0.3321 + 0.2915 + 0.2160]
H(x) = 2.6024 bit/message
Lc = ∑ 𝑳𝒊 ∗ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏
Lc = [ 0.3 * 2 + 0.2 * 3 + 0.15 * 3 + 0.12 * 4 + 0.1 * 4 + 0.08 * 4 + 0.05*5]
Lc = [ 0.6 + 0.6 + 0.45 + 0.48 + 0.4 + 0.32 + 0.25]
Lc = 3.1 bit
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100%  ƞ =
𝟐.𝟔𝟎𝟐𝟒
𝟑.𝟏
* 100%  ƞ = 𝟎. 𝟖𝟑𝟗𝟒 *
100%
 ƞ = 𝟖𝟑. 𝟗𝟒𝟖𝟑%
b) P(0) at the encoder output.
P(0) =
∑ 𝑷( 𝒙𝒊) ∗ 𝟎 𝒊
𝟕
𝒋=𝟏
𝑳𝒄

P(0) =
[ 𝟎.𝟑∗𝟐+𝟎.𝟐∗𝟐+𝟎.𝟏𝟓∗𝟐+𝟎.𝟏𝟐∗𝟐+𝟎.𝟏∗𝟐+𝟎.𝟎𝟖∗𝟏+𝟎.𝟎𝟓∗𝟏]
𝟑.𝟏
P(0) =
𝟏.𝟖𝟕
𝟑.𝟏
= 0.6032 ( ‫الــ‬ ‫احتمالية‬0)
( ‫ال‬ ‫احتمالية‬ ‫اليجاد‬1: ‫يكون‬ ‫االحتماليه‬ ‫قانون‬ ‫حسب‬ )
P(0) + P(1) = 1
0.6032 + P(1) = 1
P(1) = 1 – 0.6032
P(1) = 0.3968

7. 7
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
2) Shannon – Fano code:
‫بحيث‬ ‫مجموعه‬ ‫احتمالين‬ ‫اول‬ ‫مجاميع‬ ‫الي‬ ‫االحتماليات‬ ‫تجزئه‬ ‫على‬ ‫الكود‬ ‫ايجاد‬ ‫في‬ ‫سنعتمد‬ ‫الطريقة‬ ‫هذه‬ ‫في‬
‫يكون‬ ‫احيانا‬ ‫ممكن‬ ‫فارق‬ ‫باقل‬ ‫االمكان‬ ‫قدر‬ ‫سوية‬ ‫االحتماالت‬ ‫باقي‬ ‫جمع‬ ‫لحاصل‬ ‫مقارب‬ ‫جمعهم‬ ‫حاصل‬ ‫يكون‬
‫مجم‬ ‫وحده‬ ‫هو‬ ‫يؤخذ‬ ‫كبير‬ ‫رقم‬ ‫هو‬ ‫االول‬ ‫االحتمال‬‫االحتماليات‬ ‫نقسم‬ ‫انه‬ ‫المهم‬ ‫ثانيه‬ ‫مجموعه‬ ‫كلهم‬ ‫الباقي‬ ‫و‬ ‫وعه‬
‫احتماالتها‬ ‫لجميع‬ ‫االولى‬ ‫للمجموعه‬ ‫نعطي‬ ‫التقسيم‬ ‫بعد‬ ‫مجموعتين‬ ‫الى‬0‫الثانيه‬ ‫المجموعة‬ ‫و‬1‫نعود‬ ‫ثم‬
‫االول‬ ‫ونعطي‬ ‫مجموعتين‬ ‫نقسمهم‬ ‫فقط‬ ‫احتمالين‬ ‫من‬ ‫هي‬ ‫التي‬ ‫نفسها‬ ‫االولى‬ ‫المجموعه‬ ‫لتقسيم‬0‫الثاني‬ ‫و‬1
‫االحتما‬ ‫ثم‬‫جمع‬ ‫حاصل‬ ‫تكون‬ ‫ان‬ ‫االعتبار‬ ‫بنظر‬ ‫االخذ‬ ‫مع‬ ‫الطريقة‬ ‫وبنفس‬ ‫مجموعتين‬ ‫تقسم‬ ‫كذلك‬ ‫الباقيه‬ ‫الت‬
‫المجموعة‬ ‫نعطي‬ ‫الحال‬ ‫وكذا‬ ‫الثانيه‬ ‫المجموعه‬ ‫جمع‬ ‫لحاصل‬ ‫ممكن‬ ‫حد‬ ‫اقرب‬ ‫الى‬ ‫مقارب‬ ‫االولى‬ ‫المجموعه‬
‫االولى‬0‫الثانيه‬ ‫و‬1‫قسمت‬ ‫جميها‬ ‫االحتماالت‬ ‫فيها‬ ‫يكون‬ ‫التي‬ ‫الحاله‬ ‫الى‬ ‫نصل‬ ‫ان‬ ‫الى‬‫وعندها‬ ‫حده‬ ‫على‬ ‫كل‬
: ‫االتي‬ ‫المثال‬ ‫في‬ ‫سيوضح‬ ‫كما‬ ‫اكتمل‬ ‫الكود‬ ‫يكون‬
Example:
Develop the Shannon – Fano code for the following set of messages,
p(x) = [ 0.35 0.2 0.15 0.12 0.1 0.08] then find the code efficiency.
Solution
Xi P(xi) Code Li
X1 0.35 00 2
X2 0.2 01 2
X3 0.15 100 3
X4 0.12 101 3
X5 0.10 110 3
X6 0.08 111 3
‫انه‬ ‫بما‬: ‫المجموعات‬ ‫يتقسيم‬ ‫االن‬ ‫نيدء‬ ‫بالحل‬ ‫نستمر‬ ‫اذن‬ ‫متقاربان‬ ‫الرقمين‬
Lc = ∑ 𝑳𝒊 ∗ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏
‫اولى‬ ‫مجموعة‬0.27
‫مجموعة‬‫ثانية‬180.
‫اولى‬ ‫مجموعة‬0.55
‫مجموعة‬‫ثانية‬0.45
‫هيه‬ ‫االعلى‬ ‫المجموعة‬ ً‫ا‬‫دائم‬
‫االكبر‬‫باالعلى‬ ‫تكون‬ ‫و‬

8. 8
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
Lc = [ 0.35 * 2 + 0.2 * 2 + 0.15*3 + 0.12*3 + 0.1*3 + 0.08*3 ]
=[0.7+0.4+0.45+0.36+0.3+0.24] = 2.45bit
H(x) = − ∑ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏 𝒍𝒐𝒈 𝟐 𝑷(𝒙𝒊) = -[ 0.35 log2 0.35 + 0.2 log20.2 + 0.15 log20.15
+ 0.12 log2 0.12 + 0.1 log2 0.1 + 0.08 log2 0.08]
= -[0.5301+0.4643+0.4105+0.3670+0.3321+0.2915]= 2.3955bit/symbol
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100%  ƞ =
𝟐.𝟑𝟗𝟓𝟓
𝟐.𝟒𝟓
* 100% = 0.9777*100% =
97.77%

9. 9
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
3) Huffman code:
‫من‬ ‫احتمالين‬ ‫اقل‬ ‫جمع‬ ‫وبعدها‬ ‫تنازليا‬ ‫االصغر‬ ‫الى‬ ‫االكبر‬ ‫من‬ ‫االحتماالت‬ ‫ترتيب‬ ‫على‬ ‫تعتمد‬ ‫الطريقة‬ ‫هذه‬ ‫في‬
= ‫الناتج‬ ‫فيها‬ ‫يكون‬ ‫جمع‬ ‫عمليه‬ ‫اخر‬ ‫الى‬ ‫نصل‬ ‫ان‬ ‫الى‬ ‫احتمالين‬ ‫اقل‬ ‫فيها‬ ‫يجمع‬ ‫مره‬ ‫كل‬ ‫عند‬ ‫الترتيب‬ ‫اعاده‬ ‫ثم‬1
: ‫االتي‬ ‫المثال‬ ‫في‬ ‫موضح‬ ‫وكما‬
Example:
Develop the Huffman code for the following set of symbols:
HGFEDCBASymbol
0.040.070.10.060.050.40.180.1Probability
:Solution
R6R5R4R3R2R1P(x)Symbol
0.60.400.400.400.400.400.40C
0.40.370.230.190.180.180.18B
0.230.190.180.130.100.10A
0.180.130.100.100.10F
0.100.100.090.07G
0.090.070.06E
0.060.05D
0.04H
‫ونضعه‬ ‫عقده‬ ‫كل‬ ‫نهاية‬ ‫في‬ ‫الرقم‬ ‫قراءه‬ ‫ثم‬ ‫االسهم‬ ‫حسب‬ ‫منها‬ ‫كل‬ ‫مسار‬ ‫نتبع‬ ‫احتماليه‬ ‫كل‬ ‫كود‬ ‫الستخراج‬
‫االول‬ ‫الرقم‬ ‫بعد‬ ‫الرقم‬ ‫ونضع‬ ‫عندها‬ ‫الرقم‬ ‫وقراءه‬ ‫االخرى‬ ‫العقدة‬ ‫ال‬ ‫للوصول‬ ‫المسار‬ ‫تكمله‬ ‫ثم‬ ‫من‬ ‫اليمين‬ ‫في‬
‫يكو‬ ‫وعندها‬ ‫االحتماليه‬ ‫هذه‬ ‫مسار‬ ‫ضمن‬ ‫عقده‬ ‫اخر‬ ‫الى‬ ‫نصل‬ ‫ان‬ ‫الى‬ ‫وهكذا‬‫اكتمل‬ ‫قد‬ ‫االحتماليه‬ ‫هذه‬ ‫كود‬ ‫ن‬
: ‫االحتماالت‬ ‫لباقي‬ ‫الحال‬ ‫وكذا‬
Symbol A B C D E F G H
Probability 0.1 0.18 0.4 0.05 0.06 0.1 0.07 0.04
Code word 011 001 1 00010 0101 0000 0100 00011
Li 3 3 1 5 4 4 4 5
0
1
1
1
0 1
1
1
0
0
0
0
0
1

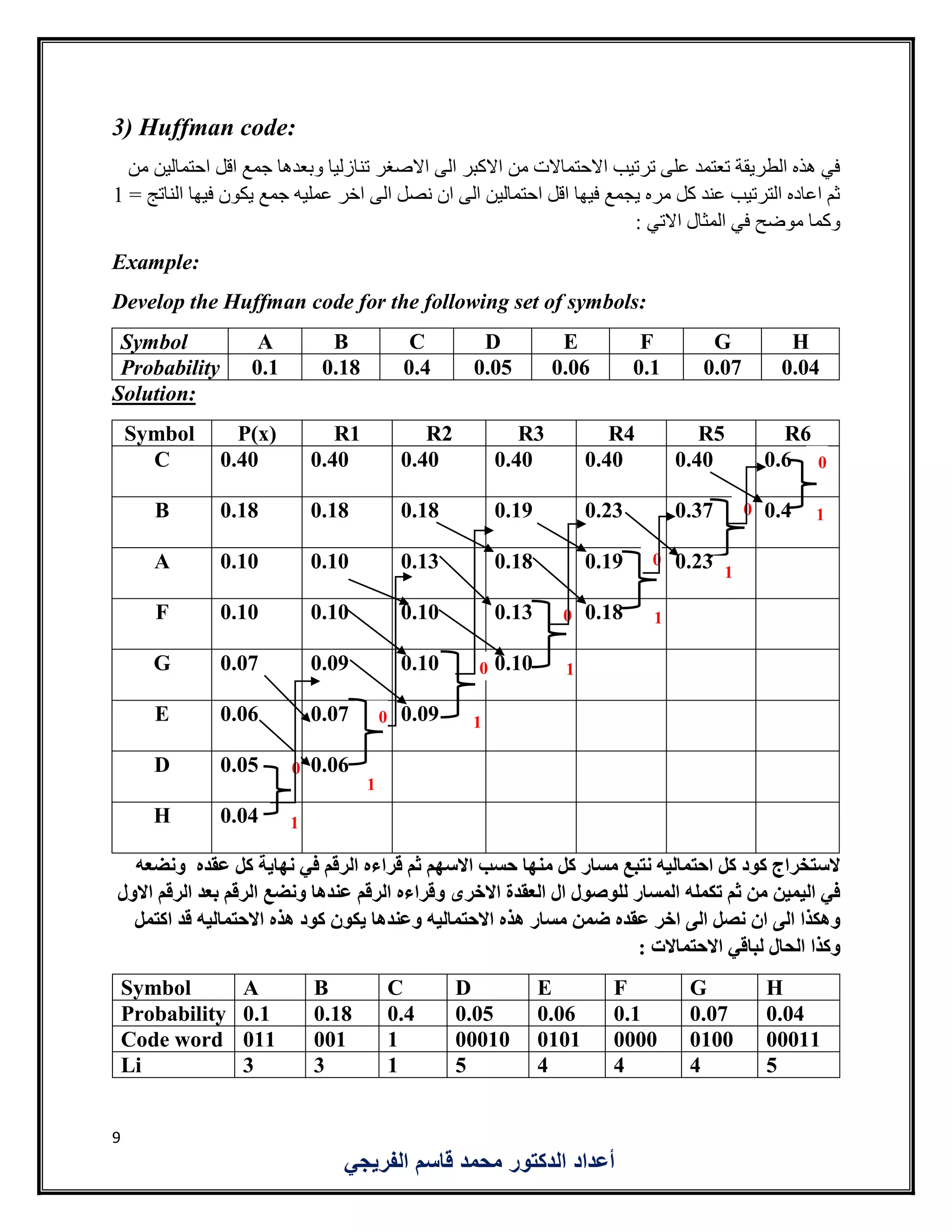
10. 10
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
‫يجب‬ ‫الكفاءة‬ ‫لحساب‬ ‫احتمالية‬ ‫لكل‬ ‫الكود‬ ‫حساب‬ ‫بعد‬: ‫كاالتي‬ ‫الكود‬ ‫طول‬ ‫ثم‬ ‫االنتروبي‬ ‫حساب‬
H(x) = − ∑ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏 𝒍𝒐𝒈 𝟐 𝑷(𝒙𝒊)  - [0.1 log2 0.1 + 0.18 log2 0.18 + 0.4 log2 0.4
+ 0.05 log2 0.05 + 0.06 log2 0.06 + 0.1 log2 0.1 + 0.07 log2 0.07 + 0.04 log2 0.04 ]
= 2.552 bit/symbol
Lc = ∑ 𝑳𝒊 ∗ 𝑷(𝒙𝒊)𝒏
𝒊=𝟏
Lc = [ 0.1*3 + 0.18*3 + 0.4*1 + 0.05*5 + 0.06*4 + 0.1*4 + 0.07*4 + 0.04*5 ] =
2.61 bit
ƞ =
𝑯(𝒙)
𝑳𝒄
* 100%  ƞ =
𝟐.𝟓𝟓𝟐
𝟐.𝟔𝟏
* 100% =0.9777*100% = 97.77%
 Data Compression
‫زيادة‬ ‫بالتالي‬ ‫الرسالة‬ ‫في‬ ‫المرسلة‬ ‫البتات‬ ‫عدد‬ ‫لتقليل‬ ‫البيانات‬ ‫ضغط‬ ‫نستخدم‬‫سرعته‬ ‫و‬ ‫االرسال‬ ‫عملية‬ ‫كفاءة‬
.
: ‫هي‬ ‫البيانات‬ ‫لضغط‬ ‫طريقتين‬ ‫هناك‬
1- Lossless data compression
2- Lossy data compression
‫هو‬ ‫واقعا‬ ‫المستخدم‬Lossless: ‫هي‬ ‫فيه‬ ‫مستخدمة‬ ‫تقنية‬ ‫واهم‬ ‫الضغط‬ ‫عملية‬ ‫اثناء‬ ‫الفقد‬ ‫قليل‬ ‫اي‬
Run – Length Encoding (RLE):
Example :input
:AAABBCCCCDEEEEEEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAA
Solution: 3A2B4C1D6E38A
‫من‬ ‫بدال‬ ‫البيانات‬ ‫ضغط‬ ‫تم‬ ‫هنا‬ ‫نالحظ‬54‫الى‬ ‫بت‬13: ‫االتي‬ ‫القانون‬ ‫من‬ ‫تحسب‬ ‫هي‬ ‫الضغط‬ ‫نسبة‬ ‫انه‬ ‫اي‬ ‫بت‬
‫الضغط‬ ‫قبل‬ ‫المرسلة‬ ‫البتات‬ ‫عدد‬
‫الضغط‬ ‫بعد‬ ‫المرسلة‬ ‫البتات‬ ‫عدد‬
So :
𝟓𝟒
𝟏𝟑

11. 11
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
Example: Consider these repeated pixels values in an image ...
(000000000000555500000000)
We could represent them more efficiently as (12, 0)(4,5)(8,0) 24 bytes reduced
to 6 which gives a compression ratio of 24/6 = 4:1.
Example: Original Sequence (1 Row): 111122233333311112222 can be encoded
as:
(4,1),(3,2),(6,3),(4,1),(4,2). 21 bytes reduced to 10 gives a compression ratio of
21/10 =21:10.
Example: Original Sequence (1 Row): – HHHHHHHUFFFFFFFFFFFFFF
can be
encoded as: (7, H), (1, U), (14, F). 22 bytes reduced to 6 gives a compression
ratio of 22/6= 11:3.
Saving Ratio:
‫قبل‬ ‫المرسلة‬ ‫البتات‬ ‫عدد‬ ‫تقسيم‬ ‫خالل‬ ‫من‬ ‫انه‬ ‫ذكرنا‬ ‫البيانات‬ ‫على‬ ‫تنفيذه‬ ‫تم‬ ‫التي‬ ‫الضغط‬ ‫نسبة‬ ‫لمعرفة‬
‫الضغط‬N1‫الضغط‬ ‫بعد‬ ‫المرسلة‬ ‫البياتات‬ ‫نسبة‬ ‫الى‬N2( ‫بــ‬ ‫هذا‬ ‫القسمة‬ ‫ناتج‬ ‫وتسمى‬Cr‫اي‬ )
Compression ratio: ‫االتي‬ ‫القانون‬ ‫من‬ ‫ويحسب‬
𝑪𝒓 =
𝑵𝟏
𝑵𝟐
: ‫االتي‬ ‫القانون‬ ‫من‬ ‫تحسب‬ ‫الضغط‬ ‫عملية‬ ‫بعد‬ ‫فعال‬ ‫المخزنة‬ ‫البيانات‬ ‫نسبة‬ ‫اما‬
𝑺𝒓 =
(𝑵𝟏−𝑵𝟐)
𝑵𝟏
* 100%
Example: a 5 Megabyte image is compressed into a 1 Megabyte image, the
savings ratio is defined as
𝑪𝒓 =
𝟓
𝟏
= 5
𝑺𝒓 =
(𝟓−𝟏)
𝟓
* 100% =
𝟒
𝟓
* 100% = 0.8*100 = 80%

12. 12
‫الفريجي‬ ‫قاسم‬ ‫محمد‬ ‫الدكتور‬ ‫أعداد‬
This ratio indicates that 80% of the uncompressed data has been eliminated in
the compressed encoding.
Example : Use RLE to compress the following data stream, find compression
ratio and saving percentage [aaaadcccccbbbbbbbbbaaaaaabbbbbbbbbbccc]
Solution:
(4,a) ,(1,d), (5,c), (9,b), (6,a), (10,b), (3,c)
N1(size before compression)=38
N2 (size after compression)=14
𝐶𝑟 (𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛 𝑟𝑎𝑡𝑖𝑜) =𝑁1/𝑁2 = 38 / 14
Cr = 19:4
𝑆𝑎𝑣𝑖𝑛𝑔 𝑝𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 = 𝑁1 − 𝑁2 / 𝑁1∗ 100 = 38 – 14 / 38 ∗ 100
Sp= 63.157%