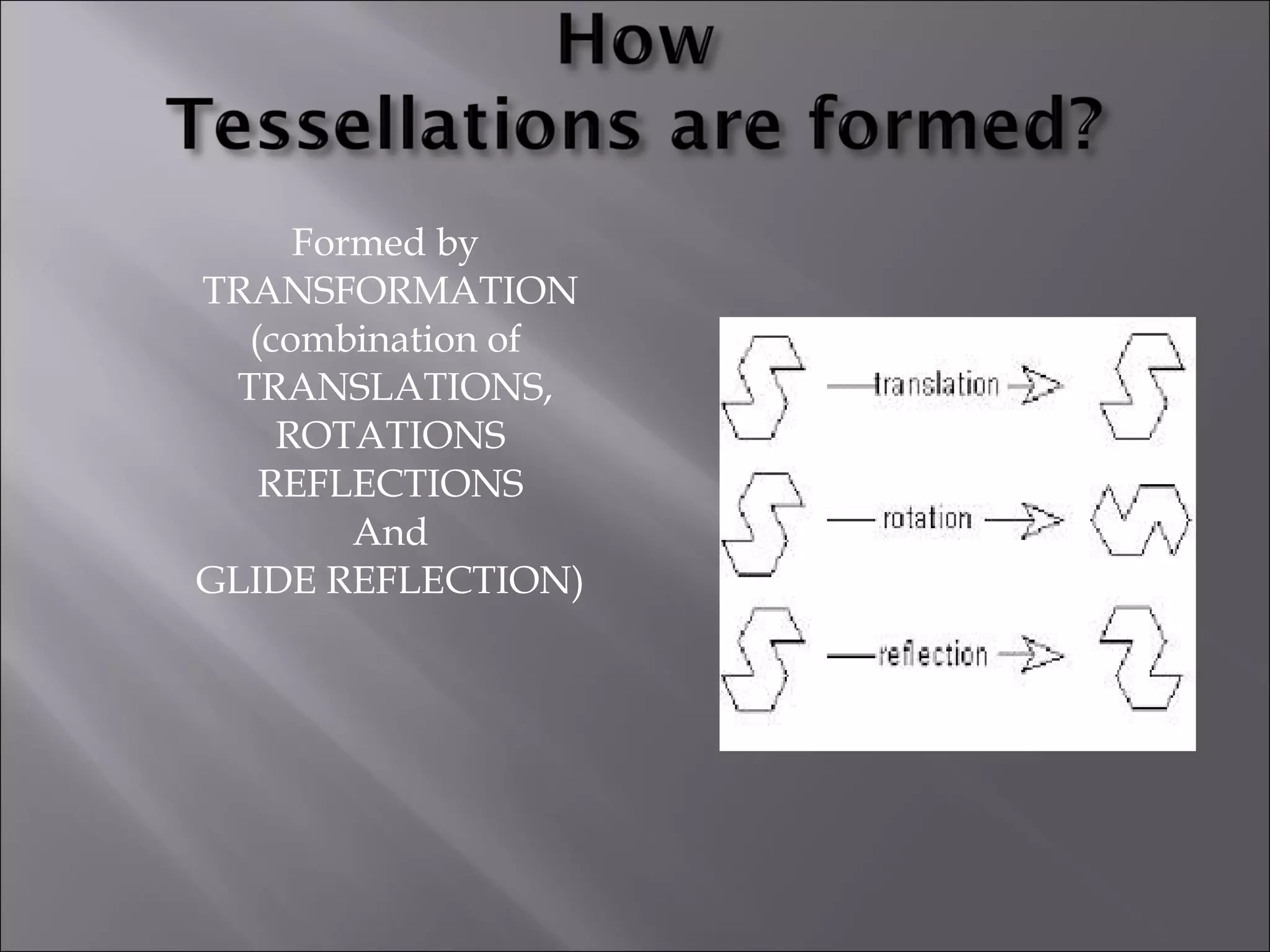
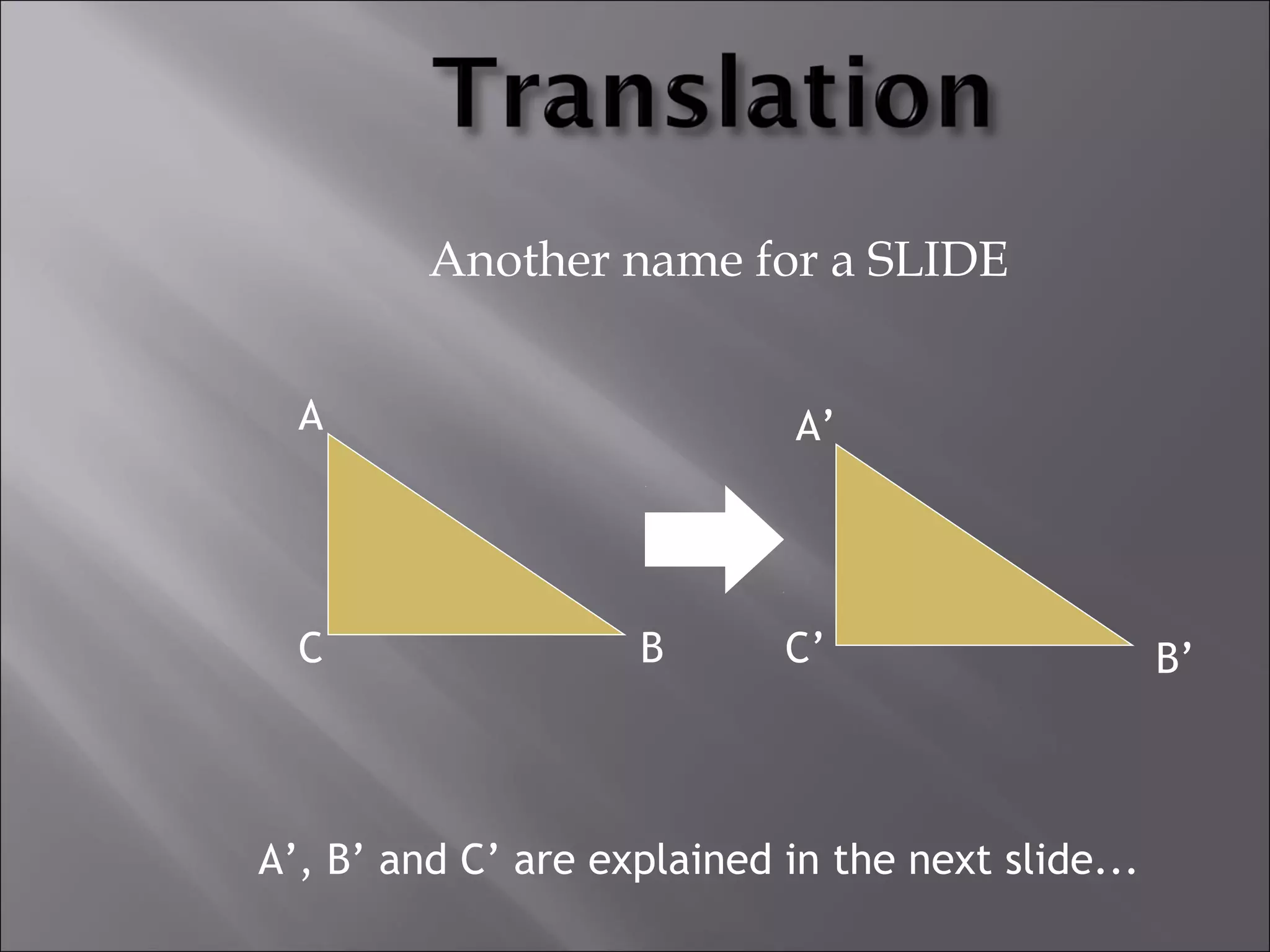
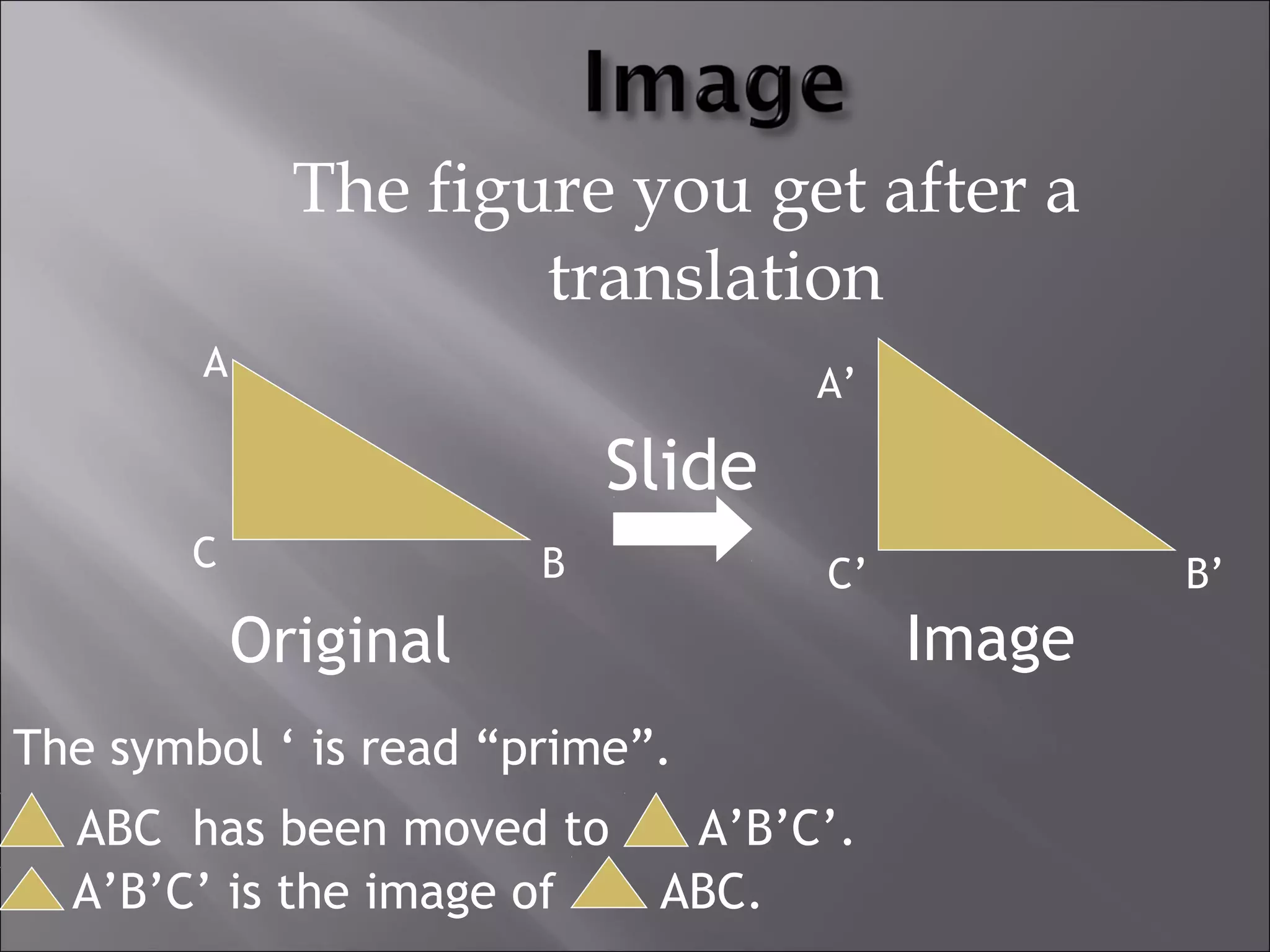
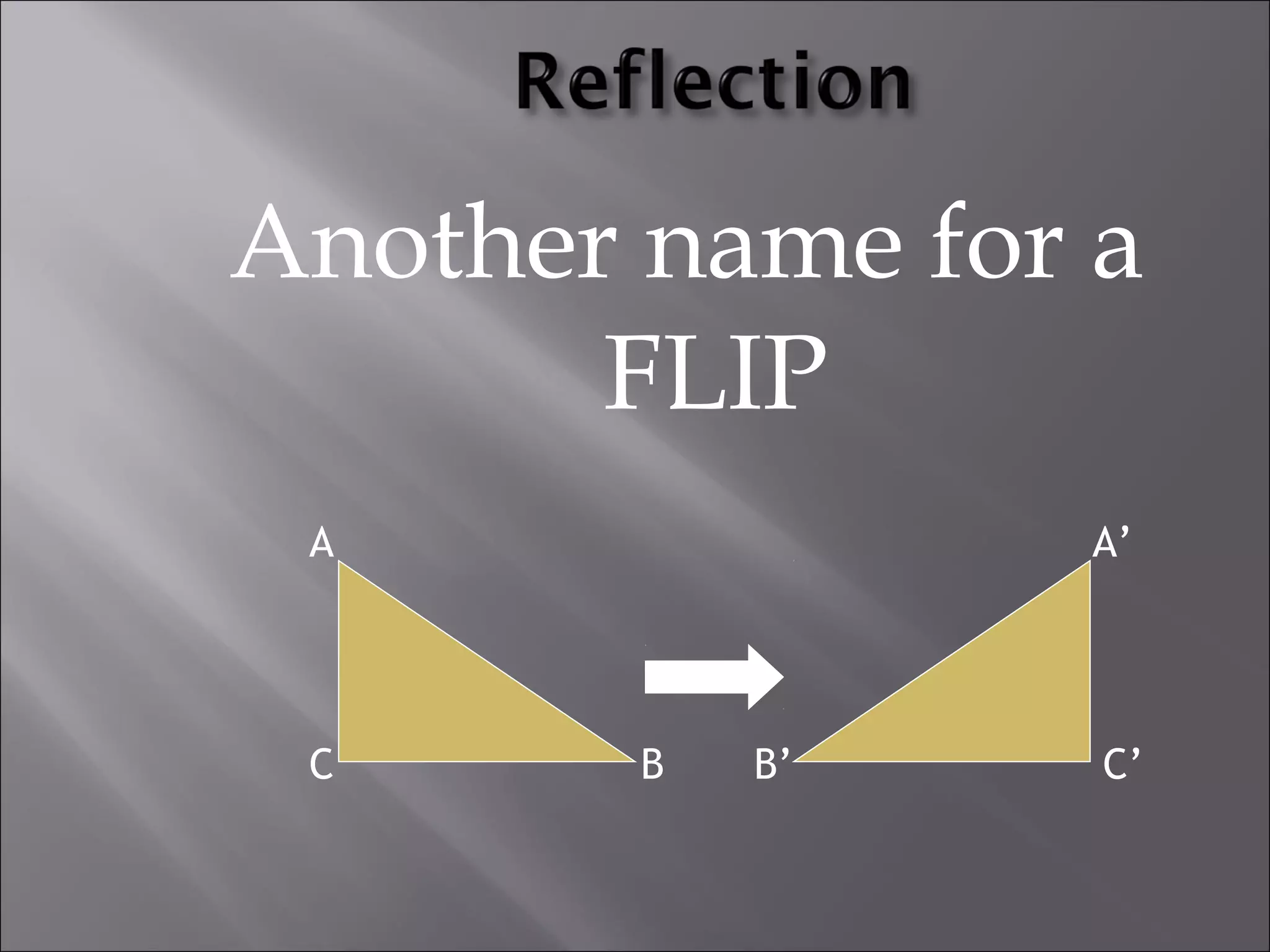
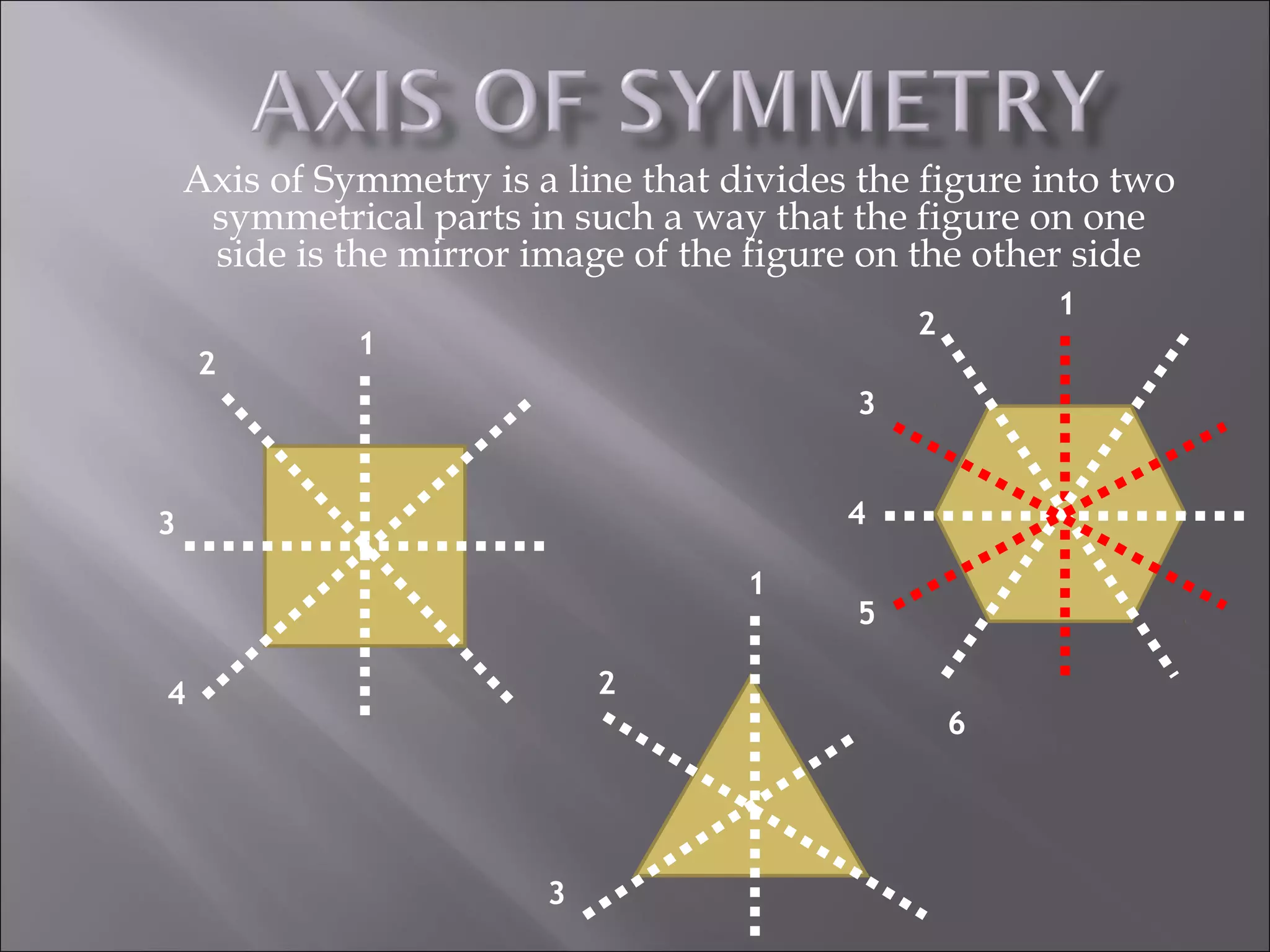
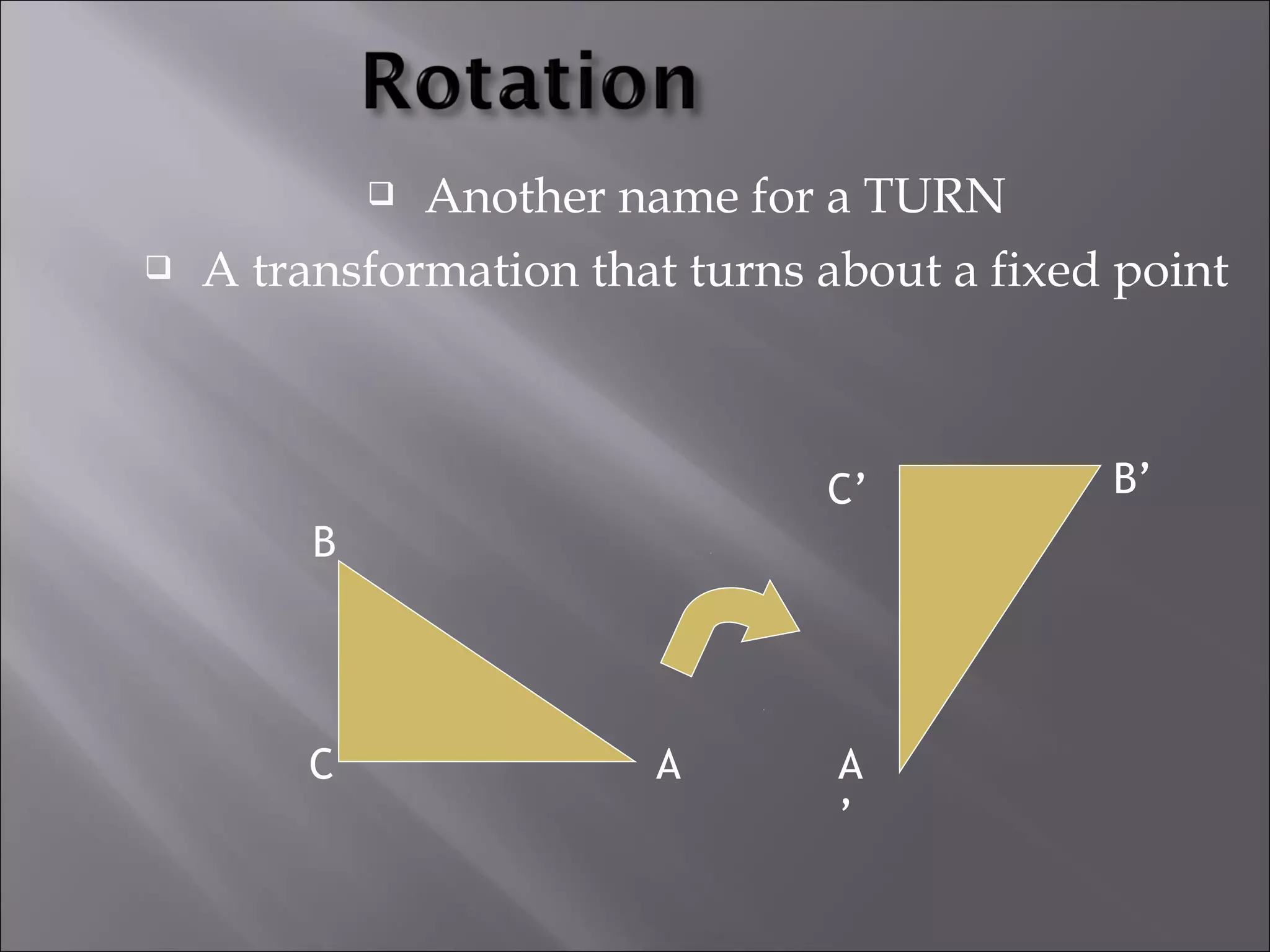
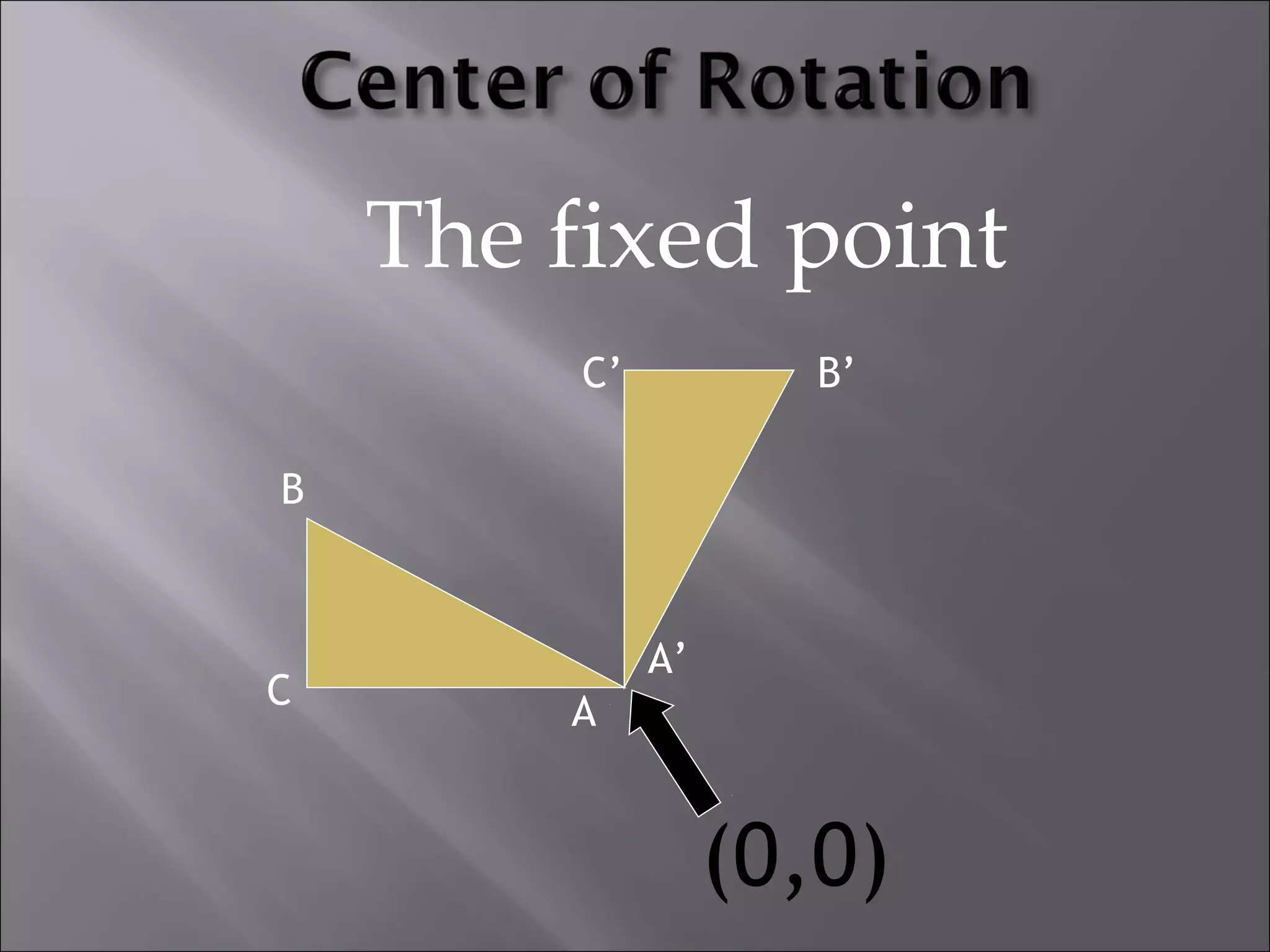
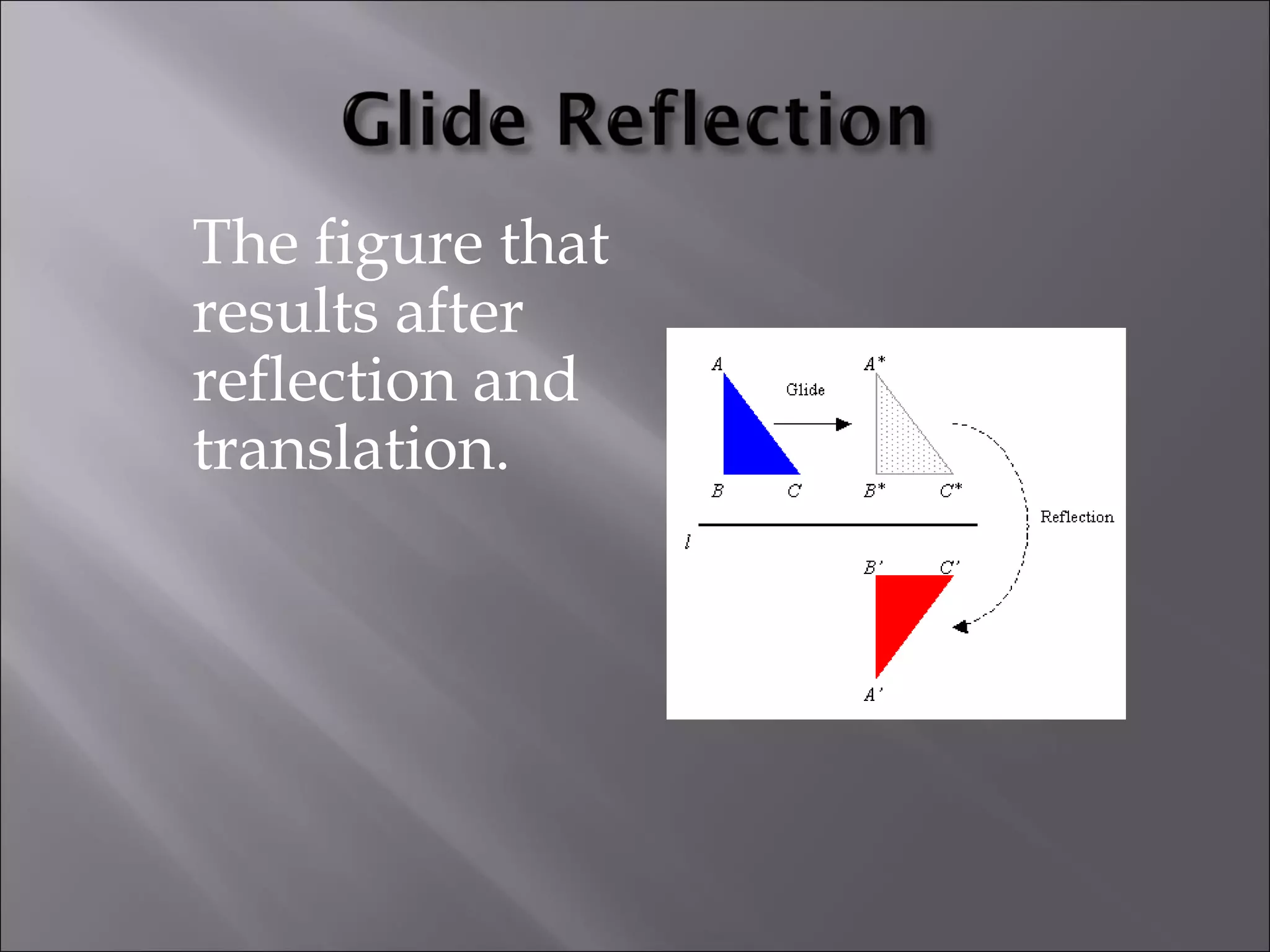
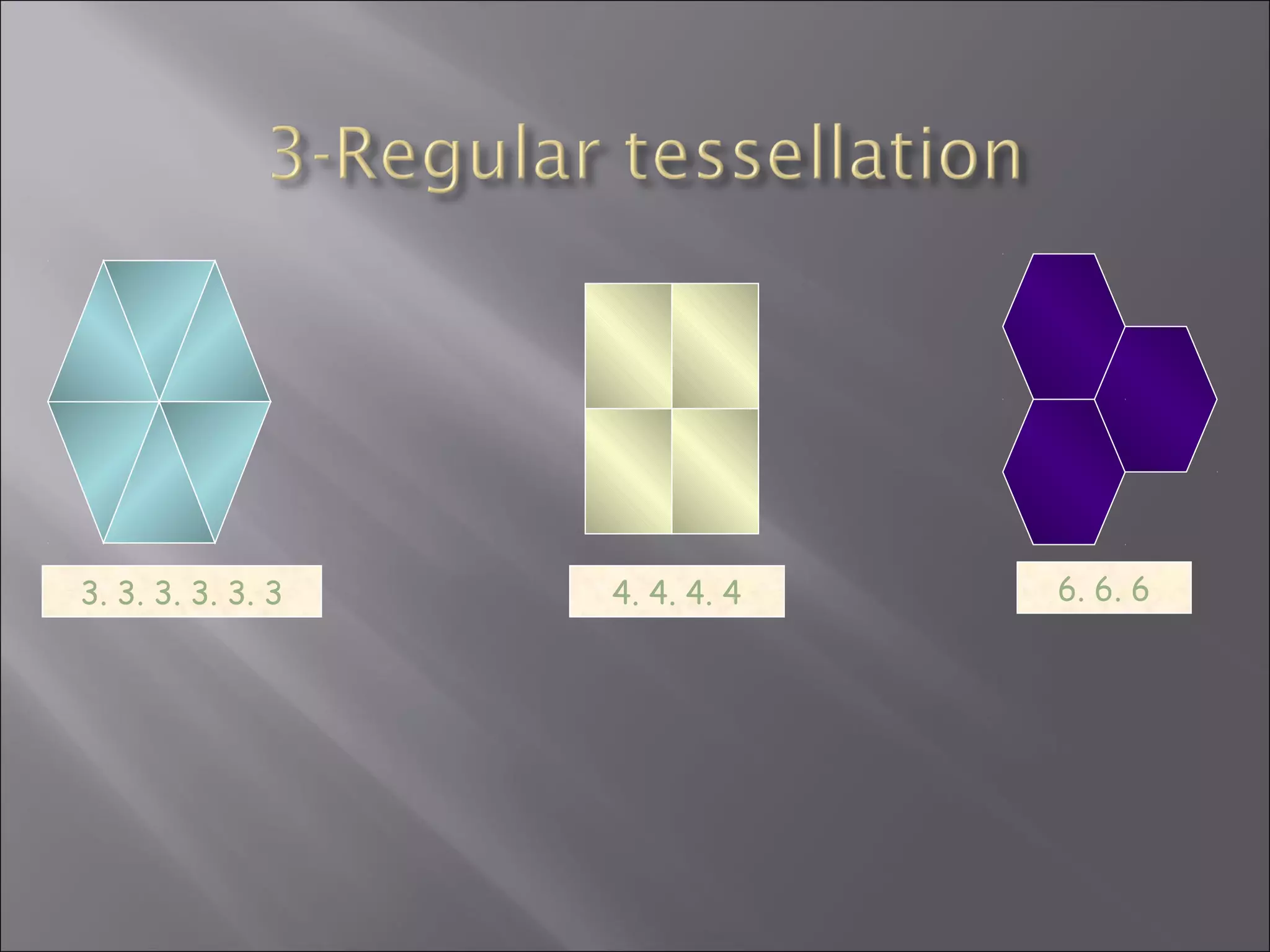
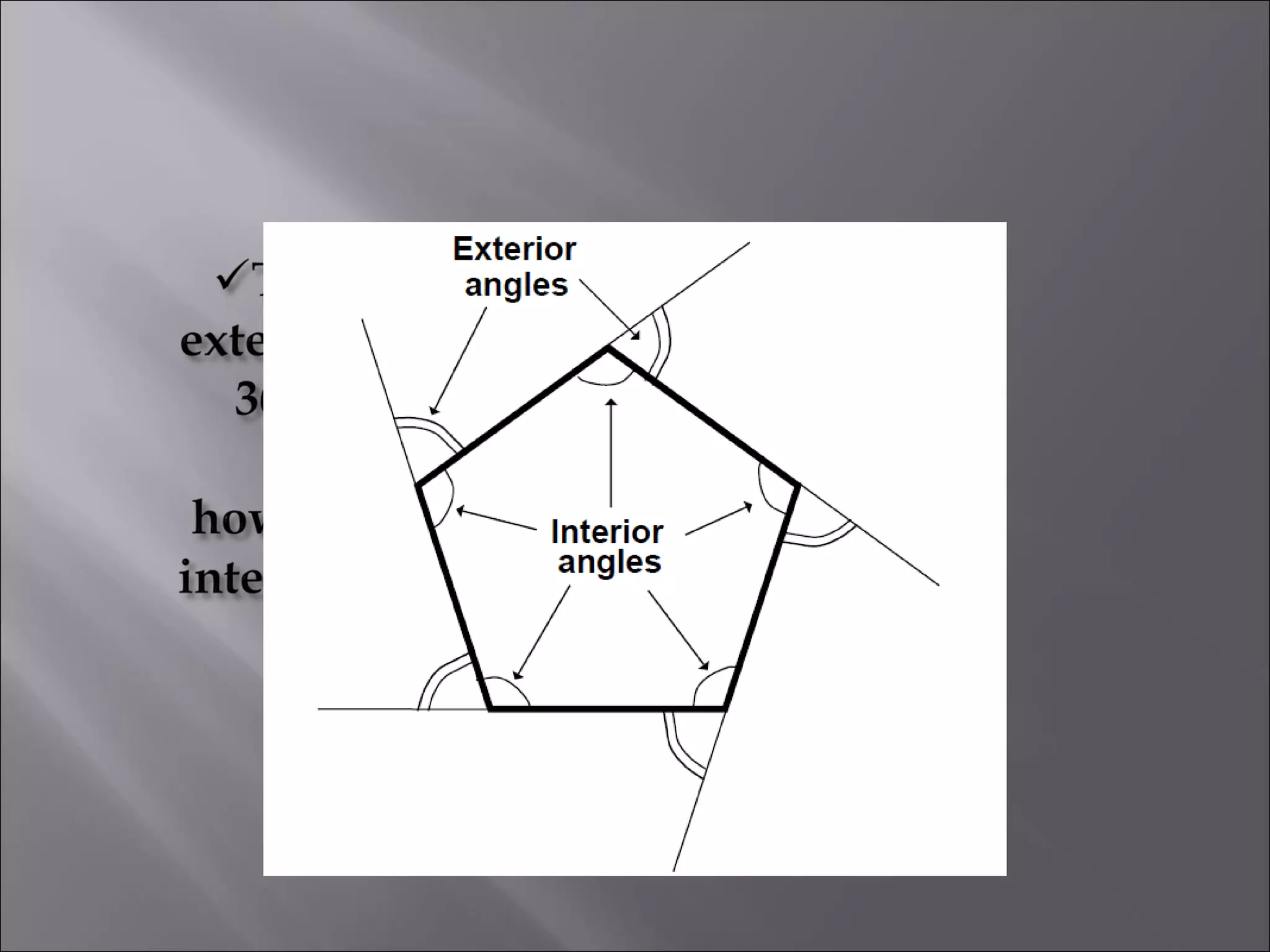
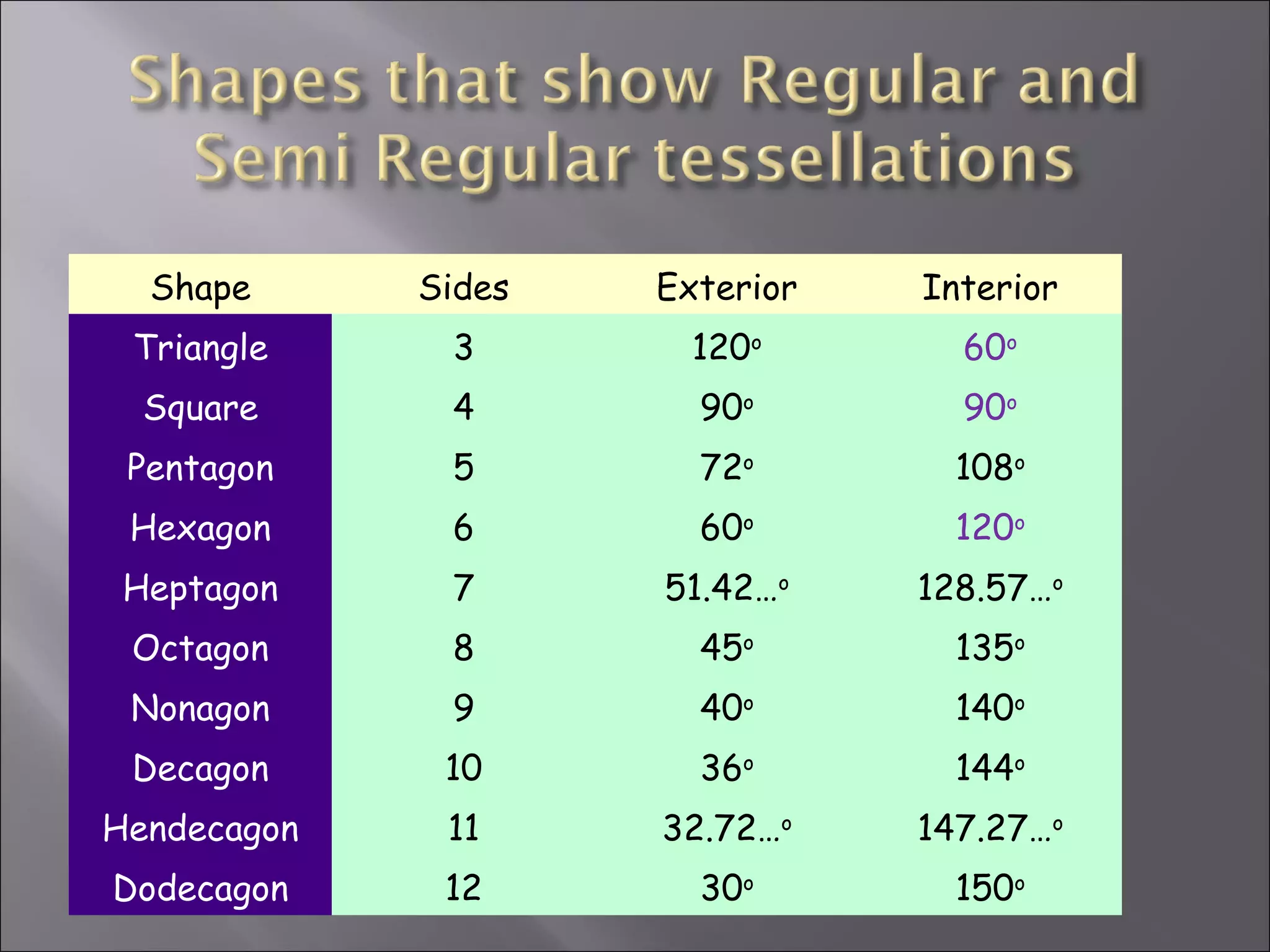
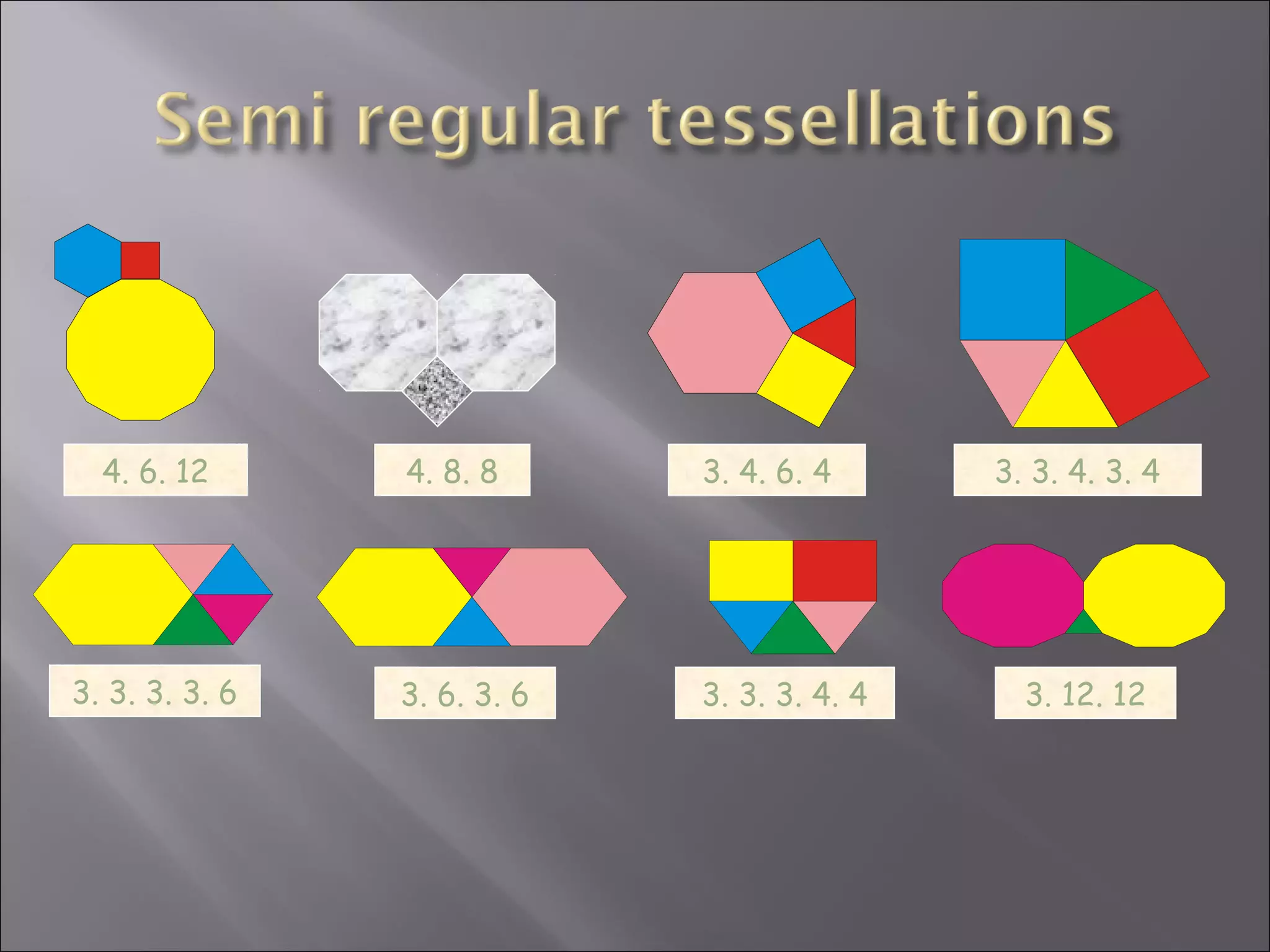
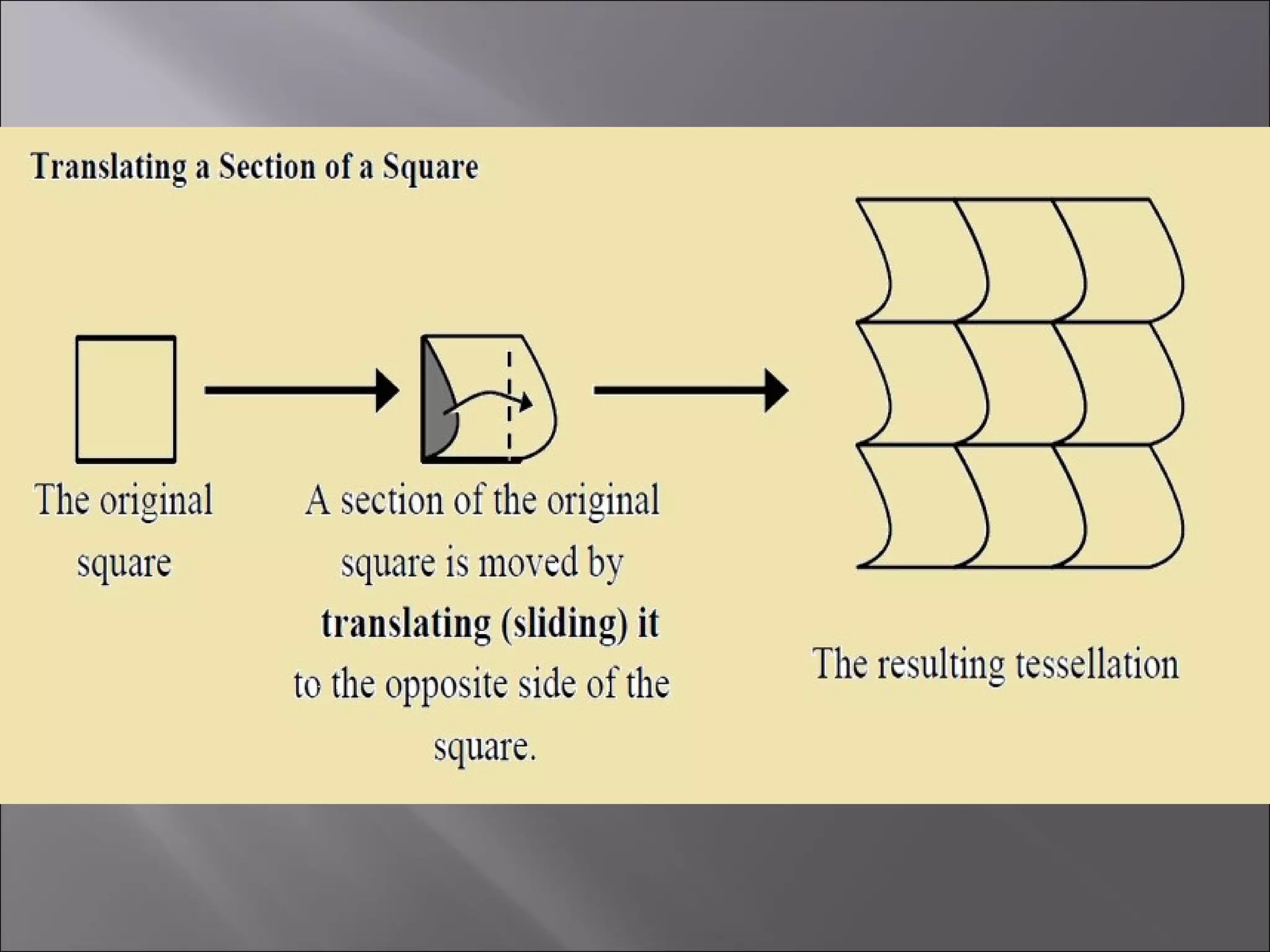
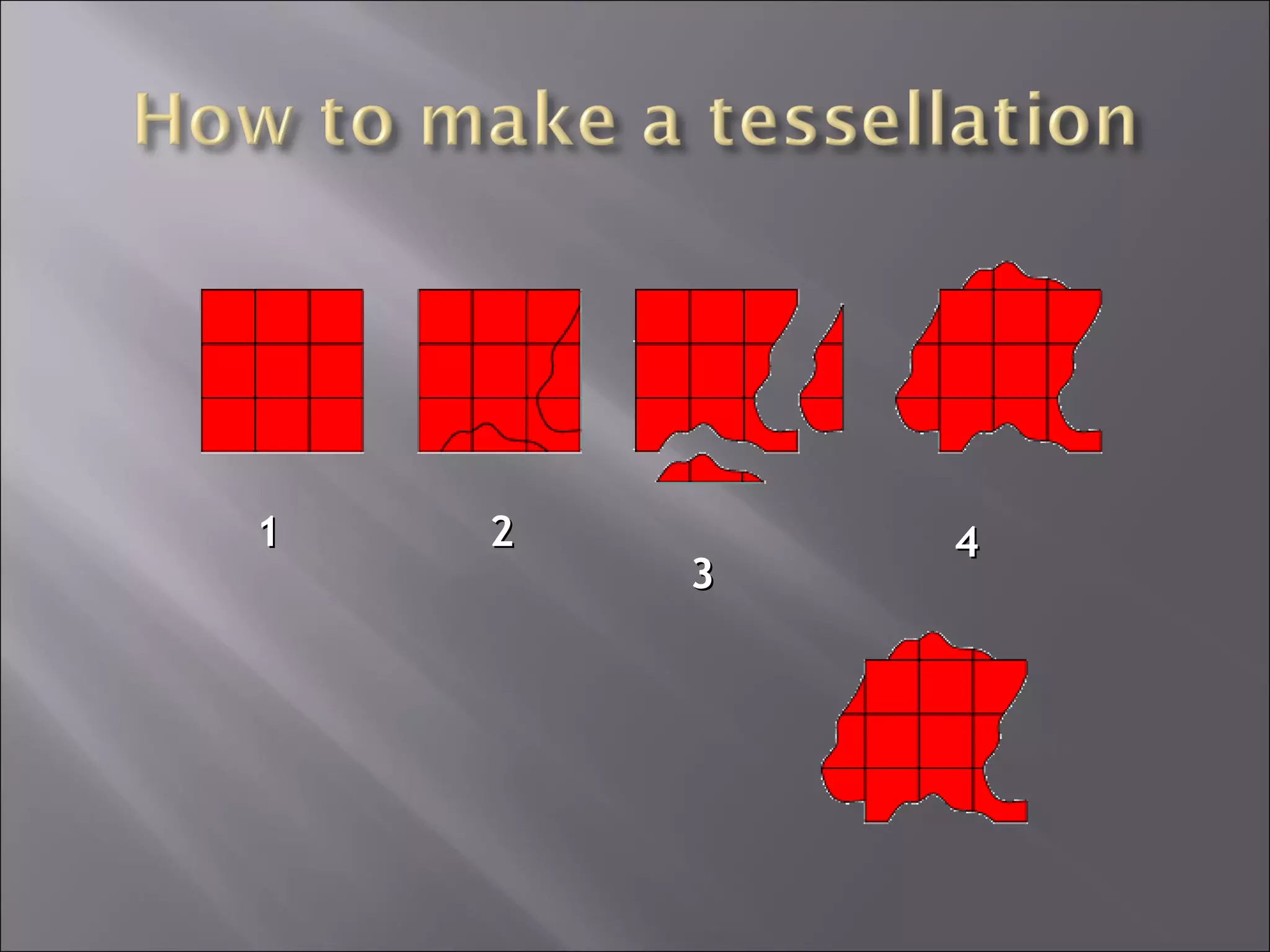
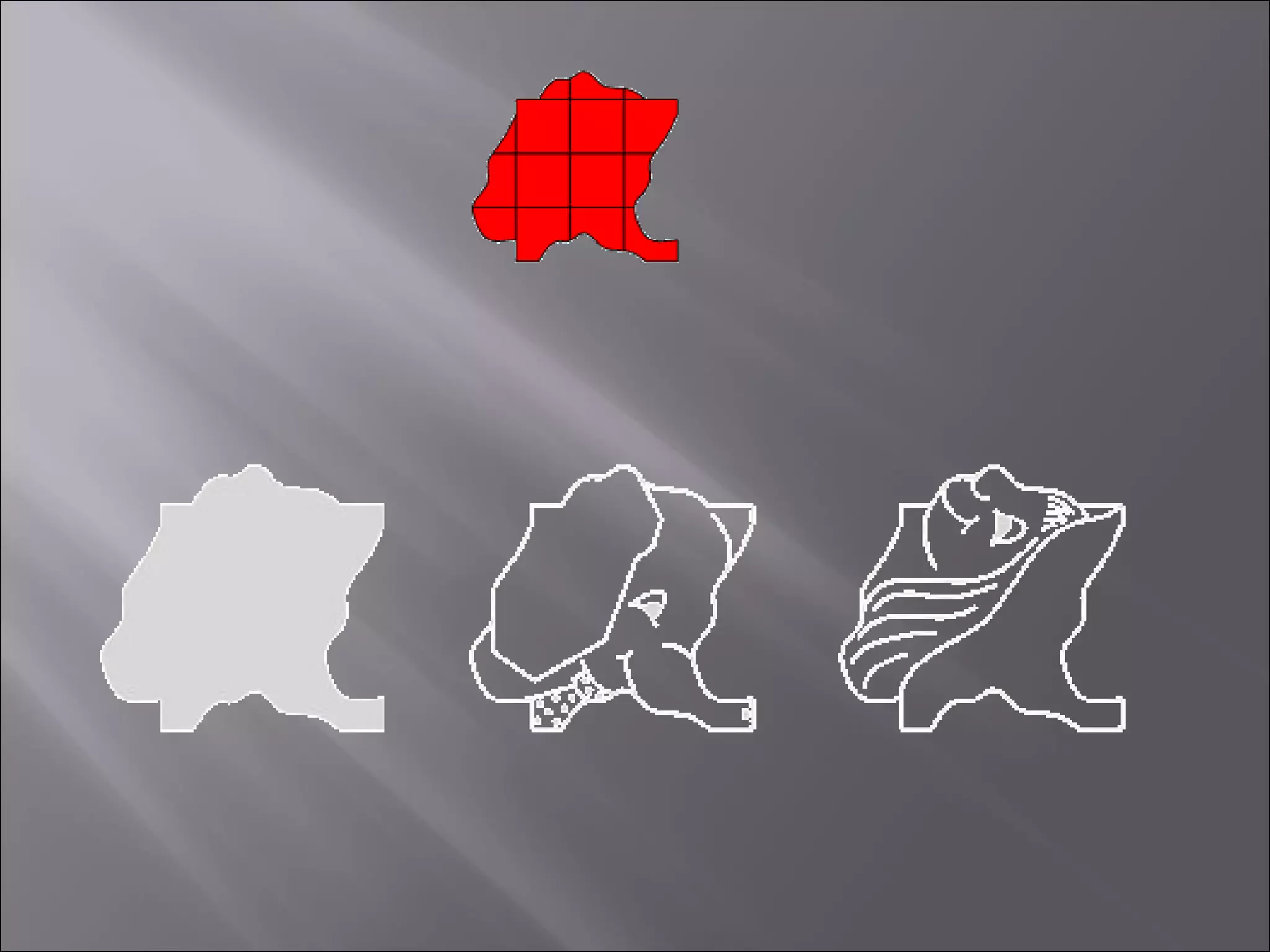
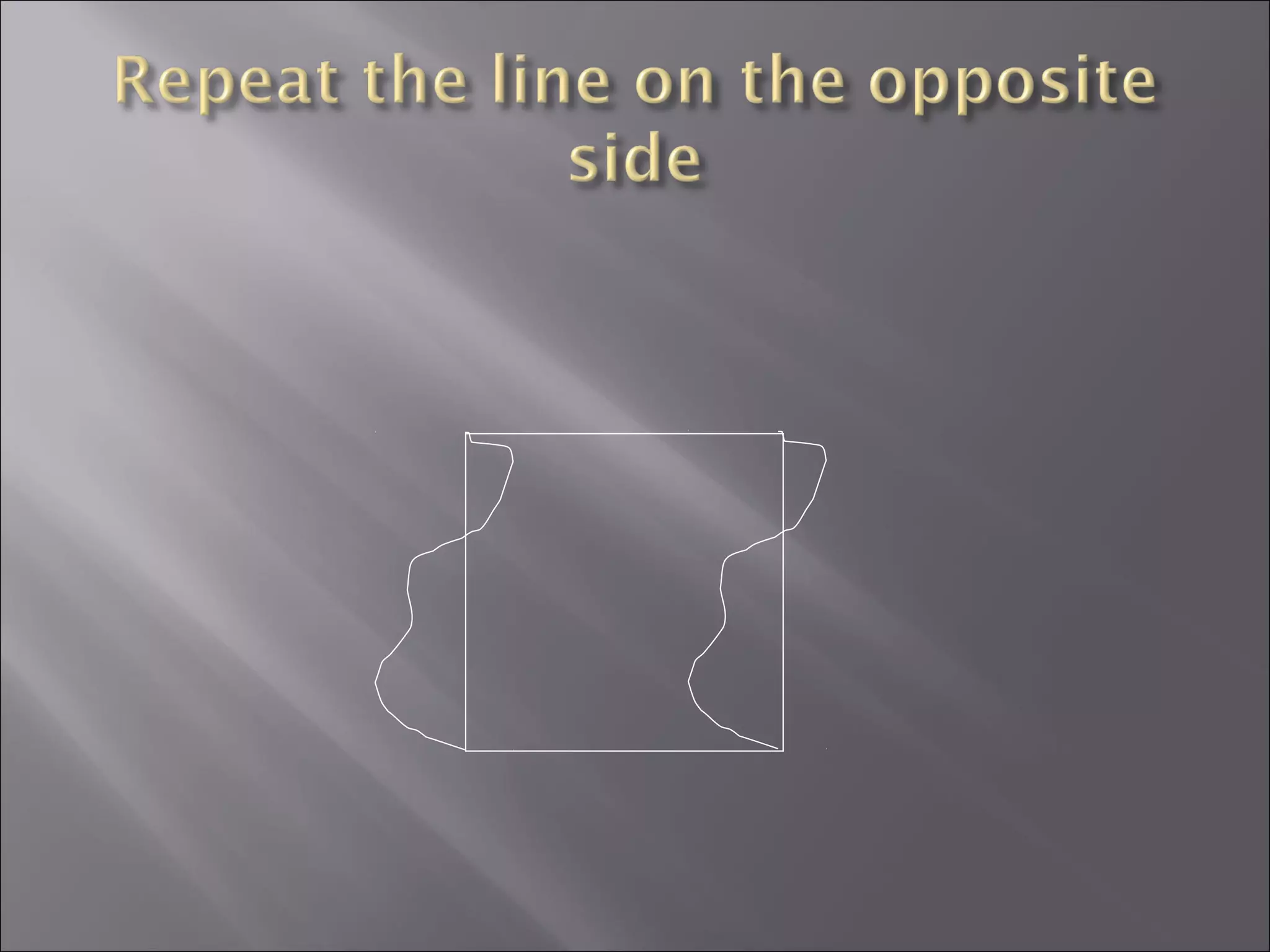
This document discusses tessellations, which are geometric patterns that tile a plane without gaps or overlaps. It provides information on different types of tessellations including regular, semi-regular, and demi-regular tessellations. It also discusses important figures in the history of studying tessellations like Kepler and Fedorov. Examples of tessellations in nature and architecture are given like snake skin, spider webs, honeycombs, Islamic arch designs, and minarets.

2. Roll no : 003

4. What is this???

5.  Many ancient cultures have
used tessellations.
 Johannes Kepler conducted
one of the first
mathematical studies of
tessellations.
 E.S. Fedorov proved an
aspect of tiling in 1891.
 Historically, tessellations were
used in Ancient Rome and in
Islamic art such as in the
decorative tiling of the
Alhambra palace

6. Islamic art does not
usually
use representations of
living
beings, but uses
geometric patterns,
especially symmetric
(repeating) patterns.

8.  “I try in my print to
testify that we live in a
beautiful and orderly
world, not in a chaos
without norms, even
though that is how it
sometimes appears. the
nonsensicalness of some
of what we take to be
irrefutable certainties.”

9.  Most famous creator of
tessellations
 Born in Holland in 1898
(died in 1972)
 Originally studied
architecture before
becoming interested in
woodcuts and printmaking
 Did 137 tessellations in his
lifetime

10. House of Stairs
R
e
p
t
i
l
e
s

11.  Tessellations are
arrangement of shapes
that cover the picture
without overlapping
and without leaving
spaces.
 The word
“tessellation” comes
from the Latin word
“tessera” which means
“small stone cube”
 Tiling is often another
term used for
tessellation patterns.

12. Tessellations around us

13. Formed by
TRANSFORMATION
(combination of
TRANSLATIONS,
ROTATIONS
REFLECTIONS
And
GLIDE REFLECTION)

14. Movements of a figure in a
plane
May be a SLIDE, FLIP, or
TURN

15. Another name for a SLIDE
A
C B
A’
C’ B’
A’, B’ and C’ are explained in the next slide...

16. The figure you get after a
translation
A A’
Slide
C B C’ B’
Original Image
The symbol ‘ is read “prime”.
ABC has been moved to A’B’C’.
A’B’C’ is the image of ABC.

17. Finding the amount of
movement LEFT and RIGHT
and UP and DOWN

18. 9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9
Right 4 (positive change in x)
Down 3
(negative
change in y)
A
A’
B
B’
C
C’

19. Can be written as:
 R4, D3
(Right 4, Down 3)
 (x+4, y-3)

20. Another name for a
FLIP
A A’
C B B’ C’

21.  Used to create
SYMMETRY on the
coordinate plane.
Symmetry
 When one side of
a figure is a
MIRROR IMAGE
of the other

22. Axis of Symmetry is a line that divides the figure into two
symmetrical parts in such a way that the figure on one
side is the mirror image of the figure on the other side
1
2
3
4
1
2
3
4
5
6
1
2
3

23. The line you reflect a figure across.

24.  Another name for a TURN
 A transformation that turns about a fixed point
B
B’
C
C’
A A’

25. The fixed point
(0,0)
A
A’
C
C’
B
B’

26.  When an image after rotation of 180
degrees or less fits exactly on the original.
90 degrees
A
A’
C
C’
B
B’

27. The figure that
results after
reflection and
translation.

28. There are three main types of
tessellations:
 Regular
 Semi-Regular
 Demi-Regular

29.  A regular tessellation is a
pattern only using one regular
polygon shape.
 May also called Pure
Tessellation.
 A regular polygon is any many
sided shape that has sides of
equal length and angles or
equal measure.

30. 3. 3. 3. 3. 3. 3 4. 4. 4. 4 6. 6. 6

33.  Divide the whole turn (360⁰) by the number of
exterior angle (= the number of sides) to find the
size of one exterior angle. Then use the fact that
the exterior angle + the corresponding interior angle
=180⁰

34.  The sum of interior angles of a n-sided regular
polygons { (n-2)⤬180⁰}.
Then the size of one of the interior angle can be
found by dividing by number of interior angle
{=n}.
∠ =(n-2)⤬180⁰ / n

35. Determine whether a regular 6-gon tessellates the plane. Explain?
Let Ð1 represent one interior angle of a regular 4-gon.
m∠1=180⁰(n-2) / n Interior angle theorem
= 180⁰(6-2)/4 Substitution
=180⁰ Simplify
Answer: As 180⁰ is a factor of 360⁰ .so a 6-gon will
tessellate the plane .

36. The sum (total) of the
angles around any Point
is 3 × 120° = 360°.
 This fact is true of
all such points where
the vertices of 3
hexagons meet and thus
the hexagons will
tessellate.

37.  This tessellation may be represented
by the abbreviated notation 6^3
(signifying that three six sided
regular polygons meet at a common
vertex).

38. Determine whether a regular 16-gon tessellates the plane. Explain?
Let Ð1 represent one interior angle of a regular 4-gon.
m∠1=180⁰(n-2) / n Interior angle theorem
= 180⁰(16-2)/4 Substitution
=157.5⁰ Simplify
Answer: As 157.5⁰ is not a factor of 360⁰ .so a 16-gon will not tessellate the plane.

39.  A semi-regular tessellation
is a pattern consisting of
more than one type of
regular polygon.
 The vertex arrangement is
the same throughout the
entire pattern

40. Shape Sides Exterior Interior
Triangle 3 120o 60o
Square 4 90o 90o
Pentagon 5 72o 108o
Hexagon 6 60o 120o
Heptagon 7 51.42…o 128.57…o
Octagon 8 45o 135o
Nonagon 9 40o 140o
Decagon 10 36o 144o
Hendecagon 11 32.72…o 147.27…o
Dodecagon 12 30o 150o

41. 4. 6. 12 4. 8. 8 3. 4. 6. 4 3. 3. 4. 3. 4
3. 3. 3. 3. 6 3. 6. 3. 6 3. 3. 3. 4. 4 3. 12. 12

42. by interior angle theorem …
Octagon has 135 degree
angle of each side…
Square has 90 degree
90⁰+135⁰+135⁰=360⁰

43. Three equilateral triangle and
two square tesselate the
plane…
60⁰+60⁰+60⁰+90⁰+90⁰=360⁰

44.  Determine whether a semi-regular tessellation can be
created from regular nonagons and squares, all having sides
1 unit long.
Each interior angle of a regular nonagon
measures or 140°.
Each angle of a square measures 90°.
Find whole-number values for n and s such that
All whole numbers greater than 3 will result in a negative
value for s.

45. Substitution
Simplify.
Subtract from
each side.
Divide each side
by 90.
Answer: There are no whole number values
for n and s so that

46.  A demi-regular
tessellation is a
pattern of regular
polygons in
which there are
two or three
different polygon
arrangements

47.  Tessellation of an irregular shape can be
obtained by Transformation of other
Tessellating shapes.
 Irregular shapes are those that does not have
all sides and angle equal .

58. 11 22
33
44

61. The metamorphoses consist of
abstract shapes changing into
sharply defined concrete forms,
and then changing back again (a
bird changing into a fish, a lizard
into a honeycomb).

73. The most detailed
shape can be
changed quite a
bit

74. The most
detailed shape
can be changed
quite a bit

80.  Tessellations
can be found
in quilts, floor
tiling, and
wallpaper.

81. snake skin
spider web
Honey comb

83. Islamic Arch
Islamic Minaret