2nd year seminar of Paolo Emidio Sebastiani' Thesis, Ph.D. Student in Structural Engineering, School of Engineering, University of Rome La Sapienza

1. 1
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Ph.D. Student Paolo Emidio Sebastiani Advisors Prof. Franco Bontempi Dr. Francesco Petrini
a.a. 2014/2015 – Seminario intermedio XXVIII Ciclo

2. 2
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
1.1 – TOPICS, KEYWORDS AND TOOLS
 Topics
Seismic vulnerability assessment (design, retrofitting)
Strategic structures: bridges, (demand, performance, capacity, loss)
Seismic retrofitting (aging, life-cycle cost)
Modern technologies (bearings, isolation devices)  Tools
Full probabilistic approach (uncertainties, flexibility)
Finite element modelling (nonlinear analysis, no time consuming)

3. 3
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
1.2 – STATE OF ART AND MOTIVATIONS
 References on lifecycle costs (LCC) and aging
“The time-dependency of risk (seismic) in a lifecycle context is a quite new area to be explored. In seismic analysis, aging consideration has started to be included in seismic performance prediction models” (Decò and Frangopol 2013, Ghosh and Padgett 2010)
Decò A. and Frangopol D.M. (2013). Life-Cycle Risk Assessment of Spatially Distributed Aging Bridges under Seismic and Traffic Hazards. Earthquake Spectra: February 2013, Vol. 29, No. 1, pp. 127-153. Ghosh J. and Padgett J.E. (2010). Aging considerations in the development of time-dependent seismic fragility curves, Journal of Structural Engineering 136, 1497–1511

4. 4
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it
Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
1.3 – FULL PROBABILISTIC APPROACHES IN THE PERFORMANCE-BASED EARTHQUAKE ENGINEERING (PBEE) FRAMEWORK
Franchin P. (2009) Research Within The Framework Of Performance-based Earthquake Engineering, Earthquake Engineering by the Beach Workshop, July 2-4, 2009, Capri, Italy Cornell C.A. and Krawinkler H. (2000). Progress and Challenges in Seismic Performance Assessment. PEER Center News Spring 2000, 3(2).
 Unconditional probabilistic methods
FORM, SORM
Simulation methods (Monte Carlo, Subset Simulation)  Conditional probability methods (IM-based)
SAC/FEMA
PEER method (Cornell, 2000)
random vibration problem
classical structural reliability methods
closed-form
more flexible
decomposition in conditional probabilities
not closed-form

5. 5
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Structural Engineers Assn. of California (SEAOC), (1995) Vision 2000 Committee. April 3, 1995. Performance Based Seismic Engineering of Buildings. J. Soulages, ed. 2 vols. [Sacramento, Calif.] Pinto P.E., Bazzurro P., Elnashai A., Franchin P., Gencturk B., Gunay S., Haukaas T., Mosalam K. & Vamvatsikos, D. (2012). Probabilistic Performance-Based Seismic Design. fib Bulletin 68
1.4 – STATE OF PRACTICE AND MOTIVATIONS
 Italian and european codes
DM 14-01-08, Eurocodes  Other codes
SEAOC Vision 2000 (1995), FEMA273 (1997)
ATC-40 (1989)
 References on PBEE for the state of practice
“The (conditional probability approaches) have a distinct practice-oriented character, they are currently employed as a standard tool in the research community and are expected to gain ever increasing acceptance in professional practice” (Pinto et al., 2012)
Semi-probabilistic approach
Safety coefficient – limit states
Quantifiable confidence
Many performance levels

6. 6
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Cornell C.A. and Krawinkler H. (2000) Progress and Challenges in Seismic Performance Assessment. PEER Center News Spring 2000, 3(2).
1.5 – PEER FORMULATION
 Random variables
Decision Variable DV (repair cost, down time)
Damage Measure DM (cracking)
Engineering Demand Parameter EDP (drift)
Intensity Measure IM (Peak ground acceleration)  Probabilistic models
G(DV|DM) loss or performance model
G(DM|EDP) capacity model
G(EDP|IM) demand model
l(x) mean annual frequency of x

7. 7
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
*
STATE OF ART
1.6 – PEER FRAMEWORK
Krawinkler H. and Miranda E. (2004) Chapter 9: Performance-based earthquake engineering. In: Bertero V.V., Bozorgnia Y.(eds) Earthquake engineering: from engineering seismology to performance-based engineering. CRC Press, Boca Raton

8. 8
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
2.1 – THE CASE STUDY “MALA RIJEKA VIADUCT”

9. 9
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Bridge data
The bridge was built in 1973 as the highest railway bridge in the World
 It has a continuous five-span steel frame carried by six piers of which the middle ones have heights ranging from 50 to 137.5 m
 The main steel truss bridge structure consists in a continuous girder with a total length L=498.80 m. Static truss height is 12.50 m
Andrews M. (2008) Analysis of the Mala Rijeka viaduct. Proceedings of Bridge Engineering 2nd Conference 2008, 16 April 2008, University of Bath, Bath, UK

10. 10
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
2.2 – OTHER SIMILAR CASES
VIADOTTO “RAGO” - A3 SA-RC – MORANO CALABRO (CS) 1969
VIADOTTO “VACALE” - GIOIA TAURO (RC) 2011
VIADOTTO “CATTINARA” CATTINARA (TS) 2005
AUTOSTRADA SALERNO-REGGIO, POLLA (SA) 2006

11. 11
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
VIADOTTO “MUCCIA” ASSE VIARIO MARCHE-UMBRIA (MC)
VIADOTTO “FORNELLO” S.G.C. ORTE-RAVENNA E45 2003
VIADOTTO IALLÀ AUTOSTRADA MONTE BIANCO-AOSTA 1992
VIADOTTO FRAGNETO - S.S. N.95 "DI BRIENZA"(PZ). 1990

12. 12
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
The seismic hazard can be quantified in terms of an intensity measure (IM) which should define the seismic input to the structure.
What is the best IM in case of isolated system?
Does one have hazard data for that IM?
*
3.1 – HAZARD ANALYSIS

13. 13
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 IM selection
Type of variable (scalar, vector)
Nature of variable (structure dependent)
Linear equivalent model to approximate the nonlinear behavior of the structure  Type of isolation
Elastomeric bearings (ERB), Friction pendulum system (FPS)
PGA
Sa(T1)*
* Issue on the evaluation of T1 in case of complex structure with nonlinear devices

14. 14
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Probabilistic Seismic Hazard Analysis (PSHA)
H(a) is the annual probability of exceeding a seismic hazard intensity measure “a” in a given seismic hazard environment
Field E.H., Jordan T.H. and Cornell C.A. (2003) “OpenSHA: A Developing Community-Modeling Environment for Seismic Hazard Analysis”. Seismological Research Letters, 74, no. 4, p. 406-419

15. 15
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Ground Motion selection
Nature of the signal (Simulated, recorded, spectrum-compatible
Elaboration of the signal (bin groups, scaled or unscaled)
Baker, J.W., Lin, T., Shahi, K.S. and Jayaram, N. (2011). New ground motion selection procedures and selected motions for the PEER Transportation Research Program. PEER Report 2011/03, Pacific Earthquake Engineering Research Center, Berkeley, California, USA. 106 pp.
First set 40 recorded GMs, Magnitude = 6 Source-to-site distance = 25 km Range of Sa is between 0 to 0.6 g
Second set 40 recorded GMs, Magnitude =7 Source-to-site distance = 10 km Range of Sa is up to 1.5g

16. 16
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
*
3.2 – STRUCTURAL ANALYSIS
 Inputs
Signals
Hazard curve

17. 17 P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it
Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
λE0 Ets
ft
(U, fpcU)
(c0, fpc)
E0=2fpc/c0
Ep
f Ets y
16.5 m
16.5 m
cross section
of the pier
materials
 Computational F.E. model
 Material and geometric nonlinearities
 Specific elements for device modelling
 Element with fiber section
 Deck mass (120 m for the 3th pier) : 870 kNs2/m
 Pier mass (distributed along the pier) : 7166 kNs2/m

18. 18
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
INITIAL STIFFNESS k1
STRENGTH fy
POST-YIELDING STIFFNESS k2
FPS
k1=75 k2=160000 kN/m
fy=mW= 256.1 kN
k2=W/R=2134.5 kN/m
ERB
k1=10 k2=50200 kN/m
fy= k1dy =301.2 kN
k2=5020 kN/m
 Computational F.E. model
Zhang J. and Huo Y. (2009) Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Engineering Structures, 31, 1648-1660

19. 19
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 EDP selection
Type of EDP
Local
Intermediate
Global  Nonlinear Time-Hystory Analysis  Probabilistic Seismic Demand Model (PSDM)
Stress and strain of concrete and steel
Column moment and curvature (mc)
Pier’s top displacement (dc)
Mosalam K.M. (2012) Probabilistic Performance-based Earthquake Engineering, University of Minho, Guimarães, Portugal, October 3-4, 2012

20. 20
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
NO ISOLATION
FPS

21. 21
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Probabilistic Seismic Demand Model (PSDM) in all cases

22. 22
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
*
3.3 – DAMAGE ANALYSIS
Krawinkler H. and Miranda E. (2004) Chapter 9: Performance-based earthquake engineering. In: Bertero V.V., Bozorgnia Y.(eds) Earthquake engineering: from engineering seismology to performance-based engineering. CRC Press, Boca Raton

23. 23
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
23
SEC 107
SEC 105
SEC 103
SEC 101
 Capacity curves (pushover analysis)
Concrete cracking achievement st = 5.2 N/mm2 is the ultimate tensile strength

24. 24
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
24
SEC 107
SEC 105
SEC 103
SEC 101
 Capacity curves (pushover analysis)
Steel yielding achievement ss = 440 N/mm2 is the steel yield strength

25. 25
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Choi E., DesRoches R., Nielson B. (2004) “Seismic fragility of typical bridges in moderate seismic zones”. EngStruct 2004;26:187
 Limit states definition
 Three damage states DS namely slight, moderate and complete damage are adopted in this study and their concerning limit values are shown above
Through the pushover analysis presented previously, the slight damage has been associated to the achievement of maximum tensile strength of concrete, while the moderate one to the yielding of the steel rebars
A comparison between the values adopted by Choi et al. (2004) and the ductility factors defined in the EC8 for piers, provides the limit values referred to the collapse

26. 26
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Fragility curves

27. 27
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Annual probability of exceeding each damage state
The seismic fragility can be convolved with the seismic hazard in order to assess the annual probability of exceeding each damage state:

28. 28 P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it
Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
PTf푖 = 1 − 1 − PA푖 T
 T-year probability of exceeding each damage state
 T-year probability of exceeding a damage state
 The probability of at least one event that exceeds design limits
during the expected life T (i.e. T=75 years) of the structure is the
complement of the probability that no events occur which exceed
design limits
Padgett J.E., Dennemann K. and Ghosh J. (2010) Risk-based seismic life-cycle cost–benefit
(LCC-B) analysis for bridge retrofit assessment. Structural Safety 2010; 32(3):165–173.

29.  Benefits of isolation devices in terms of probability of damage
29
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
T-YEARS PROBABILITY OF DAMAGE
SLIGHT DAMAGE
MODERATE DAMAGE
NO ISOLATION
23%
1.3%
ERB
7%
0.3%
FPS
3%
0.04%
Sebastiani P.E., Padgett J.E., Petrini F., Bontempi F. (2014) Effectiveness Evaluation of Seismic Protection Devices for Bridges in the PBEE Framework. Proceedings of ASCE-ICVRAM-ISUMA 2014 - second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) Liverpool, 13th-17th July 2014

30. 30
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
* http://peer.berkeley.edu/publications/annual_report/old_ar/year6/yr6_projects/ta1/1222002.html
*
3.4 – LOSS ANALYSIS
 Inputs
T-year probability of exceeding a damage state

31. 31
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Definition of the nominal cost of restoration
Type of repair strategy, nominal cost Ci of restoration  Evaluation of life-cycle costs due to seismic damage
The expected value of the life-cycle costs due to seismic damage in present day dollars can be expressed as follows:
Where j is the damage state, T is the remaining service life of the bridge, Cj is the cost associated with damage state j, and PTfj is the T- year probability of exceeding damage state j
Slight damage
Moderate damage
Complete damage
Repair cost estimate ($)
2.00E05
5.00E05
2.00E06
Wen Y.K. and Kang Y.J. (2001) Minimum building life-cycle cost design criteria. I: methodology. J Struct Eng 2001;127(3):330–7.

32. 32
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Time-dependent fragility curves  Time-dependent mean annual rate of failure
The mean annual rate of failure, li,m(t), due to occurrence of a particular damage state i, can be approximated by the annual probability of damage due to damage state i as
Ghosh J. and Padgett J.E. (2010) Aging considerations in the development of time-dependent seismic fragility curves. Journal of Structural Engineering 2010
Melchers R.E. (1999) Structural Reliability Analysis and Prediction (2nd edn). Wiley: New York
3.5 – AGING IN THE FRAGILITY STEP

33. 33
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Non-homogeneous Poisson process
In probability theory, a counting process is called a non- homogeneous Poisson process with rate l(t) if the following relation holds for
The time between events in a non-homogeneous Poisson process with a time dependent rate can be modeled by an exponential distribution with the cumulative density function (CDF) and the probablity density function (PDF) following the equations
CDF
PDF

34. 34
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Seismic losses corresponding to a damage state i
The present value of total seismic losses corresponding to a damage state i along the service life of the bridge is given by (Beck et al. 2002)
Where d is the discount ratio to convert future costs into present values and T is the service life of the bridge.
The present value of total seismic losses corresponding to a damage state i along the service life of the bridge is given by
Beck J.L., Porter K.A., Shaikhutdinov R.V., Au S.K., Mizukoshi K., Miyamura M. et al. (2002) Impact of seismic risk on lifetime property values. Monograph, Technical Report: CaltechEERL:2002.EERL-2002-04, California Institute of Technology, 2002.
3.6 – AGING IN THE LOSS STEP

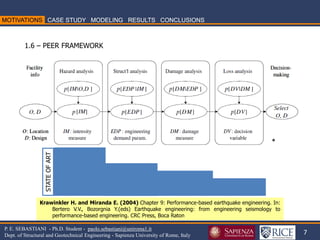
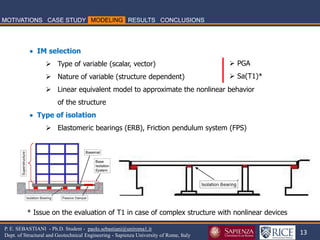
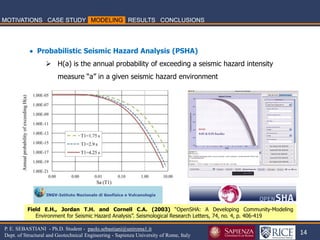
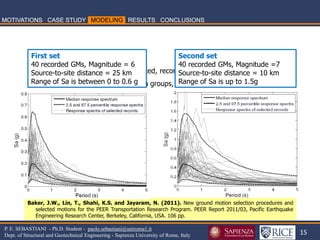
35. 35
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Expected cost value
Moreover the expected value can be evaluated as
Where Ci,m is the nominal cost associated with damage state ith to restore the bridge and P[Ci,m(t)] is the probability of incurring the cost Ci,m
The probability can be approximated by the summation of its PDF values calculated from t=0 to t=T in the discrete space as follows
Ghosh, J. and Padgett, J.E. (2011) Probabilistic seismic loss assessment of aging bridges using a component-level cost estimation approach. Earthquake Engng Struct. Dyn.

36. 36
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Expected cost and variance
Assuming a damage state i, a nominal cost Ci,m=2.0E06 $, a discount factor 0.03, T=75 years
35%

37. 37
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Flowchart of the loss estimation
Rate of failure li,m(t) due to occurrence of a damage state i
Probability of at least one event during {0,t}
Restoration cost Ci,m for the damage state i
Probability of incurring a hypothetical cost Ci,m in {0,t}
Expected seismic loss corresponding to a damage state i during {0,t}
Time-dependent cost C(t) formulation (discount)
Total expected cost across all damage states during {0,t}

38. 38
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
4 – CONCLUSIONS
 Topic
PBEE for loss estimation of isolated bridges with aging effects  Contributions
Application to a real case study, implementing the whole PEER procedure in Matlab environment
Working on a recent formulation to evaluate expected cost and variance in case of aging effects, with a contribution in the discount factor implementation

39. 39
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it
Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
 Works for the next year
Complete results with the full model of the bridge (already done)
Effectiveness evaluation of seismic protection devices in terms of LCC
Application to a second type of more common bridges

40. 40
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy

41. 41
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
PBEE (PEER METHOD)
BRIDGES
ISOLATION
AGING
LCC
PBEE = PERFORMANCE-BASED EARTHQUAKE ENGINEERING LCC = LIFE-CYCLE COST ANALYSIS ISOLATION = SEISMIC ISOLATION SYSTEMS AGING = EFFECTS OF AGING ON THE STRUCTURE
1.7 – TARGET AND CONTRIBUTION

42. 42
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Mosalam K.M. (2012) Probabilistic Performance-based Earthquake Engineering, University of Minho, Guimarães, Portugal, October 3-4, 2012

43. 43
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy

44. 44
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy

45. 45
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy

46. 46
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy

47. 47
P. E. SEBASTIANI - Ph.D. Student - paolo.sebastiani@uniroma1.it Dept. of Structural and Geotechnical Engineering - Sapienza University of Rome, Italy
Ghosh J. and Padgett J.E. (2010) Aging considerations in the development of time-dependent seismic fragility curves. Journal of Structural Engineering 2010