The document discusses various algorithms for searching and sorting data structures. It covers linear search, binary search, insertion sort, selection sort, and bubble sort. For each algorithm, it provides high-level explanations of the approaches and includes pseudocode or code implementations.

1. Chapter Two
Time complexity of known algorithms
•Searching
Linear Search
Binary Search
•Sorting
Insertion Sort
Selection Sort
Bubble Sort
1/12/2023 1

2. Searching: Linear Search
Linear search is a very simple search algorithm. In this type of search, a sequential search is
made over all items one by one. Every item is checked and if a match is found then that
particular item is returned, otherwise the search continues till the end of the data
collection.
Algorithm: Linear Search (Array A, Value x)
• Step 1: Set i to 1
• Step 2: if i > n then go to step 7
• Step 3: if A[i] = x then go to step 6
• Step 4: Set i to i + 1
• Step 5: Go to Step 2
• Step 6: Print Element x Found at index i and go to step 8
• Step 7: Print element not found
• Step 8: Exit
1/12/2023 2

3. The implementation of the algorithm:
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
int main(){
int
array[50],i,target,num;
printf("How many elements
do you want in the array");
scanf("%d",&num);
printf("Enter array
elements:");
for(i=0;i<num;++i)
scanf("%d",&array[i]);
printf("Enter element to search:");
scanf("%d",&target);
for(i=0;i<num;++i)
if(array[i]==target)
break;
if(i<num)
printf("Target element found at location %d",i);
else
printf("Target element not found in an array");
return 0;
}
1/12/2023 3

4. Binary Search
• Binary search is a fast search algorithm with run-time complexity of Ο(log n).
• This search algorithm works on the principle of divide and conquer.
• For this algorithm to work properly, the data collection should be in the sorted form.
• Binary search looks for a particular item by comparing the middle most item of the
collection.
• If a match occurs, then the index of item is returned.
• If the middle item is greater than the item, then the item is searched in the sub-array to
the left of the middle item.
• Otherwise, the item is searched for in the sub-array to the right of the middle item.
• This process continues on the sub-array as well until the size of the subarray reduces to
zero.
1/12/2023 4

5. 1/12/2023 5

6. 1/12/2023 6

7. …cont
1/12/2023 7

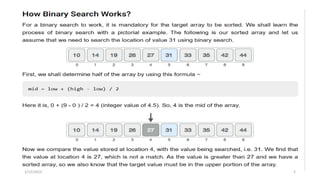
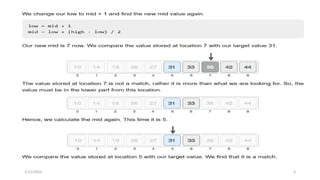
8. Pseudocode
Procedure binary_search:
• A ← sorted array
• n ← size of array
• x ← value to be searched
• Set lowerBound = 1
• Set upperBound = n
• while x not found
• if upperBound < lowerBound
• EXIT: x does not exists.
• set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
• if A[midPoint] < x
• set lowerBound = midPoint + 1
• if A[midPoint] > x
• set upperBound = midPoint - 1
• if A[midPoint] = x
• EXIT: x found at location midPoint
• end while
• end procedure
1/12/2023 8

9. Binary Search Algorithm Implimentation
#include <iostream>
using namespace std;
int binarySearch(int arr[], int left, int right, int x) {
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == x) {
return mid;
}
else if (arr[mid] < x) {
left = mid + 1;
}
else
{
right = mid - 1;
} }
return -1;
}
1/12/2023 9
int main() {
int myarr[10];
int num;
int output;
cout << "Please enter 10 elements ASCENDING order" << endl;
for (int i = 0; i < 10; i++) {
cin >> myarr[i];
}
cout << "Please enter an element to search" << endl;
cin >> num;
output = binarySearch(myarr, 0, 9, num);
if (output == -1) {
cout << "No Match Found" << endl;
} else {
cout << "Match found at position: " << output << endl;
}
return 0;
}

10. Sorting
Insertion Sort: Insertion sort is a sorting algorithm that places an unsorted element at its suitable
place in each iteration.
1. The first element in the array is assumed to be sorted. Take the second
element and store it separately in key.
Compare key with the first element. If the first element is greater than key,
then key is placed in front of the first element.
1/12/2023 10
 Suppose we need to sort the following array.
Initial array

11. … cont
1/12/2023 11

12. … cont
2. Now, the first two elements are sorted.
Take the third element and compare it with the elements on the left
of it. Placed it just behind the element smaller than it. If there is no
element smaller than it, then place it at the beginning of the array.
1/12/2023 12

13. … cont
3. Similarly, place every unsorted element at its correct position
1/12/2023 13

14. Algorithm …
1/12/2023 14

15. Implimentation
// Insertion sort in C++
#include <iostream>
using namespace std;
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
void insertionSort(int array[], int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
1/12/2023 15
// Compare key with each element on the left of
it until an element smaller than // it is found.
// For descending order, change key<array[j] to
key>array[j].
while (key < array[j] && j >= 0) {
array[j + 1] = array[j]; --j;
}
array[j + 1] = key;
} }
// Driver code
int main() {
int data[] = {9, 5, 1, 4, 3};
int size = sizeof(data) / sizeof(data[0]);
insertionSort(data, size);
cout << "Sorted array in ascending order:n";
printArray(data, size);
}

16. Selection Sort
• Selection sort is a sorting algorithm that selects the smallest element
from an unsorted list in each iteration and places that element at the
beginning of the unsorted list.
1. Select first element as minimum
2. Compare minimum with the second element. If the second element is
smaller than minimum, assign the second element as minimum.
Compare minimum with the third element. Again, if the third element is
smaller, then assign minimum to the third element otherwise do nothing. The
process goes on until the last element.
1/12/2023 16

17. … cont
• Compare minimum with the remaining elements
1/12/2023 17

18. … cont
1/12/2023 18

19. … cont
1/12/2023 19

20. Selection Sort
1/12/2023 20

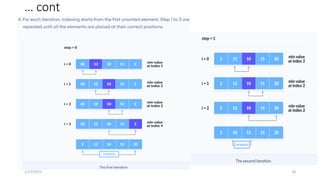
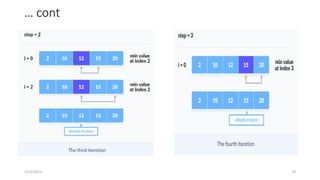
21. Selection Sort Implimentation
// To sort in descending order, change > to <
in this line. // Select the minimum element in
each loop.
if (array[i] < array[min_idx]) min_idx = i;
}
// put min at the correct position
swap(&array[min_idx], &array[step]);
} }
// driver code
int main() {
int data[] = {20, 12, 10, 15, 2};
int size = sizeof(data) / sizeof(data[0]);
selectionSort(data, size);
cout << "Sorted array in Acsending
Order:n";
printArray(data, size);
}
1/12/2023 21
// Selection sort in C++
#include <iostream>
using namespace std;
// function to swap the the position of two elements
void swap(int *a, int *b) {
int temp = *a; *a = *b; *b = temp;
}
// function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
void selectionSort(int array[], int size) {
for (int step = 0;
step < size - 1; step++) {
int min_idx = step;
for (int i = step + 1; i < size; i++) {

22. Bubble Sort
• Bubble sort is a sorting algorithm that compares two adjacent elements
and swaps them until they are in the intended order.
• Suppose we are trying to sort the elements in ascending order.
First Iteration (Compare and Swap)
1. Starting from the first index, compare the first and the second elements.
2. If the first element is greater than the second element, they are
swapped.
3. Now, compare the second and the third elements. Swap them if they are
not in order.
4. The above process goes on until the last element.
1/12/2023 22

23. … cont
1/12/2023 23
2. Remaining Iteration
The same process goes on for the remaining iterations.
After each iteration, the largest element among the
unsorted elements is placed at the end.
Put the largest element at the end

24. … cont
• In each iteration, the comparison takes place up to the last unsorted
element.
• Compare the adjacent elements
• The array is sorted when all the
unsorted elements are placed at
their correct positions.
1/12/2023 24
The array is sorted if all elements
are kept in the right order

25. … cont
1/12/2023 25

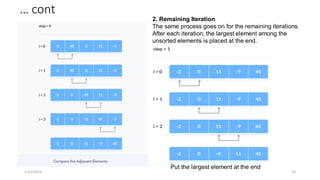
26. Bubble Sort Implementation
// Bubble sort in C++
#include <iostream>
using namespace std;
// perform bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < size; ++step) {
// loop to compare array elements
for (int i = 0; i < size - step; ++i) {
// compare two adjacent elements // change
> to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping elements if elements // are not
in the intended order
int temp = array[i];
array[i] = array[i + 1]; array[i + 1] = temp;
} } } }
// print array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
cout << " " << array[i];
}
cout << "n"; } int main() {
int data[] = {-2, 45, 0, 11, -9};
// find array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
cout << "Sorted Array in Ascending
Order:n";
printArray(data, size);
}
1/12/2023 26

27. Thank You!
?
1/12/2023 27