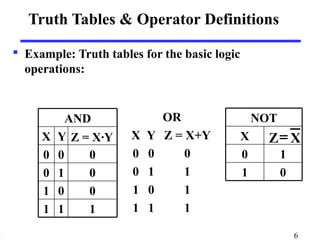
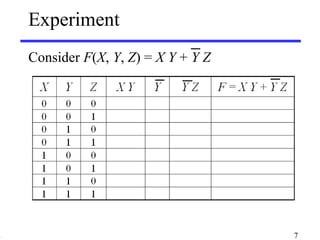
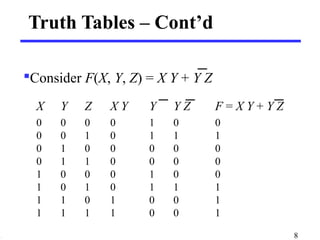
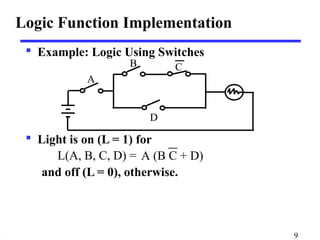
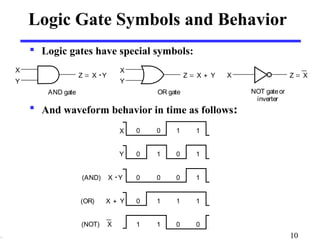
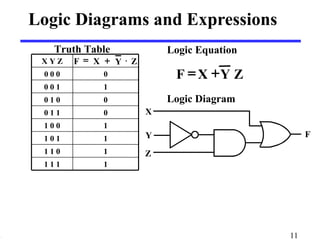
This document discusses logic circuits and how logic expressions are represented using logic gates. It covers basic logical operators like AND, OR, and NOT. Truth tables are used to define the behavior of each logic gate and how they combine input values. Logic functions can be implemented using switches and gates. Diagrams and equations are used to represent complex logic expressions.

1. Logic circuit: logic expression
& its representation using
logic gates
1

2. 2

3. Logic and Gates
 Basic logical operators are the logic functions
AND, OR and NOT.
 Logic gates implement logic functions.
 Boolean Algebra: a useful mathematical system
for specifying and transforming logic functions
to designing and analyzing digital systems!
3

4. Logical Operations
 The three basic logical operations are:
• AND
• OR
• NOT
 AND is denoted by a dot (·).
 OR is denoted by a plus (+).
 NOT is denoted by an over bar ( ¯ ).
4

5. Notation Examples
 Examples:
• Y = A× B
is read “Y is equal to A AND B.”
• z = x + y
is read “z is equal to x OR y.”
• X = A
is read “X is equal to NOT A.”
• 1 + 1 = 2
(read “one plus one equals two”)
• 1 + 1 = 1
(read “1 or 1 equals 1”).
5

6. Truth Tables & Operator Definitions
X
NOT
Z= X
0 1
1 0
 Example: Truth tables for the basic logic
operations:
AND OR
X Y Z = X·Y
0 0 0
0 1 0
1 0 0
1 1 1
X Y Z = X+Y
0 0 0
0 1 1
1 0 1
1 1 1
6

7. Experiment
Consider F(X, Y, Z) = X Y + Y Z
7

8. Truth Tables – Cont’d
Consider F(X, Y, Z) = X Y + Y Z
X Y Z X Y Y Y Z F = X Y + Y Z
0 0 0 0 1 0 0
0 0 1 0 1 1 1
0 1 0 0 0 0 0
0 1 1 0 0 0 0
1 0 0 0 1 0 0
1 0 1 0 1 1 1
1 1 0 1 0 0 1
1 1 1 1 0 0 1
8

9. Logic Function Implementation
 Example: Logic Using Switches
B
A
D
 Light is on (L = 1) for
C
L(A, B, C, D) =
and off (L = 0), otherwise.
A (B C + D)
9

10. Logic Gate Symbols and Behavior
 Logic gates have special symbols:
OR gate
X
Y
Z = X + Y
 And waveform behavior in time as follows:
X 0 0 1 1
Y 0 1 0 1
(AND) X · Y 0 0 0 1
(OR) X + Y 0 1 1 1
(NOT) X 1 1 0 0
X
Y
Z = X · Y
AND gate
X Z = X
NOT gate or
inverter
10

11. Logic Diagrams and Expressions
X
Logic Equation
F = X + Y Z
Logic Diagram
Y F
Z
Truth Table
X Y Z F = X + Y × Z
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
11