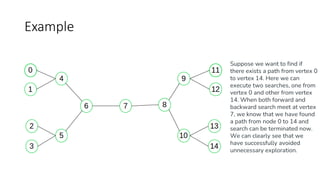
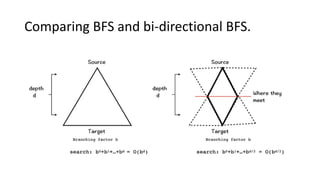
The document outlines an assignment for implementing a bi-directional breadth-first search (BFS) or depth-first search (DFS) to solve navigation problems on a city map represented as a graph. It details the process of simultaneously searching from both source and target nodes to find the shortest path while minimizing node exploration. Key tasks include comparing performance with standard BFS and DFS and visualizing the search process using tools like Python's NetworkX library.

1. Bi-Directional BFS/DFS
Dr Hitesh Mohapatra
Associate Professor
AI-LAB : Assignment 3

2. Assignment 3: Route Finder Using Bi-
Directional BFS/DFS
Objective: Use Bi-directional BFS/DFS to solve a navigation problem.
Problem Statement: Represent a city map as a graph where intersections are
nodes and roads are edges. Find the shortest path between two locations.
Tasks:
• Implement Bi-directional BFS to minimize the number of nodes explored.
• Compare the performance of Bi-directional BFS with standard BFS and
DFS.
• Visualize the search process (e.g., using a library like networkx in Python).

3. What is Bi-Directional BFS?
• Instead of searching from just
the source node, Bi-Directional
BFS searches from both the
start and target.
• The search stops when the two
searches meet in the middle.
• Significantly reduces the
number of nodes explored.

4. Bi-Directional BFS Implementation:
Bi-directional BFS works by simultaneously searching from both the source
and the target nodes. The search meets in the middle, potentially reducing
the number of explored nodes and speeding up the search. This is
particularly effective for large graphs.
Steps for Bi-Directional BFS:
1. Initialize two queues: one starting from the source and the other from
the target.
2. Expand nodes alternately from both ends, marking visited nodes for both
forward and backward searches.
3. If a node is visited by both searches, the algorithm stops, and the path is
reconstructed.

5. Process
It runs two simultaneous search –
1. Forward search from source/initial vertex toward goal vertex
2. Backward search from goal/target vertex toward source
vertex

6. Example
Suppose we want to find if
there exists a path from vertex 0
to vertex 14. Here we can
execute two searches, one from
vertex 0 and other from vertex
14. When both forward and
backward search meet at vertex
7, we know that we have found
a path from node 0 to 14 and
search can be terminated now.
We can clearly see that we
have successfully avoided
unnecessary exploration.

7. When to use bidirectional approach?
We can consider bidirectional approach when-
1. Both initial and goal states are unique and completely
defined.
2. The branching factor is exactly the same in both directions.

8. Algorithm
while sq != empty and tq != empty
perform next iteration for sq
perform next iteration for tq
save the root of a leaf node in the root array
if we have visited the node of intersection
save it
break
using node of intersection and root node, find the path

9. Why bidirectional approach?

10. Comparing BFS and bi-directional BFS.

11. https://github.com/hm18818/AI-with-Python/blob/main/Bi-Directional%20BFS