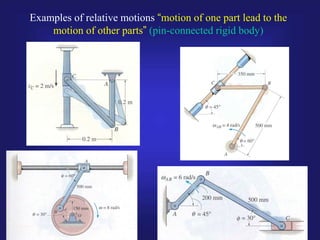
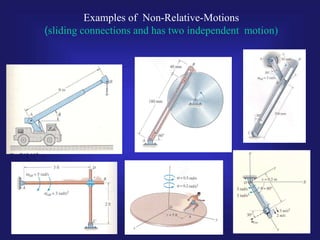
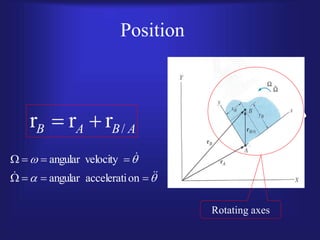
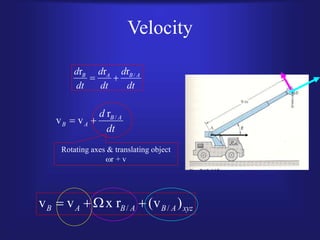
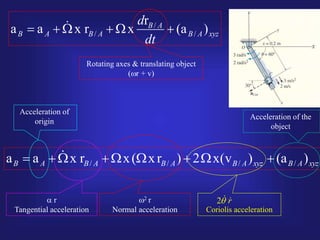
1) The document discusses relative and non-relative motions of connected rigid bodies using examples of pin connections. It defines relative velocity and acceleration and discusses the Coriolis acceleration that arises from rotating frames of reference. 2) An example problem is presented to calculate the relative acceleration of point C with respect to point D, where D is rotating with an angular velocity ω about the z-axis and translating with a velocity v. Expressions are derived for the tangential, normal and Coriolis components of acceleration. 3) The values obtained for this example are aC/D = -6.1 m/s2, ωDE = 3 rad/s, and αDE = -5 rad/s

1. King Fahd University of Petroleum & Minerals
Mechanical Engineering
Dynamics ME 201
BY
Dr. Meyassar N. Al-Haddad
Lecture # 28

2. Examples of relative motions “motion of one part lead to the
motion of other parts” (pin-connected rigid body)

3. Relative-Motion Analysis :
A
B
A
B /
r
x
v
v 


Relative Velocity
A
B
A
B /
2
B/A r
r
a
a 
 



Relative Acceleration
Instantaneous Center of Zero Velocity
IC
B
B /
r

 

4. Examples of Non-Relative-Motions
)sliding connections and has two independent motion)

5. A
B
A
B /
r
r
r 

















on
accelerati
angular
velocity
angular
Position
Rotating axes

6. Velocity
dt
d
dt
d
dt
d A
B
A
B /
r
r
r


dt
d A
B
A
B
/
r
v
v 

xyz
A
B
A
B
A
B )
v
(
r
x
v
v /
/ 



Rotating axes & translating object
r + v

7. Velocity
xyz
O
C
O
C
O
C )
v
(
r
x
v
v /
/ 



VC = Velocity of the Collar, measured from
the X, Y, Z reference
VO = Velocity of the origin O of the x,y,z reference
measured from the X,Y,Z reference
(VC/O)xyz = relative velocity of “C with respect to O”
observer attached to the rotating x,y,z reference
 = angular velocity of the x,y,z reference, measured
from the X,Y,Z reference
rC/O = relative position of “C with respect to O”

8. Acceleration
xyz
A
B
A
B
A
B )
v
(
r
x
v
v /
/ 



dt
d
dt
d
dt
d
dt
dt
d xyz
A
B
A
B
A
B
A
B
)
v
(
r
x
r
x
dv
v /
/
/ 





Acceleration is the time derivative of velocity
xyz
A
B
A
B
A
B
A
B
dt
d
)
a
(
r
x
r
x
a
a /
/
/ 




 
Rotating axes & translating object
(r + v)

9. xyz
A
B
A
B
A
B
A
B
dt
d
)
a
(
r
x
r
x
a
a /
/
/ 




 
Rotating axes & translating object
(r + v)
xyz
A
B
xyz
A
B
A
B
A
B
A
B )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
 r
Tangential acceleration
2 r
Normal acceleration Coriolis acceleration
Acceleration of the
object
Acceleration of
origin
r



2

10. Coriolis acceleration
Whenever a point is moving on a path and the
path is rotating, there is an extra component
of the acceleration due to coupling between
the motion of the point on the path and the
rotation of the path. This component is
called Coriolis acceleration.
First measured by the French engineer G.C. Coriolis
Important in studying the effect “force and acceleration” of earth
rotation on the rockets and long-range projectiles

11. xyz
O
C
xyz
O
C
O
C
O
C
O
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
0
a 
O
2
/ /
4
.
0
)
2
.
0
(
2
x s
m
r
r
a O
C
t 



 

2
2
/
2
/
8
.
1
2
.
0
)
3
(
)
r
x
(
x s
m
r
a O
C
n 




 
2
/ /
3
)
a
( s
m
xyz
O
C 
2
/ /
12
)
2
)(
3
(
2
)
(
x
2
2 s
m
v
r
a xyz
O
C
Cor 



 


2
/
2
.
1
8
.
1
3 s
m
axes
x 



2
/
4
.
12
12
4
.
0 s
m
axes
y 






12. xyz
O
C
xyz
O
C
O
C
O
C
O
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
r
C a
a 
 
a
Recall cylindrical coordinate
2



 r
r
ar 







 r
r
a 2


r
r
r
r
aC






 


 

 2
2
Compare !
Rearrange

13. xyz
O
C
xyz
O
C
O
C
O
C
O
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
xyz
O
C
O
C
O
C )
v
(
r
x
v
v /
/ 



}
k
2
{
}
k
3
{
0
a
0
v









O
O
2
/
/
/
/
}
i
3
{
)
(
/
}
i
2
{
)
v
(
}
i
2
.
0
{
r
s
m
a
s
m
m
rel
O
C
rel
O
C
O
C



i
2
)
i
2
.
0
(
x
)
k
3
(
0
v
)
v
(
r
x
v
v /
/








C
xyz
O
C
O
C
O
C
}
j
6
.
0
i
2
{
v 

C
xyz
O
C
xyz
O
C
O
C
O
C
O
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
i
3
)
i
2
(
x
)
k
3
(
2
)]
i
2
.
0
(
[(-3k)x
x
)
k
3
(
)
i
2
.
0
(
x
)
k
2
(
0
a 







C
2
m/s
12.4j}
-
{1.2i
a
i
3
j
12
i
80
.
1
j
4
.
0
0
a






C
C

14. Recall – Cylindrical coordinate
2



 r
r
ar 







 r
r
a 2


2
2
/
2
.
1
2
.
0
)
3
(
3 s
m
ar 


2
/
4
.
12
)
3
)(
2
(
2
)
2
(
2
.
0 s
m
a 



Coriolis acceleration

15. Example 16-20
xyz
D
C
D
C
D
C )
v
(
r
x
v
v /
/ 



xyz
D
C
xyz
D
C
D
C
D
C
D
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
k
k
0
a
0
v
DE
DE
D
D










 2
/
/
/
/
/
/
i
)
(
/
i
)
v
(
}
i
4
.
0
{
r
s
m
a
a
s
m
m
D
C
xyz
D
C
D
C
xyz
D
C
D
C




s
m
r A
C
AB
C /
}
j
2
.
1
i
2
.
1
{
)
j
4
.
0
i
4
.
0
x(
)
k
3
(
x
v / 





2
2
/
2
/ /
}
j
2
.
5
i
2
{
)
j
4
.
0
i
4
.
0
(
)
3
(
)
j
4
.
0
i
4
.
0
x(
)
k
4
(
x
a s
m
r
r A
C
AB
A
C
AB
C 








 

xyz
D
C
D
C
D
C )
v
(
r
x
v
v /
/ 



i
)
(
)
i
4
.
0
(
x
)
k
(
0
j
2
.
1
i
2
.
1 / xyz
D
C
DE 
 




s
m
xyz
D
C /
2
.
1
)
( / 

s
rad
DE /
3


xyz
D
C
xyz
D
C
D
C
D
C
D
C )
a
(
)
v
(
x
2
)
r
x
(
x
r
x
a
a /
/
/
/ 







 
i
)
i
2
.
1
x(
)
k
3
(
2
)]
i
4
.
0
(
x
)
k
3
[(
x
)
k
3
(
)
i
4
.
0
(
x
)
k
(
0
j
2
.
5
i
2 / D
C
DE a










 
2
/ /
6
.
1 s
m
a D
C  


 2
2
/
5
/
5 s
rad
s
rad
DE

aC/D = ?
DE = ?
DE= ?