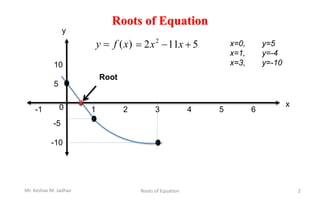
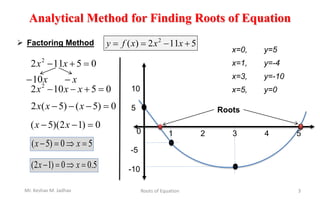
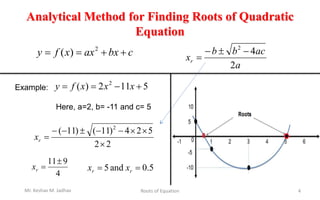
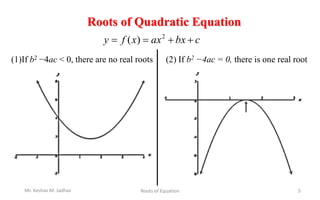
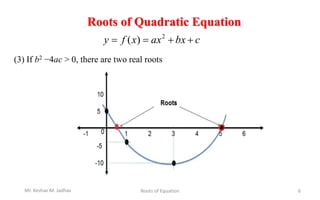
This document discusses methods for finding the roots of equations. It begins by introducing roots of equations and providing examples of roots for simple functions. It then discusses the analytical method for finding roots of quadratic equations using the quadratic formula. The document notes that quadratic equations can have 0, 1, or 2 real roots depending on the discriminant. It also addresses the limitations of analytical methods for more complex algebraic or transcendental equations. Finally, it lists some numerical methods that can be used to find approximations of roots for all types of equations, including the bisection method, regula-falsi method, secant method, and Newton-Raphson method.

1. Mr. Keshav M. Jadhav
Introduction to Roots of
Equation

2. Roots of Equation
2
Roots of Equation
Mr. Keshav M. Jadhav
)
(x
f
y 
1 2 3 4 5 6
-5
-10
0
10
5
-1
Root
x=0, y=5
x=1, y=-4
x=3, y=-10
5
11
2 2


 x
x
x
y

3. Analytical Method for Finding Roots of Equation
3
Roots of Equation
Mr. Keshav M. Jadhav
5
11
2
)
( 2



 x
x
x
f
y
 Factoring Method
0
5
11
2 2


 x
x
0
5
10
2 2



 x
x
x
0
)
5
(
)
5
(
2 


 x
x
x
0
)
1
2
)(
5
( 

 x
x
5
0
)
5
( 


 x
x
5
.
0
0
)
1
2
( 


 x
x
1 2 3 4 5
-5
-10
0
10
5 Roots
x=0, y=5
x=1, y=-4
x=3, y=-10
x=5, y=0
x
x 
10

4. Analytical Method for Finding Roots of Quadratic
Equation
4
Roots of Equation
Mr. Keshav M. Jadhav
5
11
2
)
( 2



 x
x
x
f
y
a
ac
b
b
xr
2
4
2




c
bx
ax
x
f
y 


 2
)
(
Here, a=2, b= -11 and c= 5
Example:
2
2
5
2
4
)
11
(
)
11
( 2









r
x
4
9
11

r
x 5
.
0
and
5 
 r
r x
x

5. Roots of Equation 5
c
bx
ax
x
f
y 


 2
)
(
Roots of Quadratic Equation
(1)If b2 −4ac < 0, there are no real roots (2) If b2 −4ac = 0, there is one real root
Mr. Keshav M. Jadhav

6. Roots of Equation 6
c
bx
ax
x
f
y 


 2
)
(
Roots of Quadratic Equation
(3) If b2 −4ac > 0, there are two real roots
Mr. Keshav M. Jadhav

7. Limitations of Analytical Method for Finding Roots
of Equation
7
Roots of Equation
Mr. Keshav M. Jadhav
Algebraic Equation
900
3632
)
( 5
.
1

 x
x
f
2
5
9
)
( x
x
x
f 

Transcendental Equation
2
2
)
( 

 x
e
x
f x
0
)
log(
)
sin(
5
.
0
)
( 


 x
x
x
x
f 

8. Numerical Methods to Find Root of Algebraic and
Transcendental Equations
1. Bisection Method or Half Interval Method
2. Regula-Falsi Method or False Position Method
3. Secant Method
4. Newton-Raphson Method
5. Successive Approximation Method

9. THANK YOU
9
Roots of Equation
Mr. Keshav M. Jadhav