Download to read offline
Uploaded byssusere0a682
ゲーム理論BASIC 第19回 -有限回繰り返しゲーム-
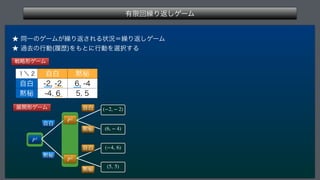
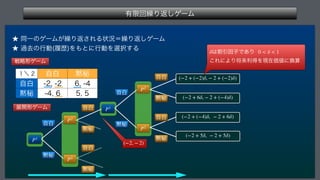
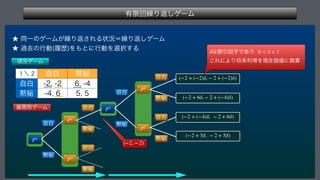
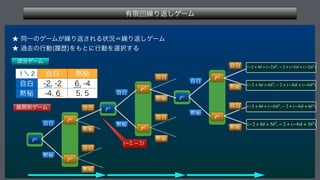
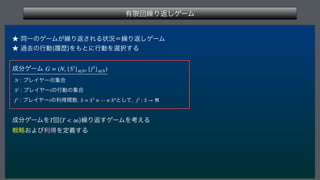
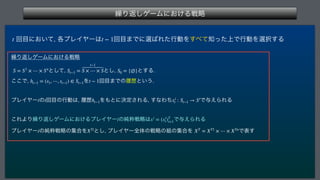
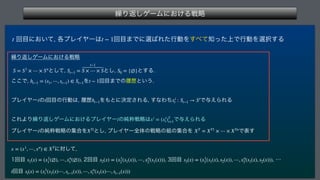
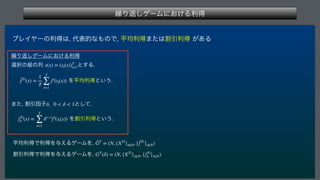
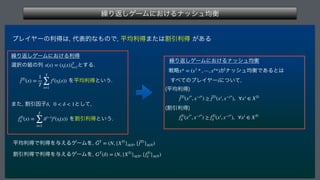
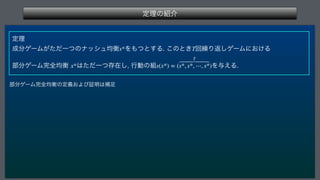
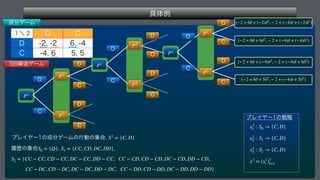
This document describes a finite repeated game model. It defines the game as consisting of a finite number of players N, strategy sets for each player Si, and payoff functions fi for each player. The game is played repeatedly for a finite number of periods T. It also describes how player strategies can change over time based on the history of past play.
More Related Content
ゲーム理論BASIC 第19回 -有限回繰り返しゲーム-
- 1.
- 2. 1. ܁Γฦ͠ήʔϜΛཧղ 2. ܁Γฦ͠ήʔϜͷઓུ རಘΛཧղ ຊಈըͷత
- 3.
- 4.
- 5. ༗ݶճ܁Γฦ͠ήʔϜ ˒ಉҰͷήʔϜ͕܁Γฦ͞ΕΔঢ়܁ʹگΓฦ͠ήʔϜ ˒աڈͷߦಈ ཤྺ ΛͱʹߦಈΛબ͢Δ P1 P2 P2 ࣗന ൿ (−2, − 2) (6,− 4) (−4, 6) (5, 5) ࣗന ൿ ࣗന ൿ ల։ܗήʔϜ ઓུܗήʔϜ ̍ʘ ࣗന ൿ ࣗന ൿ
- 6. ༗ݶճ܁Γฦ͠ήʔϜ ˒ಉҰͷήʔϜ͕܁Γฦ͞ΕΔঢ়܁ʹگΓฦ͠ήʔϜ ˒աڈͷߦಈ ཤྺ ΛͱʹߦಈΛબ͢Δ P1 P2 P2 ࣗന ൿ (−2 + (−2)δ,− 2 + (−2)δ) (−2 + 6δ, − 2 + (−4)δ) (−2 + (−4)δ, − 2 + 6δ) (−2 + 5δ, − 2 + 5δ) ࣗന ൿ ࣗന ൿ ̍ʘ ࣗന ൿ ࣗന ൿ ల։ܗήʔϜ ઓུܗήʔϜ P1 P2 P2 ࣗന ൿ ࣗന ൿ ࣗന ൿ (−2, − 2) ׂҾҼࢠͰ͋Γ ͜ΕʹΑΓকདྷརಘΛࡏݱՁʹࢉ δ 0 δ 1
- 7. ༗ݶճ܁Γฦ͠ήʔϜ ˒ಉҰͷήʔϜ͕܁Γฦ͞ΕΔঢ়܁ʹگΓฦ͠ήʔϜ ˒աڈͷߦಈ ཤྺ ΛͱʹߦಈΛબ͢Δ P1 P2 P2 ࣗന ൿ (−2 + (−2)δ,− 2 + (−2)δ) (−2 + 6δ, − 2 + (−4)δ) (−2 + (−4)δ, − 2 + 6δ) (−2 + 5δ, − 2 + 5δ) ࣗന ൿ ࣗന ൿ ̍ʘ ࣗന ൿ ࣗന ൿ ల։ܗήʔϜ ઓུܗήʔϜ P1 P2 P2 ࣗന ൿ ࣗന ൿ ࣗന ൿ (−2, − 2) ήʔϜ ׂҾҼࢠͰ͋Γ ͜ΕʹΑΓকདྷརಘΛࡏݱՁʹࢉ δ 0 δ 1
- 8. ༗ݶճ܁Γฦ͠ήʔϜ ˒ಉҰͷήʔϜ͕܁Γฦ͞ΕΔঢ়܁ʹگΓฦ͠ήʔϜ ˒աڈͷߦಈ ཤྺ ΛͱʹߦಈΛબ͢Δ P1 P2 P2 ࣗന ൿ ࣗന ൿ ࣗന ൿ ̍ʘ ࣗന ൿ ࣗന ൿ ల։ܗήʔϜ ઓུܗήʔϜ P1 P2 P2 ࣗന ൿ ࣗന ൿ ࣗന ൿ (−2, − 2) ήʔϜ P1 P2 P2 ࣗന ൿ ࣗന ൿ ࣗന ൿ (−2 + 6δ + (−2)δ2 , − 2 + (−4)δ + (−2)δ2 ) (−2 + 6δ + 6δ2 , − 2 + (−4)δ + (−4)δ2 ) (−2 + 6δ + (−4)δ2 , − 2 + (−4)δ + 6δ2 ) (−2 + 6δ + 5δ2 , − 2 + (−4)δ + 5δ2 )
- 9. ༗ݶճ܁Γฦ͠ήʔϜ ˒ಉҰͷήʔϜ͕܁Γฦ͞ΕΔঢ়܁ʹگΓฦ͠ήʔϜ ˒աڈͷߦಈ ཤྺ ΛͱʹߦಈΛબ͢Δ ήʔϜ ϓϨΠϠʔͷू߹ ϓϨΠϠʔͷߦಈͷू߹ ϓϨΠϠʔͷརಘؔ ͱͯ͠ ήʔϜΛ ճ ܁Γฦ͢ήʔϜΛߟ͑Δ ઓུ͓ΑͼརಘΛఆٛ͢Δ G = (N, {Si }i∈N, {fi }i∈N) N Si i fi i S = S1 × ⋯ × Sn fi : S → ℜ T T ∞
- 10. ܁Γฦ͠ήʔϜʹ͓͚Δઓུ ճʹ͓͍ͯ ֤ϓϨΠϠʔ ճ·ͰʹબΕͨߦಈΛ্ͯͬͨ͢ͰߦಈΛબ͢Δ ܁Γฦ͠ήʔϜʹ͓͚Δઓུ ͱͯ͠ ͱ͠ ͱ͢Δ ͜͜Ͱ Λ ճ·Ͱͷཤྺͱ͍͏ ϓϨΠϠʔͷճͷߦಈ ཤྺ Λͱʹܾఆ͞ΕΔ ͢ͳΘͪ Ͱ༩͑ΒΕΔ ͜ΕΑΓ܁Γฦ͠ήʔϜʹ͓͚ΔϓϨΠϠʔͷ७ਮઓུ Ͱ༩͑ΒΕΔ ϓϨΠϠʔͷ७ਮઓུͷू߹Λ ͱ͠ ϓϨΠϠʔશମͷઓུͷͷू߹Λ Ͱද͢ t t − 1 S = S1 × ⋯ × Sn St−1 = t−1 S × ⋯ × S S0 = {∅} ht−1 = (s1, ⋯, st−1) ∈ St−1 t − 1 i t ht−1 xi t : St−1 → Si i xi = (xi t)T t=1 i XTi XT = XT1 × ⋯ × XTn
- 11. ܁Γฦ͠ήʔϜʹ͓͚Δઓུ ճʹ͓͍ͯ ֤ϓϨΠϠʔ ճ·ͰʹબΕͨߦಈΛ্ͯͬͨ͢ͰߦಈΛબ͢Δ ܁Γฦ͠ήʔϜʹ͓͚Δઓུ ͱͯ͠ ͱ͠ ͱ͢Δ ͜͜Ͱ Λ ճ·Ͱͷཤྺͱ͍͏ ϓϨΠϠʔͷճͷߦಈ ཤྺ Λͱʹܾఆ͞ΕΔ ͢ͳΘͪ Ͱ༩͑ΒΕΔ ͜ΕΑΓ܁Γฦ͠ήʔϜʹ͓͚ΔϓϨΠϠʔͷ७ਮઓུ Ͱ༩͑ΒΕΔ ϓϨΠϠʔͷ७ਮઓུͷू߹Λ ͱ͠ ϓϨΠϠʔશମͷઓུͷͷू߹Λ Ͱද͢ ʹରͯ͠ ճ ճ ճ ʜ ճ t t − 1 S = S1 × ⋯ × Sn St−1 = t−1 S × ⋯ × S S0 = {∅} ht−1 = (s1, ⋯, st−1) ∈ St−1 t − 1 i t ht−1 xi t : St−1 → Si i xi = (xi t)T t=1 i XTi XT = XT1 × ⋯ × XTn x = (x1 , ⋯, xn ) ∈ XT s1(x) = (x1 1(∅), ⋯, xn 1(∅)) s2(x) = (x1 2(s1(x)), ⋯, xn 2(s1(x))) s3(x) = (x1 3(s1(x), s2(x)), ⋯, xn 3(s1(x), s2(x))) t st(x) = (x1 t (s1(x)⋯, st−1(x)), ⋯, xn t (s1(x)⋯, st−1(x)))
- 12. ܁Γฦ͠ήʔϜʹ͓͚Δརಘ ϓϨΠϠʔͷརಘ දతͳͷͰ ฏۉརಘ·ׂͨҾརಘ͕͋Δ ܁Γฦ͠ήʔϜʹ͓͚Δརಘ બͷͷྻ ͱ͢Δ Λฏۉརಘͱ͍͏ ·ͨ ׂҾҼࢠͱͯ͠ ΛׂҾརಘͱ͍͏ ฏۉརಘͰརಘΛ༩͑ΔήʔϜΛ ׂҾརಘͰརಘΛ༩͑ΔήʔϜΛ s(x) = (st(x))T t=1 ¯ fTi (x) = 1 T T ∑ t=1 fi (st(x)) δ, 0 δ 1 fTi δ (x) = T ∑ t=1 δt−1 fi (st(x)) ḠT = (N, {XTi }i∈N, {¯ fTi }i∈N) GT (δ) = (N, {XTi }i∈N, {fTi δ }i∈N)
- 13. ܁Γฦ͠ήʔϜʹ͓͚Δφογϡߧۉ ϓϨΠϠʔͷརಘ දతͳͷͰ ฏۉརಘ·ׂͨҾརಘ͕͋Δ ܁Γฦ͠ήʔϜʹ͓͚Δརಘ બͷͷྻ ͱ͢Δ Λฏۉརಘͱ͍͏ ·ͨ ׂҾҼࢠͱͯ͠ ΛׂҾརಘͱ͍͏ ฏۉརಘͰརಘΛ༩͑ΔήʔϜΛ ׂҾརಘͰརಘΛ༩͑ΔήʔϜΛ s(x) = (st(x))T t=1 ¯ fTi (x) = 1 T T ∑ t=1 fi (st(x)) δ, 0 δ 1 fTi δ (x) = T ∑ t=1 δt−1 fi (st(x)) ḠT = (N, {XTi }i∈N, {¯ fTi }i∈N) GT (δ) = (N, {XTi }i∈N, {fTi δ }i∈N) ܁Γฦ͠ήʔϜʹ͓͚Δφογϡߧۉ ઓུ ͕φογϡ͋ͰߧۉΔͱ ͯ͢ͷϓϨΠϠʔʹ͍ͭͯ ฏۉརಘ ׂҾརಘ x* = (x1 * , ⋯, xn *) i ¯ fTi (xi* , x−i* ) ≥ ¯ fTi (xi , x−i* ), ∀xi ∈ XTi fTi δ (xi* , x−i* ) ≥ fTi δ (xi , x−i* ), ∀xi ∈ XTi
- 14. ఆཧͷհ ఆཧ ήʔϜ͕ͨͩҰͭͷφογϡߧۉ Λͭͱ͢Δ͜ͷͱ͖ ճ܁Γฦ͠ήʔϜʹ͓͚Δ ෦ήʔϜશߧۉͨͩҰͭଘࡏ͠ ߦಈͷ Λ༩͑Δ ෦ήʔϜશߧۉͷఆ͓ٛΑͼূ໌ิ s* T x* s(x*) = ( T s*, s*, ⋯, s*)
- 15. ۩ମྫ ϓϨΠϠʔͷήʔϜͷߦಈͷू߹ ཤྺͷू߹ S1 = {C, D} S0 = {∅} S1 = {CC, CD, DC, DD} S2 = {CC − CC, CD − CC, DC − CC, DD − CC, CC − CD, CD − CD, DC − CD, DD − CD, CC − DC, CD − DC, DC − DC, DD − DC, CC − DD, CD − DD, DC − DD, DD − DD} P1 P2 P2 % $ % $ % $ ̍ʘ % $ % $ ճ܁ฦήʔϜ P1 P2 P2 % $ % $ % $ ήʔϜ P1 P2 P2 (−2 + 6δ + (−2)δ2 , − 2 + (−4)δ + (−2)δ2 ) (−2 + 6δ + 6δ2 , − 2 + (−4)δ + (−4)δ2 ) (−2 + 6δ + (−4)δ2 , − 2 + (−4)δ + 6δ2 ) (−2 + 6δ + 5δ2 , − 2 + (−4)δ + 5δ2 ) % $ % $ % $ ϓϨΠϠʔͷઓུ x1 1 : S0 → {C, D} x1 2 : S1 → {C, D} x1 3 : S2 → {C, D} x1 = (x1 t )3 t=1
- 16.