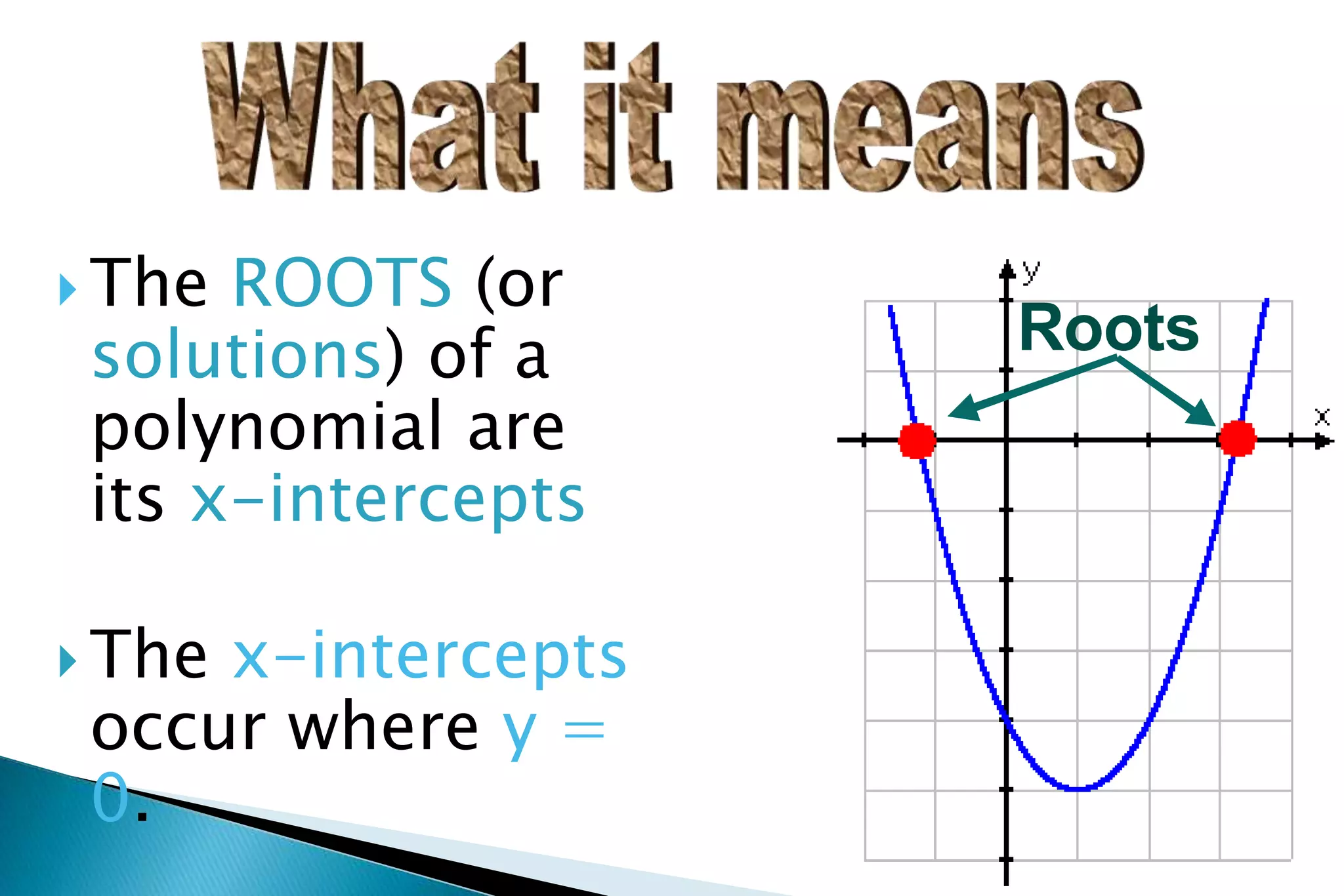
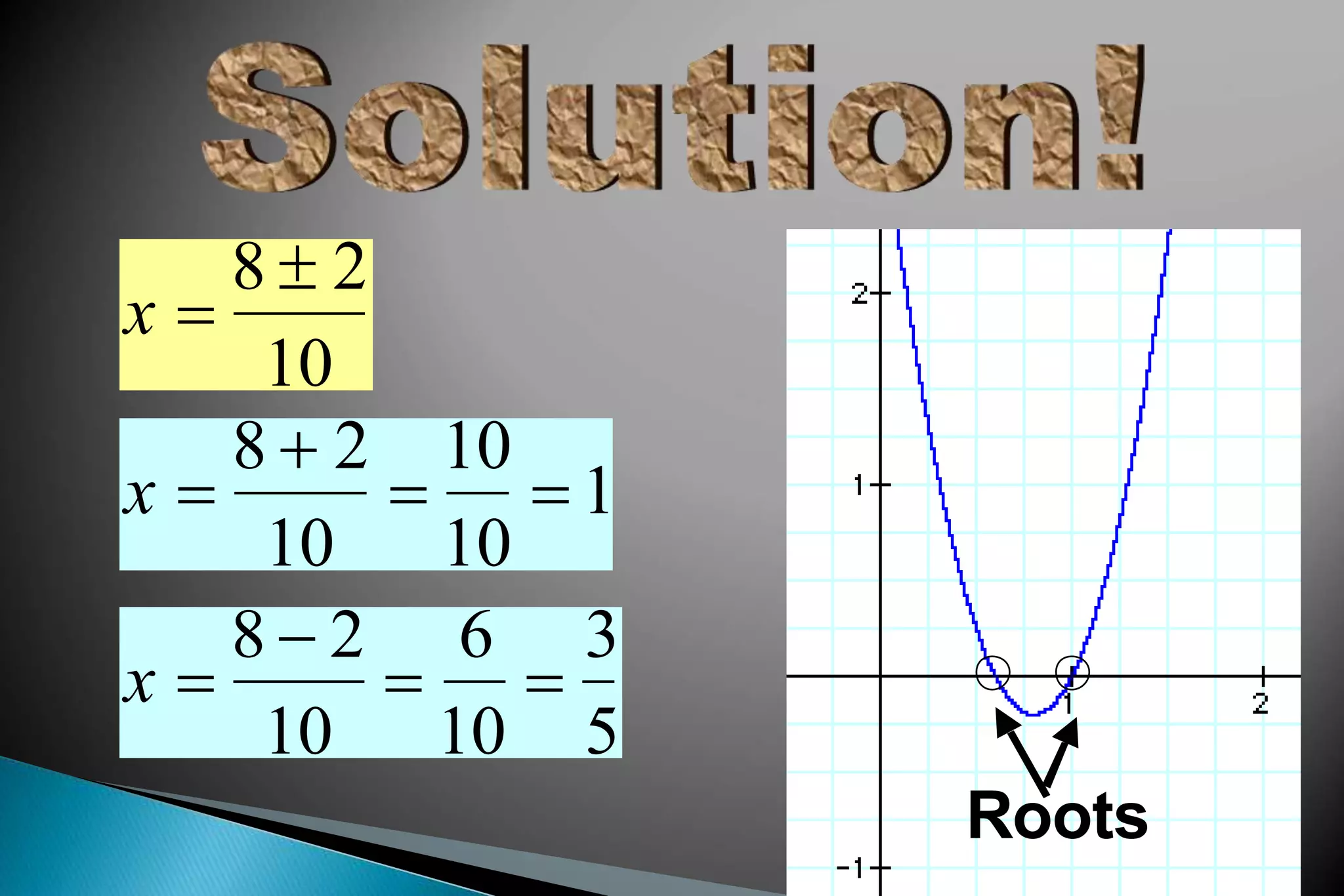
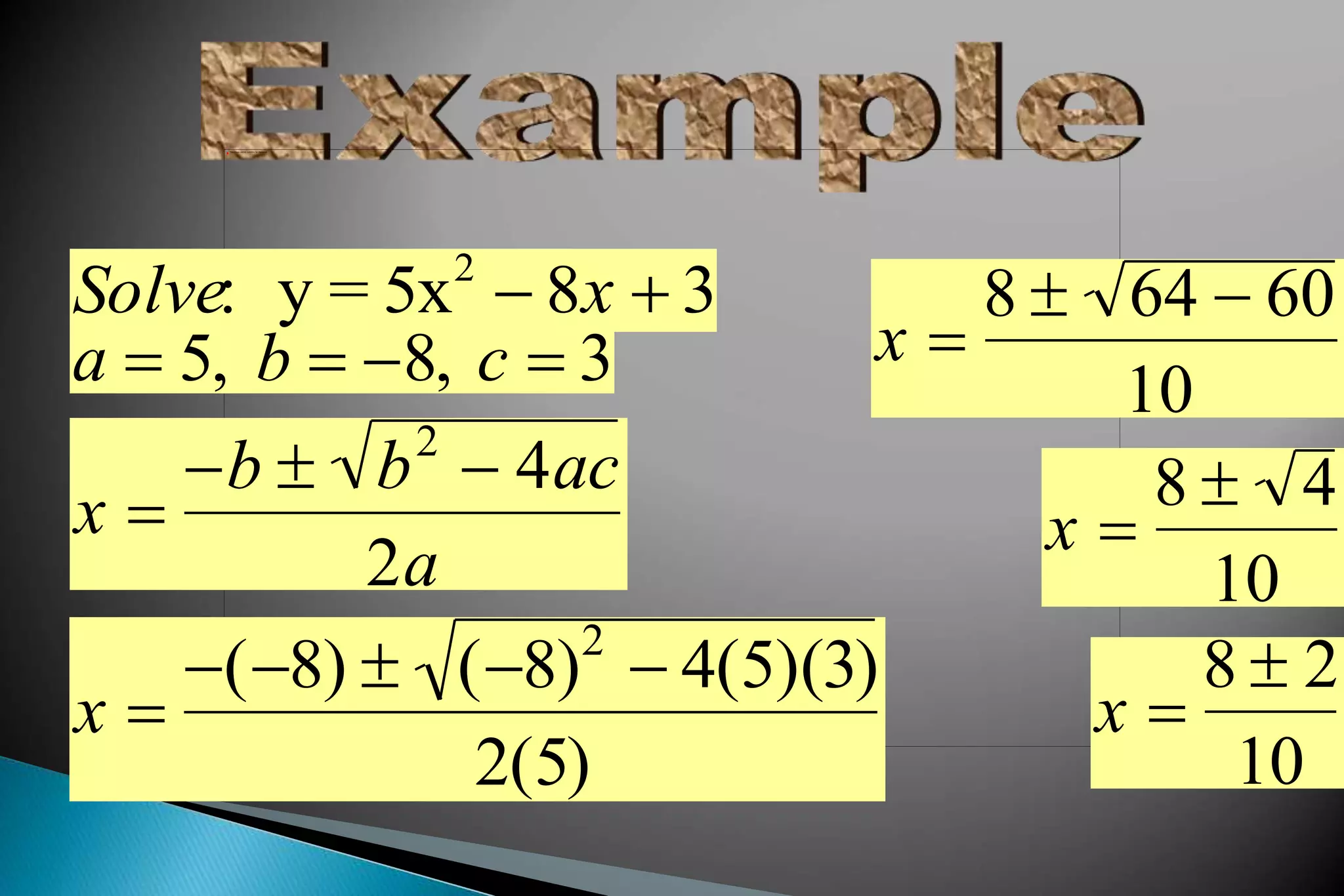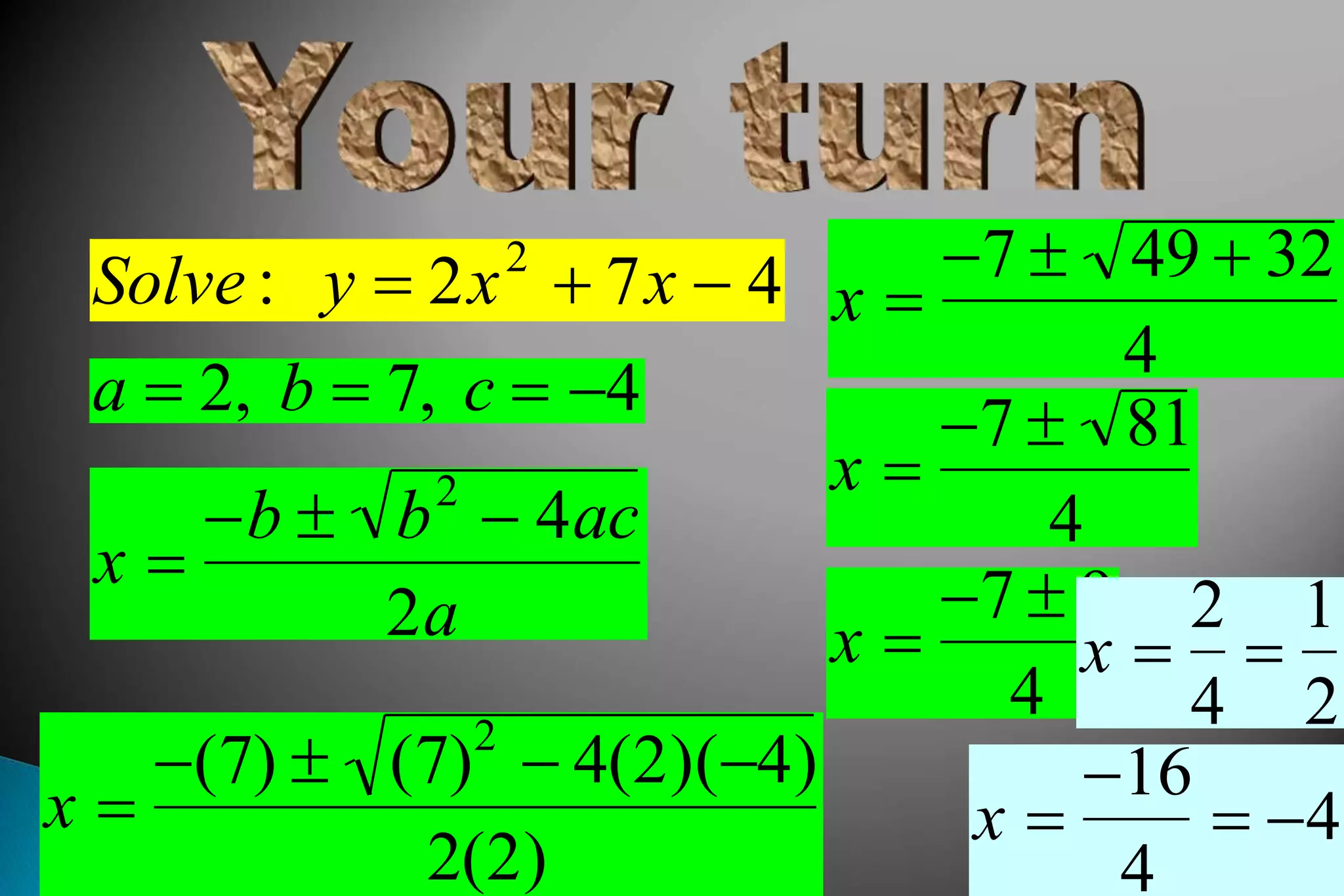The document discusses the quadratic formula and how it can be used to find the roots or solutions of a quadratic equation, even if the equation cannot be factored. It provides the standard form of a quadratic equation as y = ax2 + bx + c and explains that the roots are the x-intercepts where y = 0. Several examples are shown of using the quadratic formula to calculate the roots of quadratic equations by determining the coefficients a, b, and c and plugging them into the formula. The key steps and uses of the quadratic formula are emphasized.

1.  Intro: We already know the
standard form of a quadratic
equation is:
y = ax2 + bx + c
 The coefficients are: a , b, c
 The variables are: y, x

2.  The ROOTS (or
solutions) of a
polynomial are
its x-intercepts
 The x-intercepts
occur where y =
0.
Roots

3.  Example: Find the
roots: y = x2 + x - 6
 Solution: Factoring:
y = (x + 3)(x - 2)
 0 = (x + 3)(x - 2)
 The roots are:
 x = -3; x = 2
Roots

4.  After centuries of
work,
mathematicians
realized that as long
as you know the
coefficients, you can
find the roots of the
quadratic. Even if it
doesn’t factor!
y  ax2
 bx  c, a  0
x 
b  b2
 4ac
2a

5. Solve: y = 5x2
 8x  3
x 
b  b2
 4ac
2a
a  5, b  8, c  3
x 
(8)  (8)2
 4(5)(3)
2(5)
x 
8  64  60
10
x 
8  4
10
x 
8  2
10

6. x 
8  2
10
x 
8  2
10

10
10
 1
x 
8  2
10

6
10

3
5
Roots

7. y  5(1)2
 8(1)  3
y  5 8  3
y  0
y  5 3
5
 
2
 8 3
5
  3
y  5 9
25
  24
5
 3
y  45
25
  24
5
  3
y  9
5
  24
5
  15
5
 
y  0
Plug in your
answers for x.
If you’re right,
you’ll get y = 0.

8. Solve : y  2x2
 7x  4
a  2, b  7, c  4
x 
b  b2
 4ac
2a
x 
(7)  (7)2
 4(2)(4)
2(2)
x 
7  49  32
4
x 
7  81
4
x 
7  9
4
x 
2
4

1
2
x 
16
4
 4

9. Remember: All the terms must be on one
side BEFORE you use the quadratic
formula.
•Example: Solve 3m2 - 8 = 10m
•Solution: 3m2 - 10m - 8 = 0
•a = 3, b = -10, c = -8

10.  Solve: 3x2 = 7 - 2x
 Solution: 3x2 + 2x - 7 =
0
 a = 3, b = 2, c = -7
x 
b  b2
 4ac
2a
x 
(2)  (2)2
 4(3)(7)
2(3)
x 
2  4  84
6
x 
2  88
6
x 
2  4• 22
6
x 
2  2 22
6
x 
1 22
3

11.  Watch this:
http://www.youtube.com/watch?v=jGJrH49Z2ZA
THANKS!!!