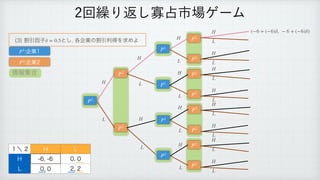
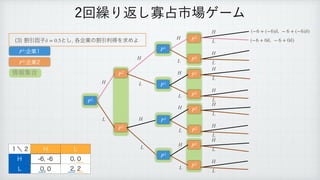
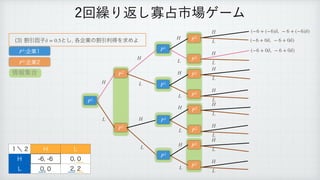
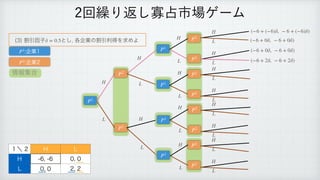
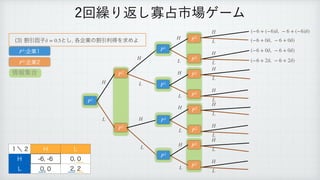
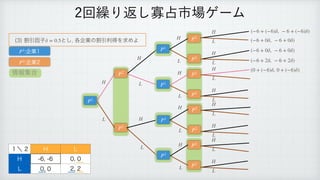
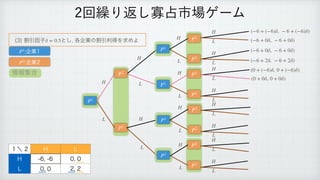
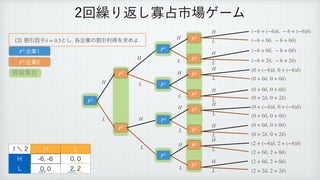
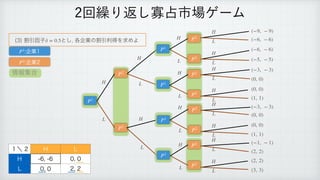
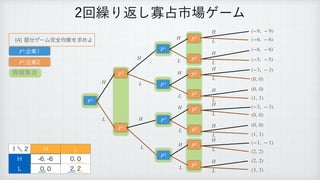
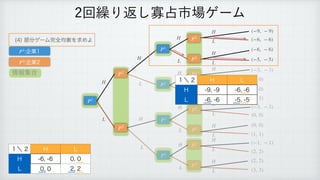
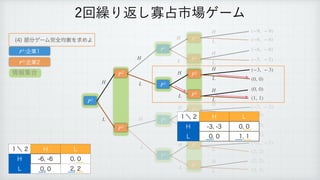
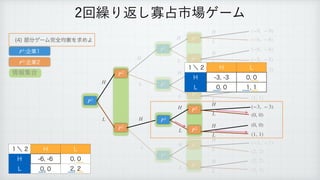
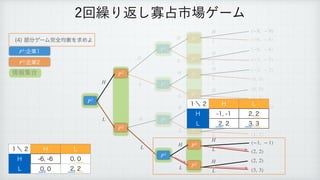
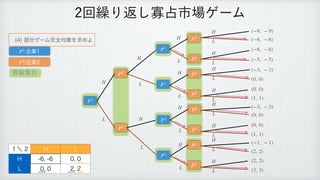
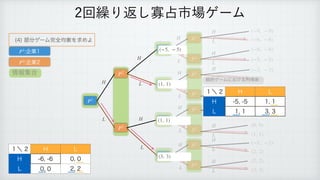
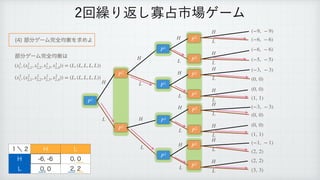
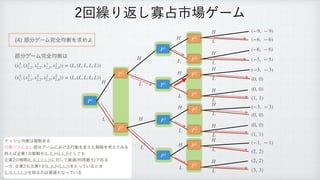
The document describes a reinforcement learning model. It defines a game with players N that take actions Si to maximize rewards fi over time. It introduces a discount factor δ and defines the discounted cumulative reward for a sequence of actions. The goal is to find the action sequence x* that maximizes this reward for each player, given other players' actions. Examples are provided to illustrate the model.

1. ήʔϜཧ࿦#4*$ԋश
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ

2. ੒෼ήʔϜ‫܁‬Γฦ͠ήʔϜʹ͓͚Δઓུ
‫܁‬Γฦ͠ήʔϜʹ͓͚Δརಘ‫ߧۉ‬
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
ఆཧ

3. ੒෼ήʔϜ
ϓϨΠϠʔͷू߹
ϓϨΠϠʔ ͷߦಈͷू߹
ϓϨΠϠʔ ͷརಘؔ਺ ͱͯ͠
‫܁‬Γฦ͠ήʔϜʹ͓͚Δઓུ
ͱͯ͠
ͱ͠
ͱ͢Δ
͜͜Ͱ
Λ ճ໨·Ͱͷཤྺͱ͍͏
ϓϨΠϠʔ ͷ ճ໨ͷߦಈ͸
ཤྺ Λ΋ͱʹܾఆ͞ΕΔ
͢ͳΘͪ Ͱ༩͑ΒΕΔ
͜ΕΑΓ‫܁‬Γฦ͠ήʔϜʹ͓͚ΔϓϨΠϠʔ ͷ७ਮઓུ͸ Ͱ༩͑ΒΕΔ
ϓϨΠϠʔ ͷ७ਮઓུͷू߹Λ ͱ͠
ϓϨΠϠʔશମͷઓུͷ૊ͷू߹Λ Ͱද͢
G = (N, {Si
}i∈N, {fi
}i∈N)
N
Si
i
fi
i S = S1
× ⋯ × Sn
fi
: S → ℜ
S = S1
× ⋯ × Sn
St−1 =
t−1
S × ⋯ × S S0 = {∅}
ht−1 = (s1, ⋯, st−1) ∈ St−1 t − 1
i t ht−1 xi
t : St−1 → Si
i xi
= (xi
t)T
t=1
i XTi
XT
= XT1
× ⋯ × XTn
੒෼ήʔϜ‫܁‬Γฦ͠ήʔϜʹ͓͚Δઓུ
‫܁‬Γฦ͞ΕΔήʔϜͷ͜ͱ

4. རಘ
ׂҾҼࢠ ͱͯ͠
ΛׂҾརಘͱ͍͏
‫܁‬Γฦ͠ήʔϜʹ͓͚Δφογϡ‫ߧۉ‬
ઓུ ͕φογϡ‫͋Ͱߧۉ‬Δͱ͸
͢΂ͯͷϓϨΠϠʔ ʹ͍ͭͯ
‫܁‬Γฦ͠ήʔϜʹ͓͚Δ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬
ઓུ ͕෦෼ήʔϜ‫׬‬શ‫͋Ͱߧۉ‬Δͱ͸
೚ҙͷ ͱ ճ໨·Ͱͷ೚ҙͷཤྺ ʹରͯ͠
ͱ ͔Βಋ͔ΕΔઓུͷ૊ ͕ ճ໨Ҏ߱ͷ෦෼ήʔϜͰφογϡ‫͋Ͱߧۉ‬Δ͜ͱΛ͍͏
δ, 0 δ 1
fTi
δ (x) =
T
∑
t=1
δt−1
fi
(st(x))
x* = (x1
* , ⋯, xn
*) i
fTi
δ (xi*
, x−i*
) ≥ fTi
δ (xi
, x−i*
), ∀xi
∈ XTi
x* = (x1
* , ⋯, xn
*) t = 1,2,⋯, T t − 1 ht−1
x* ht−1 x*
ht−1
t
‫܁‬Γฦ͠ήʔϜʹ͓͚Δརಘ‫ߧۉ‬

5. γϯϓϧͳՉ઎ࢢ৔ͷϞσϧΛߟ͑Δ
‫
ۀا‬͸ͦΕͧΕੜ࢈ྔ)JHI
·ͨ͸-PXΛఆΊ
ҎԼͷઓུ‫ܗ‬ήʔϜʢ੒෼ήʔϜʣΛϓϨΠ͢Δ
͜ͷͱ͖
ҎԼͷ໰͍ʹ౴͑Α
੒෼ήʔϜʹ͓͚Δ ७ઓུ
φογϡ‫ߧۉ‬Λ‫ٻ‬ΊΑ
͜ͷήʔϜΛճ‫܁‬Γฦ͢৔߹
֤‫ۀا‬ͷ७ઓུͷ‫਺ݸ‬Λ‫ٻ‬ΊΑ
ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ ల։‫ܗ‬ද‫Ͱݱ‬Α͍ʣ
෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-

6. γϯϓϧͳՉ઎ࢢ৔ͷϞσϧΛߟ͑Δ
‫
ۀا‬͸ͦΕͧΕੜ࢈ྔ)JHI
·ͨ͸-PXΛఆΊ
ҎԼͷઓུ‫ܗ‬ήʔϜʢ੒෼ήʔϜʣΛϓϨΠ͢Δ
͜ͷͱ͖
ҎԼͷ໰͍ʹ౴͑Α
੒෼ήʔϜʹ͓͚Δ ७ઓུ
φογϡ‫ߧۉ‬Λ‫ٻ‬ΊΑ
࠷ద൓ԠΛߟ͑Ε͹Α͍ -
-
͕φογϡ‫ߧۉ‬
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-

7. γϯϓϧͳՉ઎ࢢ৔ͷϞσϧΛߟ͑Δ
‫
ۀا‬͸ͦΕͧΕੜ࢈ྔ)JHI
·ͨ͸-PXΛఆΊ
ҎԼͷઓུ‫ܗ‬ήʔϜʢ੒෼ήʔϜʣΛϓϨΠ͢Δ
͜ͷͱ͖
ҎԼͷ໰͍ʹ౴͑Α
͜ͷήʔϜΛճ‫܁‬Γฦ͢৔߹
֤‫ۀا‬ͷ७ઓུͷ‫਺ݸ‬Λ‫ٻ‬ΊΑ
‫܁‬Γฦ͠ήʔϜʹ͓͚ΔઓུͷఆٛΑΓ
֤ཤྺʹରͯ͠ߦಈΛ༩͑Δؔ਺Λ·ͱΊͨ΋ͷ͕ઓུͰ͋Δ
‫͍ͯͭʹۀا‬ʢ‫͍ͯͭʹۀا‬΋ಉ༷
‫ظ‬໨ͰऔΒΕΔઓུͷ૊͸
)
)
)
-
-
)
-
-
ͷ̐௨Γ͋Γ
ͦΕͧΕʹ͍ͭͯ‫ظ‬໨ͷߦಈΛఆΊΔ͜ͱʹͳΔΏ͑ʹ Λ‫ۀا‬ͷ‫ظ‬໨ͷߦಈ
Λ‫ۀا‬ͷ‫ظ‬໨ͷߦಈ
ͨͩ͠
͸ )
)
ʹରͯ͠
͸ )
-
͸ -
)
͸ -
-
ʹରͯ͠ͷߦಈͱ͢Δͱ
ͱॻ͚ͯ
΋ ΋)·ͨ͸-ͳͷ͔ͩΒ
௨Γ͋Δ
x1
1 x1
2,k
k = 1 k = 2 k = 3 k = 4
(x1
1, (x1
2,1, x1
2,2, x1
2,3, x1
2,4)) x1
1 x1
2,k 25
= 32
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-

8. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L

9. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)

10. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)

11. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)
(−6 + 2δ, − 6 + 2δ)

12. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)
(−6 + 2δ, − 6 + 2δ)

13. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)
(−6 + 2δ, − 6 + 2δ)
(0 + (−6)δ, 0 + (−6)δ)

14. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)
(−6 + 2δ, − 6 + 2δ)
(0 + (−6)δ, 0 + (−6)δ)
(0 + 0δ, 0 + 0δ)

15. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−6 + (−6)δ, − 6 + (−6)δ)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
H
L
(−6 + 0δ, − 6 + 0δ)
(−6 + 0δ, − 6 + 0δ)
(−6 + 2δ, − 6 + 2δ)
(0 + (−6)δ, 0 + (−6)δ)
(0 + 0δ, 0 + 0δ)
(0 + 0δ, 0 + 0δ)
(0 + 2δ, 0 + 2δ)
(0 + (−6)δ, 0 + (−6)δ)
(0 + 0δ, 0 + 0δ)
(0 + 0δ, 0 + 0δ)
(0 + 2δ, 0 + 2δ)
(2 + (−6)δ, 2 + (−6)δ)
(2 + 0δ, 2 + 0δ)
(2 + 0δ, 2 + 0δ)
(2 + 2δ, 2 + 2δ)

16. ׂҾҼࢠ ͱ͠
֤‫ۀا‬ͷׂҾརಘΛ‫ٻ‬ΊΑ
δ = 0.5
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)

17. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)

18. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
̍ʘ ) -
)
-

19. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
̍ʘ ) -
)
-

20. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
̍ʘ ) -
)
-

21. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
̍ʘ ) -
)
-

22. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)

23. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
৘ใू߹
‫ۀا‬
P1
‫ۀا‬
P2
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
̍ʘ ) -
)
-
ॖ໿ήʔϜʹ͓͚Δརಘද
(−5, − 5)
(1, 1)
(1, 1)
(3, 3)

24. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
෦෼ήʔϜ‫׬‬શ‫ߧۉ‬͸
(x1
1, (x1
2,1, x1
2,2, x1
2,3, x1
2,4)) = (L, (L, L, L, L))
(x2
1, (x2
2,1, x2
2,2, x2
2,3, x2
2,4)) = (L, (L, L, L, L))
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)

25. ఆཧ
੒෼ήʔϜ͕ͨͩҰͭͷφογϡ‫ߧۉ‬ Λ΋ͭͱ͢Δ͜ͷͱ͖ ճ‫܁‬Γฦ͠ήʔϜʹ͓͚Δ
෦෼ήʔϜ‫׬‬શ‫ߧۉ‬ ͸ͨͩҰͭଘࡏ͠
ߦಈͷ૊ Λ༩͑Δ
ࠓճԋशͰ༻͍ͨήʔϜ΋੒෼ήʔϜͰͨͩҰͭͷφογϡ‫ ߧۉ‬-
-
Λ͍࣋ͬͯͨͷͰ
ఆཧΑΓ֤‫
ظ‬ཤྺʹؔΘΒͣ -
-
Λ༻͍ΔΑ͏ͳઓུͷ૊͕෦෼ήʔϜ‫׬‬શ‫ͳͱߧۉ‬Δ
s* T
x* s(x*) = (
T
s*, s*, ⋯, s*)
ఆཧ
̍ʘ ) -
)
-

26. ෦෼ήʔϜ‫׬‬શ‫ߧۉ‬Λ‫ٻ‬ΊΑ
෦෼ήʔϜ‫׬‬શ‫ߧۉ‬͸
(x1
1, (x1
2,1, x1
2,2, x1
2,3, x1
2,4)) = (L, (L, L, L, L))
(x2
1, (x2
2,1, x2
2,2, x2
2,3, x2
2,4)) = (L, (L, L, L, L))
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
̍ʘ ) -
)
-
P1
(−9, − 9)
H
P2
P2
P1
P2
P2
P1
P2
P2
P1
P2
P2
P2
P2
P1
(−6, − 6)
H
H
H
L
L
L
H
L
L
H
L
H
L
H
L
(−6, − 6)
(−5, − 5)
H
L
(−3, − 3)
(0, 0)
H
L
(1, 1)
H
L
(−3, − 3)
(0, 0)
H
L
(0, 0)
(1, 1)
H
L
(−1, − 1)
(2, 2)
H
L
(2, 2)
(3, 3)
H
L
(0, 0)
φογϡ‫ߧۉ‬͸ෳ਺͋Δ
‫ߧۉ‬ύεʹͳ͍෦෼ήʔϜʹ͓͚ΔߦಈΛม͑ͨઓུΛߟ͑ͯΈΔ
ྫ͑͹‫ۀا‬ͷઓུΛ -
-
)
-
-
ͱͯ͠΋
‫ۀا‬ͷઓུ -
-
-
-
-
ʹରͯ͠࠷ద རಘ࠷େ
Ͱ͋Δ
Ұํ
‫ۀا‬΋‫ ͕ۀا‬-
-
)
-
-
Λͱ͍ͬͯΔͱ͖
-
-
-
-
-
ΛऔΔͷ͸࠷దͱͳ͍ͬͯΔ

27. ఆཧ
੒෼ήʔϜ͕ͨͩҰͭͷφογϡ‫ߧۉ‬ Λ΋ͪ
͢΂ͯͷϓϨΠϠʔ ͷ‫ߧۉ‬རಘ͕
ϛχϚοΫεརಘ ʹ౳͍͠ͱ͢Δ͜ͷͱ͖
೚ҙͷ ʹରͯ͠
ճ‫܁‬Γฦ͠ήʔϜʹ͓͚Δφογϡ‫఺ߧۉ‬͸ ͸ͨͩҰͭଘࡏ͠
ߦಈͷ૊ Λ༩͑Δ
ϛχϚοΫεߦಈͱϛχϚοΫεརಘ
੒෼ήʔϜ ʹ͓͍ͯ
Λຬͨ͢ϓϨΠϠʔ Ҏ֎ͷߦಈͷ૊ Λ ʹର͢ΔϛχϚοΫεߦಈͱ͍͏
͜ͷ ΛϛχϚοΫεརಘΛ͍͍
Ͱද͢ ΛϛχϚοΫε఺ͱ͍͏
s* i ∈ N
vi
T = 1,2,⋯
T x* s(x*) = (
T
s*, s*, ⋯, s*)
G
max
si
fi
(si
, ̂
s−i
) = min
s−i
max
si
fi
(si
, s−i
)
i ̂
s−i
i
max
si
fi
(si
, ̂
s−i
) vi
v = (v1
, ⋯, vn
)
ఆཧ
̍ʘ ) -
)
-
৚͕݅૿͑ͯΔ
ࠓճͷ੒෼ήʔϜʹ͓͚ΔϛχϚοΫεརಘ͸‫ۀا‬΋‫ۀا‬΋
φογϡ‫͚͓ʹߧۉ‬Δརಘʹ౳͘͠ͳ͍
ӈͷΑ͏ͳनਓͷδϨϯϚͩͱ
φογϡ‫ߧۉ‬ͷརಘͱϛχϚοΫεརಘ͕Ұக͢ΔͷͰ
༗‫ݶ‬ճ‫܁‬Γฦ͠ήʔϜʹ͓͚Δφογϡ‫Ͱߧۉ‬͸ %
%
͕औΒΕଓ͚Δ
̍ʘ $ %
$
%

28. ήʔϜཧ࿦#4*$ԋश
ճ‫܁‬Γฦ͠Չ઎ࢢ৔ήʔϜ
࣍ճɿԋश