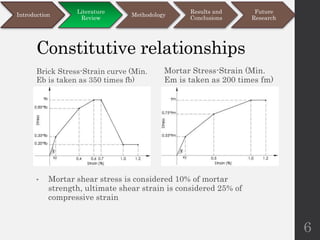
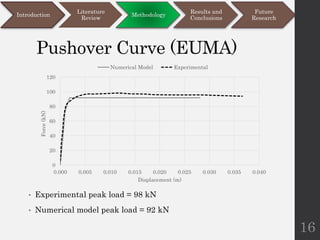
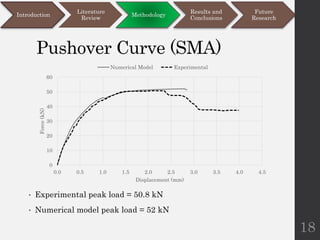
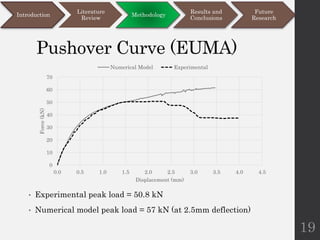
This document discusses different modeling approaches for finite element analysis of masonry structures. It compares the springs modeling approach and expanded units modeling approach by applying them to numerically model and analyze the behavior of four experimental masonry walls under various static and pseudo-dynamic loading conditions. Both approaches are able to predict the load capacities of the walls with reasonable accuracy compared to experimental data, but the expanded units approach is found to be more versatile and accurate. The document also outlines future research directions around improving the accuracy and capabilities of the modeling approaches.

1. Introduction
• Researches these days are most focused on
Finite element modeling
• Prime objective of finite element modeling is
to achieve results without having to spend
time and money on laboratory experiments
1
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

2. Introduction
• Masonry is the most commonly used
construction material in Pakistan and world
over (Rafiq, 2015)
• Seismic forces induce in-plane loads in shear
walls
• Understanding of masonry behavior under in-
plane static and cyclic loading is of prime
importance
2
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

3. Literature Review
• There are three major finite element modeling
techniques for masonry (Lourenco and Rots,
1994)
1. Detailed micro-modeling
2. Simplified micro-modeling
3. Macro modeling
3
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

4. Simplified micro-modeling
• Two methods have been used in the literature
under simplified micro modeling
1. Springs modeling approach (Campbell,
2012), (Drougkas, 2014).
2. Expanded Units modeling approach
(Abdulla, 2017), (Lourenco, 1996).
4
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

5. Springs modeling approach
• This approach considers brick units connected with
mortar through contact elements (interface).
Mortar is defined using non-linear springs.
• Brick & mortar material constitutive relationships
are defined as per pre-defined criteria
• Contact normal and tangential stiffness are
defined by:
𝐾𝑛 =
𝐸𝑚. 𝐴𝑡𝑟𝑖𝑏
𝐿
𝐾𝑠 =
𝐺𝑚. 𝐴𝑡𝑟𝑖𝑏
𝐿
5
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

6. Constitutive relationships
Brick Stress-Strain curve (Min.
Eb is taken as 350 times fb)
Mortar Stress-Strain (Min.
Em is taken as 200 times fm)
6
• Mortar shear stress is considered 10% of mortar
strength, ultimate shear strain is considered 25% of
compressive strain
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

7. Expanded units modeling
approach
• This approach considers the brick unit as an
‘expanded unit’
• The dimensions of brick are expanded to half
mortar thickness on each side
• The brick properties are adjusted to account
for this approximation
𝐸𝑎𝑑𝑗 =
𝐻𝐸𝑏𝐸𝑚
𝑛ℎ𝑏𝐸𝑚 + (𝑛 − 1)ℎ𝑚𝐸𝑏
7
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

8. Material properties
• Drucker Prager’s (DP) non-linear
properties are defined for expanded units.
• DP input requires cohesion (c) and friction
angle (ϕ)
• Contact normal and tangential stiffness
defined by:
𝑘𝑛 =
𝐸𝑏𝐸𝑚
ℎ𝑚 𝐺𝑏 − 𝐺𝑚
; 𝑘𝑠 =
𝐺𝑏𝐺𝑚
ℎ𝑚 𝐺𝑏 − 𝐺𝑚
8
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

9. Cohesive zone material
• Cohesive zone material (CZM) law is defined
to model contact delamination with increasing
stresses (ANSYS, 2015).
• Maximum applied stresses and critical
fracture energy values are defined under the
CZM law
9
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

10. Problem Statement
• Compilation of various modeling approaches
is desired; different methodologies have not
been tested on similar problems for apple-to-
apple comparison
• Springs modeling approach is computationally
economical but needs improved accuracy
• Expanded units modeling approach provides
more accurate results but computationally
very expensive; efficiency can be improved
• This complex approach also needs
simplification by problem size reduction to
cater for limitations of ‘Student releases’
10
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

11. Research Objectives
• To define the numerical model based on the
most efficient approach to reproduce the
mechanical behavior of the masonry walls.
• To evaluate the results of the numerical model
in comparison with the already available
experimental data, and
• To predict the capacity of the tested walls.
11
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

12. Methodology
12
• 4 different walls have been modeled in ANSYS
• Springs modeling approach (SMA) and
Expanded units modeling approach (EUMA)
are applied on each of these walls
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
Wall
Loading
type
Wall dimensions
Vertical
Pressure
Wall A
In-plane
static
1250x2500x175 mm 1.00 MPa
Wall B 990x1000x100 mm 0.30 MPa
Wall C 990x1000x100 mm 1.21 MPa
Wall D
In-plane
pseudo-
dynamic
1200x1200x110 mm 0.70 MPa

13. Mesh Sensitivity study
• Springs modeling approach is found to be
unaffected by mesh size, therefore, minimum
possible mesh sizes are used
• Expanded units modeling approach tested for:
 7x3x2 elements per brick (Fig. a)
 3x1x1 elements per brick (Fig. b)
• Coarser mesh (Fig. b) is six times quicker with
no bearing on accuracy of results. Hence, this
mesh size is adopted
13
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

14. Wall A
In-plane Static loading
14
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

15. Pushover Curve (SMA)
• Experimental peak load = 98 kN
• Numerical model peak load = 103 kN
15
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
0
20
40
60
80
100
120
0.000 0.005 0.010 0.015 0.020 0.025 0.030 0.035 0.040
Force
(kN)
Displacement (m)
Numerical Model Experimental

16. Pushover Curve (EUMA)
• Experimental peak load = 98 kN
• Numerical model peak load = 92 kN
16
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
0
20
40
60
80
100
120
0.000 0.005 0.010 0.015 0.020 0.025 0.030 0.035 0.040
Force
(kN)
Displacement (m)
Numerical Model Experimental

17. Wall B
In-plane Static loading
17
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

18. Pushover Curve (SMA)
• Experimental peak load = 50.8 kN
• Numerical model peak load = 52 kN
18
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
0
10
20
30
40
50
60
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
Force
(kN)
Displacement (mm)
Numerical Model Experimental

19. Pushover Curve (EUMA)
• Experimental peak load = 50.8 kN
• Numerical model peak load = 57 kN (at 2.5mm deflection)
19
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
0
10
20
30
40
50
60
70
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
Force
(kN)
Displacement (mm)
Numerical Model Experimental

20. Wall C
In-plane Static loading
20
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

21. Pushover Curve (EUMA)
• Experimental peak load = 72 kN
• Numerical model peak load = 76 kN (at 2.0mm deflection)
21
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
0
10
20
30
40
50
60
70
80
90
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Force
(kN)
Displacement (mm)
Numerical Model Experimental

22. Wall D
In-plane pseudo-dynamic loading
22
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research

23. Results and Conclusions
23
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
• While Springs modeling approach (SMA) is
quicker, Expanded units modeling approach
(EUMA) is more versatile and accurate in
most loading conditions
• EUMA is analyzed in a much computationally
efficient way by reduction of problem size
without compromise on accuracy
• All models have predicted the capacity of
walls with reasonable accuracy, in comparison
to the experimental data.
• SMA, however, has not been able to predict
the cyclic behavior of the walls

24. Future Research
24
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
• Development of an SMA model which can
accurately predict the cyclic behavior by
introducing more stability into the model
• Development of flexibility in SMA for varying
wall stiffnesses
• Use of latest versions of ANSYS software for
EUMA & ‘Workbench’ module which considers
cracking within the solid elements without the
need for remeshing
• Introduction of post-peak softening in EUMA
with more accuracy

25. References
25
Introduction
Literature
Review
Methodology
Results and
Conclusions
Future
Research
• Abdulla, K. F., Cunningham, L. S., & Gillie, M. (2017). Simulating masonry
wall behaviour using a simplified micro-model approach. Engineering
Structures, 151, 349-365. doi:10.1016/j.engstruct.2017.08.021
• ANSYS. (2015). ANSYS Analysis Reference Manual. ANSYS.
• Campbell, J. B. (2012). Numerical Model for Nonlinear Analysis of Masonry
Walls. University of La Serena
• Drougkas, A., Pela, L., & Roca, P. (2014). Numerical Modelling of Masonry
Shear Walls Failure Mechanisms. 9th International Masonry Conference.
Guimarães: International Masonry Society.
• Lourenço, P. B. (1996). Computational Strategies for Masonry Structures.
• Lourenço, P. B., & Rots, J. G. (1994). Analysis of Masonry Structures with
Interface elements; Theory and Applications.
• Mojsilovic´, N., Simundic, G., & Page, A. (2010). Masonry wallettes with
damp-proof course membrane subjected to cyclic shear: An experimental
study. Construction and Building Materials, 24, 2135-2144.
• Rafiq, A. (2015). Computational Modeling of an Unconfined/ Unreinforced
Masonry wall using ABAQUS.

26. Thank You
26