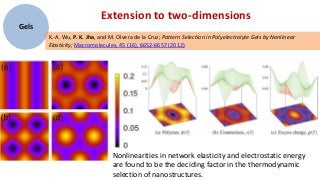
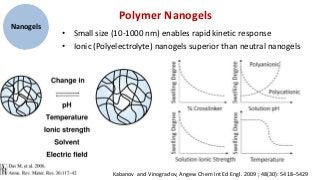
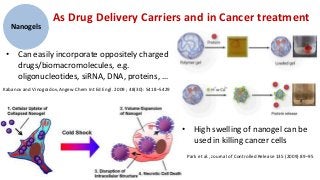
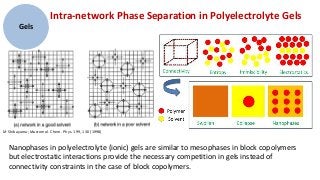
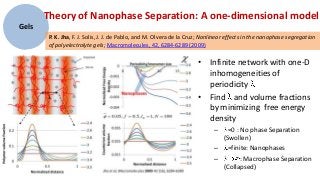
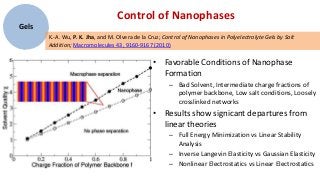
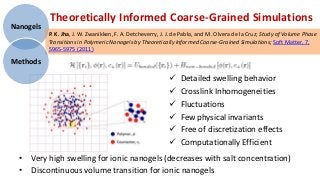
1) The document discusses research on polymer gels, nanogels, and their applications in drug delivery. 2) Simulation methods and theoretical models are used to study the phase behavior, swelling properties, and self-assembly of polyelectrolyte gels and nanogels under different conditions. 3) Ongoing work includes atomistic simulations of polymer-drug interactions to inform drug delivery applications of gels and nanogels.

1. Research Focus
Gels Drug
Molecular Simulations Delivery
Thermodynamics
Polymer Physics
Nanoscience Polymers
Nanogels
Self-
Methods
Assembly

2. Polymer Gels
Gels
• Solvent-permeated networks of polymer chains
• Highly responsive: Large volume changes by gaining/
losing solvent with changes in T, pH, external field
• Applications: Superabsorbers, Cosmetics, Contact lenses,
Drug Delivery, Tissue Engineering, Artificial Muscles,
Microfluidics,
F Horkay and G McKenna; Physical Properties of Polymers Handbook; 2007, Part V, 497-523

3. Intra-network Phase Separation in Polyelectrolyte Gels
Gels
M Shibayama; Macromol. Chem. Phys. 199, 130 (1998)
Nanophases in polyelectrolyte (ionic) gels are similar to mesophases in block copolymers
but electrostatic interactions provide the necessary competition in gels instead of
connectivity constraints in the case of block copolymers.

4. Theory of Nanophase Separation: A one-dimensional model
Gels
P. K. Jha, F. J. Solis, J. J. de Pablo, and M. Olvera de la Cruz; Nonlinear effects in the nanophase segregation
of polyelectrolyte gels; Macromolecules, 42, 6284-6289 (2009)
• Infinite network with one-D
inhomogeneities of
periodicity
• Find and volume fractions
by minimizing free energy
density
– =0 : No phase Separation
(Swollen)
– =finite: Nanophases
– : Macrophase Separation
(Collapsed)

5. Control of Nanophases
Gels
K.-A. Wu, P. K. Jha, and M. Olvera de la Cruz; Control of Nanophases in Polyelectrolyte Gels by Salt
Addition; Macromolecules 43, 9160-9167 (2010)
• Favorable Conditions of Nanophase
Formation
– Bad Solvent, Intermediate charge fractions of
polymer backbone, Low salt conditions, Loosely
crosslinked networks
• Results show signicant departures from
linear theories
– Full Energy Minimization vs Linear Stability
Analysis
– Inverse Langevin Elasticity vs Gaussian Elasticity
– Nonlinear Electrostatics vs Linear Electrostatics

6. Extension to two-dimensions
Gels
K.-A. Wu, P. K. Jha, and M. Olvera de la Cruz; Pattern Selection in Polyelectrolyte Gels by Nonlinear
Elasticity; Macromolecules, 45 (16), 6652-6657 (2012)
Nonlinearities in network elasticity and electrostatic energy
are found to be the deciding factor in the thermodynamic
selection of nanostructures.

7. Polymer Nanogels
Nanogels
• Small size (10-1000 nm) enables rapid kinetic response
• Ionic (Polyelectrolyte) nanogels superior than neutral nanogels
Kabanov and Vinogradov, Angew Chem Int Ed Engl. 2009 ; 48(30): 5418–5429

8. As Drug Delivery Carriers and in Cancer treatment
Nanogels
• Can easily incorporate oppositely charged
drugs/biomacromolecules, e.g.
oligonucleotides, siRNA, DNA, proteins, …
Kabanov and Vinogradov, Angew Chem Int Ed Engl. 2009 ; 48(30): 5418–5429
• High swelling of nanogel can be
used in killing cancer cells
Park et al., Journal of Controlled Release 135 (2009) 89–95

9. Poisson-Boltzmann Theory
Nanogels
P. K. Jha, J. W. Zwanikken, J. J. de Pablo, and M. Olvera de la Cruz; Electrostatic Control of Nanoscale Phase
Behavior of Polyelectrolyte Networks; Current Opinion in Solid State and Materials Science, 15(6), 271-276
(2011)
• Mobile ion concentrations by mean-field
approximation
• Smaller, collapsed, and gels at low salt
concentration or in high dielectric solvent
have larger excess charge
Donnan theory fails

10. Modified Donnan Theory
Nanogels
P. K. Jha, J. W. Zwanikken, and M. Olvera de la Cruz; Understanding Swollen-Collapsed and Re-entrant
Transitions in Polyelectrolyte Nanogels by a Modified Donnan Theory; Soft Matter (Communication), 8,
9519-9522 (2012)
• For nanogels at high salt
concentrations, inclusion of the
excluded volume effect of ions
predicts a re-entrant behavior
similar to that found in mitotic
chromosomes
• Effects of a neutral component,
salt valence, and dielectric
mismatch, on the optimal
compaction of nanogels are
analyzed

11. Theoretically Informed Coarse-Grained Simulations
Nanogels
P. K. Jha, J. W. Zwanikken, F. A. Detcheverry, J. J. de Pablo, and M. Olvera de la Cruz; Study of Volume Phase
Transitions in Polymeric Nanogels by Theoretically Informed Coarse-Grained Simulations; Soft Matter, 7,
5965-5975 (2011)
Methods
 Detailed swelling behavior
 Crosslink Inhomogeneities
 Fluctuations
 Few physical invariants
 Free of discretization effects
 Computationally Efficient
• Very high swelling for ionic nanogels (decreases with salt concentration)
• Discontinuous volume transition for ionic nanogels

12. Charges on the GPU
Methods
P. K. Jha, R. Sknepnek, G. I. Guerrero-Garcia, M. Olvera de la Cruz; A Graphics Processing Unit
Implementation of Coulomb Interaction in Molecular Dynamics; Journal of Chemical Theory and
Computation, 6, 3058 (2010)
GPU implementation of long-range electrostatic
interactions based on the orientation-averaged
Ewald sum (ES) scheme introduced by Yakub and
Ronchi (YR).
Yakub and Ronchi,JCP, 2003, 119, 11556

13. Charges on the GPU
Methods
P. K. Jha, R. Sknepnek, G. I. Guerrero-Garcia, M. Olvera de la Cruz; A Graphics Processing Unit
Implementation of Coulomb Interaction in Molecular Dynamics; Journal of Chemical Theory and
Computation, 6, 3058 (2010)
GPU implementation of long-range electrostatic
interactions based on the orientation-averaged
Ewald sum (ES) scheme introduced by Yakub and
Ronchi (YR).
Yakub and Ronchi,JCP, 2003, 119, 11556

14. Kinetic Monte Carlo Simulations
Methods
P. K. Jha, V. Kuzovkov, B. A. Grzybowski, and M. Olvera de la Cruz; Dynamic Self-Assembly of Photo-
switchable nanoparticles; Soft Matter, 8, 227-234 (2012)
P. K. Jha, V. Kuzovkov, and M. Olvera de la Cruz; Kinetic Monte Carlo Simulations of Flow-Assisted
Polymerization; ACS Macro Letters, 2012, 1, pp 1393--1397 (2012)
•
Off-lattice with fixed step size :
Randomly pick spherical
coordinates , in 3D
• Time-step independent of
magnitude of forces (determined
by the step size)
• Unphysical moves have transition
probability=0 (NOT allowed)
Transition probability in kinetic Monte Carlo scheme
= Transition rate in a renormalized master equation of diffusion

15. Light-induced Self Assembly
Self-
Assembly P. K. Jha, V. Kuzovkov, B. A. Grzybowski, and M. Olvera de la Cruz; Dynamic Self-Assembly of Photo-
switchable nanoparticles; Soft Matter, 8, 227-234 (2012)
Methods
• Simple model with features representative of
experiments by Klajn et al, PNAS, 104 (25),
10305-10309 (2007)
• Experimental time scales of aggregation and
disassembly agree with simulations
• Energetics vs Kinetics: ”flexible”, ”frozen”,
”fluctuating” and percolated ”network-like”
structures

16. Flow-assisted Polymerization
Methods
P. K. Jha, V. Kuzovkov, and M. Olvera de la Cruz; Kinetic Monte Carlo Simulations of Flow-Assisted
Polymerization; ACS Macro Letters, 2012, 1, pp 1393--1397 (2012)
Polymers
• Model of a polymerization process in the
presence of a periodic oscillatory flow to explore
the role of mixing in polymerization reactors
• Flow field helps overcome the diffusive
limitations that develop during a polymerization
process high rates of polymerization
• “dynamic” coil–stretch transition with increase in
flow-strength

17. Work in Progress
Polymers
Atomistic Simulations of Polymer-Drug Interactions
Drug
Delivery

18. • Professor Monica Olvera de la Cruz
Acknowledgments Northwestern University
• Professor Ronald G. Larson
University of Michigan-Ann Arbor
Self- Drug
Gels Nanogels Methods Assembly Polymers Delivery