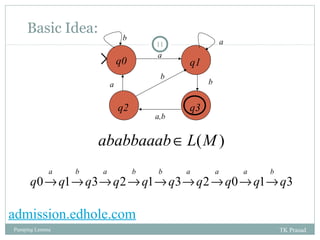
This document discusses regular languages and the pumping lemma for regular languages. It begins by defining regular languages and their representations using finite automata, regular expressions, and regular grammars. It then introduces the pumping lemma, which states that for any regular language, there exists a length such that any string in the language of that length or greater can be decomposed and pumped to generate new strings that are also in the language. The document provides examples of using the pumping lemma to prove languages are non-regular by finding a string that cannot be pumped in the required way. It concludes by summarizing different proof techniques used with the pumping lemma.

1. MBA Admission in India
BY:
ADMISSION.EDHOLE.COM

2. 2
Nonregularity Proofs
admission.edhole.com
Pumping Lemma TK Prasad

3. Regular Languages: GGrraanndd UUnniiffiiccaattiioonn
3
L NFA -l s =
L NFAs
( ) ( )
L DFAs
( )
=
L(FA) = L(RE)
L(FA) = L(RG) (Construction)
L(RG) = L(RE)
(Parallel Simulation)
(Rabin and Scott’s work)
(Collapsing graphs;
Structural Induction)
(S. Kleene’s work)
(Solving linear
equations)
admission.edhole.com
Pumping Lemma TK Prasad

4. Role of various representations
for Regular Languages
4
Closure under complemention. (DFAs)
Closure under union, concatenation, and
Kleene star. (NFA-ls, Regular expression.)
 Consequence:
Closure under intersection by De Morgan’s Laws.
Relationship to context-free languages.
(Regular Grammars.)
Ease of specification. (Regular expression.)
Building tokenizers/lexical analyzers. (DFAs)
admission.edhole.com
Pumping Lemma TK Prasad

5. Show L = {aibi | i ³ 0} is not regular.
5
Consider pairs of strings:
n
u a aa a
' : ... ...
n
i s
v b bb b
' : ... ...
i s
If L were regular, then there exists a DFA MM
accepting L with the following property:
i i
q a b F
( , )
i j
Î
0
q a b F i j
d
*
M
d
M
Ï ¹
( , ) if
0
*
*
d * d
q a b q aib j i j
( , ) ¹ ( , ) if ¹ M M
0
i i
0
admission.edhole.com
Pumping Lemma TK Prasad

6. *
CLAIM:
d * d
q a q a j i j
( , ) ¹ ( , ) if ¹ M M
0
i
0
JUSTIFICATION: Otherwise, from the definition of DFA,
*
d * d
q a b q a jbi i j
( , ) = ( , ) for ¹ M M
0
i i
0
which contradicts the earlier conclusion.
In order to satisfy
*
d * d
q a q a j i j
( , ) ¹ ( , ) if ¹ M M
0
i
0
the machine M must have a unique state for every i.
Thus, M must have iinnffiinniittee number of states, if L
is regular. This violates the definition of DFA.
So, L must be non-regular. admission.edhole.com
Pumping Lemma 6 TK Prasad

7. Using Closure Properties
 Regular languages are closed under set-intersection. 7
L = L Ç
L
 Note that regularity is a property of a collection, and not a property of an individual string in the collection.
1 2
L L
= Ç
1 2
L L
= È
1 2
L1=bit strings with even parity
L2=bit strings with number of 1’s divisible by 3
L=bit strings with number of 1’s a multiple of 6
admission.edhole.com
Pumping Lemma TK Prasad

8. If R is a regular language and C is context-free,
RÇC
then may not be regular.
8
Proof:
R a b
=
* *
{ i i
| 0}
C a b i
= ³
R Ç C =
C
• Show that
is not regular.
• Proof: If L were regular, ought to be
regular. However, is known to be
non-regular. Hence, L cannot be regular.
L = {w Î{a,b}* | # a' s in w = #b's in w}
LÇ R
LÇ R = C
admission.edhole.com
Pumping Lemma TK Prasad

9. Prelude to Pumping Lemma
9
Is 46551 divisible by 46?
Is 46554 divisible by 46?
Is 46552 divisible by 46?
Necessary vs sufficient condition
admission.edhole.com
Pumping Lemma TK Prasad

10. Pumping Lemma for Regular Languages
10
It is a necessary condition.
 Every regular language satisfies it.
 If a language violates it, it is not regular.
 RL => PL not PL => not RL
It is not a sufficient condition.
 Not every non-regular language violates it.
 not RL =>? PL or not PL (no conclusion)
admission.edhole.com
Pumping Lemma TK Prasad

11. Basic Idea:
b a
11
q0
a
a
b
q1
q2 q3
a,b
b
ababbaaabÎL(M)
a b a b b a a a b
® ® ® ® ® ® ® ® ®
q0 q1 q3 q2 q1 q3 q2 q0 q1 q3
admission.edhole.com
Pumping Lemma TK Prasad

12. Note,
a b a b b a a a b
® ® ® ® ® ® ® ® ®
q0 q1 q3 q2 q1 q3 q2 q0 q1 q3
So, ababbÎL(M)
a b a b b a a a b
® ® ® ® ® ® ® ® ®
q0 q1 q3 q2 q1 q3 q2 q0 q1 q3
abaaabÎL(M)
"i, jÎN : ab(abb)i (aaab) j ÎL(M)
admission.edhole.com
Pumping Lemma 12 TK Prasad

13. Fundamental 13
Observation
Given a “sufficiently” long string, the states of a
DFA must repeat in an accepting computation.
These cycles can then be used to predict
(generate) infinitely many other strings in (of)
the language.
Pigeon-Hole Principle
admission.edhole.com
Pumping Lemma TK Prasad

14. Pumping Lemma
Let L be a regular langu14age that is accepted by a
DFA M with k states. Let z be any string in L
with . Then length(z can z) ³ be k
decomposed
as uvw with
length uv k
( ) ,
length v
£
>
( ) 0, and
" ³ i Î
i 0 :
uv w L
admission.edhole.com
Pumping Lemma TK Prasad

15. For all sufficiently long strings (z)
There exists non-null prefix (uv)
15
and substring (v)
For all repetitions of the substring
(v),
we get strings in the language.
s L s k
" Î ³ Þ
: | |
u,v,w uvw s
$ =
: ( )
uv k v
Ù £ Ù >
( | | ) ( | | 0)
Ù " ³ Þ i Î
i i uv w L
( : 0 )
admission.edhole.com
Pumping Lemma TK Prasad

16. Proving non-regularity
16
Î
If there exists an arbitrarily long string s L,
and for each decomposition s = uvw, there
exists an i such that , then L is non-regular.
uviwÏL
Negation of the necessary condition:
s L s k
$ Î ³ Ù
: | |
u,v,w uvw s
" =
: ( )
uv k v
Ù £ Ù >
( | | ) ( | | 0)
Þ $ ³ Ù i Ï
i i uv w L
( : 0 )
admission.edhole.com
Pumping Lemma TK Prasad

17. 17 Examples
APPLYING PUMPING LEMMA
admission.edhole.com
Pumping Lemma TK Prasad

18. L {a p | p is a prime number}
p =
is not regular.
18
Proof by contradiction:
Let L
be accepted by a k-state DFA.
p Choose
For all prefixes of length
show there exists such that
i.e.,
s = an , where n is a prime ³ k
j £ k,
i , (a j )i j an- j ÏL
j p
( j i n j) is a composite number. j * + -
admission.edhole.com
Pumping Lemma TK Prasad

19. i = n +1 j
(For this specific problem happens to be independent of
j, but that need not always 19
be the case.)
Choose
j i
j* n + + n - j = n*j +
n
n j
= +
*( 1)
composite number!
( 1)
 is non-regular because it violates the
necessary condition.
p L
an+ an- ÏL a n + a n
- ÏL
1 1 , ( 2 ) 1 2 ,...
p
p
admission.edhole.com
Pumping Lemma TK Prasad

20. L {anbm | n m}
p = >
20
Proof : (For this example, choice of initial string is
crucial.)
s = an where n > number of states of DFA
For this choice of s, the pumping lemma cannot
generate a contradiction!
However, let s = an+1bn
instead.
Original String :
Pumped String :
j n j n
= + -
s a a b
i * j n + 1
-
j n
1
a a b
admission.edhole.com
Pumping Lemma TK Prasad

21. 21 For
i = Ù n ³ j
³
Þ + - £
0 1
n 1
j n
Thus, by pumping the substring containing a’s
0 times (effectively deleting it), the number of
a’s can be made smaller than the number of b’s.
So, by pumping lemma, L is non-regular.
admission.edhole.com
Pumping Lemma TK Prasad

22. L {ac | c is a composite number}
c =
is not regular.
22
Proof by contradiction:
c a* - L
c L . c L
 If is regular, then so is , the complement
of
a* - L = L
c p  But which is known to be non-regular.
c L
 So, cannot be regular.
admission.edhole.com
Pumping Lemma TK Prasad

23. Summary: Proof Techniques
23
Counter Examples
Constructions/Simulations
 Induction Proofs
Impossibility Proofs
 Proofs by Contradiction
Reduction Proofs : Closure Properties
admission.edhole.com
Pumping Lemma TK Prasad