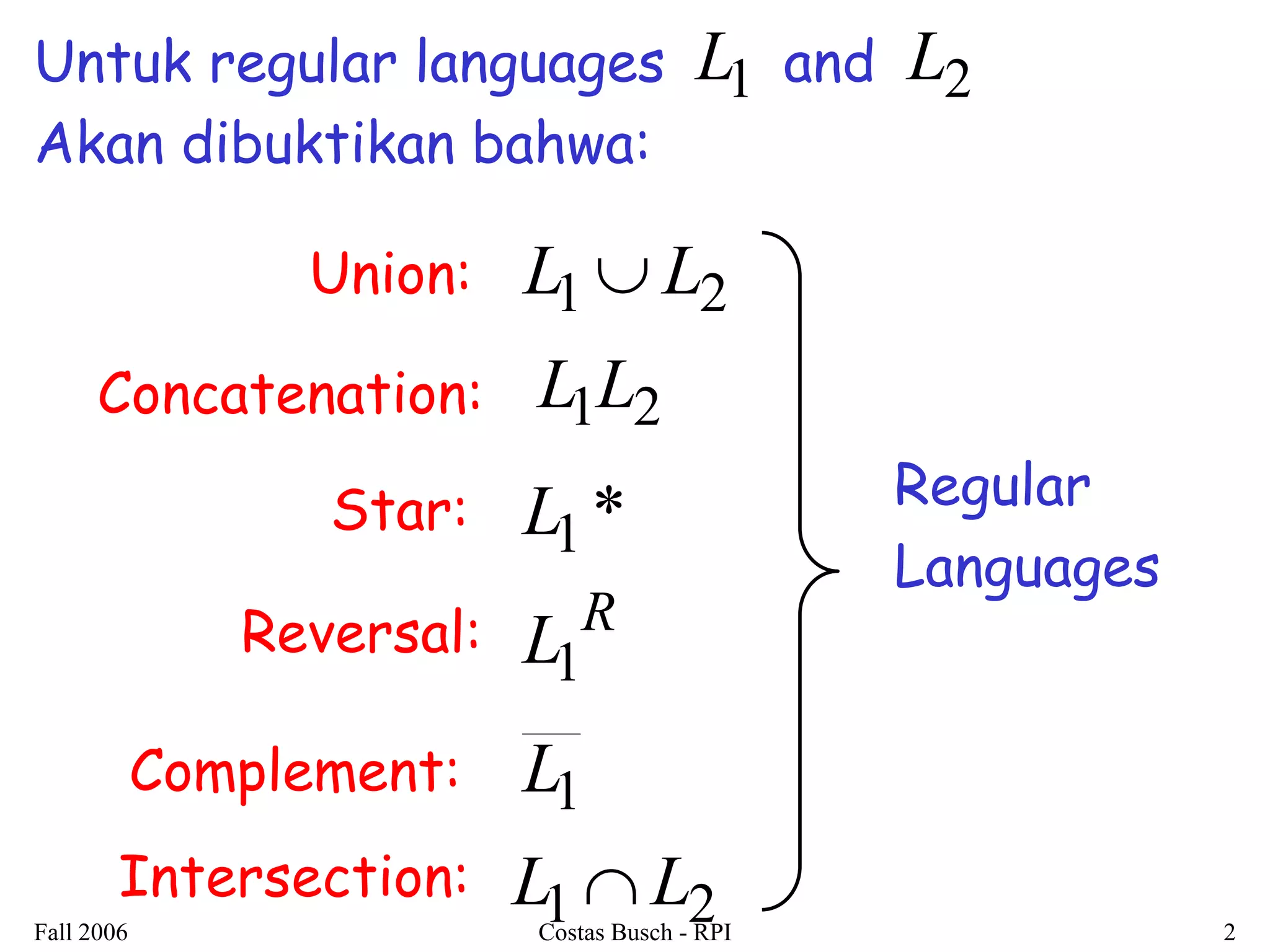
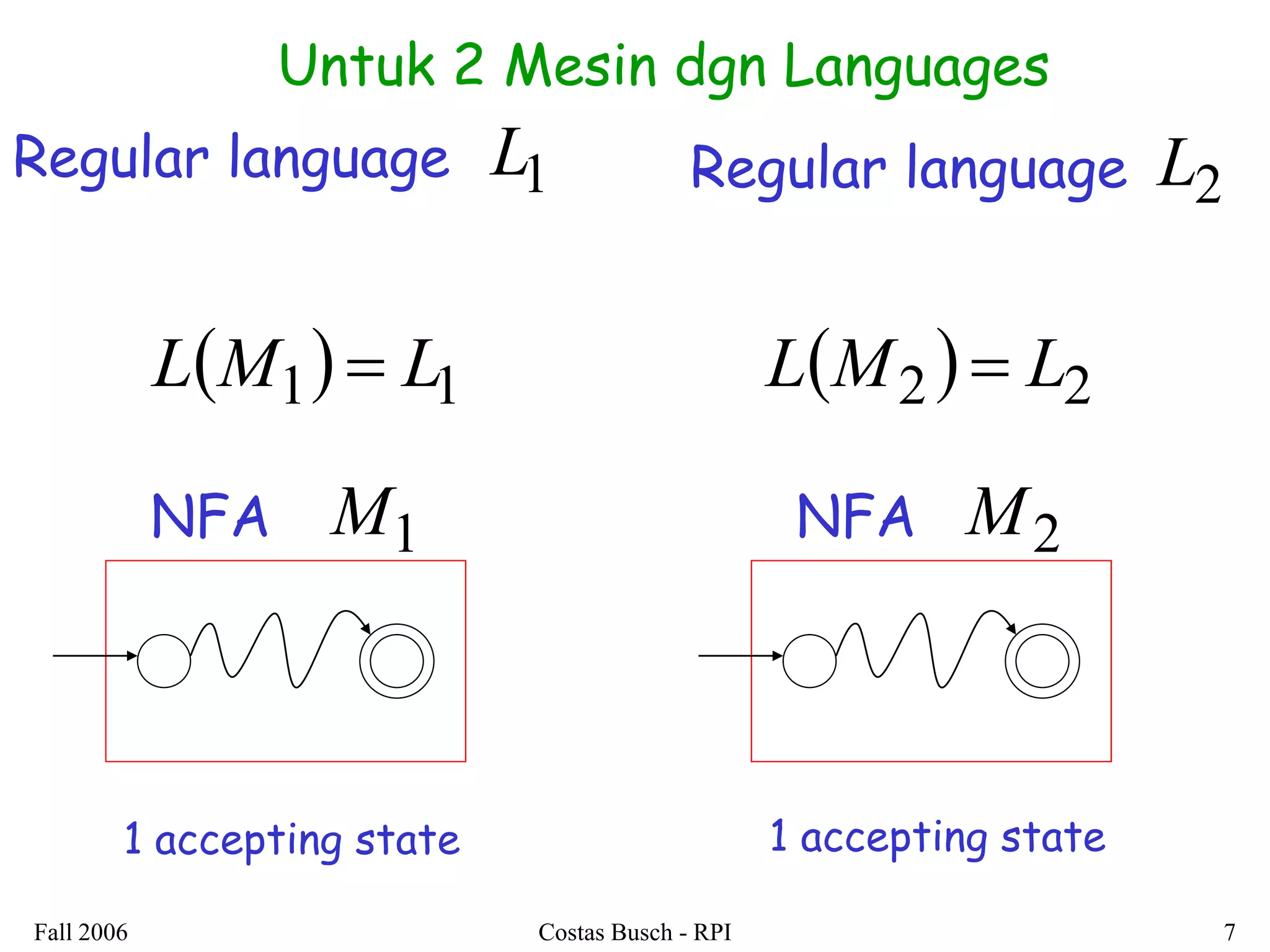
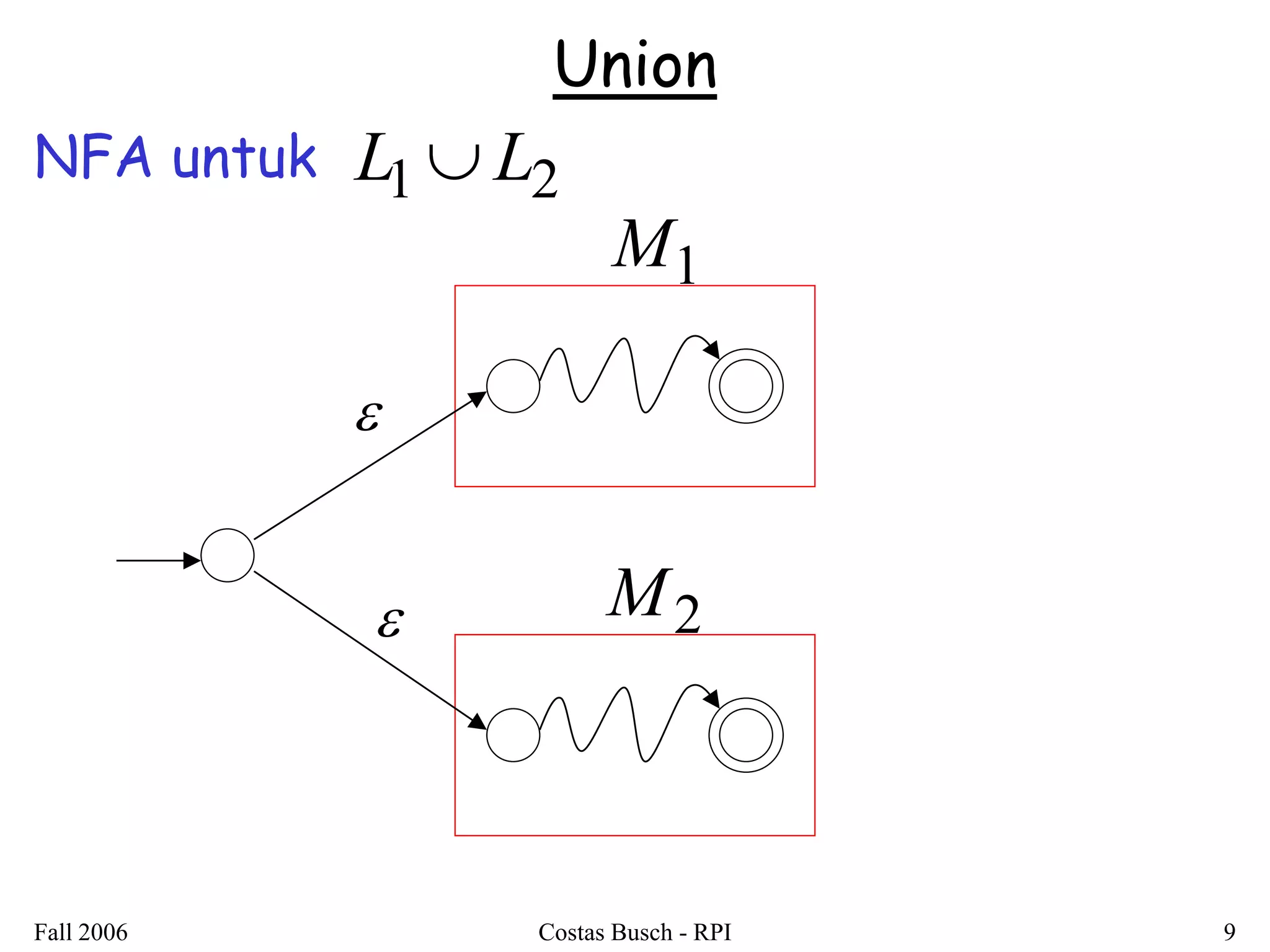
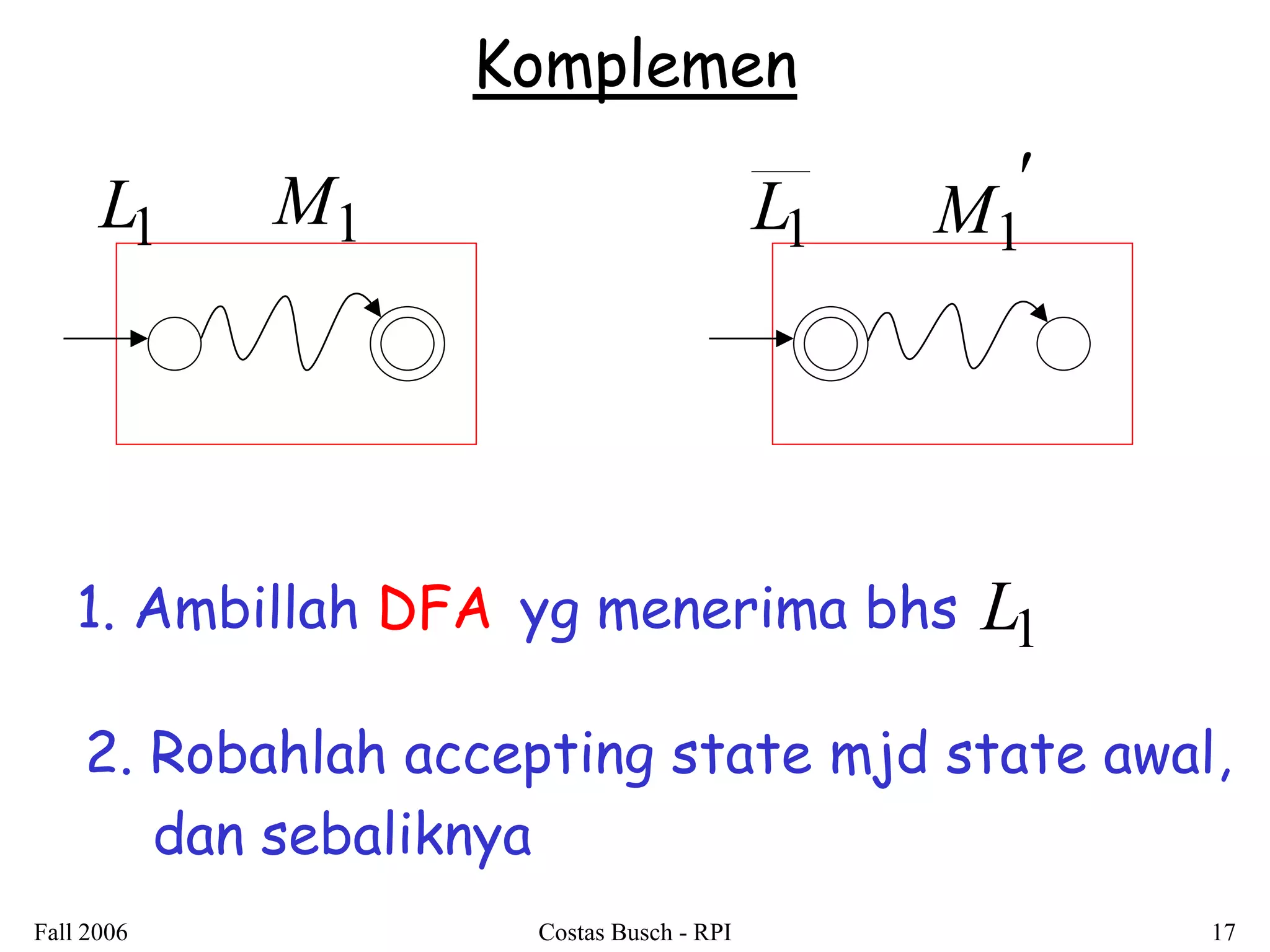
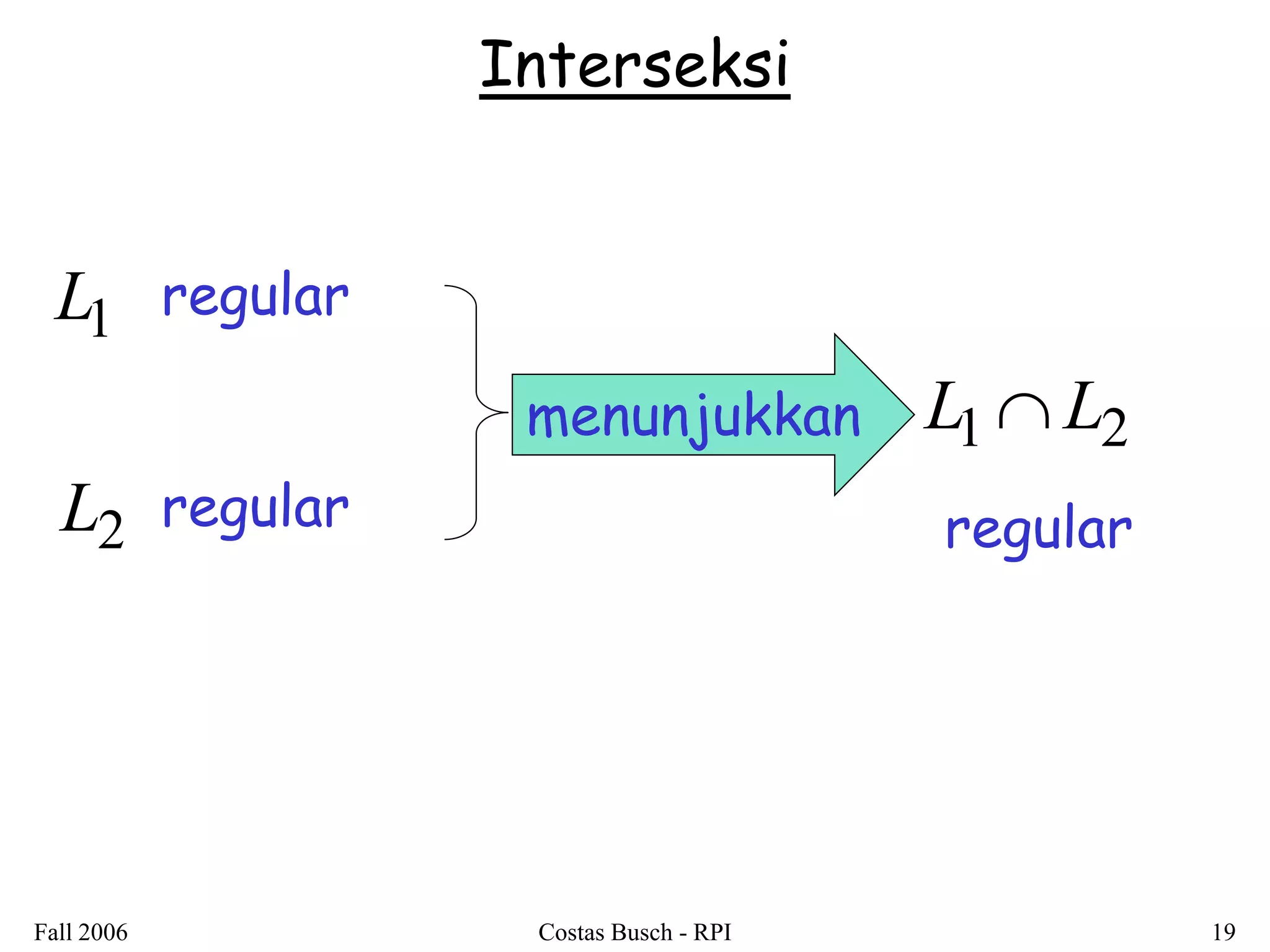
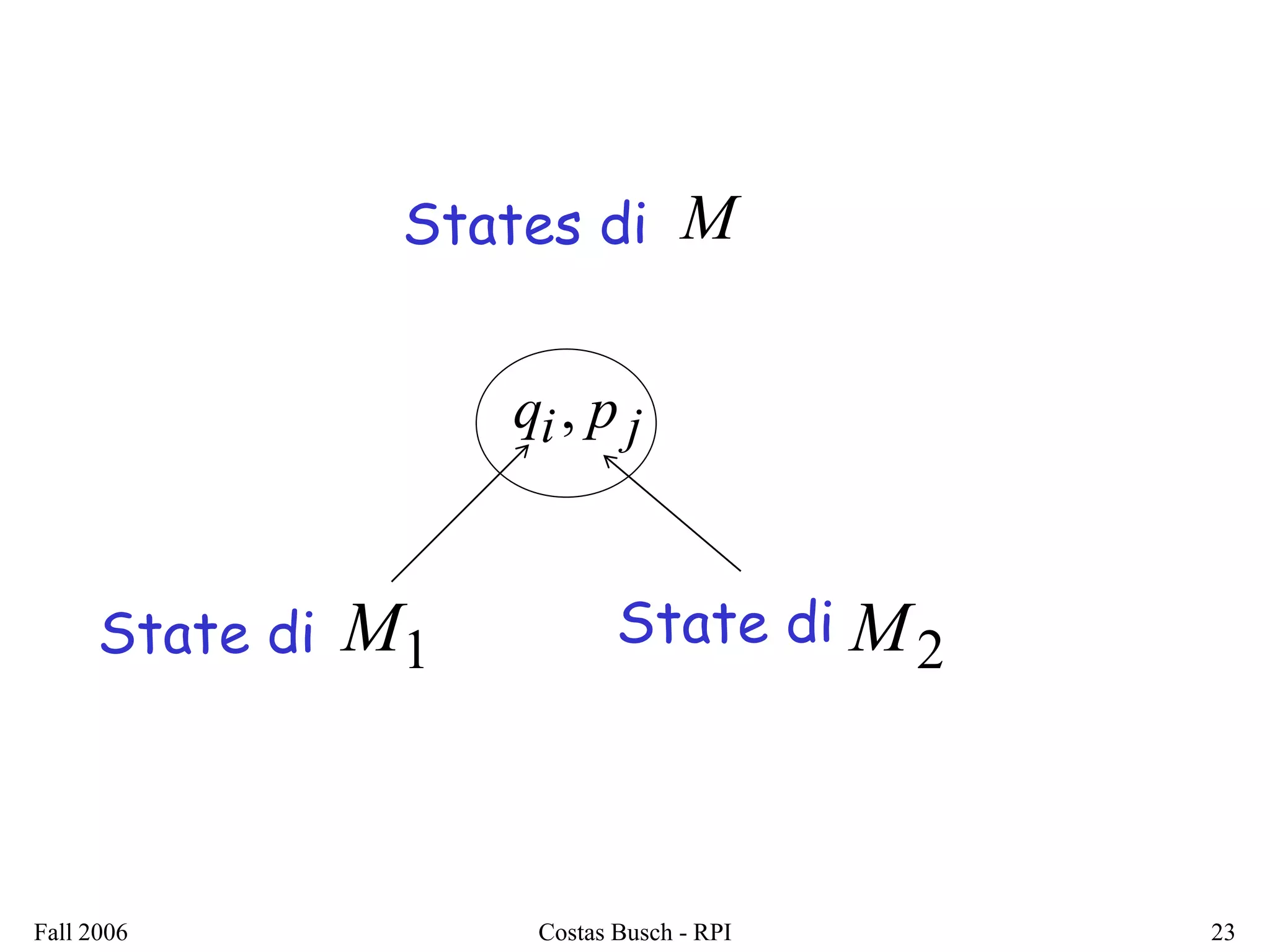
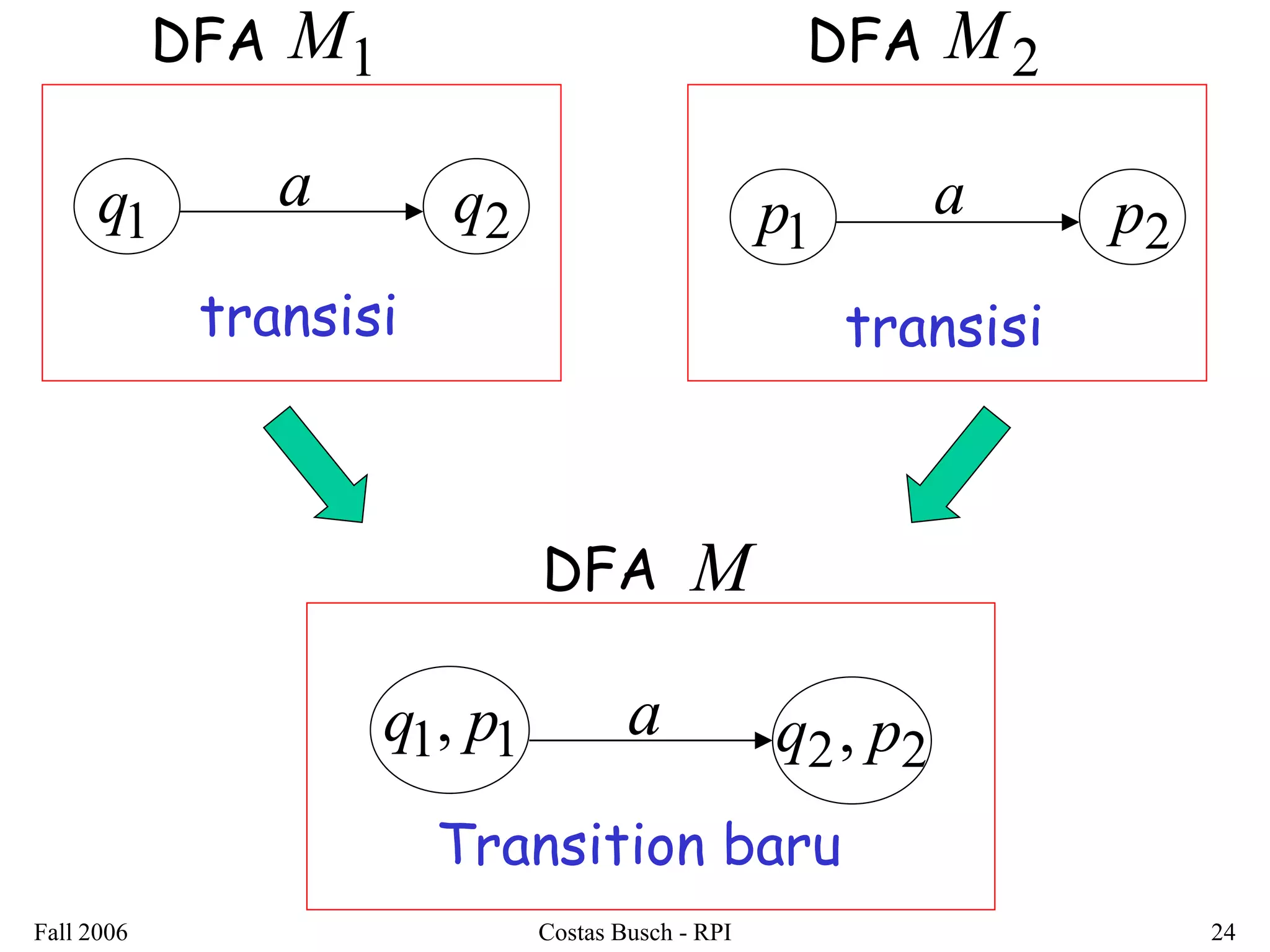
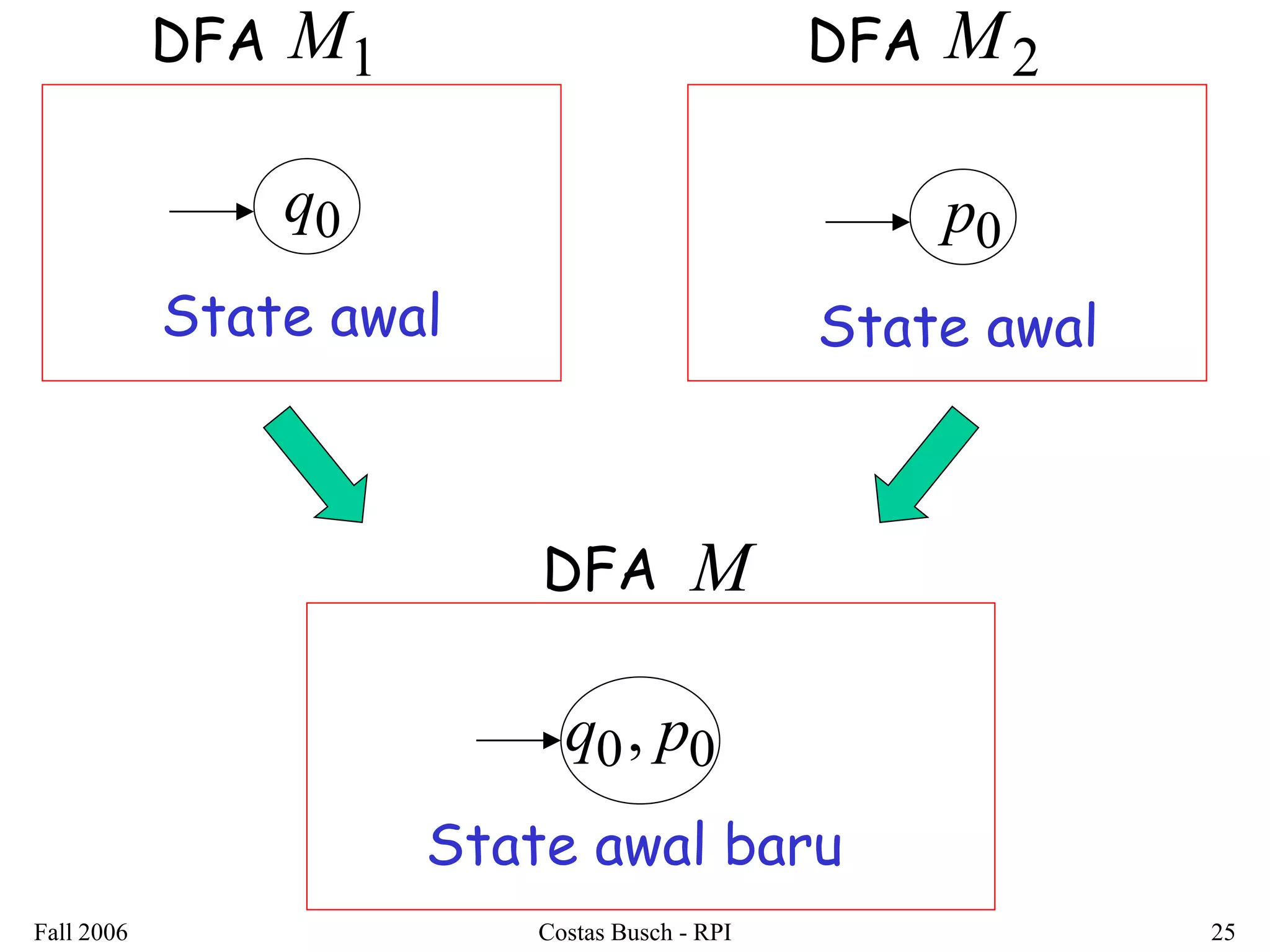
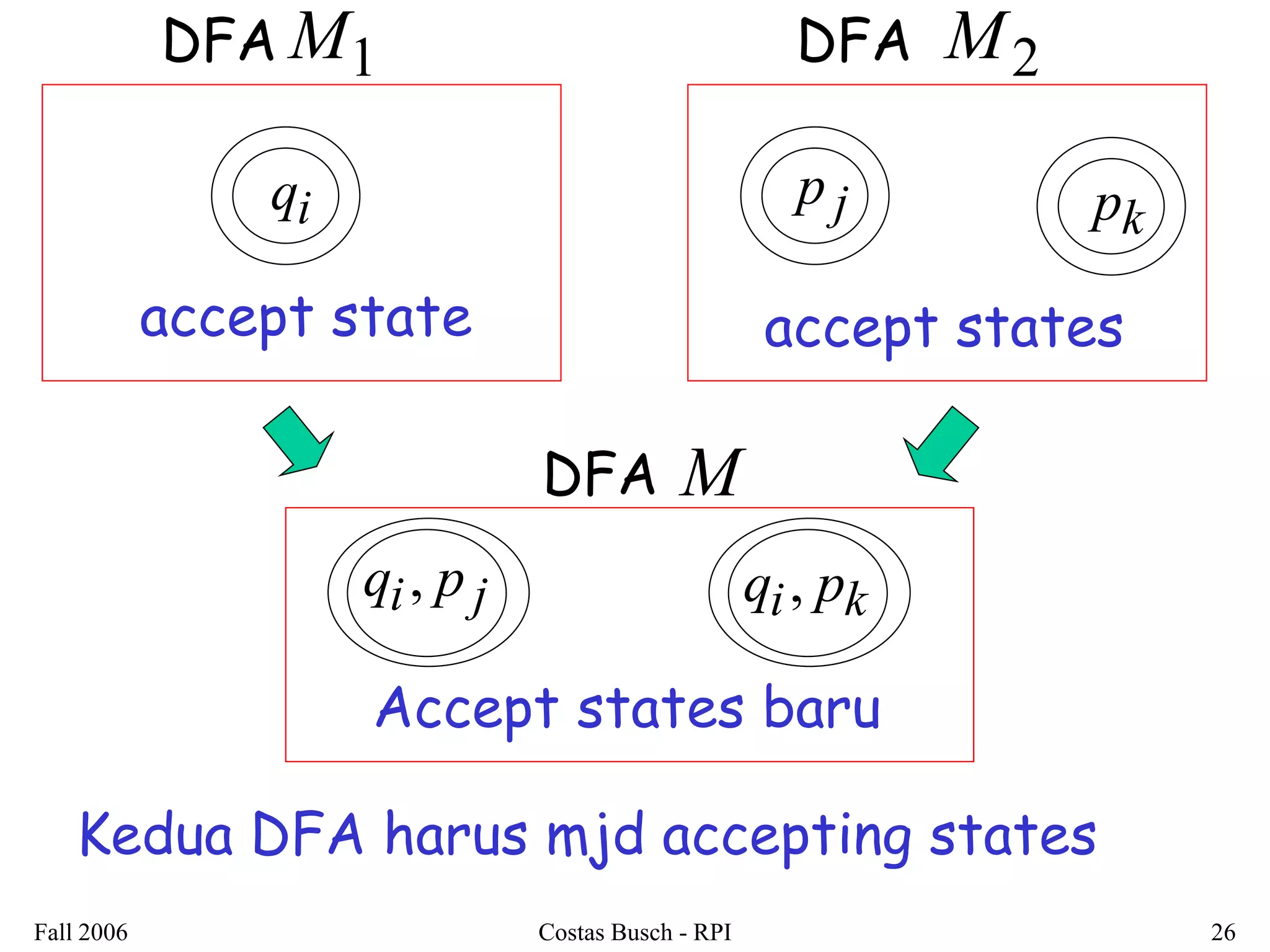
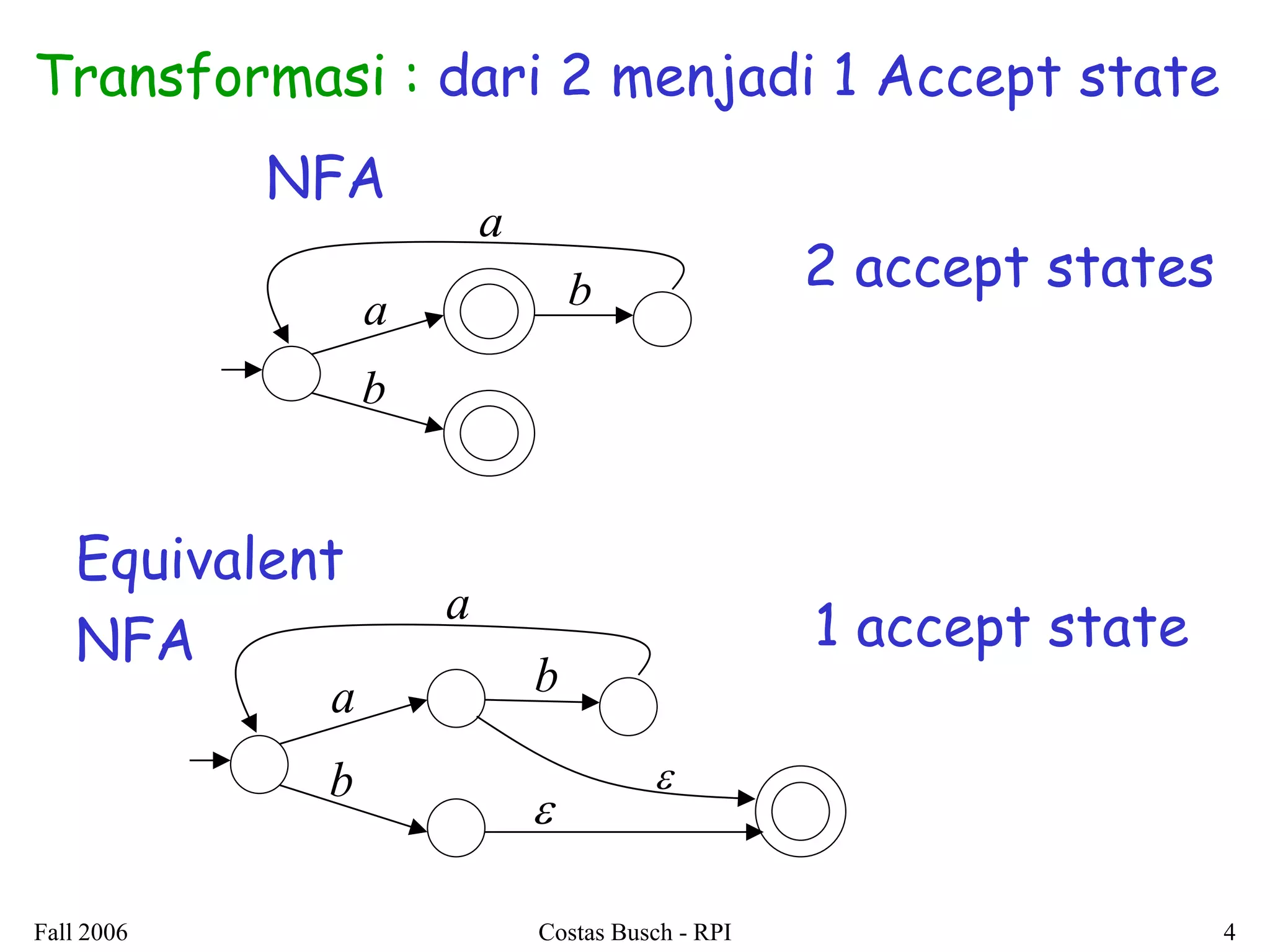
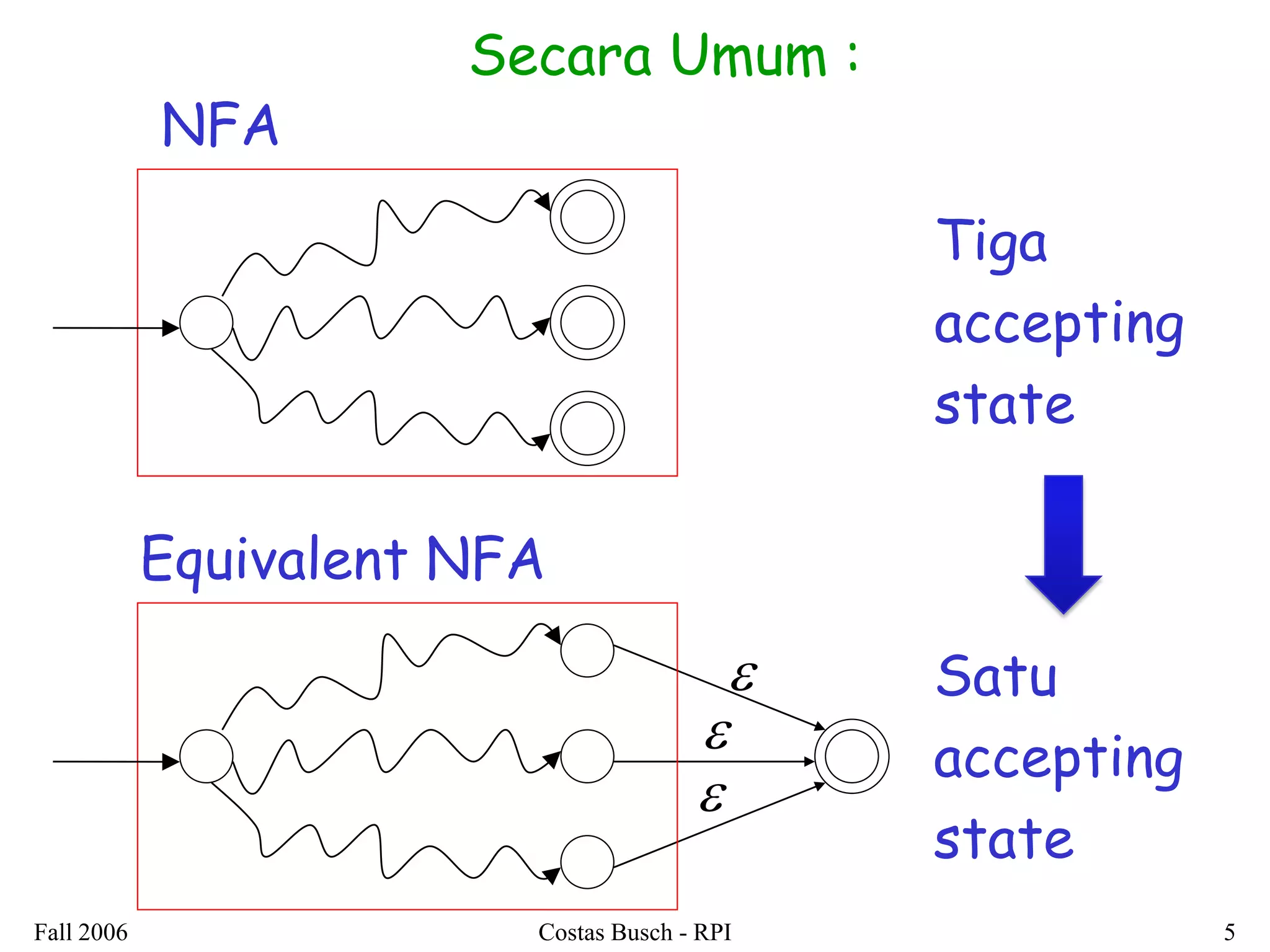
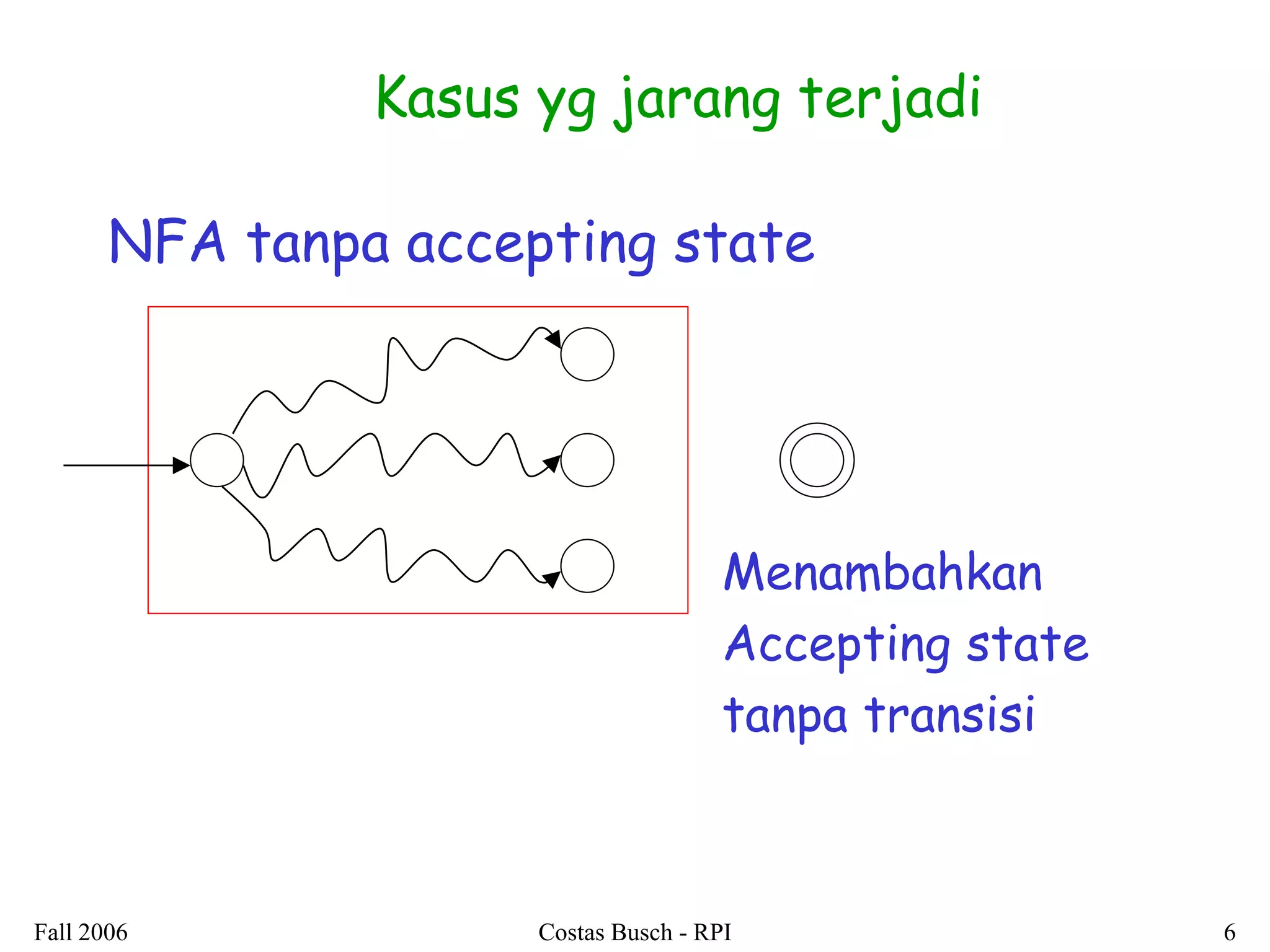
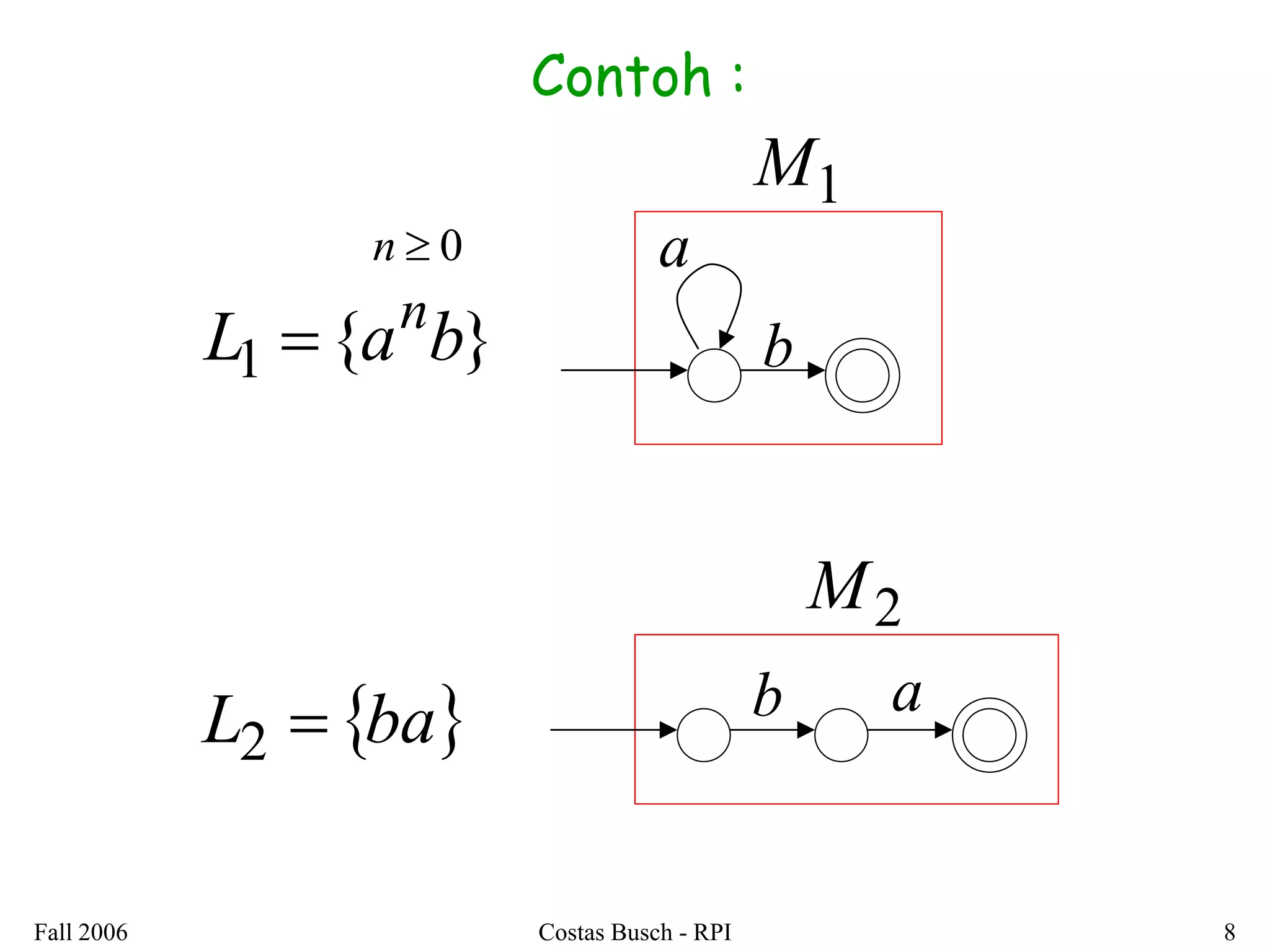
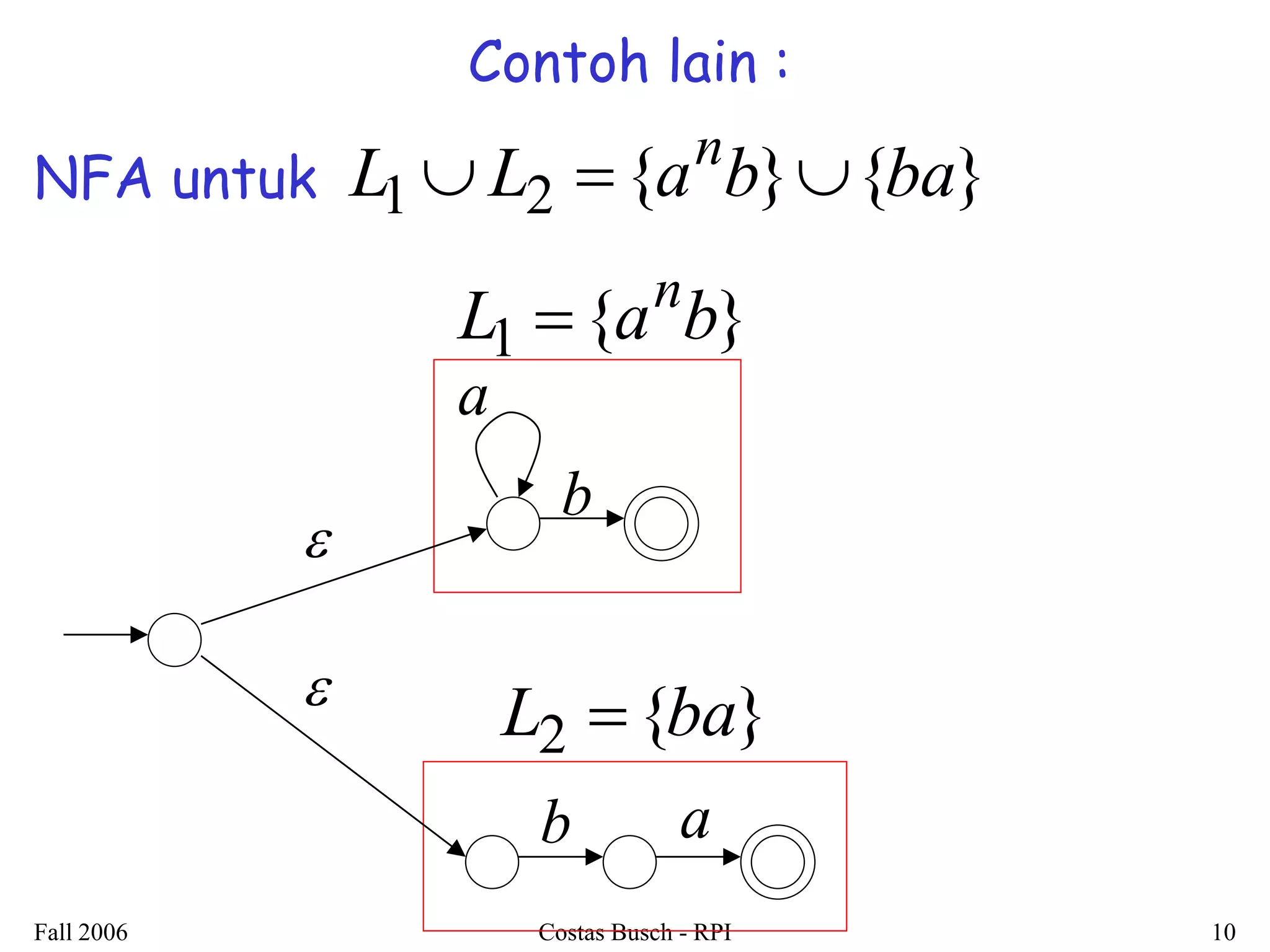
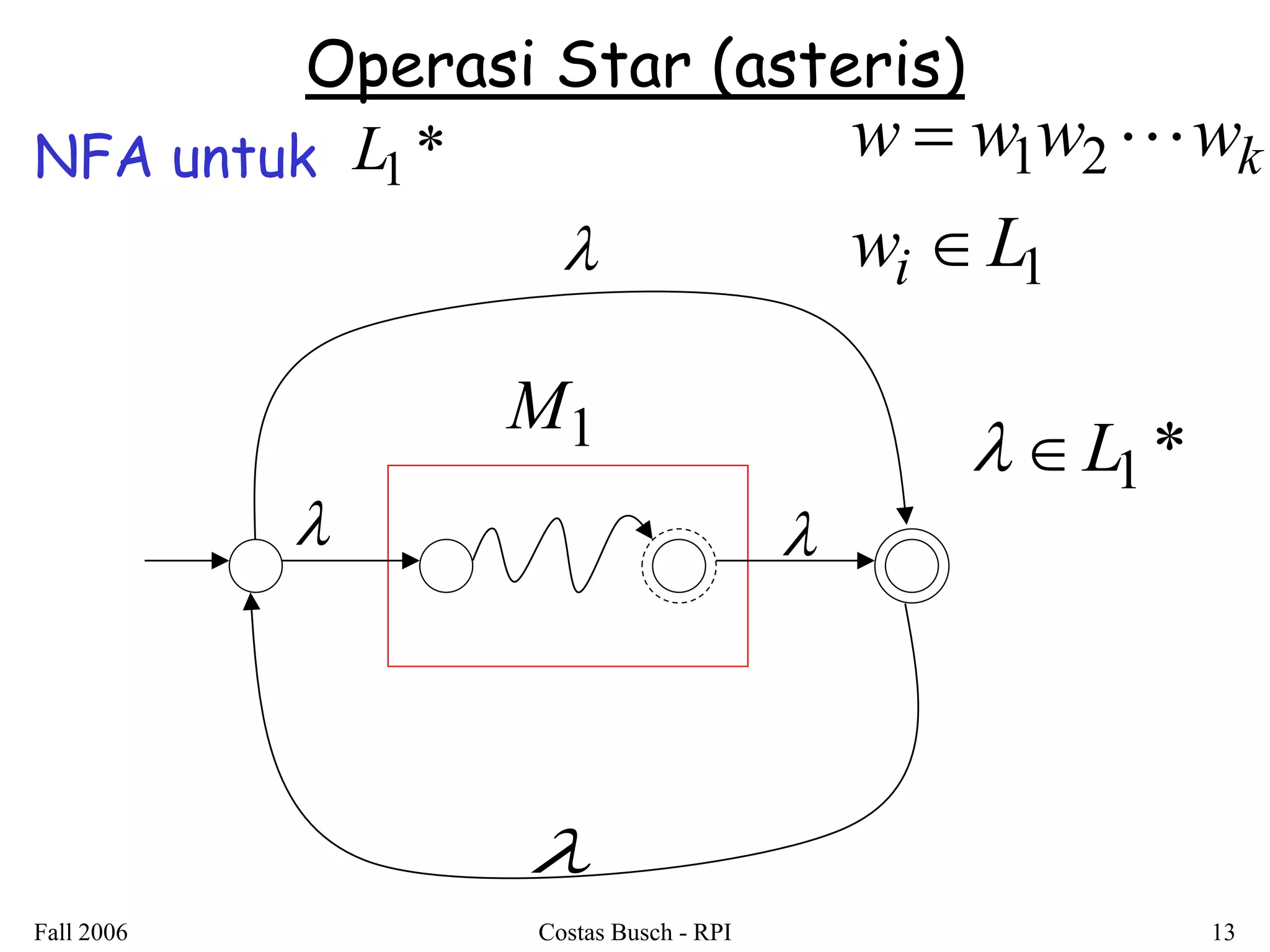
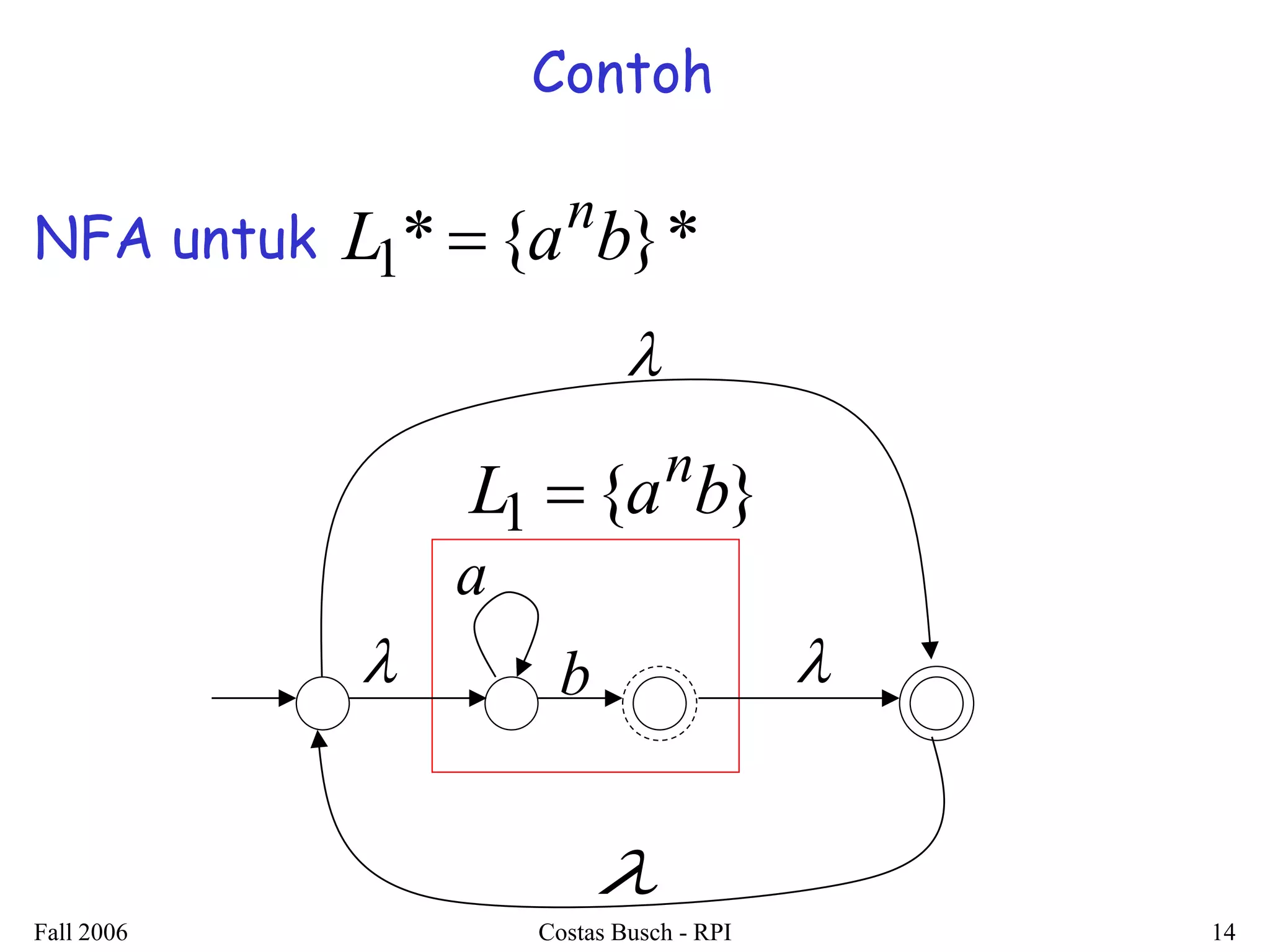
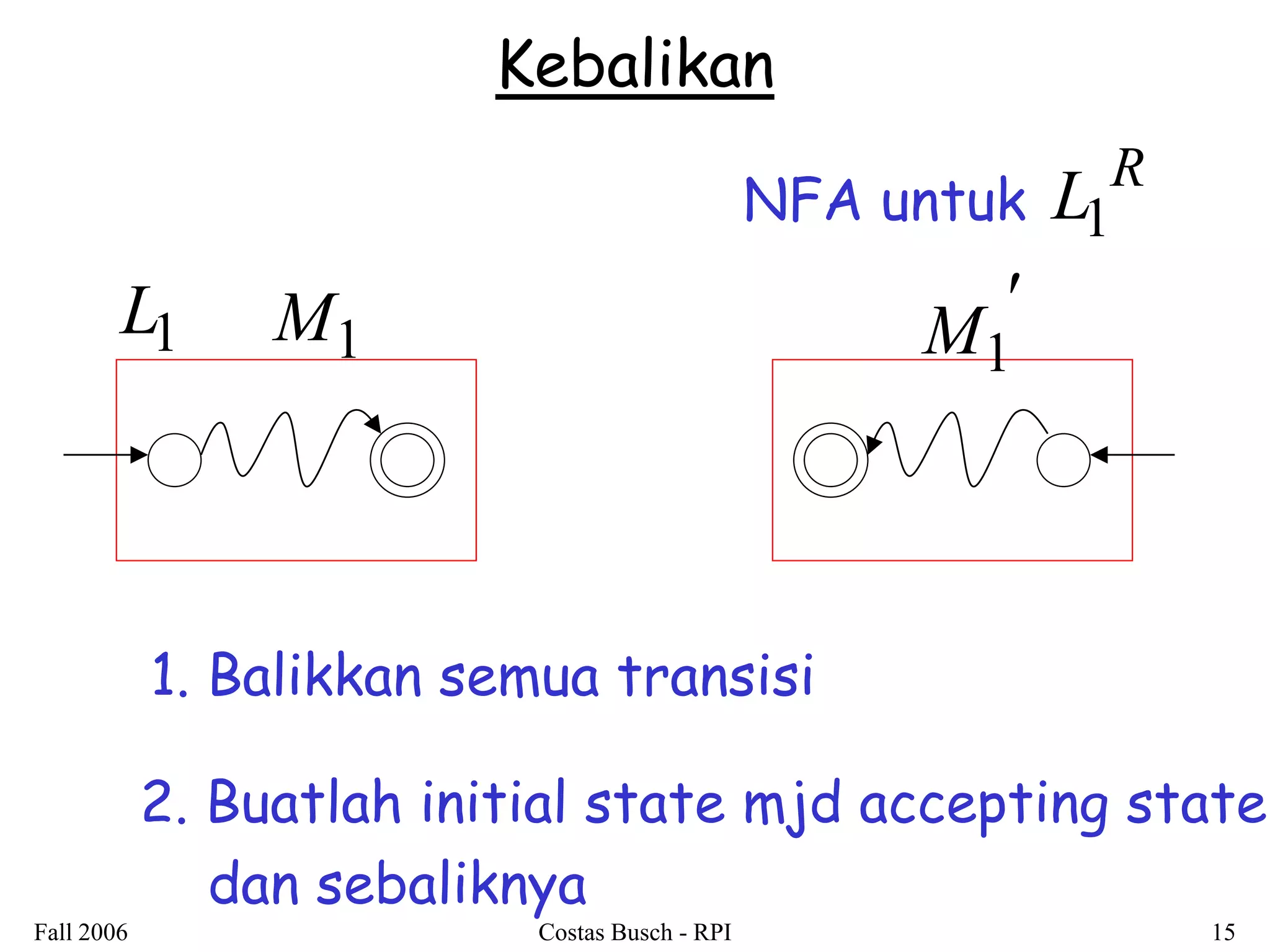
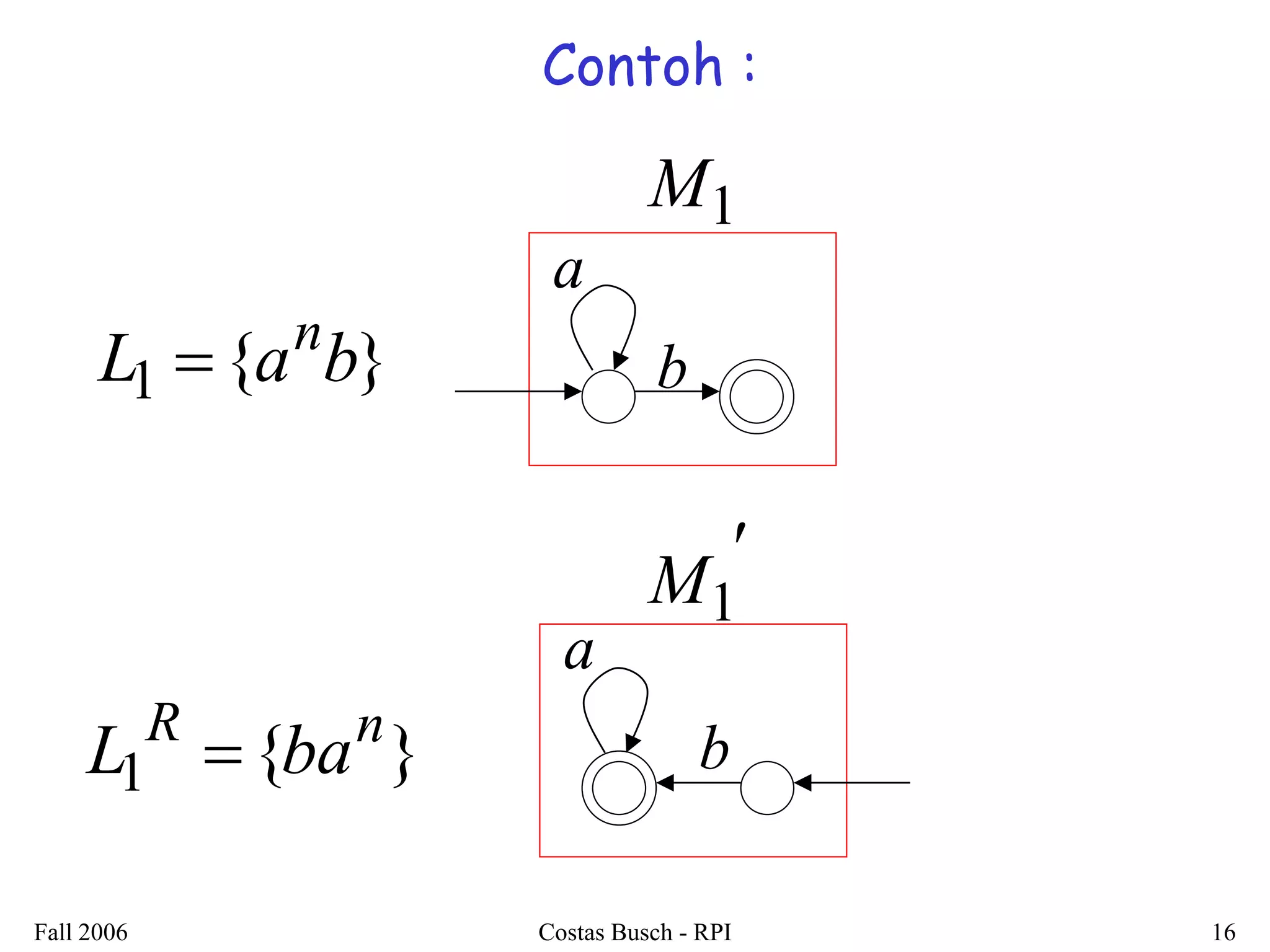
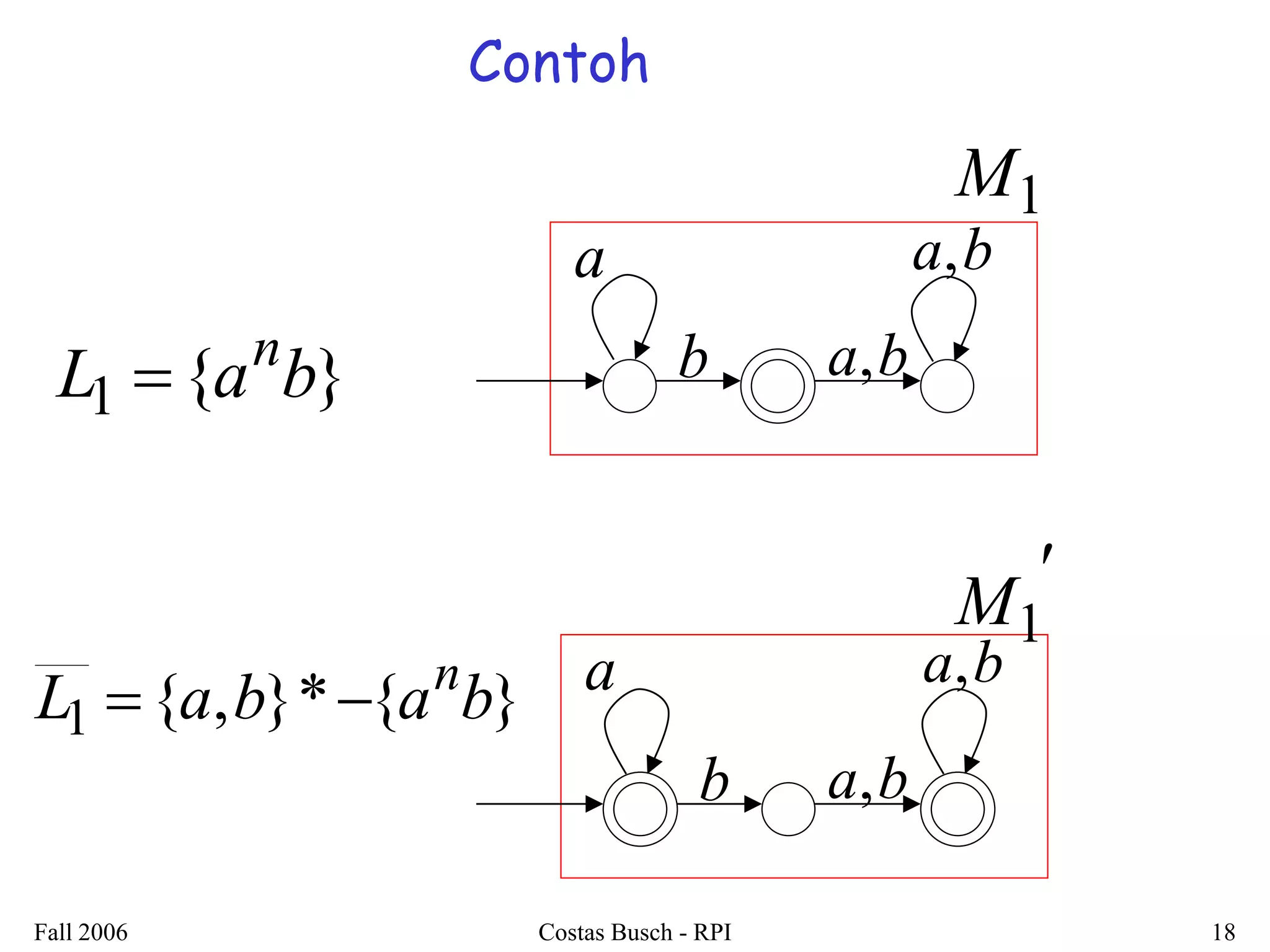
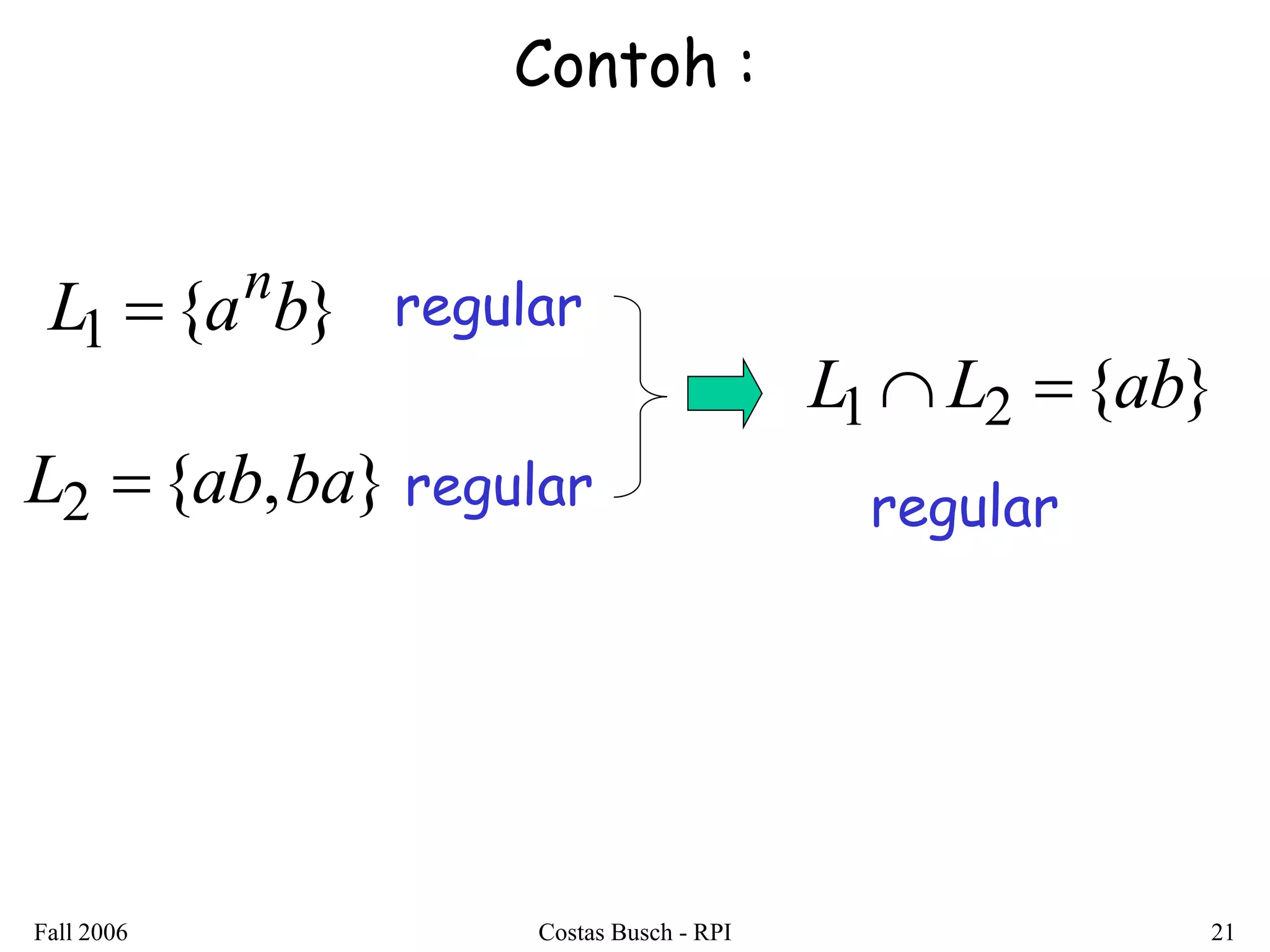
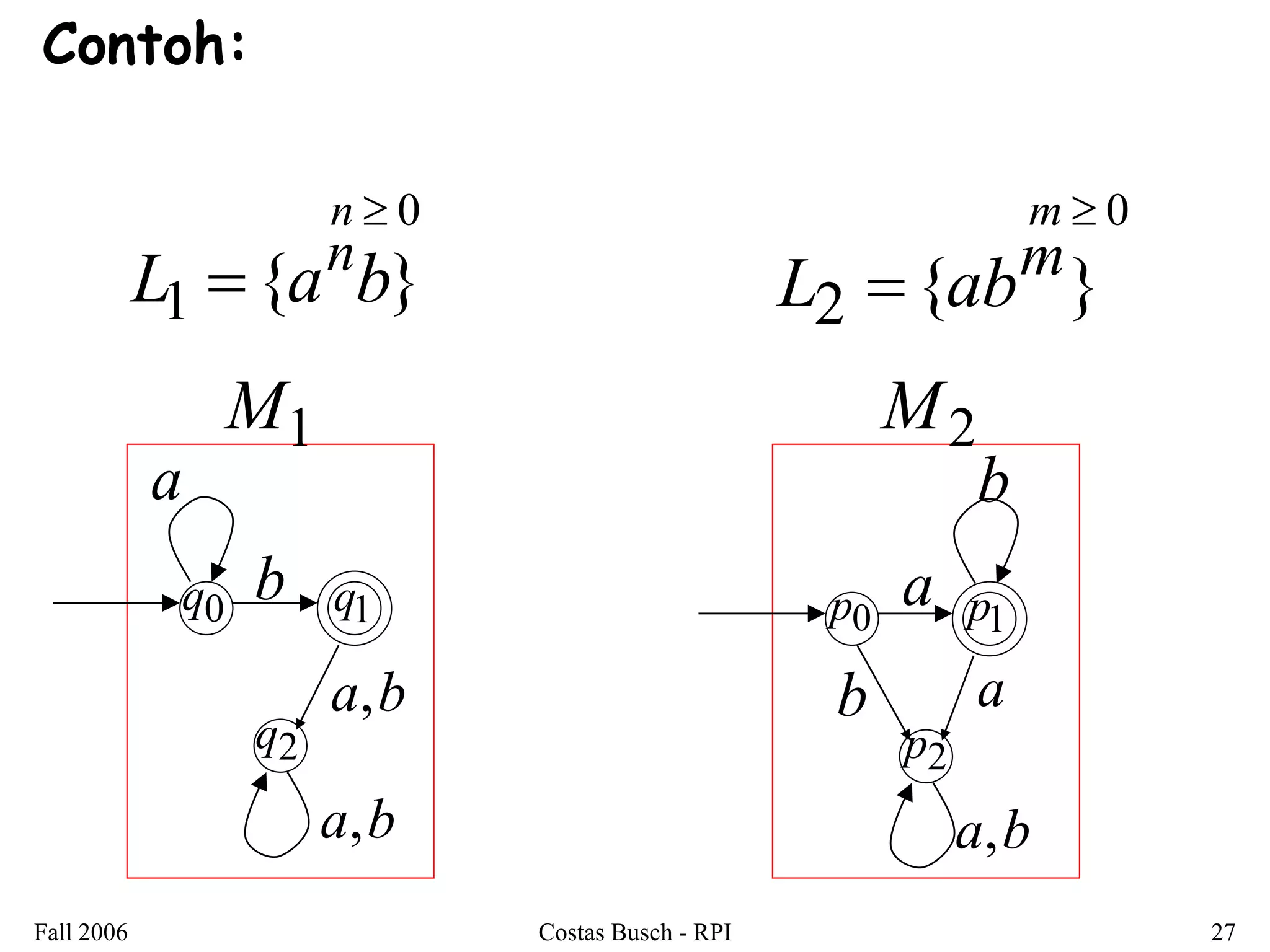
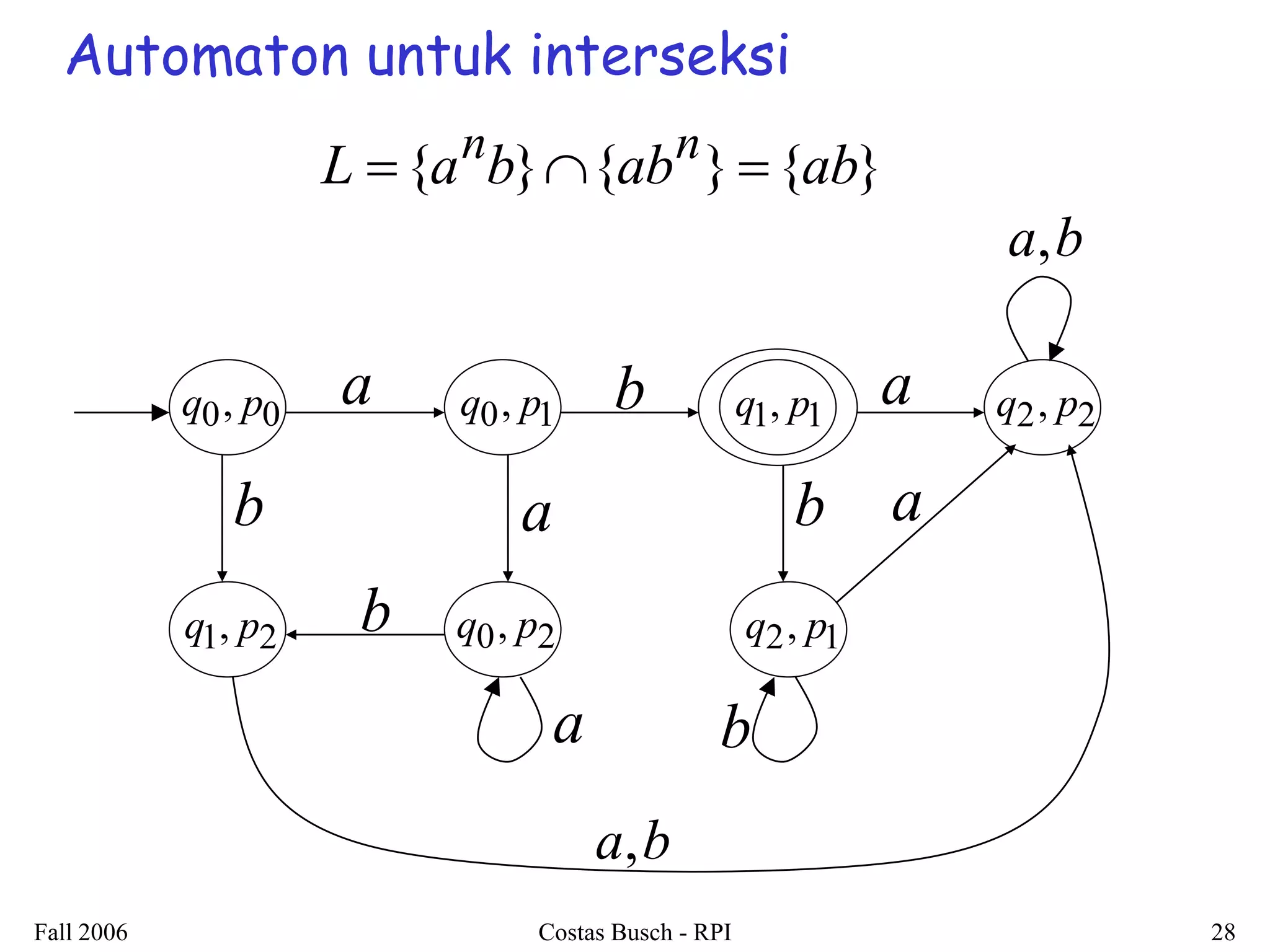
1. The document discusses properties of regular languages and operations on regular languages such as concatenation, union, intersection, complement, reversal, and Kleene star. 2. It is shown that regular languages are closed under these operations - the result of applying these operations to regular languages is also a regular language. 3. Examples are provided to illustrate how to construct non-deterministic finite automata (NFAs) that recognize languages resulting from applying different operations to sample regular languages.

1. Fall 2006
Costas Busch - RPI
1
Sifat-sifat Regular Languages

2. Fall 2006 Costas Busch - RPI 2
L1 L2
Concatenation: L1L2
Star: L1 *
Union: L1L2
Regular
Languages
Untuk regular languages and
Akan dibuktikan bahwa:
L1
L1L2
Complement:
Intersection:
R L1 Reversal:

3. Fall 2006 Costas Busch - RPI 3
Dapat dikatakan : Regular languages
Tertutup untuk operasi-operasi
Concatenation: L1L2
Star: L1 *
Union: L1L2
L1
L1L2
Complement:
Intersection:
R L1 Reversal:

4. Fall 2006 Costas Busch - RPI 4
a
b
b
a
NFA
Equivalent
NFA


a
b
b
a
Transformasi : dari 2 menjadi 1 Accept state
2 accept states
1 accept state

5. Fall 2006 Costas Busch - RPI 5
NFA
Equivalent NFA
Satu
accepting
state

Secara Umum :
Tiga
accepting
state



6. Fall 2006
Costas Busch - RPI
6
NFA tanpa accepting state
Menambahkan
Accepting state
tanpa transisi
Kasus yg jarang terjadi

7. Fall 2006 Costas Busch - RPI 7
Regular language L1
LM1  L1
M1
1 accepting state
NFA M2
L2
1 accepting state
LM2   L2
Regular language
NFA
Untuk 2 Mesin dgn Languages

8. Fall 2006 Costas Busch - RPI 8
L1 {a b} n 
a
b
M1
L2  ba
b a
M2
n  0
Contoh :

9. Fall 2006 Costas Busch - RPI 9
Union
NFA untuk
M1
M2
L1L2



10. Fall 2006 Costas Busch - RPI 10
a
b
b a
L1 {a b} n 
L2 {ba}
L1 L2 {a b} {ba} n NFA untuk   
Contoh lain :



11. Fall 2006 Costas Busch - RPI 11
Concatenation
NFA untuk L1L2
M1 M2


12. Fall 2006 Costas Busch - RPI 12
NFA untuk
a
b b a
L1 {a b} n 
L2 {ba}
L1L2 {a b}{ba} {a bba} n n  
Contoh :


13. Fall 2006 Costas Busch - RPI 13
Operasi Star (asteris)
NFA untuk L1 *
M1


 L1*
 
1
1 2
w L
w w w w
i
k

 

14. Fall 2006 Costas Busch - RPI 14
NFA untuk L1* {a b}* n 
a
b
L1 {a b} n 




Contoh

15. Fall 2006 Costas Busch - RPI 15
Kebalikan
R L1
M1
NFA untuk

M1
1. Balikkan semua transisi
2. Buatlah initial state mjd accepting state
dan sebaliknya
L1

16. Fall 2006 Costas Busch - RPI 16
L1 {a b} n 
a
b
M1
1 { }
R n L  ba
a
b

M1
Contoh :

17. Fall 2006 Costas Busch - RPI 17
Komplemen
1. Ambillah DFA yg menerima bhs L 1
L1 M1 
L1 M1
2. Robahlah accepting state mjd state awal,
dan sebaliknya

18. Fall 2006 Costas Busch - RPI 18
L1 {a b} n 
a
b
M1
a,b
a,b
L1 {a,b}* {a b} n   a
b

M1
a,b
a,b
Contoh

19. Fall 2006 Costas Busch - RPI 19
Interseksi
L1 regular
L2 regular
menunjukkan L1L2
regular

20. Fall 2006 Costas Busch - RPI 20
Hukum DeMorgan’s : L1L2  L1L2
L1 , L2 regular
L1 , L2 regular
L1L2 regular
L1L2 regular
L1L2 regular

21. Fall 2006 Costas Busch - RPI 21
Contoh :
L1 {a b} n 
L2 {ab,ba}
regular
regular
L1L2 {ab}
regular

22. Fall 2006 Costas Busch - RPI 22
DFA utk L1 utk L2
M1
DFA
M2
Buatlah DFA yg baru dgn bhs yg diterima
Mesin Mesin
M
L1L2
M Mensimulasikan scr paralel M 1 dan M2
Pembuktian lain utk Closure Interseksi

23. Fall 2006 Costas Busch - RPI 23
States di M
qi , p j
State di M1 State di M2

24. Fall 2006 Costas Busch - RPI 24
M1 M2
q1 q2 a
transisi
p1 p2 a
transisi
DFA DFA
q1, p1 a
Transition baru
DFA M
q2, p2

25. Fall 2006 Costas Busch - RPI 25
q0
State awal
p0
State awal
State awal baru
q0, p0
DFA M1 DFA M2
DFA M

26. Fall 2006 Costas Busch - RPI 26
qi
accept state
p j
accept states
Accept states baru
qi , p j
pk
qi , pk
DFA M1 DFA M2
DFA M
Kedua DFA harus mjd accepting states

27. Fall 2006 Costas Busch - RPI 27
Contoh:
L1 {a b} n 
a
b
M1
n  0
2 { }
m L  ab
b
b
M2
q0 q1
p0 p1
m  0
q2
p2
a
a
a,b a,b
a,b

28. Fall 2006 Costas Busch - RPI 28
q0, p0
Automaton untuk interseksi
L {a b} {ab } {ab} n n   
a q0, p1
q1, p2
b
b a q1, p1
q0, p2
a
q2, p1
q2, p2
b
a,b
a
b
a,b
b
a

29. Fall 2006 Costas Busch - RPI 29
M simulates in parallel M 1 and M2
M accepts string w if and only if:
M1 accepts string w
and M 2 accepts string w
L(M)  L(M1)L(M2)