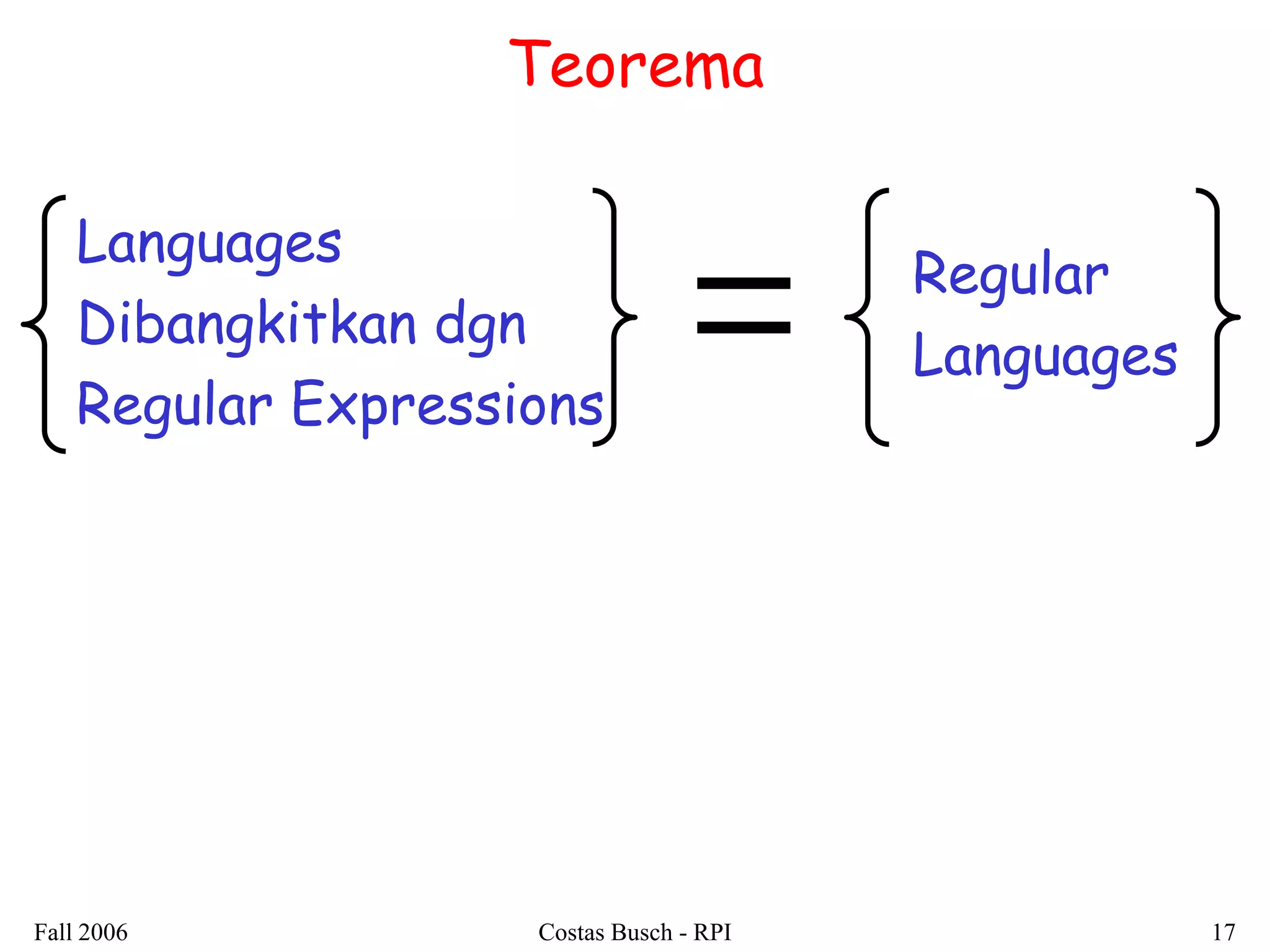
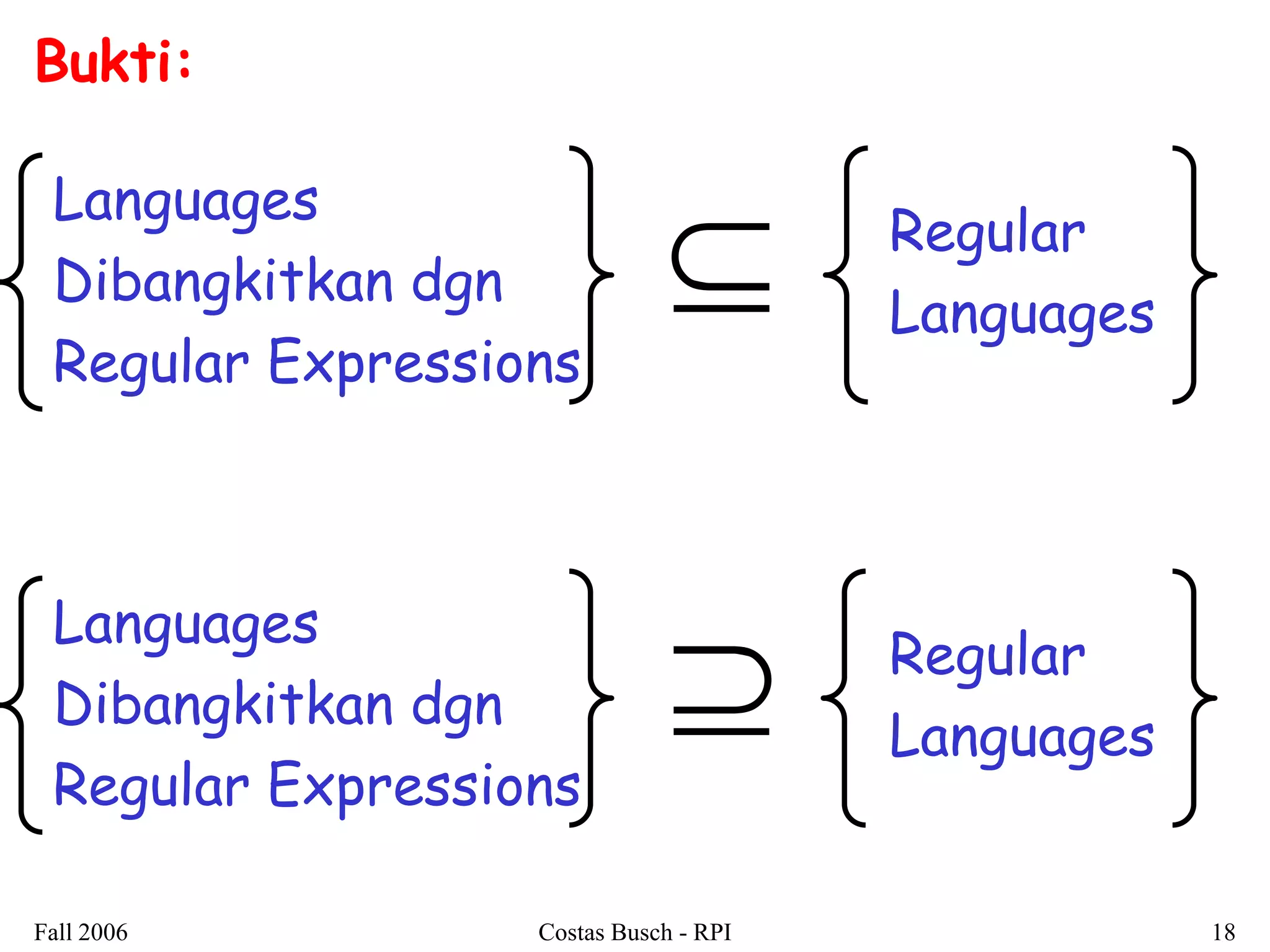
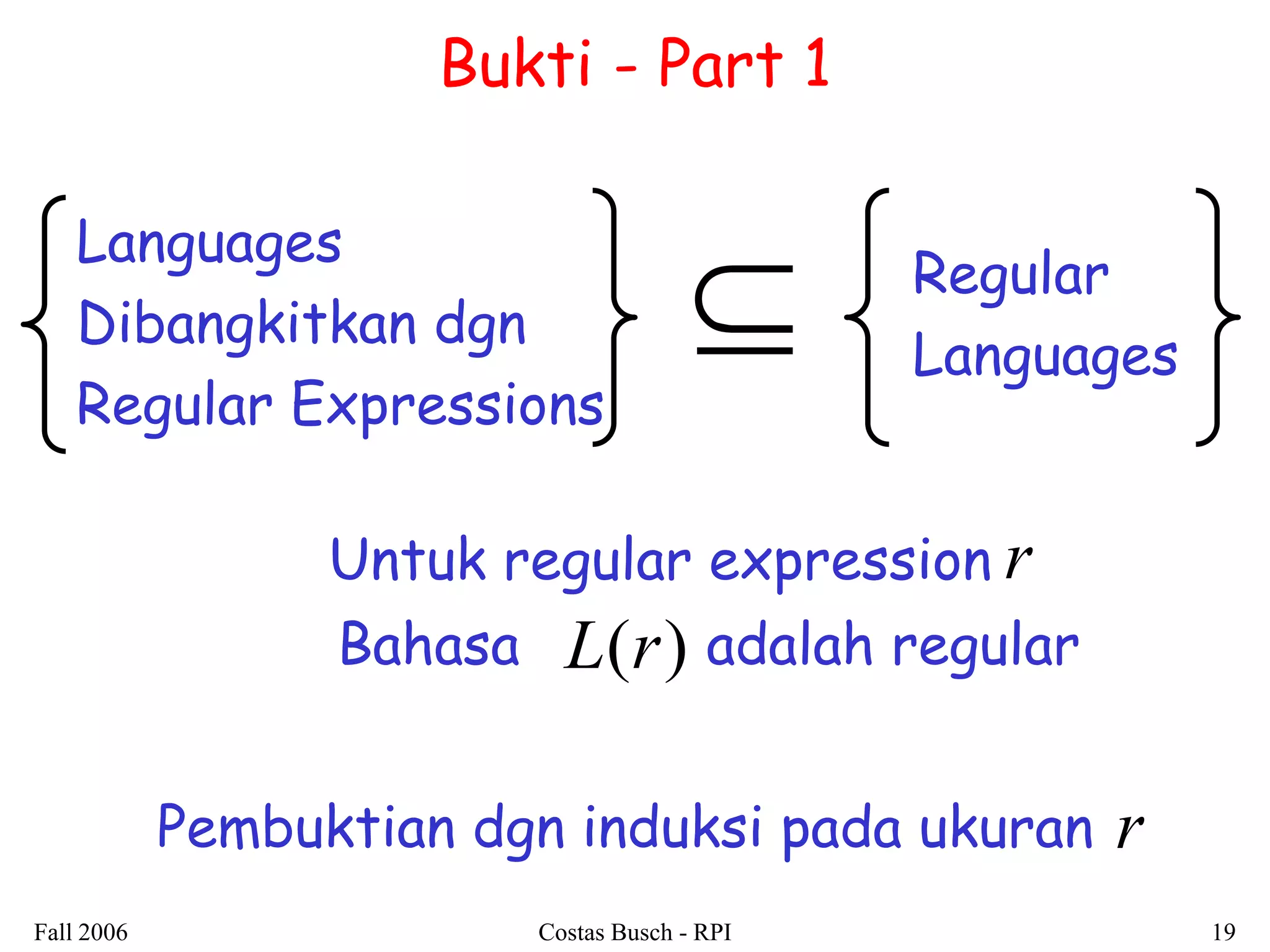
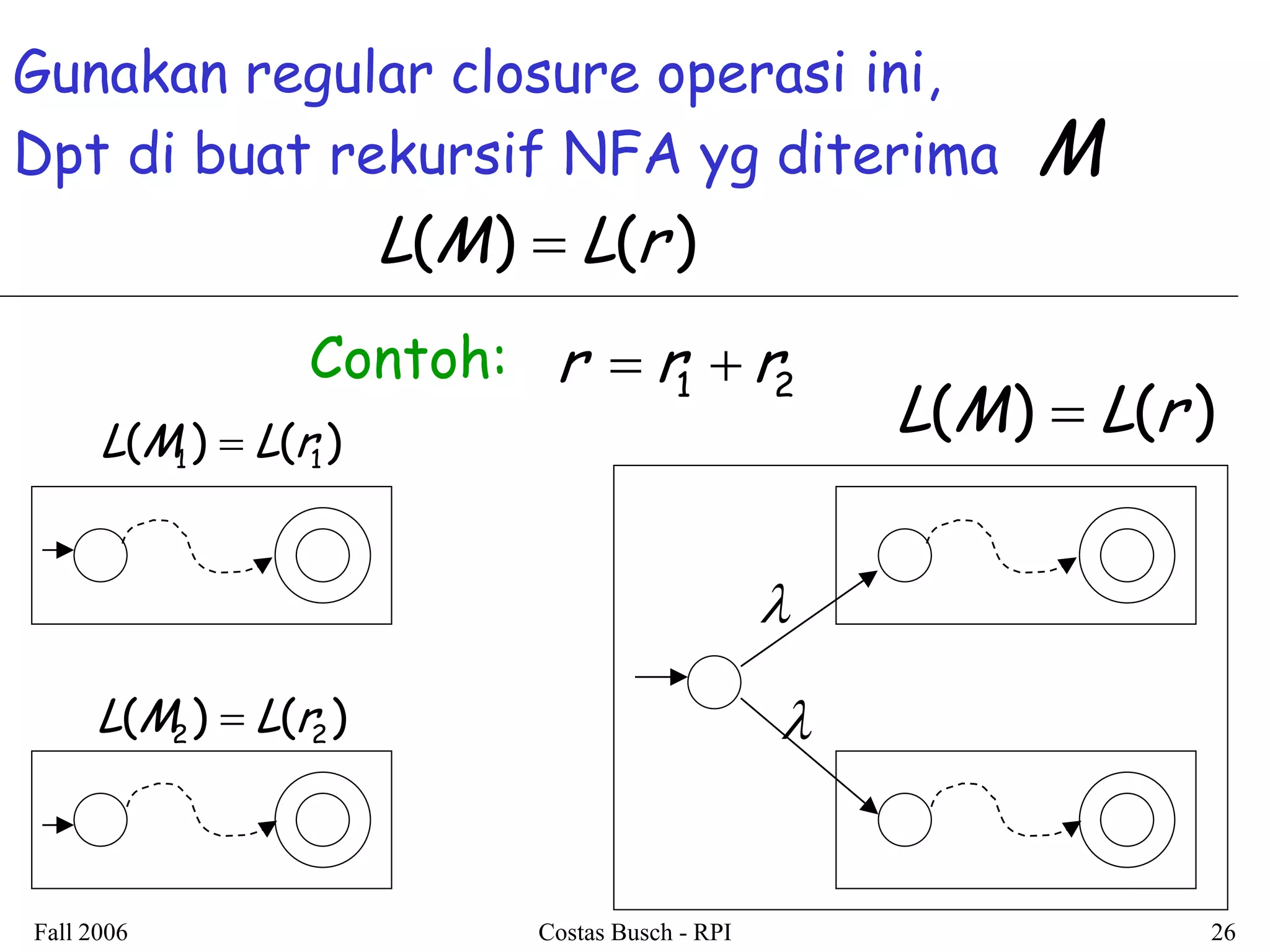
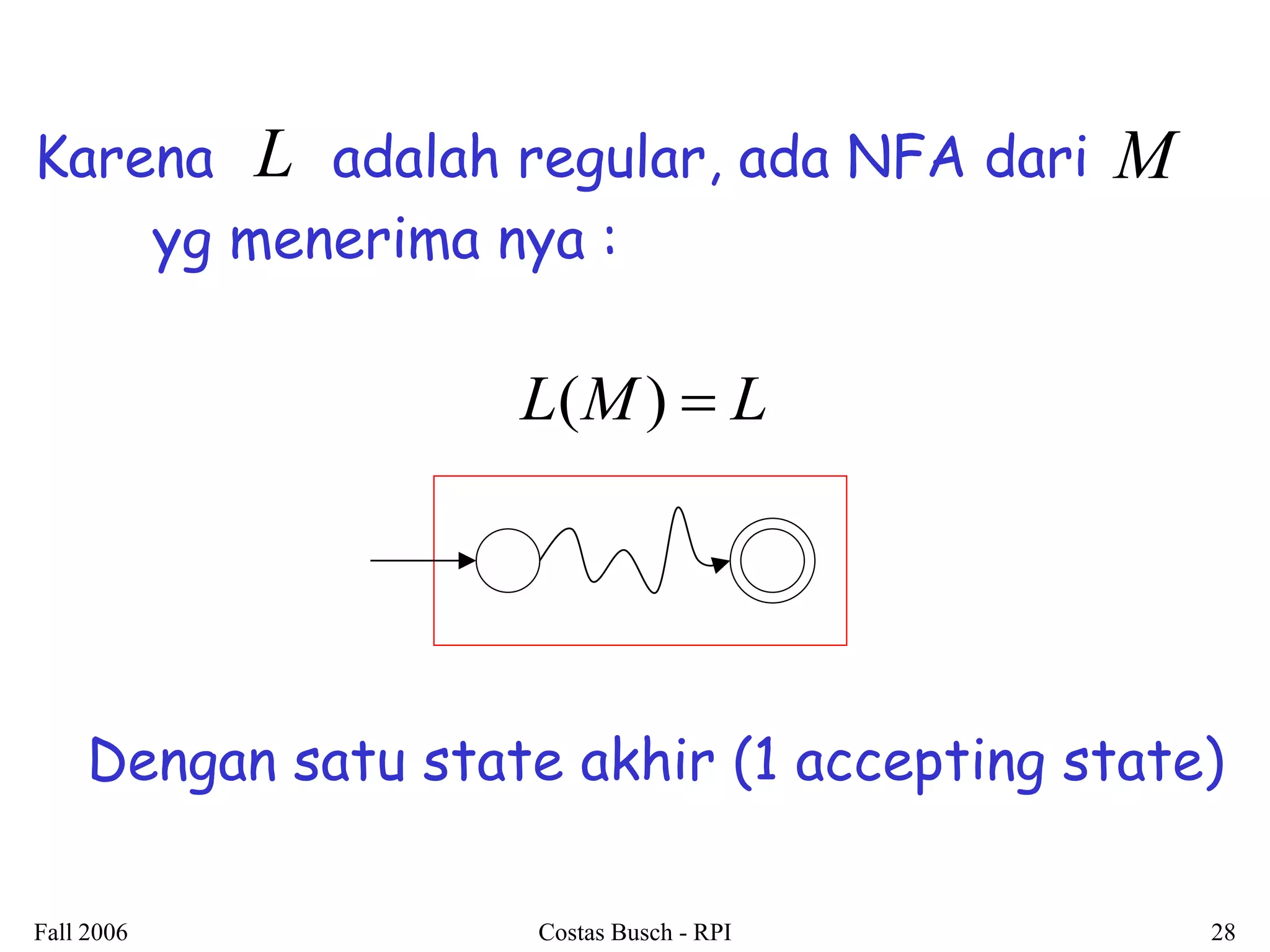
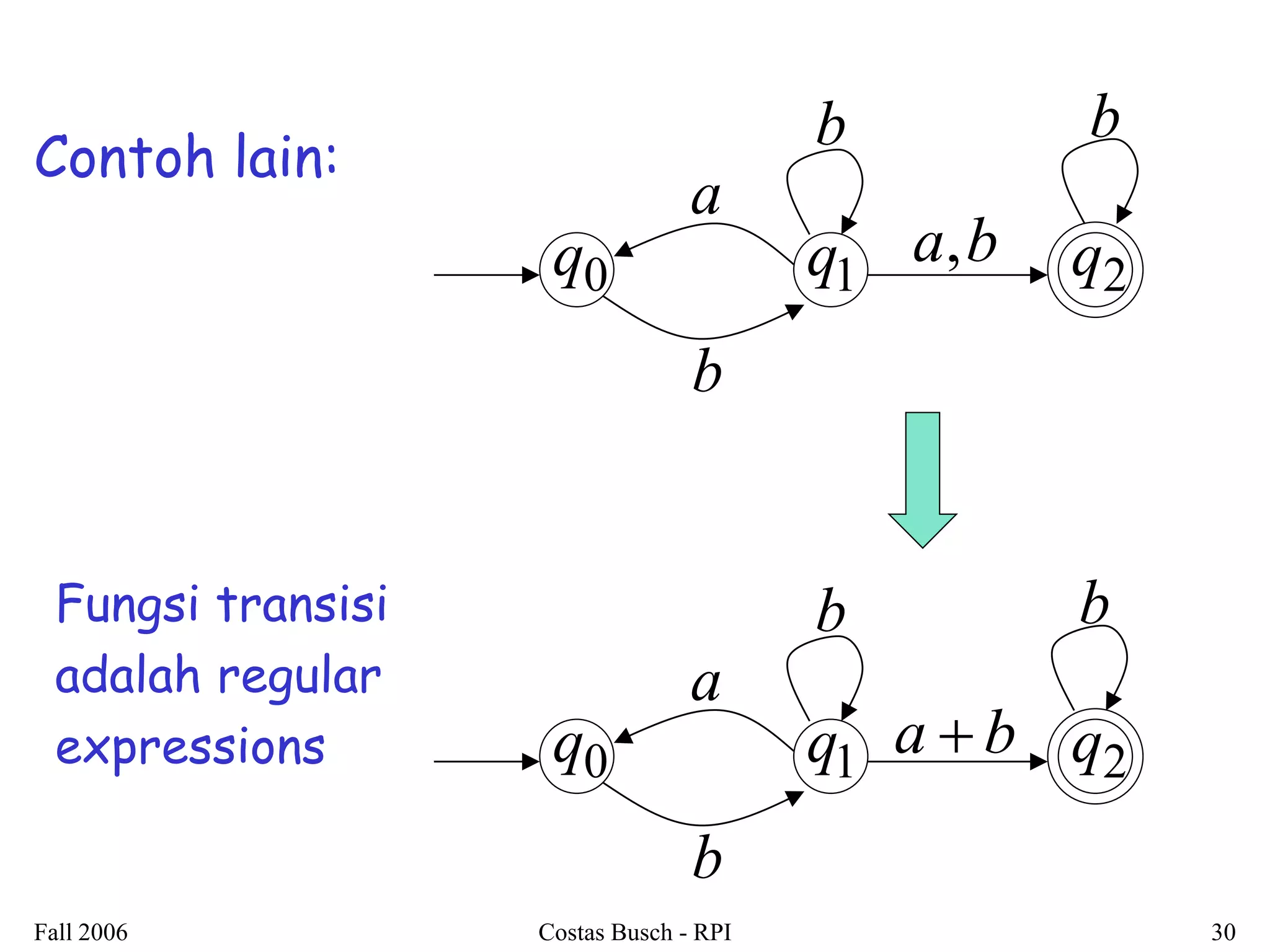
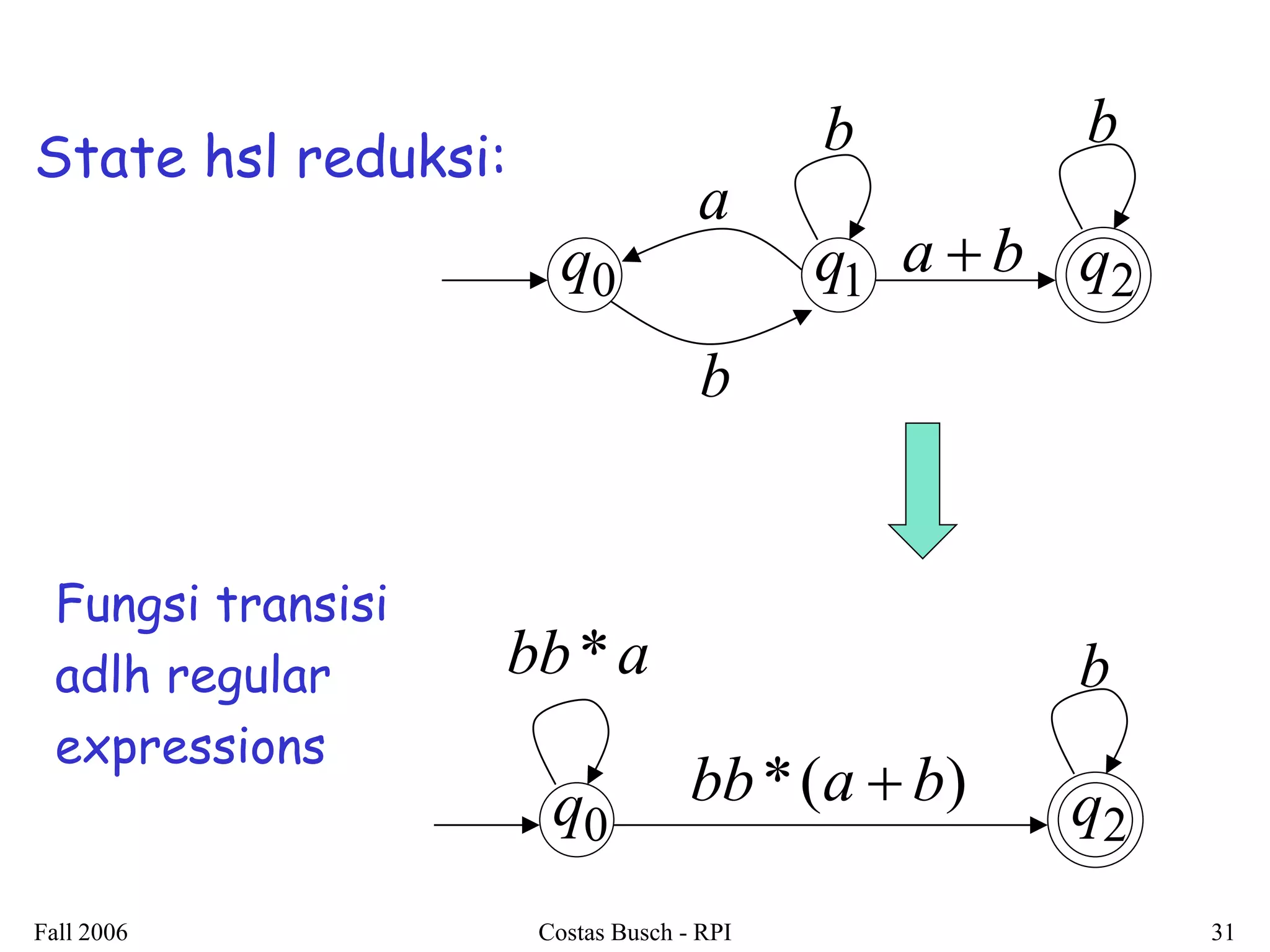
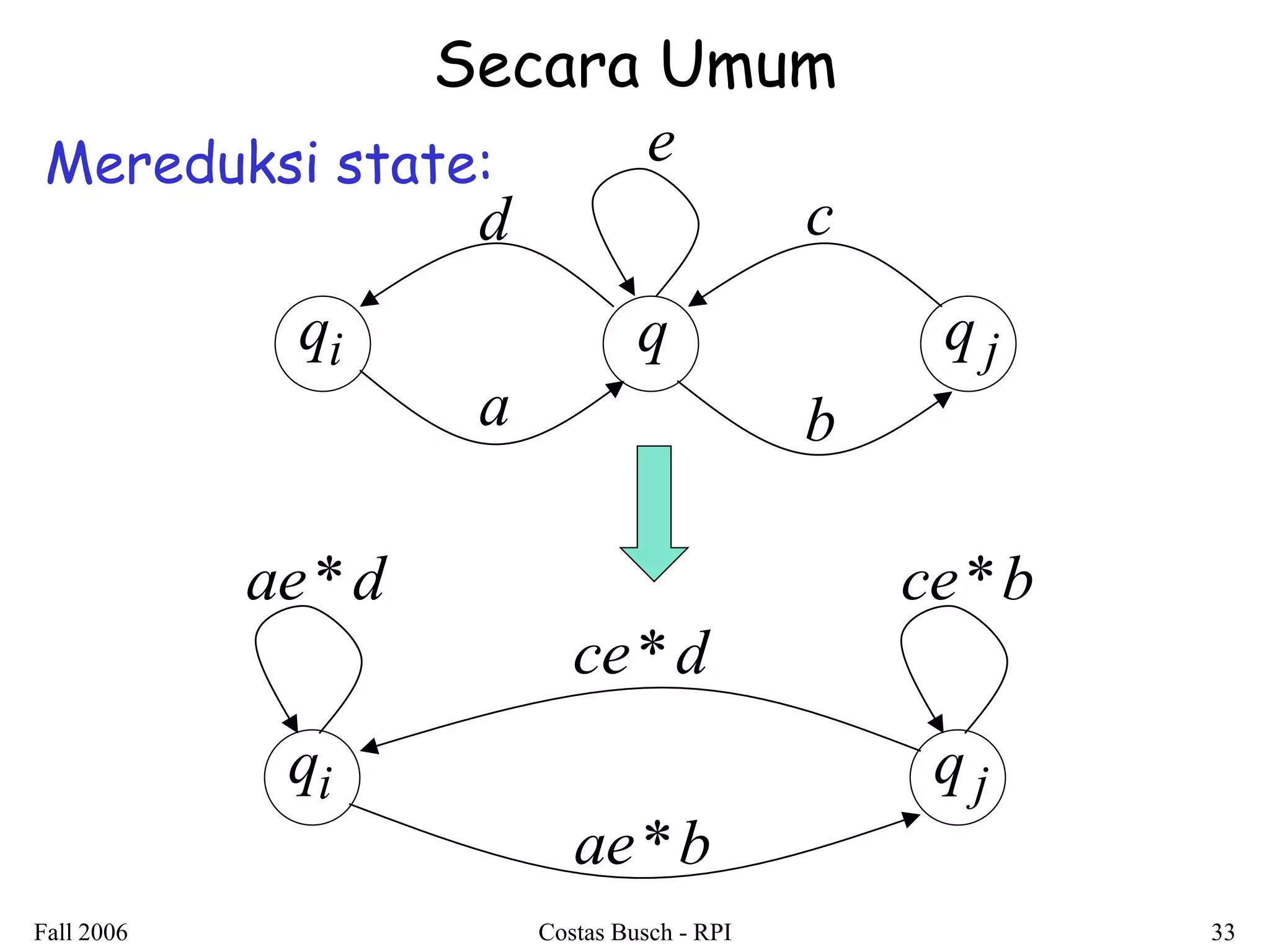
Dokumen ini membahas tentang regular expressions dan bahasa regular, menjelaskan definisi serta contoh-contoh penggunaannya. Terdapat juga penjelasan mengenai ekuivalensi antara regular expressions dan pembuktian bahwa bahasa yang dihasilkan adalah regular languages. Selain itu, dokumen ini mencakup teknik-teknik untuk mengonversi regular expressions menjadi non-deterministic finite automata (NFA).

1. ILMU KOMPUTASI
STMIK AMIKOM Purwokerto
Teknik Informatika
Fall 2006
Costas Busch - RPI
1

2. Fall 2006
Costas Busch - RPI
2
Regular Expressions

3. Fall 2006 Costas Busch - RPI 3
Regular Expressions
Regular expressions (RE)
Menjelaskan tentang bahasa regular (regular
languages)
Contoh:
Menjelaskan language
(a  bc)*
a,bc*  ,a,bc,aa,abc,bca,...

4. Fall 2006 Costas Busch - RPI 4
Recursive Definition
, , 
 1
1
1 2
1 2
*
r
r
r r
r r


Regular expressions
Primitif Regular expressions:
Untuk regular expressions r 1 and r2

5. Fall 2006 Costas Busch - RPI 5
Contoh :
Regular expression: a  bc*(c )
Bukan Regular expression: a  b 

6. Fall 2006 Costas Busch - RPI 6
Bahasa dari Regular Expressions
: bahasa dari regular expression
Contoh:
Lr r
L(a  bc)*  ,a,bc,aa,abc,bca,...

7. Fall 2006
Costas Busch - RPI
7
Defenisi :
Untuk primitif regular expressions:
  aaLLL    

8. Fall 2006 Costas Busch - RPI 8
Defenisi (cont’d)
Untuk Regular expressions dan
r1 r2
Lr1  r2   Lr1Lr2 
Lr1  r2   Lr1 Lr2 
Lr1*  Lr1*
Lr1  Lr1

9. Fall 2006 Costas Busch - RPI 9
Contoh :
Regular expression:  a  b a*
La  ba*  La  b La*
 La  b La*
 LaLb La*
 ab a*
 a,b,a,aa,aaa,...
 a,aa,aaa,...,b,ba,baa,...

10. Fall 2006 Costas Busch - RPI 10
Contoh :
Regular expression
r  a  b*a  bb
Lr  a,bb,aa,abb,ba,bbb,...

11. Fall 2006 Costas Busch - RPI 11
Contoh :
Regular expression r  aa*bb*b
  { : , 0} 2 2 L r  a b b n m  n m

12. Fall 2006 Costas Busch - RPI 12
Contoh :
Regular expression r  (0 1)*00 (0 1)*
L(r) = { semua strings berisi substring 00 }

13. Fall 2006 Costas Busch - RPI 13
Contoh :
Regular expression r  (1 01)*(0  )
L(r) = { semua strings tanpa substring 00 }

14. Fall 2006 Costas Busch - RPI 14
Ekuivalensi Regular Expressions
Defenisi:
Regular expressions dan
akan ekuivalen jika
r1 r2
L(r1)  L(r2)

15. Fall 2006 Costas Busch - RPI 15
Contoh :
L = { semua strings tanpa substring 00 }
r1  (1 01)*(0  )
r2  (1*011*)*(0 ) 1*(0 )
L(r1)  L(r2)  L
r1 dan r2
adalah regular
expressions ekuivalen

16. Fall 2006
Costas Busch - RPI
16
Regular Expressions dan Regular Languages

17. Fall 2006
Costas Busch - RPI
17
Teorema
Languages
Dibangkitkan dgn
Regular Expressions
Regular
Languages


18. Fall 2006 Costas Busch - RPI 18
Languages
Dibangkitkan dgn
Regular Expressions
Regular
Languages 
Languages
Dibangkitkan dgn
Regular Expressions
Regular
Languages 
Bukti:

19. Fall 2006 Costas Busch - RPI 19
Bukti - Part 1
r
L(r)
Untuk regular expression
Bahasa adalah regular
Languages
Dibangkitkan dgn
Regular Expressions
Regular
Languages 
Pembuktian dgn induksi pada ukuran r

20. Fall 2006 Costas Busch - RPI 20
Basis Induksi
Primitif Regular Expressions: , , 
NFAs yg sesuai :
L(M1)   L()
L(M2) {}  L( )
L(M3) {a}  L(a)
Regular
languages
a

21. Fall 2006 Costas Busch - RPI 21
Hypothesis Induktif
Misalkan :
Bahwa untuk regular expressions and ,
dan adalah regular languages
r1 r2
L(r1) L(r2)

22. Fall 2006 Costas Busch - RPI 22
Langkah Induktif
Kita akan buktikan :
 
 
 
 1
1
1 2
1 2
*
L r
L r
L r r
L r r


Adalah regular
Languages

23. Fall 2006
Costas Busch - RPI
23
Berdasarkan defenisi regular expressions:
   111121212121** rLrLrLrLrLrLrrLrLrLrrL    

24. Fall 2006 Costas Busch - RPI 24
L(r1) L(r2)
Dengan hipotesis induktif diketahui:
dan adalah regular languages
Regular languages tertutup untuk operasi:
   
   
  1*
1 2
1 2
L r
L r L r
Union L r  L r
Concatenation
Star
Diketahui juga :

25. Fall 2006 Costas Busch - RPI 25
Maka :
     
     
 1 *   1*
1 2 1 2
1 2 1 2
L r L r
L r r L r L r
L r r L r L r

 
  
Adalah regular
languages
(( )) ( ) 1 1 L r L r Hal yg biasa dr regular language
(dgn induksi hypothesis)
End of Proof-Part 1

26. Fall 2006 Costas Busch - RPI 26
Gunakan regular closure operasi ini,
Dpt di buat rekursif NFA yg diterima M
L(M) L(r )
Contoh: 1 2 r r r
( ) ( ) 1 1 L M L r
( ) ( ) 2 2 L M L r
L(M) L(r )



27. Fall 2006 Costas Busch - RPI 27
Untuk regular language dimana
regular expression dengan
Proof - Part 2
Languages
Dibangkitkan dgn
Regular Expressions
Regular
Languages 
L
r L(r)  L
Dapat dibuat NFA ekuivalensi dari bahasa
untuk regular expression nya
L

28. Fall 2006 Costas Busch - RPI 28
Karena adalah regular, ada NFA dari
yg menerima nya :
L M
L(M)  L
Dengan satu state akhir (1 accepting state)

29. Fall 2006 Costas Busch - RPI 29
Diagram transisi yg ekuivalen
di mana fungsi transisi adalah ekspresi reguler
M
Contoh:
a
a,b
c
M
a
a  b
c
Diagram Transisi yg sesuai
Secara umum

30. Fall 2006 Costas Busch - RPI 30
Contoh lain:
a  b
a
b
b
q0 q1 q2
a,b
a
b
b
q0 q1 q2
b
Fungsi transisi b
adalah regular
expressions

31. Fall 2006 Costas Busch - RPI 31
State hsl reduksi:
a  b
a
b
b
q0 q1 q2
b
q0 q2
bb*a b
bb*(a  b)
Fungsi transisi
adlh regular
expressions

32. Fall 2006 Costas Busch - RPI 32
Hasil Regular Expression:
q0 q2
bb*a b
bb*(a  b)
r  (bb*a)*bb*(a  b)b*
L(r)  L(M)  L

33. Fall 2006 Costas Busch - RPI 33
Secara Umum
Mereduksi state:
qi q q j
a b
d c
e
qi q j
ae*d ce*b
ce*d
ae*b

34. Fall 2006 Costas Busch - RPI 34
q0 q f
r1
r2
r3
r4
r  r1*r2(r4  r3r1*r2)*
L(r)  L(M)  L
Hasil regular expression nya :
Dgn mengulangi proses sampai dua state
Yg tersisa, diagram transisi hsl adlh:
Diagram awal Diagram hasil
End of Proof-Part 2

35. Fall 2006
Costas Busch - RPI
35
Representasi Standar untuk Regular Languages
Regular Languages
DFAs
NFAs
Regular
Expressions