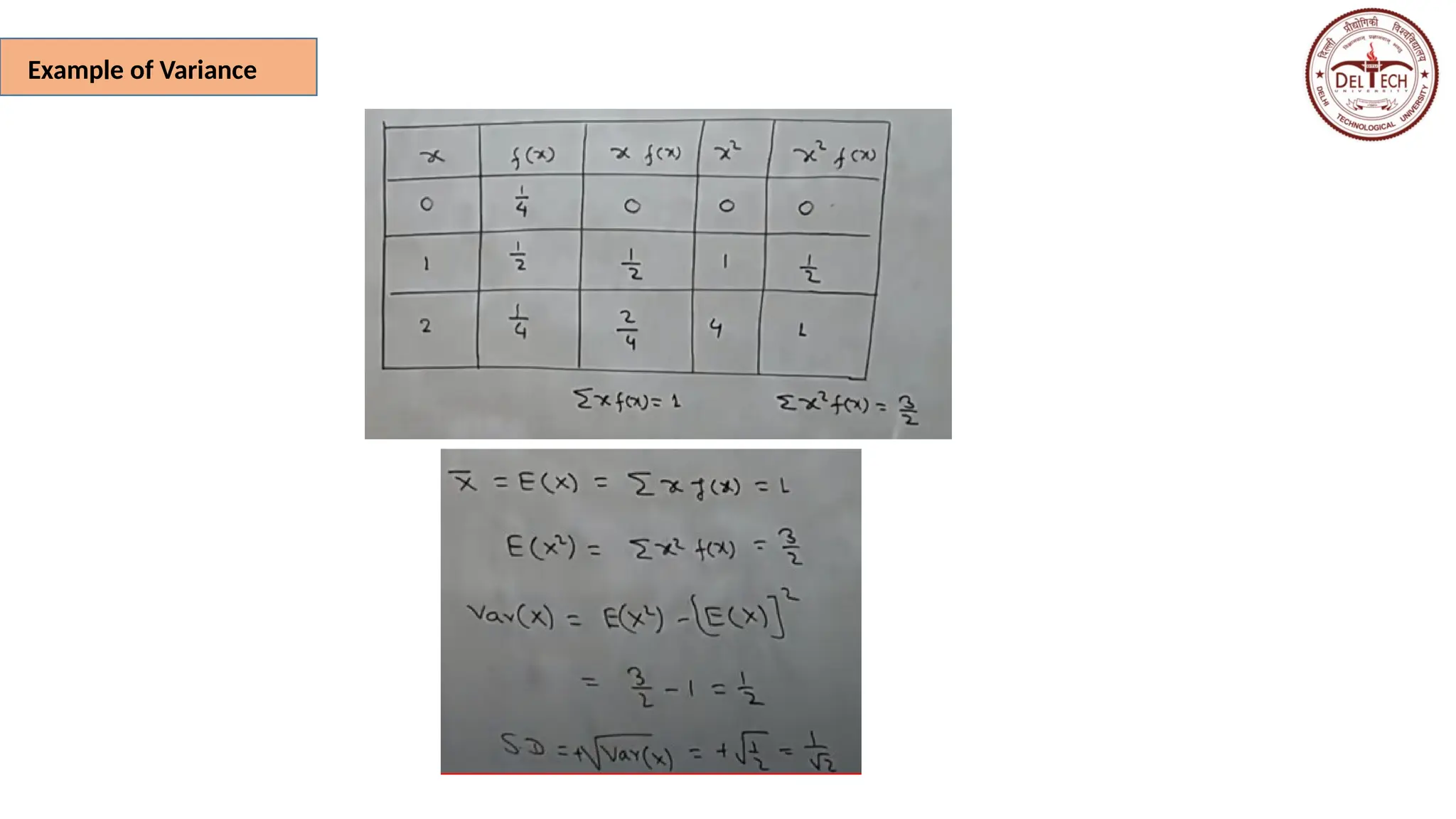
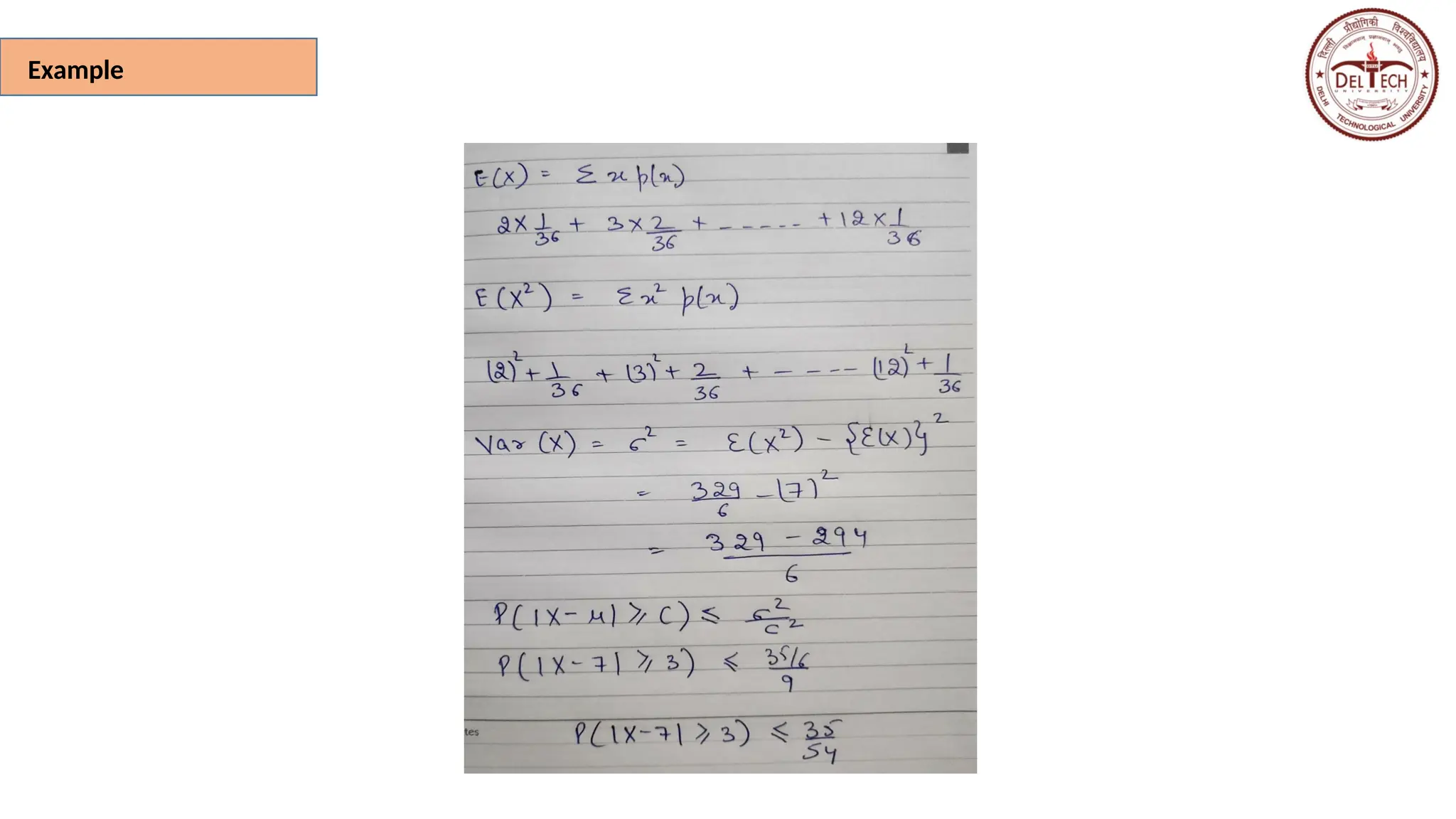The document covers the expectation and variance of random variables (RVs), detailing both discrete and continuous cases, as well as conditional expectations and covariance. It includes examples of calculating joint and marginal distributions and applying Chebyshev's inequality to assess probabilities related to RVs. Various calculations involving expectations and distributions from coin toss outcomes are also illustrated.

1. Course Syllabus

2. Chapter 3
OPERATIONS ON ONE RANDOM
VARIABLES

3. Expectation/Mean of RV
• Discrete Case: If X is a discrete random variable which can take the value x1, x2, x3……..xn with
respective probabilities p1, p2,………pn having
then the expectation of X, denoted by E(x) is defined as E(x)=p1x1 + p2x2+……..+pnxn =
• The expectation of discrete random variable X with PMF p(x) is defined as

4. Example in Discrete case

5. Expectation of RV
• Continuous Case: The expectation of continuous random variable X with PDF f(x) is defined as

6. Example in Continuous case

7. Expected value of function of RV
• Consider a random variable X with PDF or PMF f(x), If g(x) is a function of random variable X, then
E[g(x)] is defined as

8. Example

9. Variance of a RV
• The variance is mean squared difference between each data point and the centre of the distribution
measured by the mean.

10. Example of Variance

11. Conditional Expectation
DISCRETE CASE:
The conditional expectation or mean value of a function g(X, Y) given that Y=yi is defined by:

12. Conditional Expectation
CONTINUOUS CASE:
The conditional expectation or mean value of a function g(X, Y) given that Y=yi is defined by:

13. Example 1
Three coins are tossed. Let X denote the number of heads on the first two and Y denote the number of
heads on the last two. Find:
1. The joint distribution of X and Y.
2. Marginal distribution of X and Y.
3. E(X) and E(Y)
HHH HHT HTH THH HTT THT TTH TTT
X 2 2 1 1 1 1 0 0
Y 2 1 1 2 0 1 1 0

14. Example 1
HHH HHT HTH THH HTT THT TTH TTT
X 2 2 1 1 1 1 0 0
Y 2 1 1 2 0 1 1 0
X | Y 0 1 2 f(x) (Marginal)
0 1/8 1/8 0 1/4
JOINT DISTRIBUTION
1 1/8 2/8 1/8 1/2
2 0 1/8 1/8 1/4
f(y) 1/4 1/2 1/4 1

15. Example 1
X | Y 0 1 2 f(x) (Marginal)
0 1/8 1/8 0 1/4
1 1/8 2/8 1/8 1/2
2 0 1/8 1/8 1/4
f(y) 1/4 1/2 1/4 1

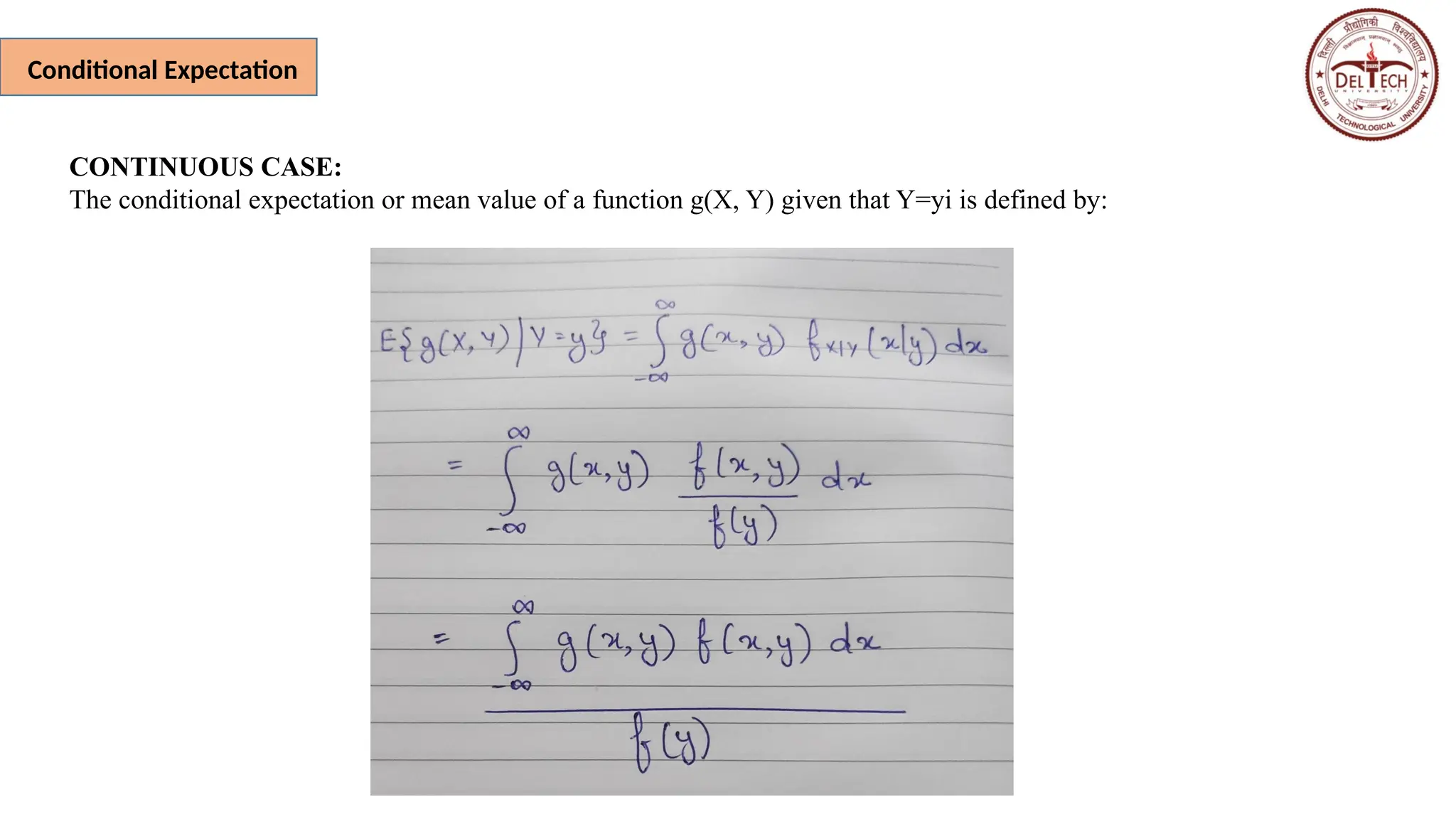
16. Example 2
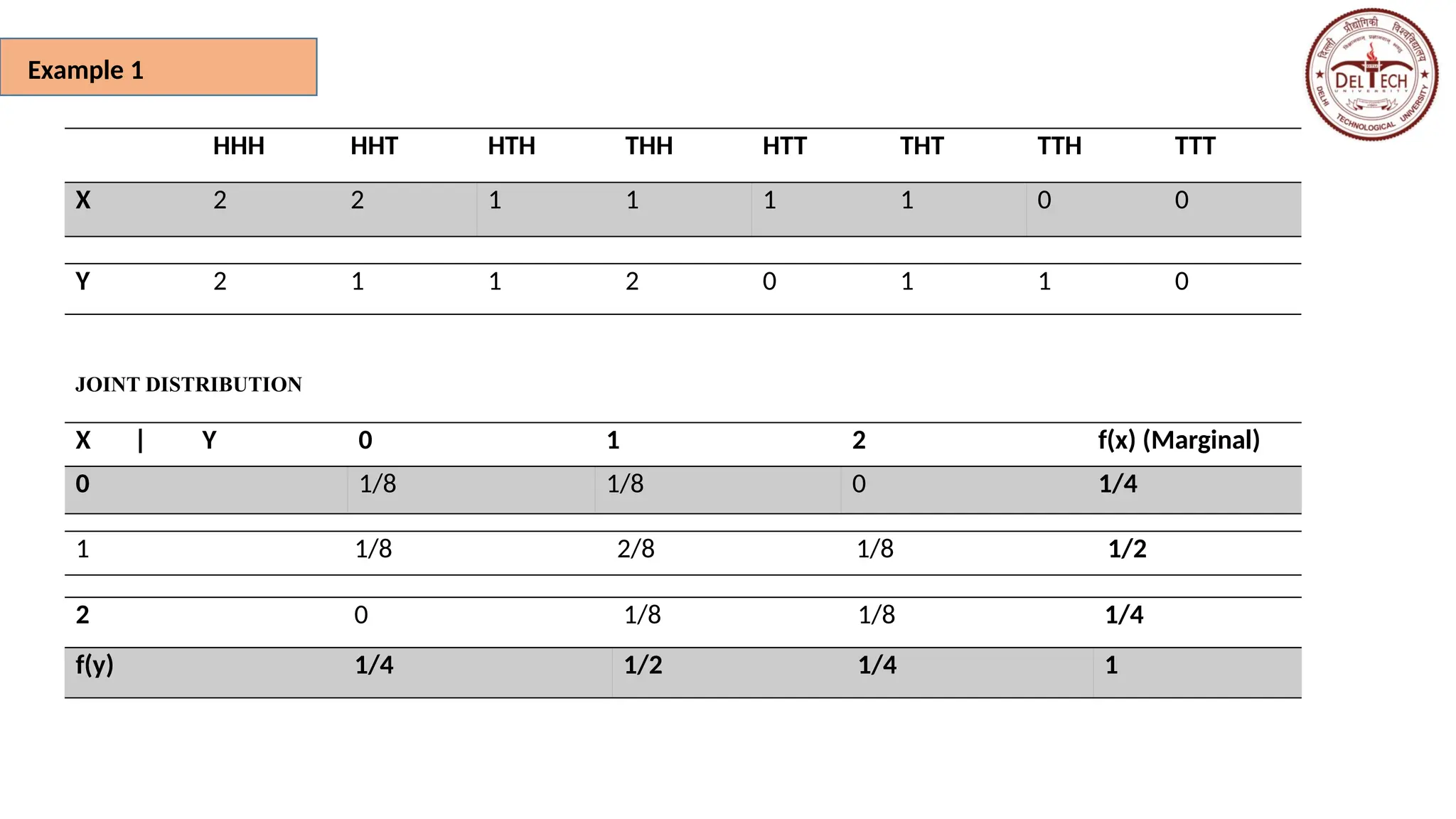
X | Y 0 1 2 f(x) (Marginal)
0 1/8 1/8 0 1/4
1 1/8 2/8 1/8 1/2
2 0 1/8 1/8 1/4
f(y) 1/4 1/2 1/4 1
Find E[ Y | X=1]

17. Example 2
Find E[ Y | X=1]

18. Covariance
Let X and Y be any two random variables and let E(X)=u1 and E(Y)=u2.
Consider the mathematical expectation
The number is known as covariance of X and Y and it is denoted by Cov (X, Y)

19. Chebyshev’s Inequality
Let X is a random variable with mean (μ) and variance (σ2
), then for any positive number k, we have
or

20. Example
Two unbiased dice are thrown. If X is the sum of the numbers showing up. Prove that P(|X-7|>=3)<=35/54.
Compare this with the actual probability.

21. Example

22. Example
Actual Probability=1/3=0.333
Chebyshev’s
inequality=35/54=0.648
0.333<=0.648