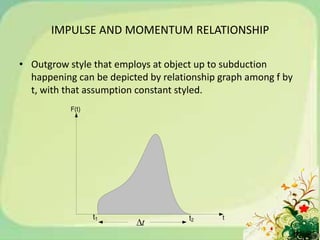
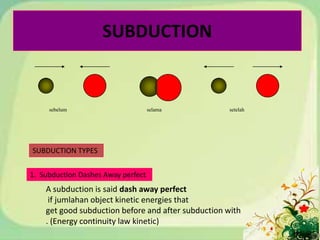
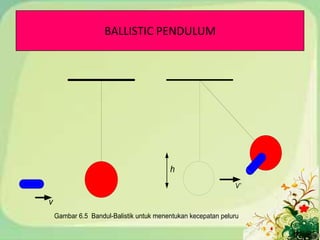
Rahmawati Yusri applies for a position. She provides her name, student ID number, and materials on various physics topics in 3 dimensions, including: 1) Impulse and momentum relationships for objects with constant force over time. 2) Types of collisions, including perfectly elastic, inelastic, and completely inelastic collisions. 3) Using a ballistic pendulum to determine the velocity of a bullet. 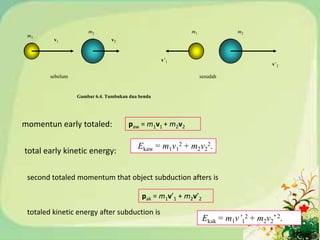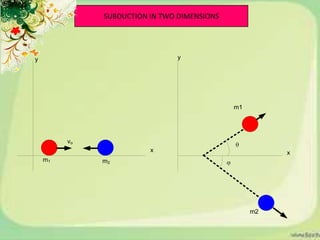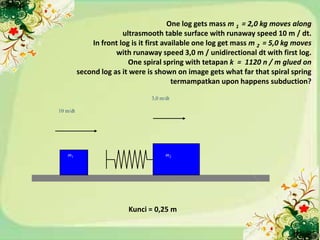4) Momentum in two-dimensional collisions and solving example problems. 5) Rocket thruster energy and deriving an equation relating velocity to fuel mass over time for a rocket.

1. Name : Rahmawati Yusri
NIM : RSA1C311001

2. APLICATION
SUBDUCTION
THE MATERIAL PENDULUM
SUBDUCTION TWO
DIMENSIONS
ROCKET

3. IMPULSE AND MOMENTUM RELATIONSHIP
• Outgrow style that employs at object up to subduction
happening can be depicted by relationship graph among f by
t, with that assumption constant styled.
F(t)
t1 t2 t
t

4. • One particle gets mass m one that moving with speed v having linear
.
momentum p one that constitute multiple among that particle speed
with its mass
v
m p = mv.
Legally Newton II. resultant inspires that is conected with one
straight proportionate object with velocity
F = ma.
d ( mv ) dp
F
dt dt
dp=Fdt
If each diintegralkan therefore acquired:

5. p2 t2
p1 p2 dp F .dt
p1 t1
Linear Momentum continuity
If resultant external style that employs at system equal to zero, therefore
momentum vector total system makes a abode constant
dp
0
dt
For particle system
p1 p2 ........ pn p

6. SEVERALLY MOMENTUM PRINCIPLE PURPOSE
• Two logs A and b one gets mA's masses and mB, one that
linked by one spiral spring and lie upon horizontal table
without friction. Our spiral spring strungs strikingly both of log
to sideways as on image.
y
A
B
x
O

7. The one log gets positive momentum( A moves in aim + x) and bemomentum negative's
the other log (B moving deep tenor –x) from hokum our conservation of momentum
gets:
Early momentum = final momentum
0 mBvB m Av A
mBvB m Av A
Or mB
vA vB
mA

8. SUBDUCTION
sebelum selama setelah
SUBDUCTION TYPES
1. Subduction Dashes Away perfect
A subduction is said dash away perfect
if jumlahan object kinetic energies that
get good subduction before and after subduction with
. (Energy continuity law kinetic)

9. m2 m1 m2
m1
v1 v2
v’1
v’2
sebelum sesudah
Gambar 6.4. Tumbukan dua benda
momentun early totaled: paw = m1v1 + m2v2
Ekaw = m1v12 + m2v22.
total early kinetic energy:
second totaled momentum that object subduction afters is
pak = m1v’1 + m2v’2
totaled kinetic energy after subduction is
Ekak = m1v’12 + m2v2’ 2.

10. paw = pak m1v1 + m2v2 = m1v’1 + m2v’2 m1(v1 − v’1) = m2(v’2 − v2),
Ekaw = Ekak m1v12 + m2v22 = m1v’12 + m2v2’ 2 or
m1v12 − m1v’12 = m2v2’ 2 − m2v22 or
m1 (v1 − v’1)( v1 + v’1) = m2(v’2 − v2) (v’2 +
v2)
Of two box deep equations tingle to be gotten
v ' 2 v '1
v1 + v’1 = v’2 + v2 ot 1
v2 v1
v ' 2 v '1
In common compare e
v2 v1

11. 2. Subduction Dashes Away to play favorites
After subduction there is a portion changed mechanical energy as heat energy, sound
or the other energy. So after subduction available exempt energy. Mechanical energy
continuity law inoperative. On this subduction is distinguished its elasticity price is 0
<e<1
3. Subduction Does Not Dash Away absolutely
After second object subduction clings to become one and moving with afterses same
speed subduction both of menyatu's object. E=0's price

12. BALLISTIC PENDULUM
h
V’
v
Gambar 6.5 Bandul-Balistik untuk menentukan kecepatan peluru

13. If shot mass is m and pendulum mass be m, with momentum
continuity is gotten
mv (m M )v '
system energy on the turn as shot potential energy with pendulum until up
until shot oscillation top pendulum
1 2
(m M )v ' (m M ) gh or v' 2 gh
2
If equation in yellow box at merged acquired:
m M
v 2 gh
m

14. SUBDUCTION IN TWO DIMENSIONS
y y
m1
vo
x x
m1 m2
m2

15. kelesterian is momentum for each one aim
Wicked aim x: m m vo m 1 v 1 cos . m 2 v 2 cos .
Wicked aim y: 0 m 1 v1 sin m 2 v 2 sin
If subduction gets elastic character 1 2 1 2 1 2
m1v o m 1 v1 m2v2
2 2 2
But if inelastis's subduction 1 2 1 2 1 2
mv
1 o
mv1 1
m 2v2 Ei
2 2 2
billiard's ball with speed 30 m / s menumbuk serves a ball biliard II. one holds tongue
and get masses with. After subduction, moving i. ball deviates 30 o of aim originally.
Look for speed each ball and power aim serves a ball II.. (elastic reputed subduction)

16. One log gets mass m 1 = 2,0 kg moves along
ultrasmooth table surface with runaway speed 10 m / dt.
In front log is it first available one log get mass m 2 = 5,0 kg moves
with runaway speed 3,0 m / unidirectional dt with first log.
One spiral spring with tetapan k = 1120 n / m glued on
second log as it were is shown on image gets what far that spiral spring
termampatkan upon happens subduction?
3,0 m/dt
10 m/dt
m1 m2
Kunci = 0,25 m

17. Rocket Thruster energy
• Rockets early momentum p 1 =mv
• Upon + dt rocket speed increases v + dv. For example
m mass that gushes about satuan time. Rocket mass
stays behind m? dt, detached fueled mass? dt.
• If vr relative rocket speed to fuel that gushes.
• v ’ =v vr
• Eventual momentum is (m? dt) (v + dv)
• Fueled momentum that tersembu is v ’ dt

18. Therefore prevailing: -
mgdt=((m- dt)(v+dv)+v’ dt)-mv
If m huge therefore m dtdv can be ignored
So: mdv=vr dt-mgdt
dm=- dt, so is gotten:
dm
dv vr gdt
m
By integrates is gotten:
v=-vrlnm-gt+C
If modan vo mass and kec while t=0 therefore
vo=-vrlnmo+C
Dan v=vo-gt+vrln(mo/m)

19. Neutrino case
• If two object fly to be diqoined by speeds v 1
and v 2 therefore kinetic energy it also
separate:
• Q=K 1 + K 2 =1 / 2 m 1 2 +1 / 2 m 2 2
• Second particle momentum has to equal
zero so:
• m 1 v 1 = -m 2 v 2
• If both of dikuadratkan's equation and at
divides two therefore acquired:

20. 1/2m12v12=1/2m22v22
m1K1=m2K2
If this equation compounded by
equation upon acquired:
m2 m1
K1 m1 m 2
Q K2 m1 m 2
Q

21. I THINK THAT’S ALL MY PRESENTATION…
FORGIVE ME FOR MY MISTAKE..
AND SEE YOU IN THE NEXT CONDITION..
ASSALAMU’ALAYKUM WA RAHMATULLAH
WA BARAKATUH…