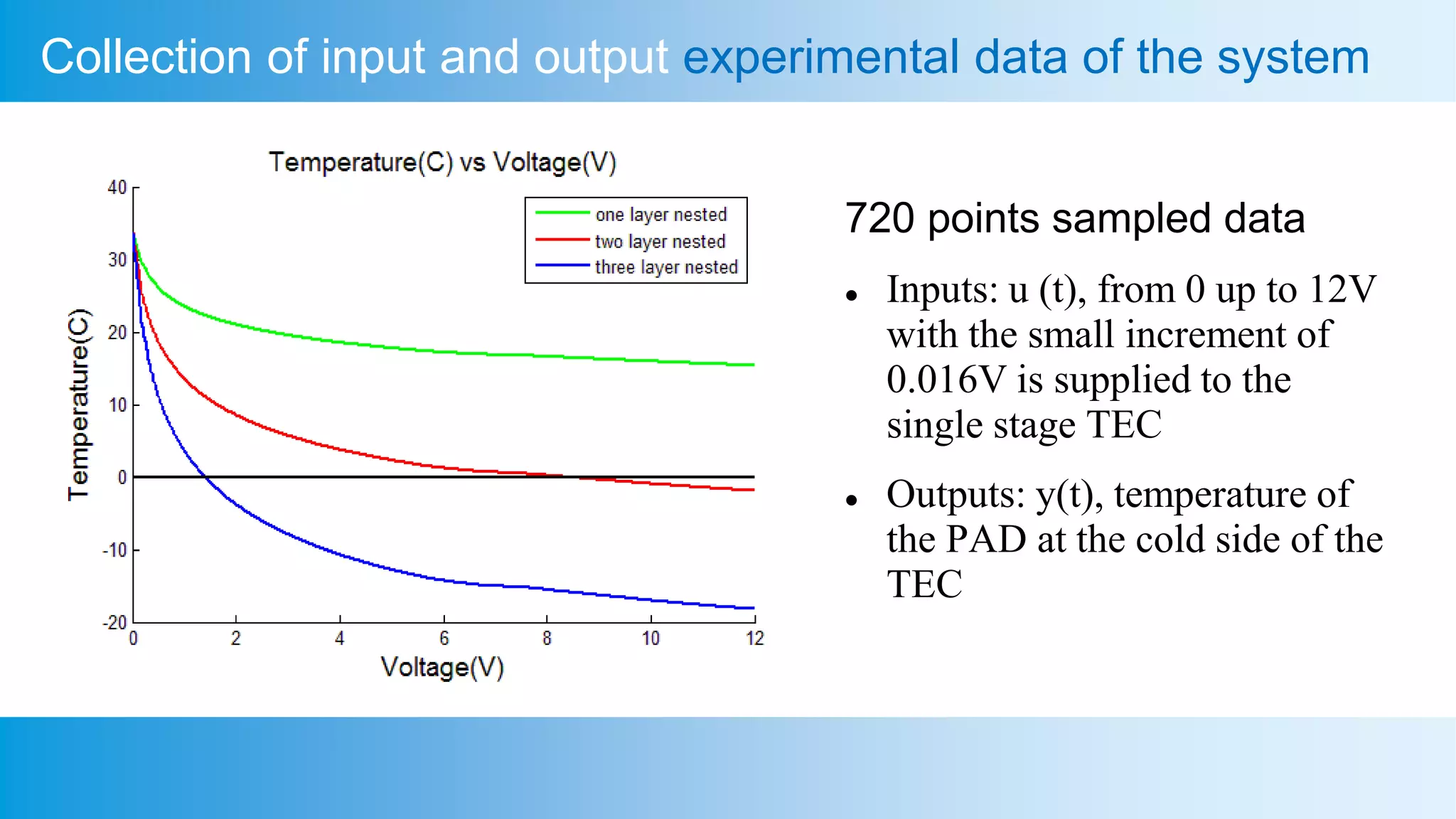
This document presents an analysis of a semiconductor-based micro refrigerator designed for quantum computing devices, focusing on optimization through a brain storm optimization algorithm. It discusses the development of a mathematical model for a thermoelectric cooler, including its application for cooling a photon avalanche diode, and details the processes involved in parametric system identification. The findings include a quick convergence of the mean square error as the objective function, demonstrating the effectiveness of the optimization method employed.

1. Analysis of Semiconductor based Micro
Refrigerator for Quantum Devices
Tong Xu1, Siqing Ma2, Jun Steed Huang3
1,3 Institute of Prospective Autonomous Driving, Nanjing 210000, China
2 Southern University of Science and Technology, Shenzhen 518000, China
August 28-30, 2019, Wireless Valley, Nanjing, China
2019 IEEE International Symposium on Radio-Frequency Integration Technology

2. About the Authors
Tong Xu, Patent Engineer
Siqing Ma, Project Engineer
Jun Steed Huang, Principal Engineer

3. Outline
I. Introduction Cooling
II. Brain Storm Optimization
III. Parametric System Identification
IV. Simulation Results

4. In order to provide the design guidance for a multiple stage refrigerator for
hosting a quantum computing device targeting for unmanned transportation
platform. We provides a modeling analysis based on a preliminary single stage
test data, by using Brain Storm Optimization algorithm.
Introduction Cooling

5. Cooling device
Cooling device——Thermo Electric Cooler (TEC)
TEC use the Peltier effect through p-type and n-type semiconductor
elements. TEC are widely used in cooling, maintaining and
stabilizing the temperature of the devices like Photon Avalanche
Diode, etc.
A single TEC

6. PAD is a temperature sensitive
optoelectronic device, where even a
slight variation in temperature can
cause unstable performance in
quantum efficiency, responsibility
and dark counts.
Cooling object——Photon Avalanche Diode (PAD)
Cooling object

7. Three-layer nested cooling system
A TEC heat sink unit (One stage)
We use a three-layer nested
multi-stage micro-refrigeration
system to improve the
traditional coolant based multi-
stage refrigeration system,
which consist of PAD, TEC and
a custom mounting design of
heat sink and the cooling heat
exchanger components is
specifically designed to fulfill
the purpose.

8. Modeling and optimization
 In this study, the mathematical model of a TEC together with its mounting
design with PAD is obtained using the Brain Storm Optimization (BSO)
algorithm in MATLAB.
 A highly nonlinear characteristic of TEC has made the normal equations
derivation becoming more complex.
 Use Brain Storm Optimization (BSO) to simulate the mathematical model of
a TEC together with its mounting design with PAD

9. Brain Storm Optimization
Brain Storm Optimization (BSO) is an
optimization algorithm that was inspired by
human being creative problem solving process.
This new algorithm combines the advantages
of swarm intelligence and data mining,
choosing better solution based on data analysis.
Each solution in this swarm intelligence
optimization algorithm is regarded as a data
point, and the optimal solution is found by
clustering data points.

10. BSO details
The solution update to their new solution by:
Xnew
d
= Xselected
d
+ ξ t × N μ, σ
where Xselected
d
is the d-th dimension of the individual selected to generate new
individual; Xnew
d
is the d-th dimension of the individual newly generated; N(μ,
σ) is the Gaussian random function with mean μ and variance σ; the ξ(t) is a
coefficient that weights the contribution of the Gaussian random value.
For the simplicity and for the purpose offline tuning, the ξ can be calculated as
ξ t = logsig(
0.5×T–t
𝑘
) × rand()
.
where logsig() is a logarithmic sigmoid transfer function, T is the maximum
number of iterations, and t is the current iteration number, k is for changing
logsig() function’s slope, and rand() is a random value within (0,1). The transfer
function formula logsig() is defined as follows:
logsig a =
1
1+exp(–𝑎)

11. Parametric System Identification
Parametric system identification is defined by the model structure and
parameters from a given data input and output to describe the real physical
system.
Parametric system identification is a practice of control and prediction of a
real world physical system. The determination of mathematical model using
BSO is realized by minimizing the mean square error prediction output to the
actual output of the system.
There are three steps in determining parameter system identification:
• Collection of input and output experimental data of the system
• Determination of the model structure
• Selection of the parameters mathematical model

12. Collection of input and output experimental data of the system
720 points sampled data
 Inputs: u (t), from 0 up to 12V
with the small increment of
0.016V is supplied to the
single stage TEC
 Outputs: y(t), temperature of
the PAD at the cold side of the
TEC

13. Determination of the model structure
BSO based parametric system identification of TEC for PAD application

14. Selection of the parameters mathematical model
The below equation is the model structure of auto regression with exogenous input
(ARX) was chosen to represent the model structure of the system:
𝑦 𝑡 =–
𝑖=1
𝑁
𝑎𝑖 × 𝑦 𝑡– 𝑖 +
𝑗=0
𝑁
𝑏𝑖 × 𝑢 𝑡– 𝑗
where,
ŷ (t) = The predicted output ;
ai = The denominator ;
bj = The numerator ;
N = The number of the denominator ;
M = The number of the numerator ;
u (t) = The input ;
y (t) = The actual output

15. Selection of the parameters mathematical model
Mean Square Error (MSE), proposed by Gauss,
which is the objective function for the BSO optimization process.
The result of the MSE should converge to zero:
e(t )=MSE=
1
N
t=1
N
y t – y t 2

16. Simulation Results
The mathematical model obtained
from the BSO simulation is：
𝑦 t =– 𝑎1y t– 1 – 𝑎2y t– 2 + 𝑏0u t + 𝑏1u t– 1
The parameters of the corresponding
parameter system for each layer are shown
in the below table:
layer parameters a1 a2 b0 b1
one layer -2.1364 1.1337 -3.0008 3.0015
two layer -1.7759 0.7788 0.1146 -0.1151
three layer -2.0682 1.0651 0.7484 -0.7440

17. Simulation table figure
The blue lines are the actual output
while the green lines are the BSO
predicted output.
By substituting the respective
parameters, we can get the Mean
Square Error at very small level.

18. Conclusion
--The BSO algorithm use random solutions to replace clustering
centers in solution set, which can help BSO to avoid achieving a
premature convergence of local optimal solution.
--Regression with exogenous input is found to be the second order
model structure of the system.
--Mean Square Error was used as the objective function of BSO, it
converged quickly.

19. ACKNOWLEDGMENT
Thanks go to:
Prof. Yuhui Shi, Prof. Shi Cheng (Sustech project)
Prof. Hongwei Shi, Mr. Hongbin Qian (Midea project)
and Ms. Jiamin Huang et al (Haylion project)
for discussions and supports!

20. Thank you !
Questions?
https://github.com/TongXu2
Autonomous is the way to go …