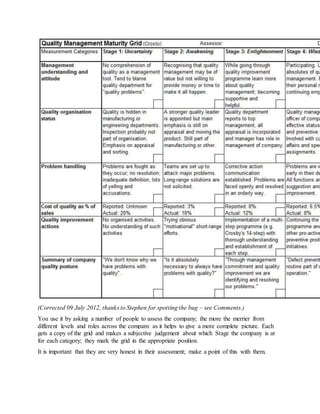
This document discusses quality management maturity grids and provides resources on quality management. It introduces Philip Crosby's Quality Management Maturity Grid, which is a 5x6 matrix that assesses an organization's quality management maturity across six categories. It can identify an organization's current stage of maturity and provide a roadmap for quality improvement. The document also lists several quality management tools, such as check sheets, control charts, Pareto charts, scatter plots, Ishikawa diagrams, and histograms. Additional related topics on quality management are provided.

1. Quality management maturity grid
In this file, you can ref useful information about quality management maturity grid such as
quality management maturity gridforms, tools for quality management maturity grid, quality
management maturity gridstrategies … If you need more assistant for quality management
maturity grid, please leave your comment at the end of file.
Other useful material for quality management maturity grid:
• qualitymanagement123.com/23-free-ebooks-for-quality-management
• qualitymanagement123.com/185-free-quality-management-forms
• qualitymanagement123.com/free-98-ISO-9001-templates-and-forms
• qualitymanagement123.com/top-84-quality-management-KPIs
• qualitymanagement123.com/top-18-quality-management-job-descriptions
• qualitymanagement123.com/86-quality-management-interview-questions-and-answers
I. Contents of quality management maturity grid
==================
Of all the quality ‘gurus’ I find the late Philip Crosby one of the most readable. In his
book ‘Quality is Free’ (Mentor 1980, ISBN 978-0451625854), which I can thoroughly
recommend, he advocates the use of a simple tool to show where you are in the quality
management spectrum; he calls it the Quality Management Maturity Grid.
The grid is a simple 5 x 6 matrix that shows different stages of maturity of the company’s quality
management against six different quality management categories (management understanding of
quality, problem handling, cost of quality, etc).
The lowest stage of maturity is called ‘Uncertainty’ – the organisation is inexperienced, quality
management is a low priority and reactive, etc – then as quality management matures it goes
through the stages of ‘Awakening’, ‘Enlightenment’, ‘Wisdom’, then the highest level,
‘Certainty’.
Each point – maturity versus category – on the grid has a brief description of how that
combination appears in the company; for instance, in the ‘Uncertainty’ stage, Problem Handling
looks like “Problems are fought as they occur; no resolution; inadequate definition; lots of
yelling and accusations.” If that sounds like your company then I’m sorry to hear it and you are
at the ‘Uncertainty’ stage for Problem Handling!
Here’s the grid (I know it’s difficult to read in some browsers as it’s shown below; you can either
make your browser window a lot wider or click on it a couple of times to see it more clearly):

2. (Corrected 09 July 2012, thanks to Stephen for spotting the bug – see Comments.)
You use it by asking a number of people to assess the company; the more the merrier from
different levels and roles across the company as it helps to give a more complete picture. Each
gets a copy of the grid and makes a subjective judgement about which Stage the company is at
for each category; they mark the grid in the appropriate position.
It is important that they are very honest in their assessment; make a point of this with them.

3. (By the way, you may find Cost of Quality a bit tricky to estimate if I don’t explain what it really
means; sorry about that, I’ll have to blog about it another time. In the meantime, have a look at
Jim Wells’ excellent description here.)
The total score is obtained by adding up the scores for each category; Stage 1 ‘Uncertainty’ gives
a score of 1, Stage 2 ‘Awakening’ = 2, Stage 3 = 3, etc. The minimum score is therefore 6 (all
categories are at ‘Uncertainty), and the maximum is 30 (all are at Certainty); I know of no
company that is at 30 so if you really are there please get in touch as I’d really like to meet you!
It is really interesting not only to see the scores for each category (as well as the total), and the
arithmetic mean across all the assessors, but also to see how individuals from different
departments or roles in the company mark each category; big variances in scores indicate that
people see the company as being very different in this area – why is that? Is the high score or the
low score more appropriate? What needs to be done about a low score from just one part of the
business? It can be a fascinating exercise.
The thing I particularly like about the Quality Management Maturity Grid is that it is (a) very
quick and easy to use, (b) insightful – it makes you think, and (c) – most important – it doesn’t
just show you where you are but, also, what your company would have to be like to get a higher
score; it therefore acts as your route-map for strategic quality and helps you plan your quality
improvement initiatives so that you move steadily towards the right in the grid.
==================
III. Quality management tools
1. Check sheet
The check sheet is a form (document) used to collect data
in real time at the location where the data is generated.
The data it captures can be quantitative or qualitative.
When the information is quantitative, the check sheet is
sometimes called a tally sheet.
The defining characteristic of a check sheet is that data
are recorded by making marks ("checks") on it. A typical
check sheet is divided into regions, and marks made in
different regions have different significance. Data are
read by observing the location and number of marks on
the sheet.
Check sheets typically employ a heading that answers the
Five Ws:
 Who filled out the check sheet
 What was collected (what each check represents,

4. an identifying batch or lot number)
 Where the collection took place (facility, room,
apparatus)
 When the collection took place (hour, shift, day
of the week)
 Why the data were collected
2. Control chart
Control charts, also known as Shewhart charts
(after Walter A. Shewhart) or process-behavior
charts, in statistical process control are tools used
to determine if a manufacturing or business
process is in a state of statistical control.
If analysis of the control chart indicates that the
process is currently under control (i.e., is stable,
with variation only coming from sources common
to the process), then no corrections or changes to
process control parameters are needed or desired.
In addition, data from the process can be used to
predict the future performance of the process. If
the chart indicates that the monitored process is
not in control, analysis of the chart can help
determine the sources of variation, as this will
result in degraded process performance.[1] A
process that is stable but operating outside of
desired (specification) limits (e.g., scrap rates
may be in statistical control but above desired
limits) needs to be improved through a deliberate
effort to understand the causes of current
performance and fundamentally improve the
process.
The control chart is one of the seven basic tools of
quality control.[3] Typically control charts are
used for time-series data, though they can be used
for data that have logical comparability (i.e. you
want to compare samples that were taken all at
the same time, or the performance of different
individuals), however the type of chart used to do
this requires consideration.

5. 3. Pareto chart
A Pareto chart, named after Vilfredo Pareto, is a type
of chart that contains both bars and a line graph, where
individual values are represented in descending order
by bars, and the cumulative total is represented by the
line.
The left vertical axis is the frequency of occurrence,
but it can alternatively represent cost or another
important unit of measure. The right vertical axis is
the cumulative percentage of the total number of
occurrences, total cost, or total of the particular unit of
measure. Because the reasons are in decreasing order,
the cumulative function is a concave function. To take
the example above, in order to lower the amount of
late arrivals by 78%, it is sufficient to solve the first
three issues.
The purpose of the Pareto chart is to highlight the
most important among a (typically large) set of
factors. In quality control, it often represents the most
common sources of defects, the highest occurring type
of defect, or the most frequent reasons for customer
complaints, and so on. Wilkinson (2006) devised an
algorithm for producing statistically based acceptance
limits (similar to confidence intervals) for each bar in
the Pareto chart.
4. Scatter plot Method

6. A scatter plot, scatterplot, or scattergraph is a type of
mathematical diagram using Cartesian coordinates to
display values for two variables for a set of data.
The data is displayed as a collection of points, each
having the value of one variable determining the position
on the horizontal axis and the value of the other variable
determining the position on the vertical axis.[2] This kind
of plot is also called a scatter chart, scattergram, scatter
diagram,[3] or scatter graph.
A scatter plot is used when a variable exists that is under
the control of the experimenter. If a parameter exists that
is systematically incremented and/or decremented by the
other, it is called the control parameter or independent
variable and is customarily plotted along the horizontal
axis. The measured or dependent variable is customarily
plotted along the vertical axis. If no dependent variable
exists, either type of variable can be plotted on either axis
and a scatter plot will illustrate only the degree of
correlation (not causation) between two variables.
A scatter plot can suggest various kinds of correlations
between variables with a certain confidence interval. For
example, weight and height, weight would be on x axis
and height would be on the y axis. Correlations may be
positive (rising), negative (falling), or null (uncorrelated).
If the pattern of dots slopes from lower left to upper right,
it suggests a positive correlation between the variables
being studied. If the pattern of dots slopes from upper left
to lower right, it suggests a negative correlation. A line of
best fit (alternatively called 'trendline') can be drawn in
order to study the correlation between the variables. An
equation for the correlation between the variables can be
determined by established best-fit procedures. For a linear
correlation, the best-fit procedure is known as linear
regression and is guaranteed to generate a correct solution
in a finite time. No universal best-fit procedure is
guaranteed to generate a correct solution for arbitrary
relationships. A scatter plot is also very useful when we
wish to see how two comparable data sets agree with each
other. In this case, an identity line, i.e., a y=x line, or an
1:1 line, is often drawn as a reference. The more the two
data sets agree, the more the scatters tend to concentrate in
the vicinity of the identity line; if the two data sets are
numerically identical, the scatters fall on the identity line

7. exactly.
5.Ishikawa diagram
Ishikawa diagrams (also called fishbone diagrams,
herringbone diagrams, cause-and-effect diagrams, or
Fishikawa) are causal diagrams created by Kaoru
Ishikawa (1968) that show the causes of a specific
event.[1][2] Common uses of the Ishikawa diagram are
product design and quality defect prevention, to identify
potential factors causing an overall effect. Each cause or
reason for imperfection is a source of variation. Causes
are usually grouped into major categories to identify these
sources of variation. The categories typically include
 People: Anyone involved with the process
 Methods: How the process is performed and the
specific requirements for doing it, such as policies,
procedures, rules, regulations and laws
 Machines: Any equipment, computers, tools, etc.
required to accomplish the job
 Materials: Raw materials, parts, pens, paper, etc.
used to produce the final product
 Measurements: Data generated from the process
that are used to evaluate its quality
 Environment: The conditions, such as location,
time, temperature, and culture in which the process
operates
6. Histogram method

8. A histogram is a graphical representation of the
distribution of data. It is an estimate of the probability
distribution of a continuous variable (quantitative
variable) and was first introduced by Karl Pearson.[1] To
construct a histogram, the first step is to "bin" the range of
values -- that is, divide the entire range of values into a
series of small intervals -- and then count how many
values fall into each interval. A rectangle is drawn with
height proportional to the count and width equal to the bin
size, so that rectangles abut each other. A histogram may
also be normalized displaying relative frequencies. It then
shows the proportion of cases that fall into each of several
categories, with the sum of the heights equaling 1. The
bins are usually specified as consecutive, non-overlapping
intervals of a variable. The bins (intervals) must be
adjacent, and usually equal size.[2] The rectangles of a
histogram are drawn so that they touch each other to
indicate that the original variable is continuous.[3]
III. Other topics related to Quality management maturity grid (pdf download)
quality management systems
quality management courses
quality management tools
iso 9001 quality management system
quality management process
quality management system example
quality system management
quality management techniques
quality management standards
quality management policy
quality management strategy
quality management books