The University of Western Australia, profile picture
Uploaded byThe University of Western Australia
707 views

David Lumley - 4D uncertainty - Nov 11, 2015

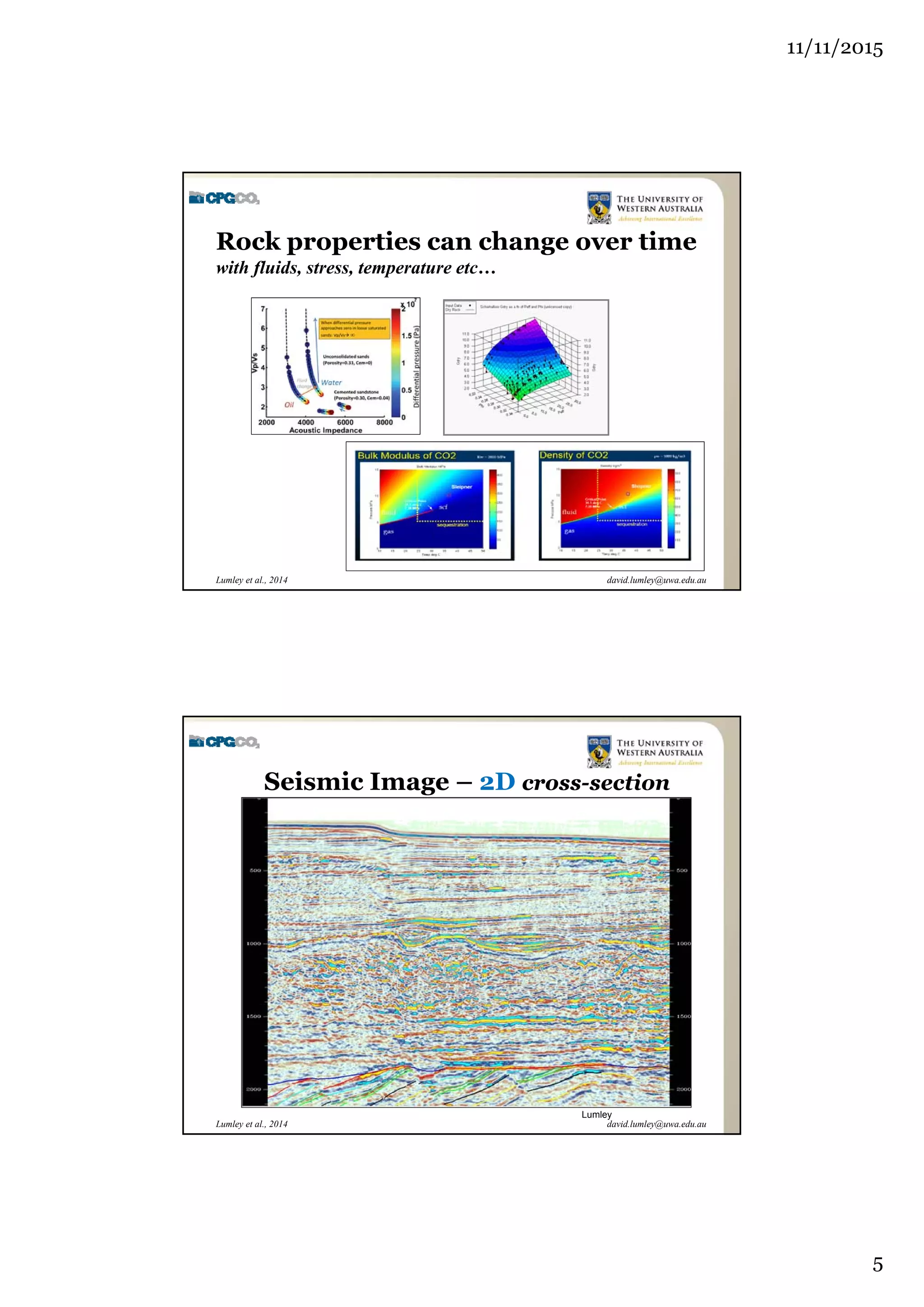
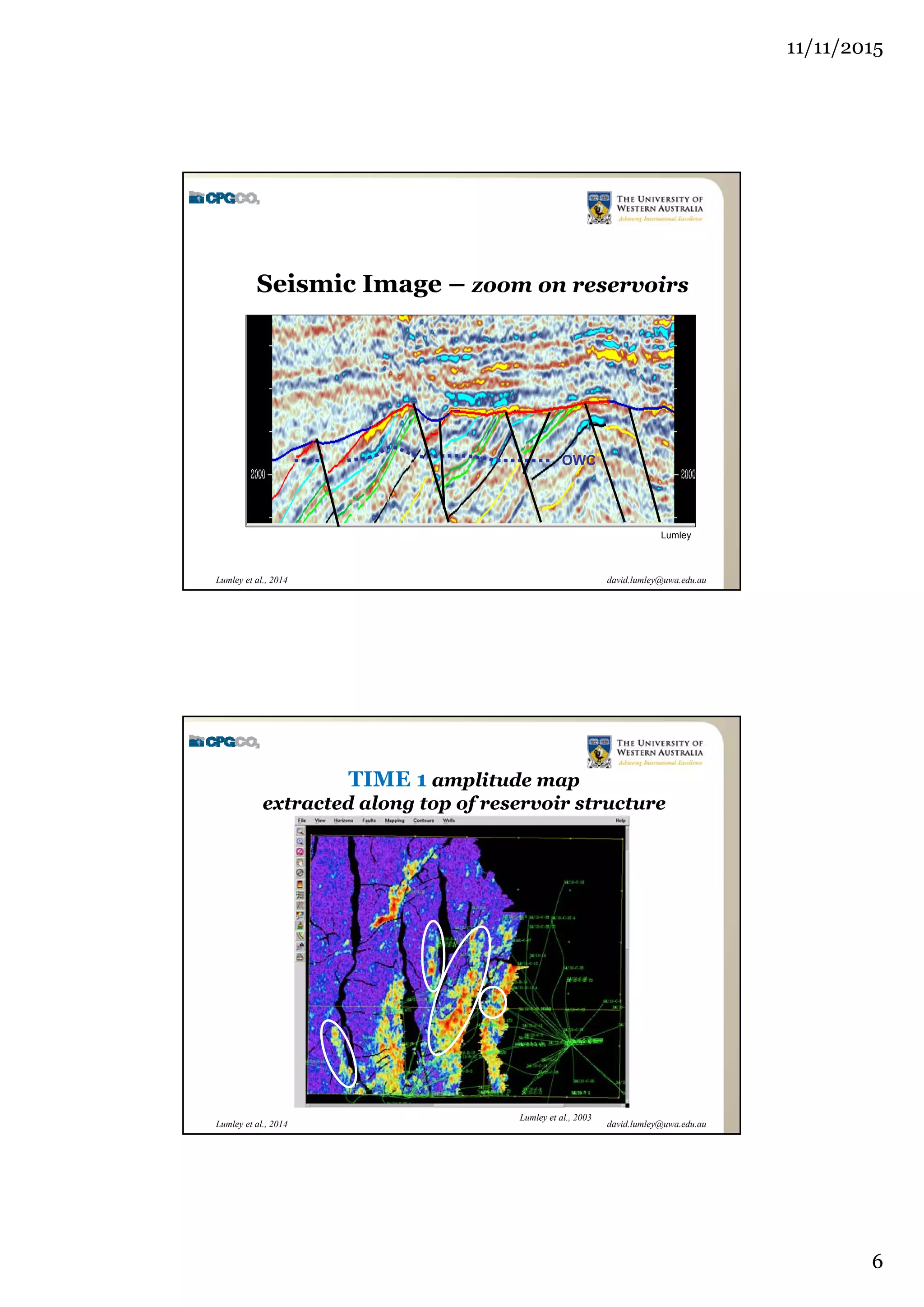
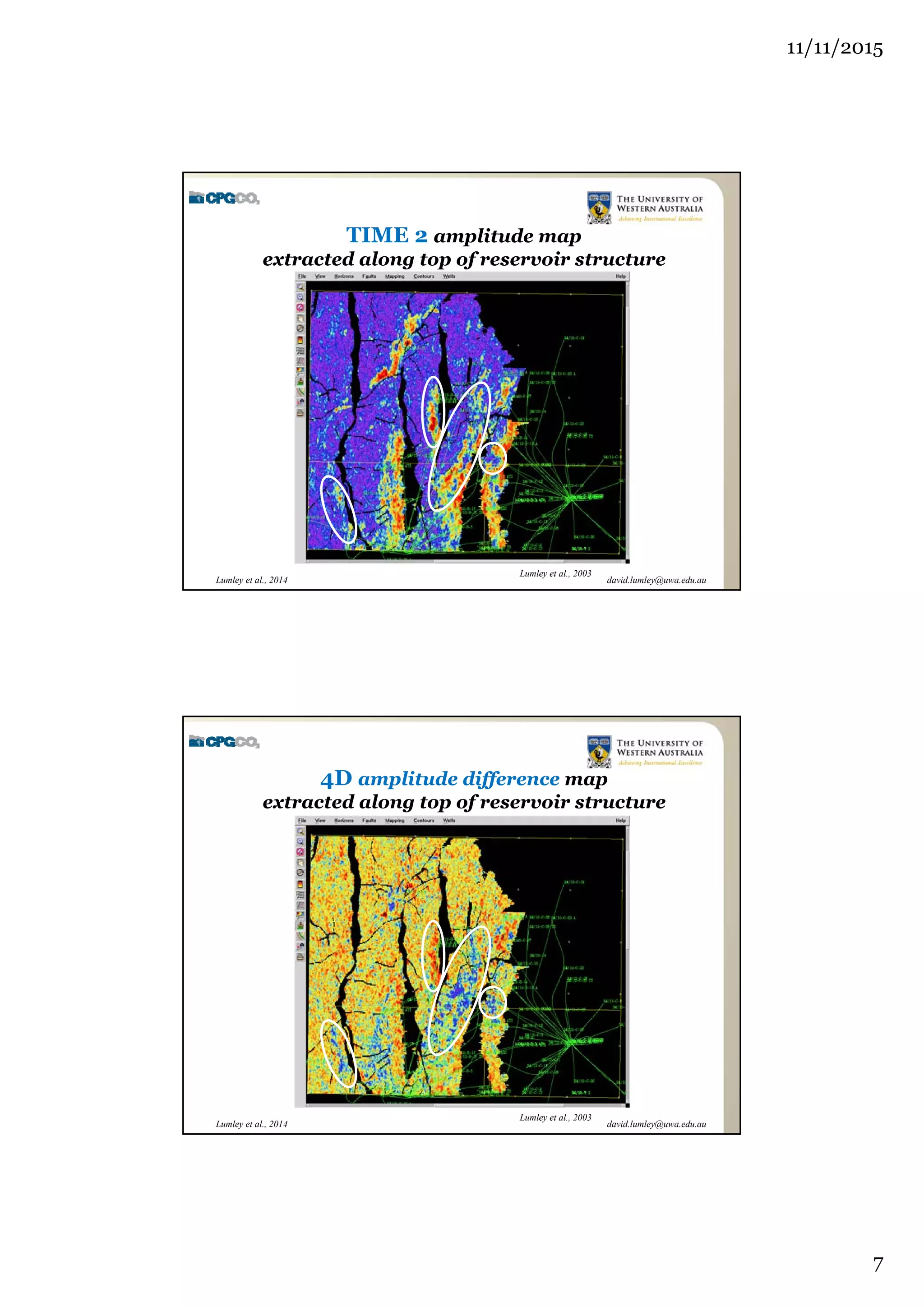
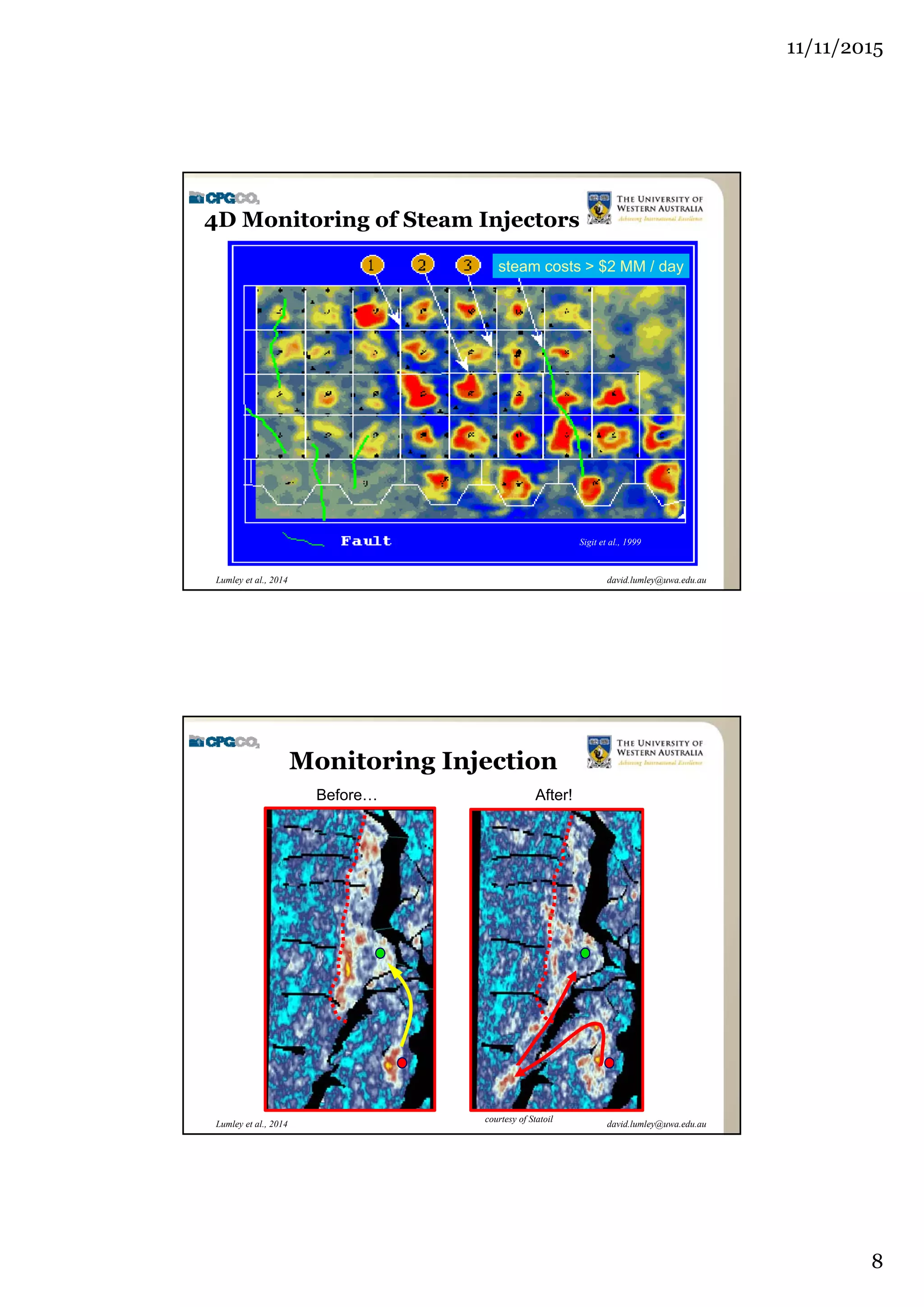
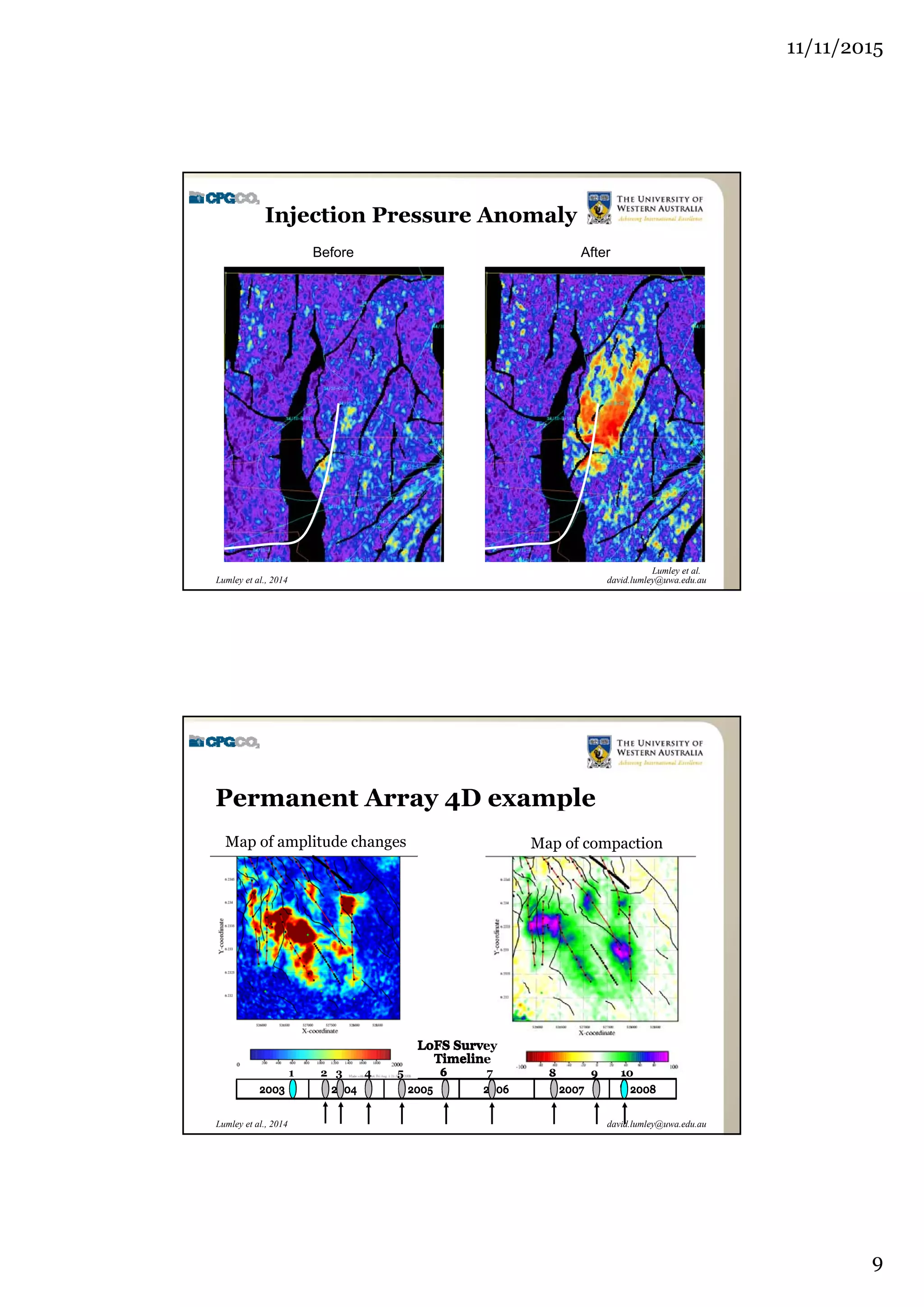
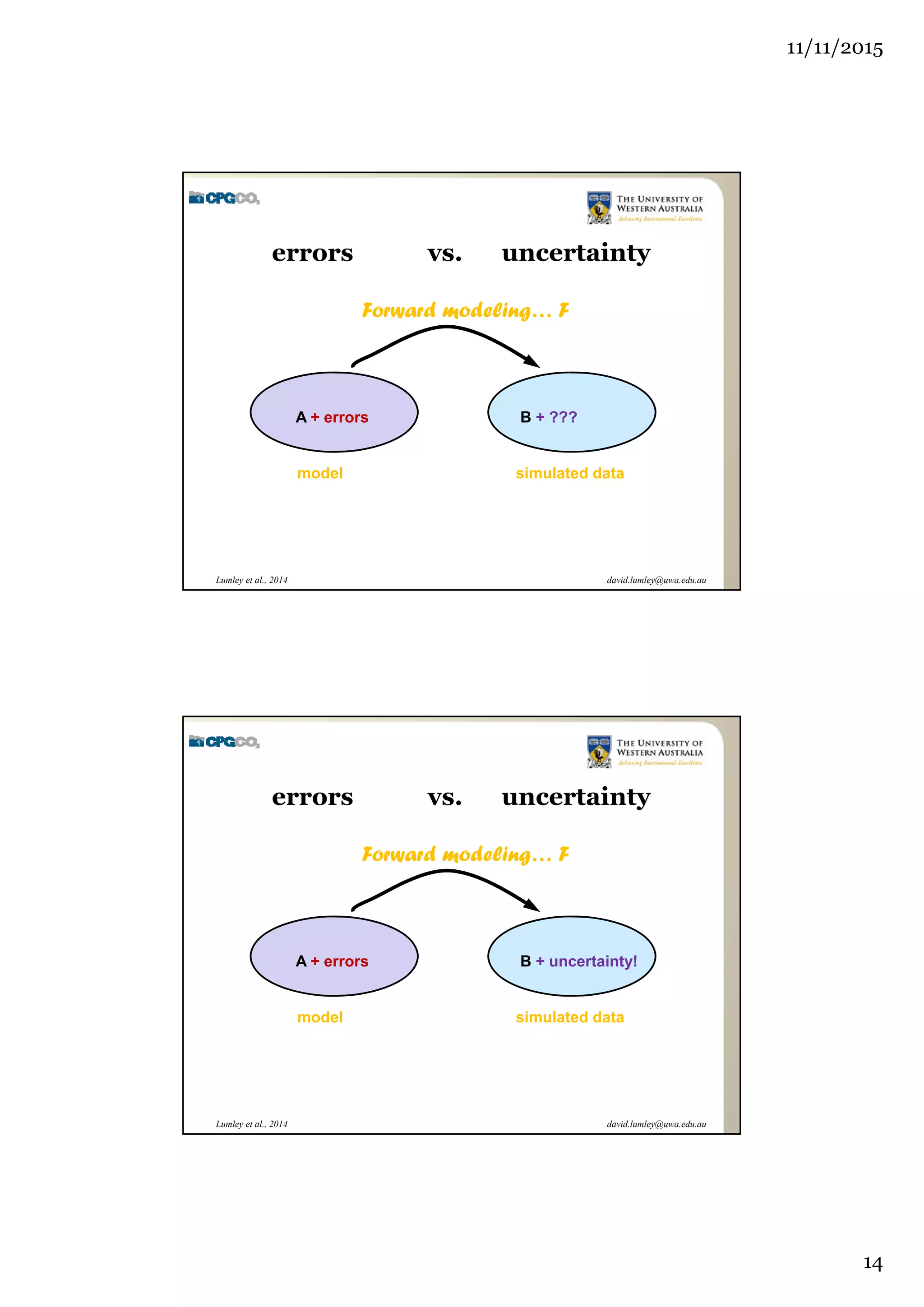
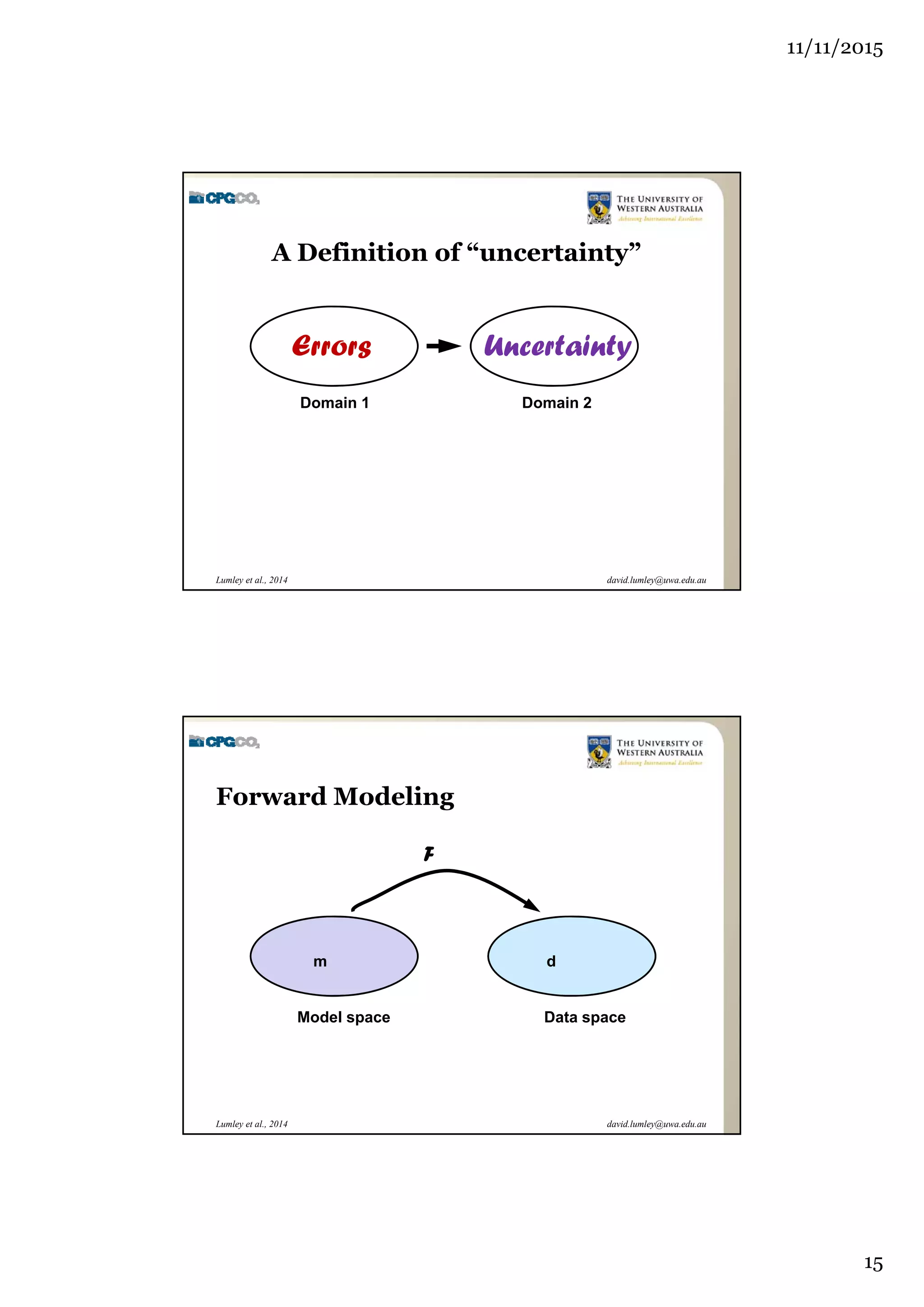
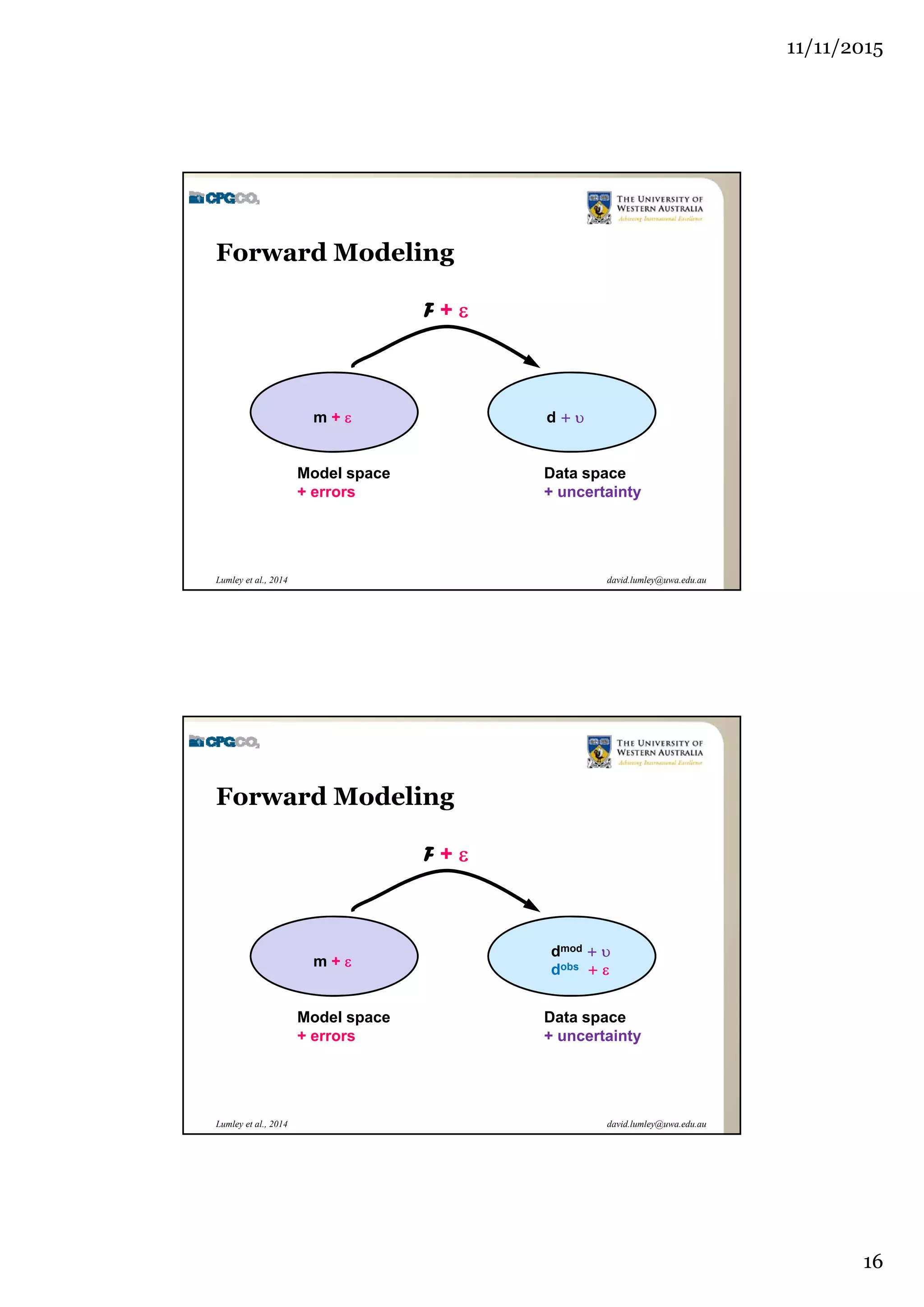
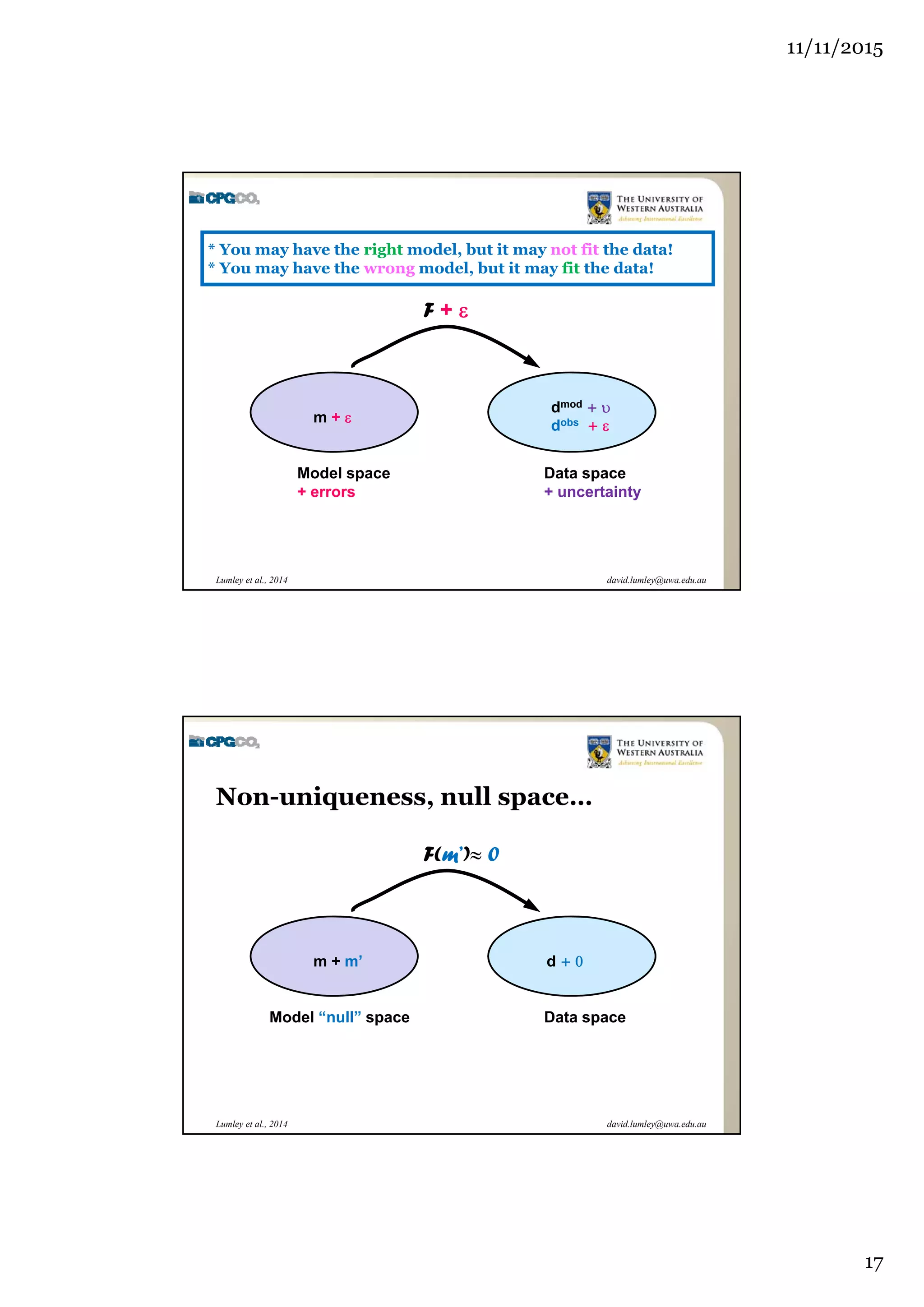
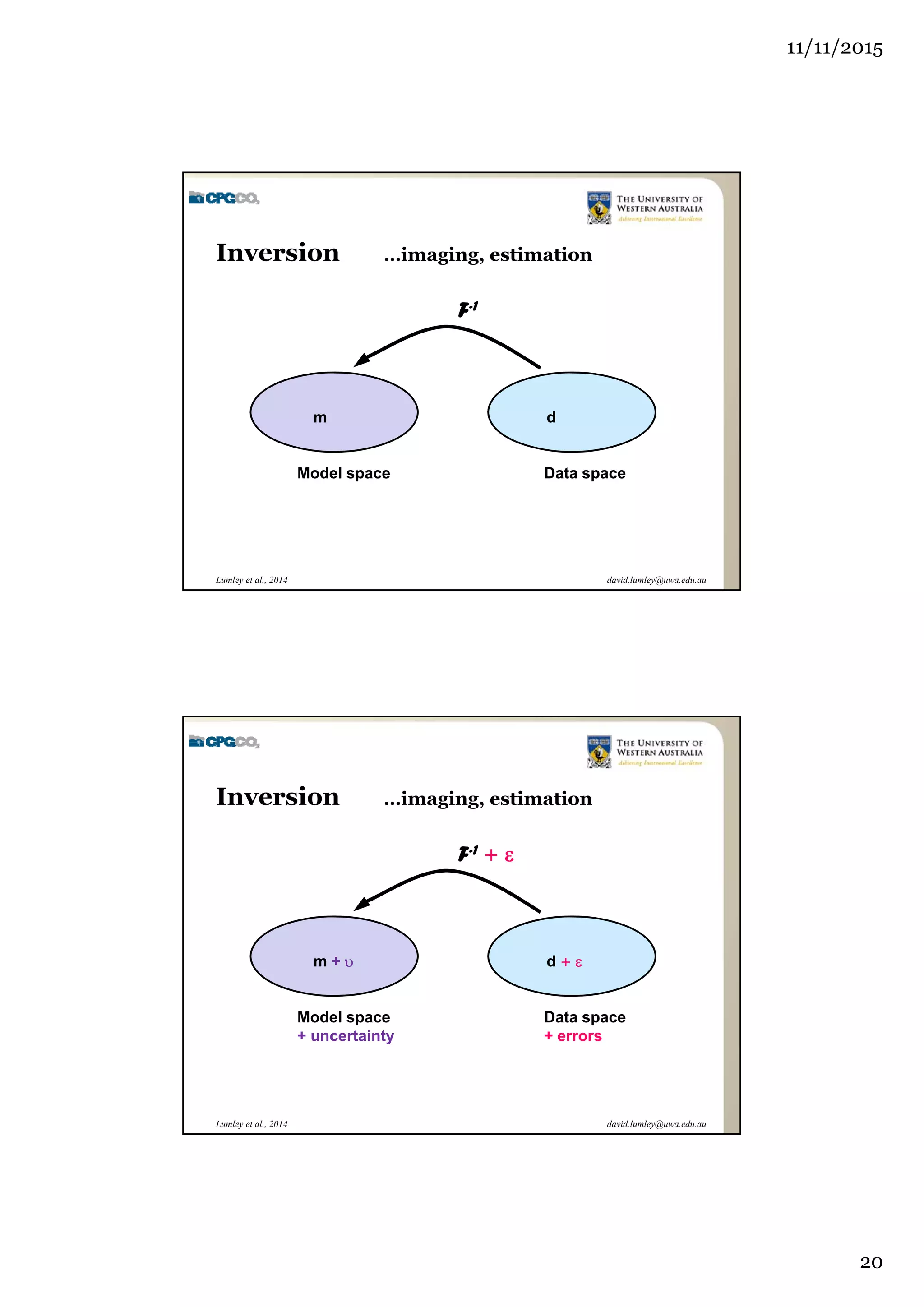
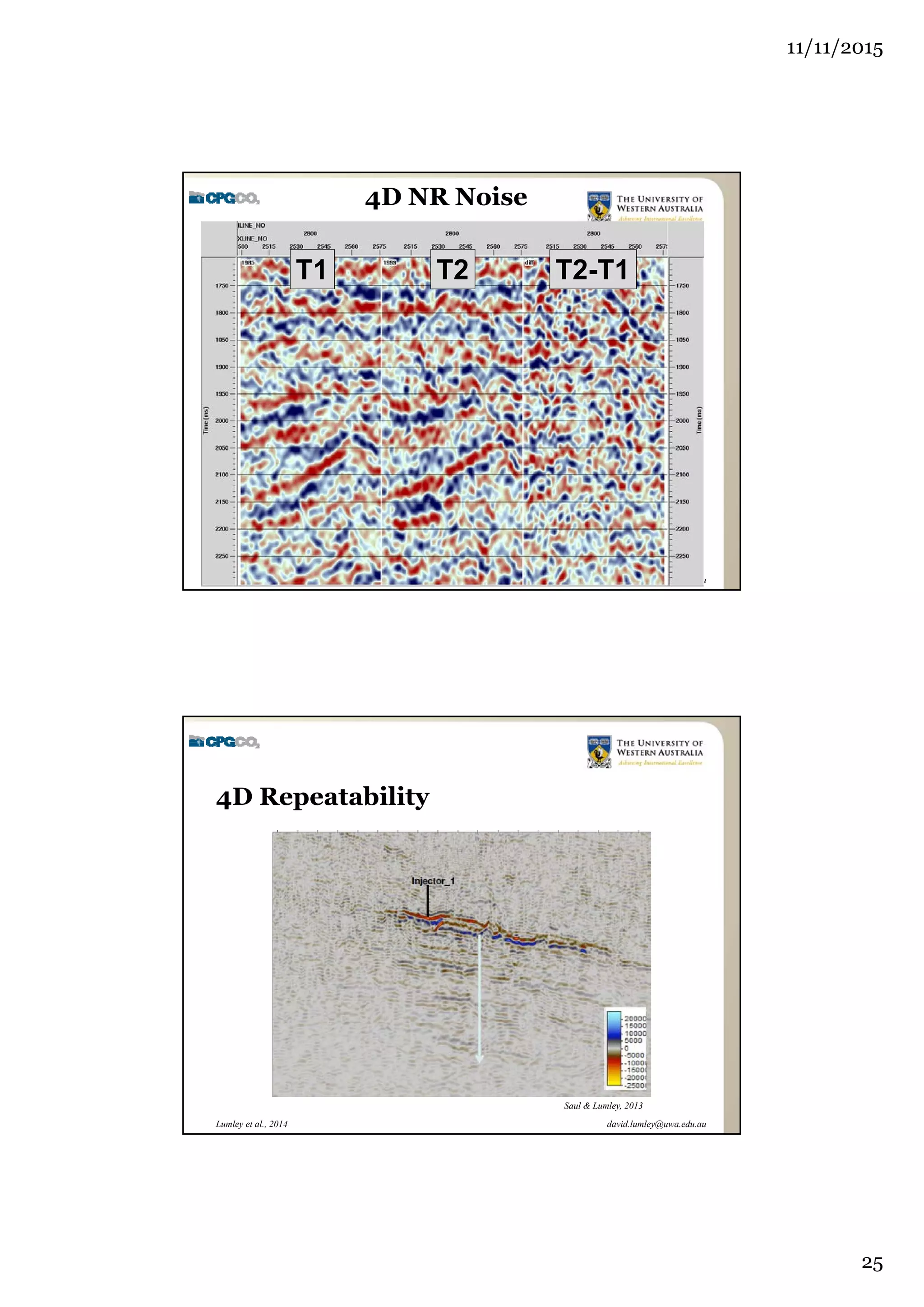
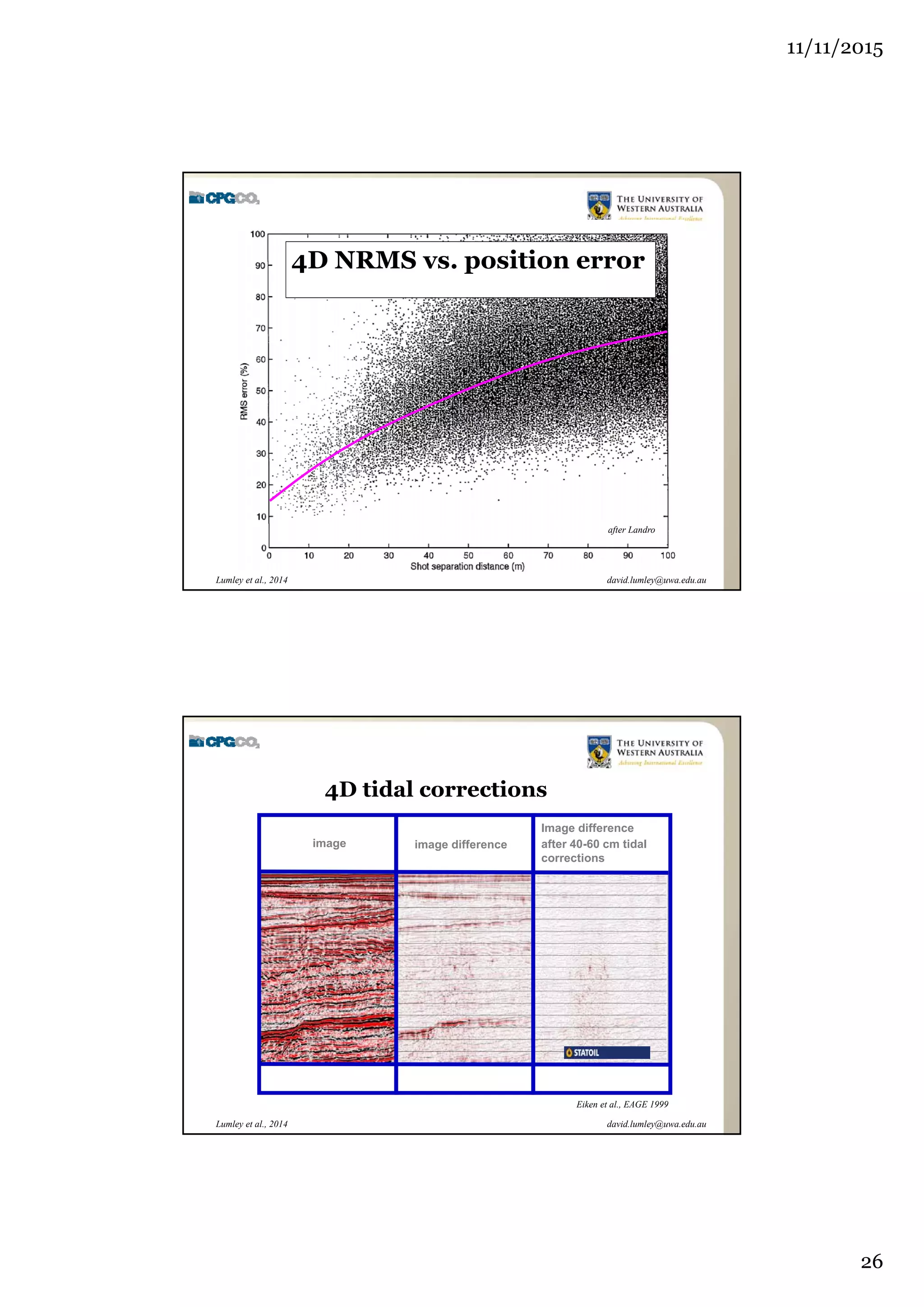
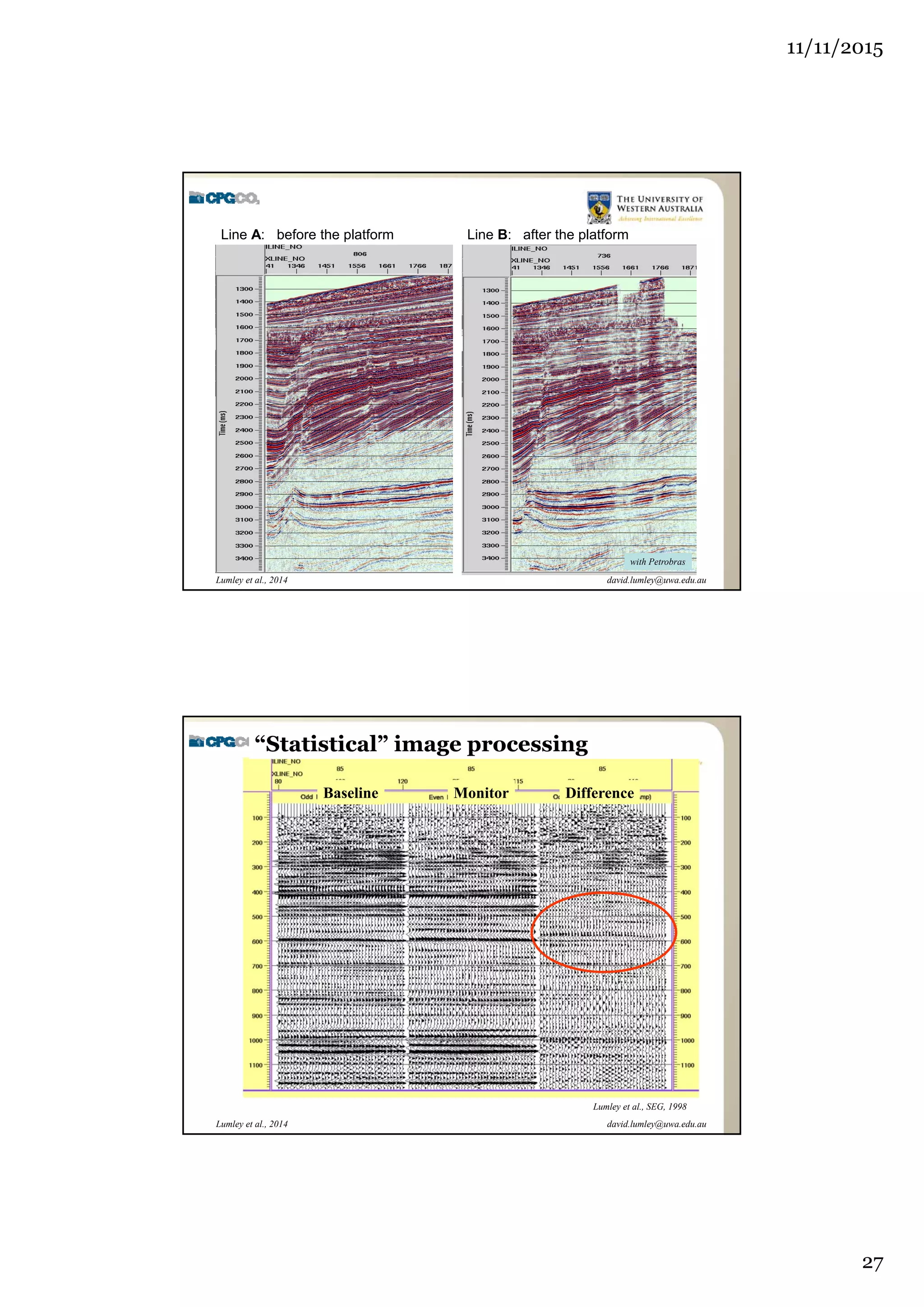
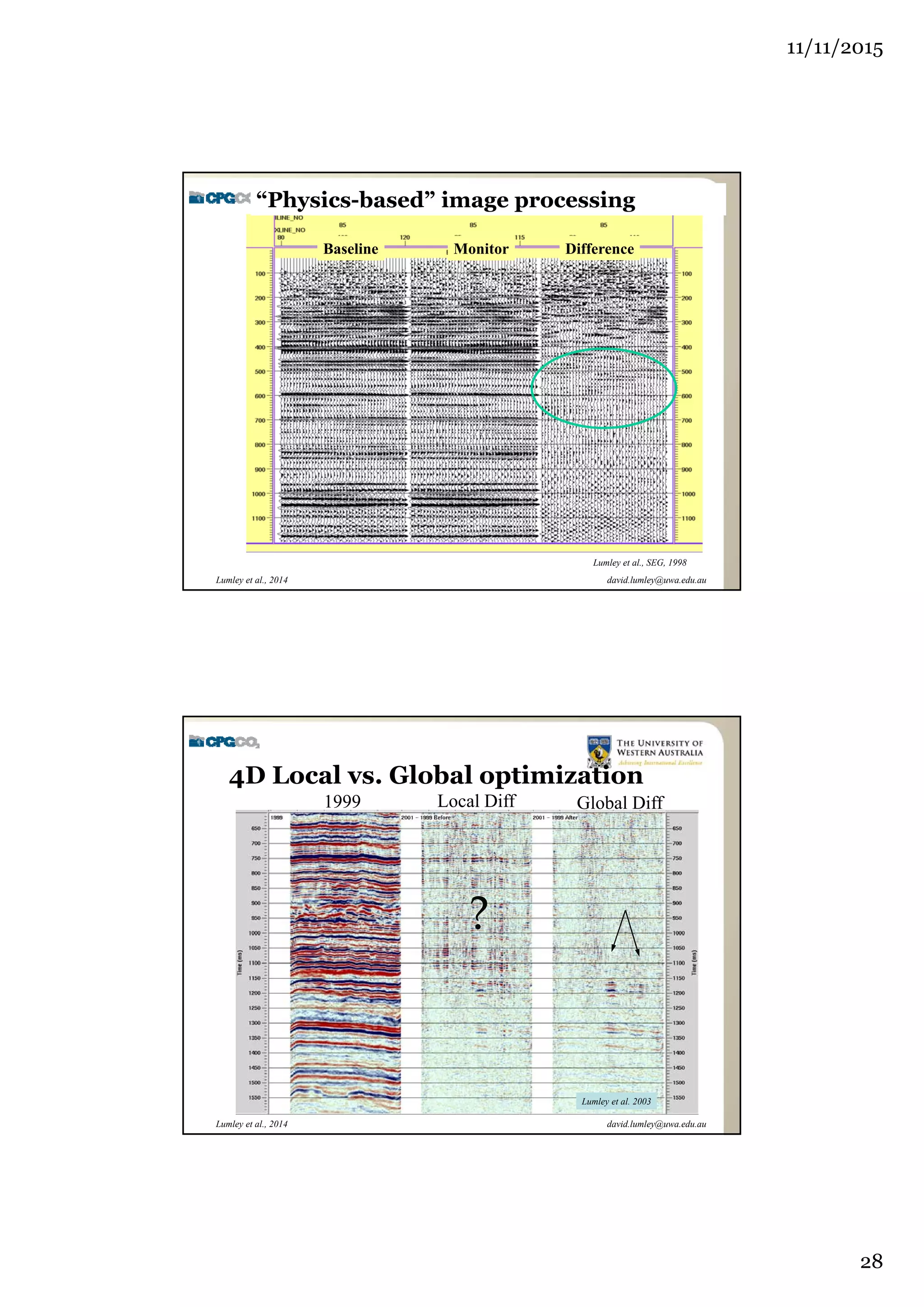
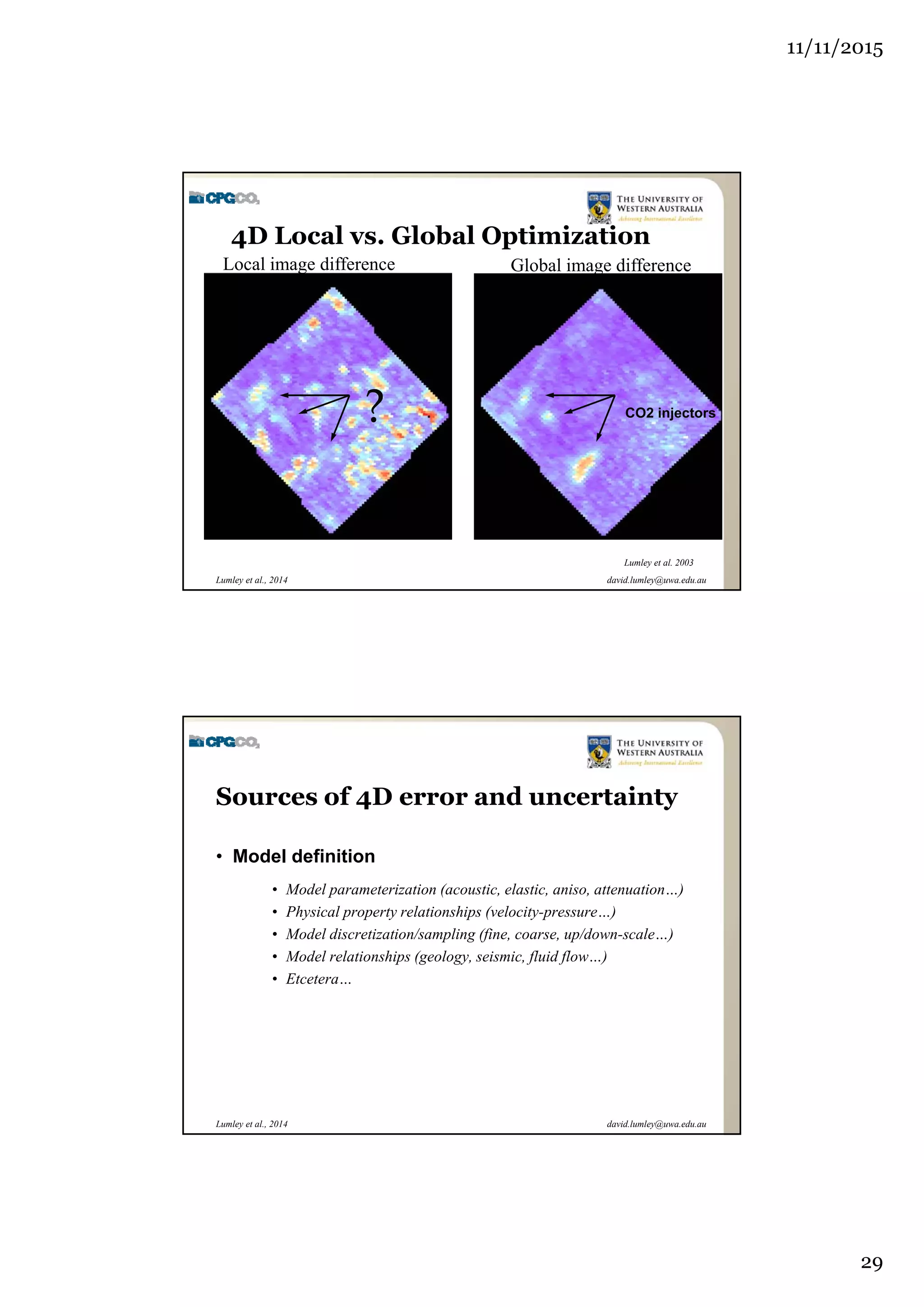
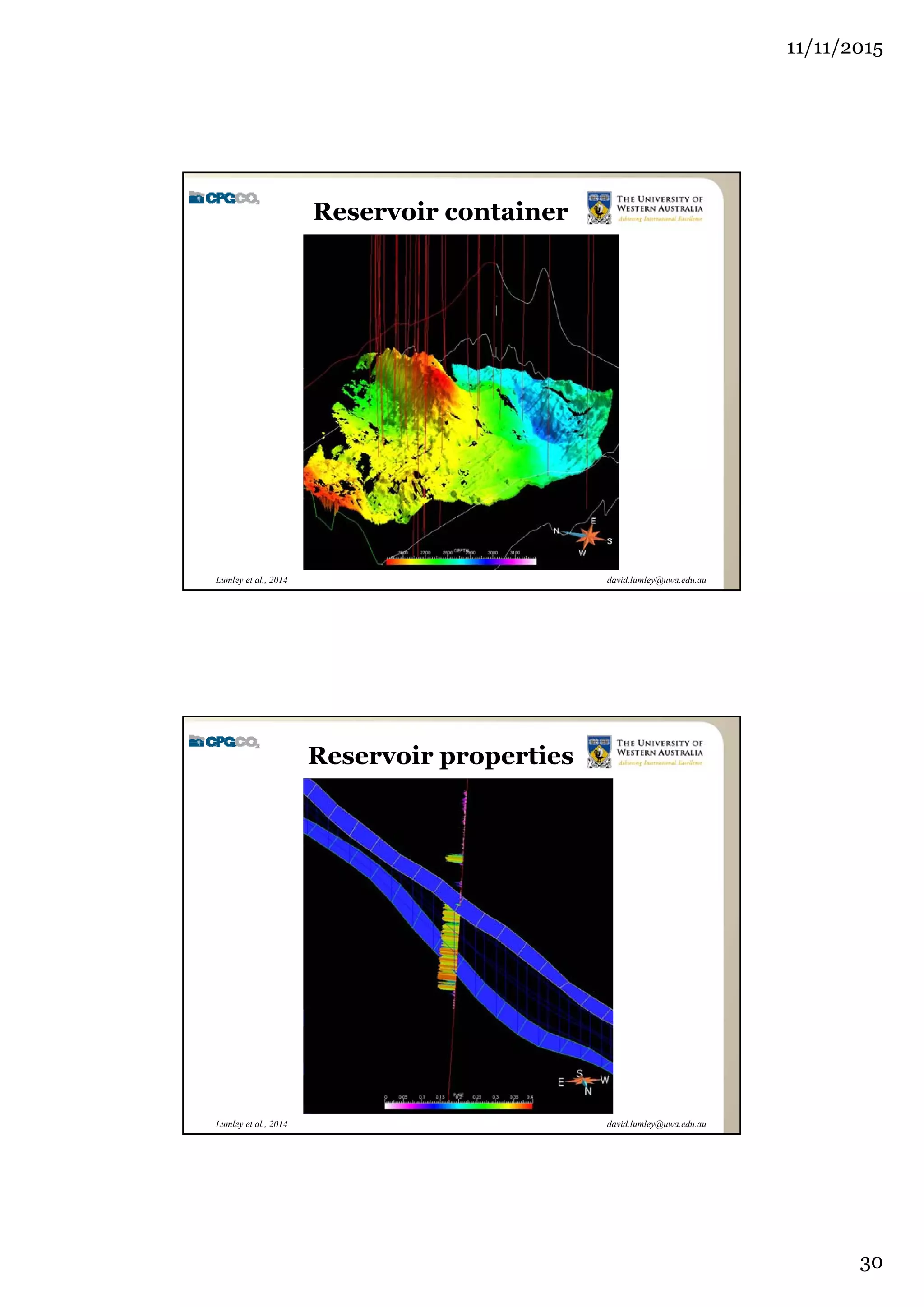
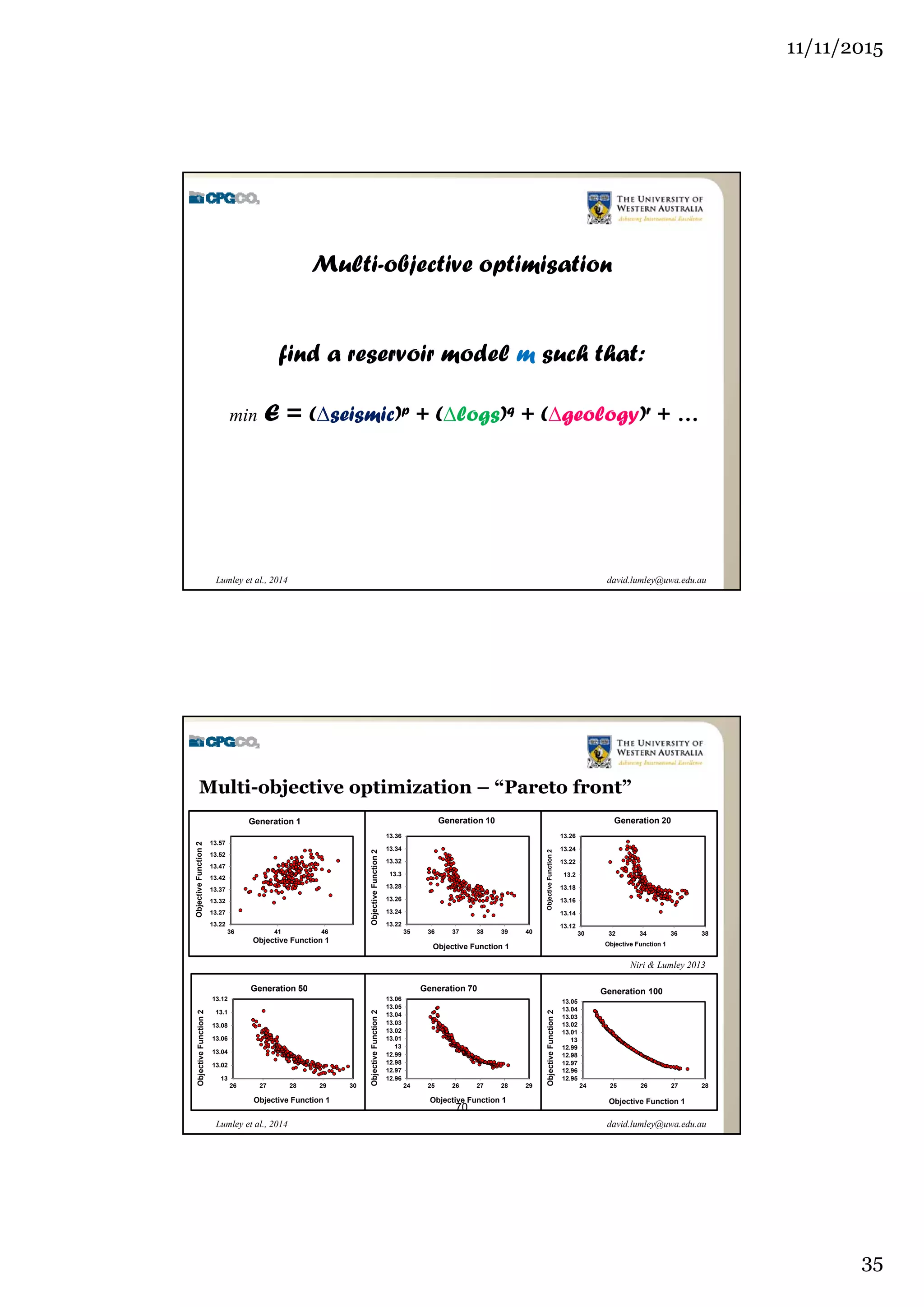
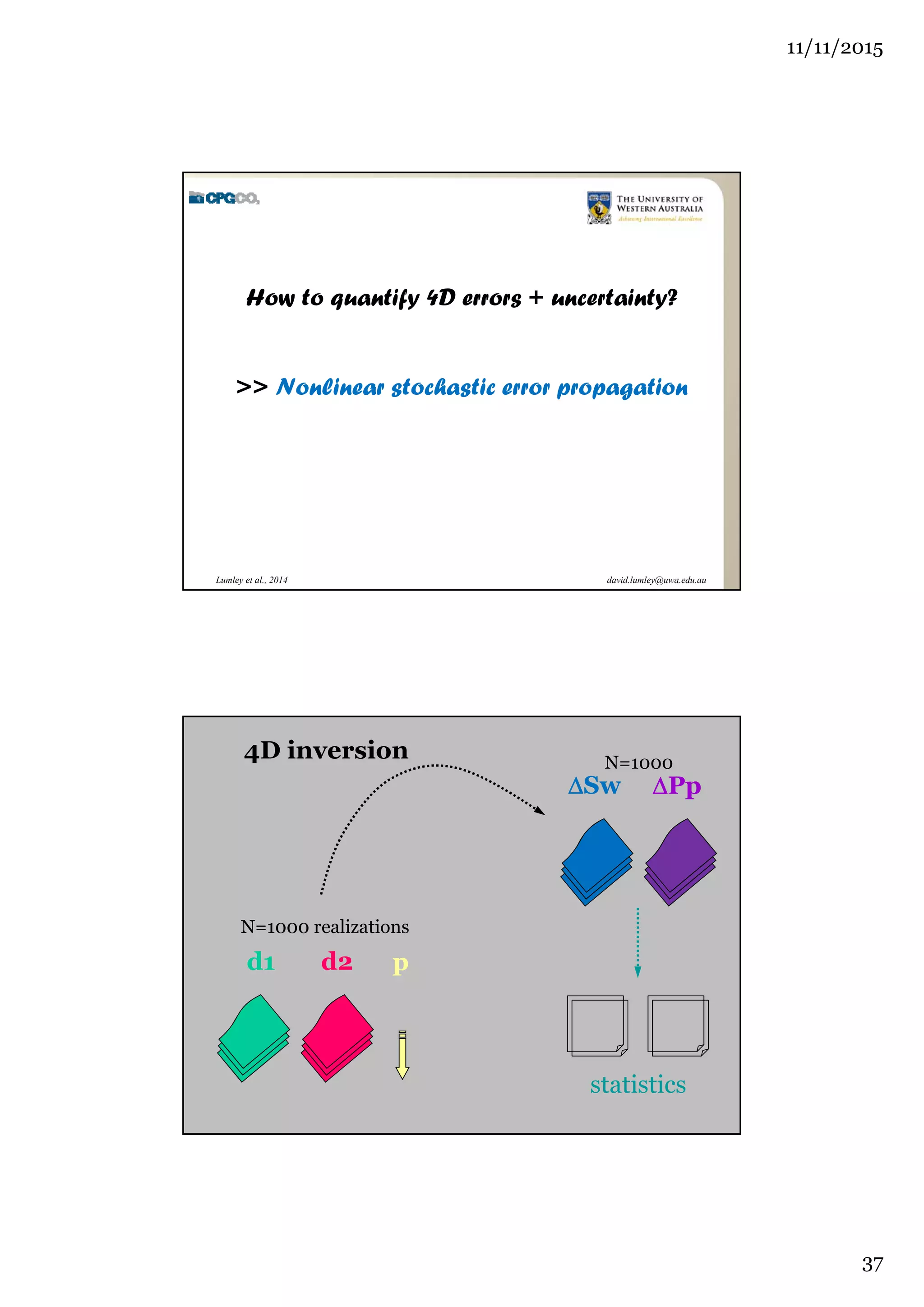
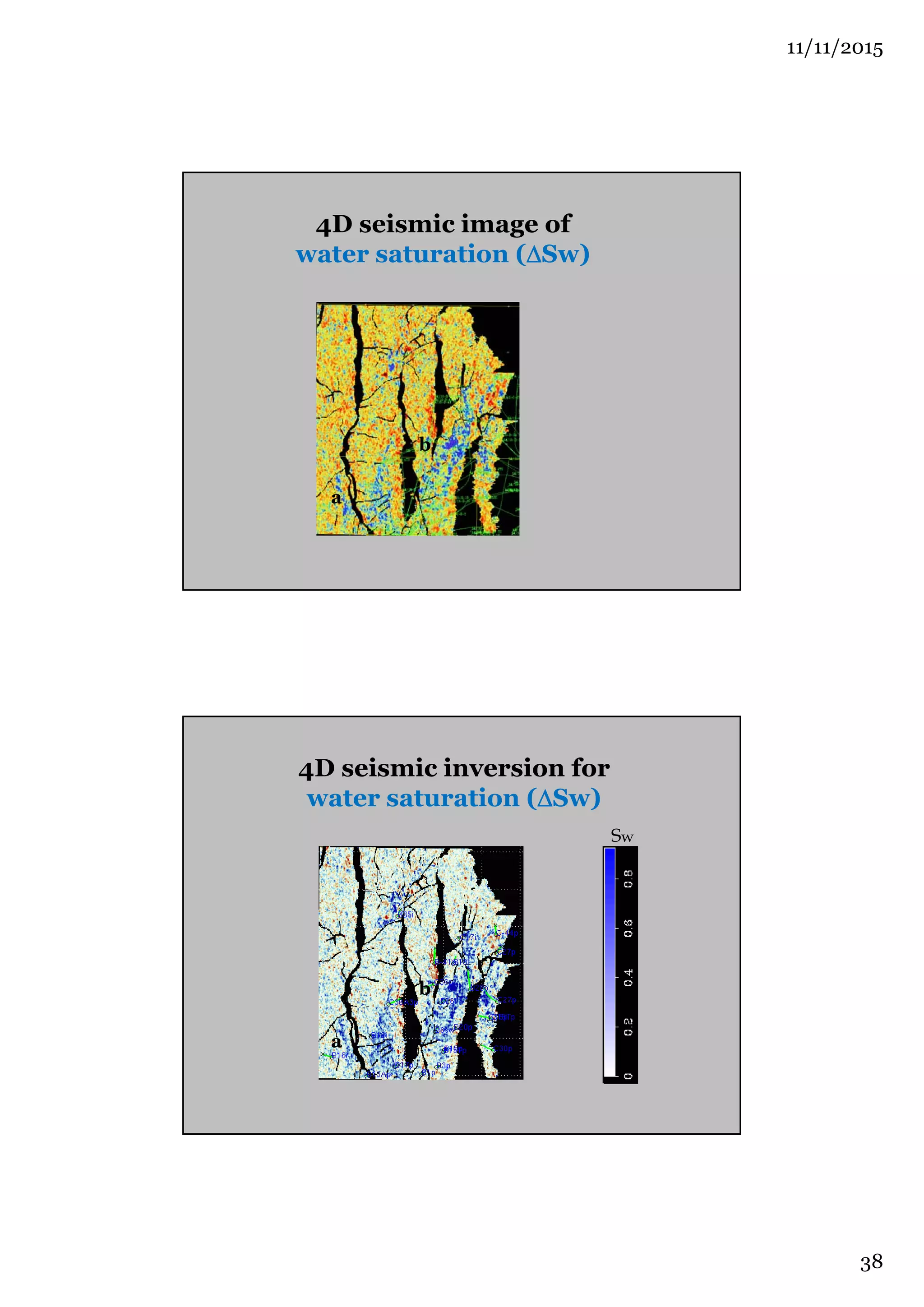
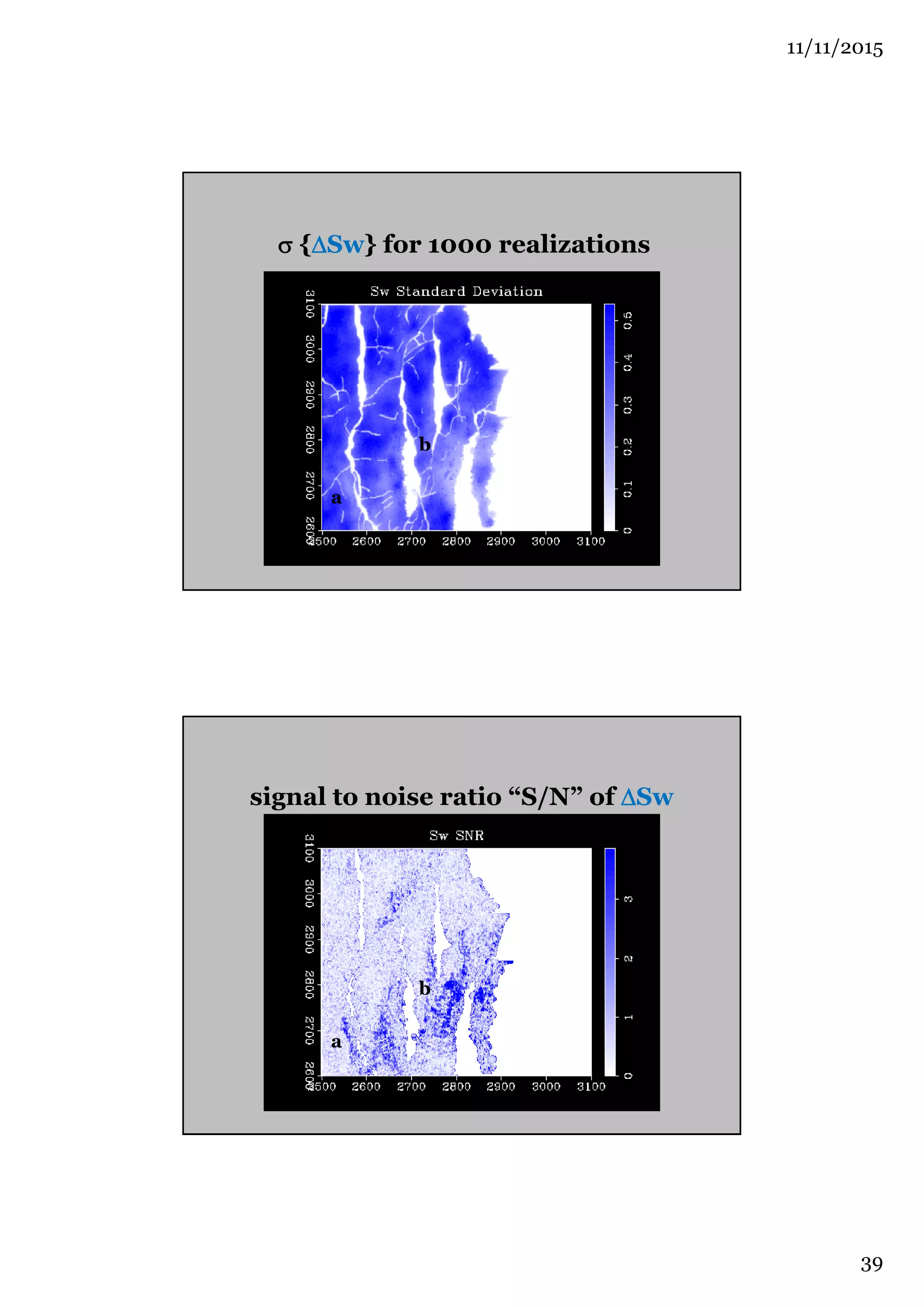
The document outlines the concept of 4D seismic monitoring, defining it as incorporating time into three-dimensional seismic data to track changes in reservoir properties. It discusses various sources of uncertainty and error in 4D seismic data, emphasizing the importance of nonlinear uncertainty analysis. Additionally, the document provides examples of seismic data visualization and the implications for reservoir monitoring and management.

Embed presentation

Downloaded 11 times
11/11/2015 1 david.lumley@uwa.edu.auLumley et al., 2014 Nonlinear Uncertainty Analysis: 4D Seismic reservoir monitoring Prof David Lumley + various colleagues and students over the years... UWA School of Physics; School of Earth & Environment david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
11/11/2015 2 david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 1D = f(x1): eg. well logs f(z) f = porosity, clay content, age facies, velocity, density…
11/11/2015 3 david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 2D = f(x1,x2): eg. maps, cross-sections (x,z) f = porosity, clay content, age structural depth, facies, reflectivity… Lumley et al. david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 3D = f(x,y,z): volumes (x,y,z) f = porosity, clay content, age velocity, reflectivity… Niri & Lumley, 2013
11/11/2015 4 david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 4D = f(x,y,z,t): hyper-cubes (x,y,z,t) f = porosity, clay content, age velocity, reflectivity… Lumley, 1995 david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
11/11/2015 5 david.lumley@uwa.edu.auLumley et al., 2014 Rock properties can change over time with fluids, stress, temperature etc… Duffaut et al.2011 david.lumley@uwa.edu.auLumley et al., 2014 Seismic Image – 2D cross-section Lumley
11/11/2015 6 david.lumley@uwa.edu.auLumley et al., 2014 Seismic Image – zoom on reservoirs OWC Lumley david.lumley@uwa.edu.auLumley et al., 2014 TIME 1 amplitude map extracted along top of reservoir structure Lumley et al., 2003
11/11/2015 7 david.lumley@uwa.edu.auLumley et al., 2014 TIME 2 amplitude map extracted along top of reservoir structure Lumley et al., 2003 david.lumley@uwa.edu.auLumley et al., 2014 4D amplitude difference map extracted along top of reservoir structure Lumley et al., 2003
11/11/2015 8 david.lumley@uwa.edu.auLumley et al., 2014 4D Monitoring of Steam Injectors Sigit et al., 1999 steam costs > $2 MM / day david.lumley@uwa.edu.auLumley et al., 2014 Before… After! courtesy of Statoil Monitoring Injection
11/11/2015 9 david.lumley@uwa.edu.auLumley et al., 2014 Injection Pressure Anomaly Before After Lumley et al., 2003Lumley et al. david.lumley@uwa.edu.auLumley et al., 2014 Permanent Array 4D example Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 10
11/11/2015 10 david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty input output A B transform
11/11/2015 11 david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty various data results A B workflow david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty earth model simulated data A B Forward modeling… F
11/11/2015 12 david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data image of the earth A B Imaging… F* david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data earth model A B Inversion… F-1
11/11/2015 13 david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data earth model Inversion… F-1 A + errors B + ??? david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data earth model Inversion… F-1 A + errors B + uncertainty!
11/11/2015 14 david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty model simulated data A + errors B + ??? Forward modeling… F david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty model simulated data A + errors B + uncertainty! Forward modeling… F
11/11/2015 15 david.lumley@uwa.edu.auLumley et al., 2014 Errors Uncertainty Domain 1 Domain 2 A Definition of “uncertainty” david.lumley@uwa.edu.auLumley et al., 2014 Forward Modeling Model space Data space m d F
11/11/2015 16 david.lumley@uwa.edu.auLumley et al., 2014 Model space + errors Data space + uncertainty m +  d +  F +  Forward Modeling david.lumley@uwa.edu.auLumley et al., 2014 Model space + errors Data space + uncertainty m +  dmod +  F +  dobs +  Forward Modeling
11/11/2015 17 david.lumley@uwa.edu.auLumley et al., 2014 * You may have the right model, but it may not fit the data! * You may have the wrong model, but it may fit the data! Model space + errors Data space + uncertainty m +  dmod +  F +  dobs +  david.lumley@uwa.edu.auLumley et al., 2014 Non-uniqueness, null space… Model “null” space Data space m + m’ d +  F(m’)≈ 0
11/11/2015 18 david.lumley@uwa.edu.auLumley et al., 2014 Example: low resolution data Gravity data david.lumley@uwa.edu.auLumley et al., 2014 “Mickey Mouse model” Gravity data
11/11/2015 19 david.lumley@uwa.edu.auLumley et al., 2014 Model “null” space Data space m + imi’ d +  F(m’)≈ 0 * There are infinitely many models that fit the data! david.lumley@uwa.edu.auLumley et al., 2014 Uncertainty ≠ Non-uniqueness
11/11/2015 20 david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space Data space F-1 m d david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space + uncertainty Data space + errors F-1 +  m +  d + 
11/11/2015 21 david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space + uncertainty + non-uniqueness Data space + errors F-1 +  m + + m’ d +  david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space + uncertainty + non-uniqueness * Regularization * * Model-shaping * Data space + errors F-1 +  m + + imi’ d + 
11/11/2015 22 david.lumley@uwa.edu.auLumley et al., 2014 “Mickey Mouse model” Gravity data david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
11/11/2015 23 david.lumley@uwa.edu.auLumley et al., 2014 “Closing the loop… history matching” Observed Data; t++ Inversion Estimated model; t++ Simulation Predicted data david.lumley@uwa.edu.auLumley et al., 2014 4D amplitude difference map extracted along top of reservoir structure Lumley et al., 2003
11/11/2015 24 david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • 4D Seismic data errors • Non-repeatable noise • Source-receiver positioning errors • Changes in the water column / near-surface / overburden • Changes in acquisition geometry • Changes in source-receiver characteristics • Non 4D-compliant processing flow • Etcetera… david.lumley@uwa.edu.auLumley et al., 2014 3D Noise data = “signal” + noise
11/11/2015 25 david.lumley@uwa.edu.auLumley et al., 2014 4D NR Noise T1 T2 T2-T1 david.lumley@uwa.edu.auLumley et al., 2014 4D Repeatability Saul & Lumley, 2013
11/11/2015 26 david.lumley@uwa.edu.auLumley et al., 2014 after Landro 4D NRMS vs. position error david.lumley@uwa.edu.auLumley et al., 2014 image image difference Image difference after 40-60 cm tidal corrections Eiken et al., EAGE 1999 4D tidal corrections
11/11/2015 27 david.lumley@uwa.edu.auLumley et al., 2014 Line A: before the platform Line B: after the platform with Petrobras david.lumley@uwa.edu.auLumley et al., 2014 “Statistical” image processing Baseline Monitor Difference Lumley et al., SEG, 1998
11/11/2015 28 david.lumley@uwa.edu.auLumley et al., 2014 Lumley et al., SEG, 1998 Baseline Monitor Difference “Physics-based” image processing david.lumley@uwa.edu.auLumley et al., 2014 1999 Local Diff Global Diff ? 4D Local vs. Global optimization Lumley et al. 2003
11/11/2015 29 david.lumley@uwa.edu.auLumley et al., 2014 Local image difference Global image difference CO2 injectors? Lumley et al. 2003 4D Local vs. Global Optimization david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Model definition • Model parameterization (acoustic, elastic, aniso, attenuation…) • Physical property relationships (velocity-pressure…) • Model discretization/sampling (fine, coarse, up/down-scale…) • Model relationships (geology, seismic, fluid flow…) • Etcetera…
11/11/2015 30 david.lumley@uwa.edu.auLumley et al., 2014 Reservoir container david.lumley@uwa.edu.auLumley et al., 2014 Reservoir properties
11/11/2015 31 david.lumley@uwa.edu.auLumley et al., 2014 Up/down scaling david.lumley@uwa.edu.auLumley et al., 2014 porosity clay fraction
11/11/2015 32 david.lumley@uwa.edu.auLumley et al., 2014 Rock physics param pdfs david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Physics (modeling/inversion operators/code) • Linear versus nonlinear • Acoustic, Elastic, Anisotropy, Attenuation… • Convolution, Raytracing, Finite Difference… • Algorithm implementations • Etcetera…
11/11/2015 33 david.lumley@uwa.edu.auLumley et al., 2014 4D FD elastic modeling david.lumley@uwa.edu.auLumley et al., 2014 1 layer CO2 Lumley et al., 2008 synth PSDM
11/11/2015 34 david.lumley@uwa.edu.auLumley et al., 2014 real PSTM 1 layer CO2 StatoilLumley et al., 2008 synth PSDM david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Optimization criteria (inversion/estimation) • Least squares (L2), Least absolute (L1), hybrid… • Optimal fit to data, amplitude, phase… • Multiple objectives, weighting schemes… • Inversion constraints (soft, hard, weighted…) • Optimization method (gradients, stochastic, MC, PSO, genetic…) • Resolution, Null space, Non-uniqueness… • Etcetera…
11/11/2015 35 david.lumley@uwa.edu.auLumley et al., 2014 Multi-objective optimisation find a reservoir model m such that: min E = (seismic)p + (logs)q + (geology)r + … david.lumley@uwa.edu.auLumley et al., 2014 13.22 13.27 13.32 13.37 13.42 13.47 13.52 13.57 36 41 46 ObjectiveFunction2 Objective Function 1 Generation 1 13.22 13.24 13.26 13.28 13.3 13.32 13.34 13.36 35 36 37 38 39 40 ObjectiveFunction2 Objective Function 1 Generation 10 13.12 13.14 13.16 13.18 13.2 13.22 13.24 13.26 30 32 34 36 38 ObjectiveFunction2 Objective Function 1 Generation 20 13 13.02 13.04 13.06 13.08 13.1 13.12 26 27 28 29 30 ObjectiveFunction2 Objective Function 1 Generation 50 12.96 12.97 12.98 12.99 13 13.01 13.02 13.03 13.04 13.05 13.06 24 25 26 27 28 29 ObjectiveFunction2 Objective Function 1 Generation 70 12.95 12.96 12.97 12.98 12.99 13 13.01 13.02 13.03 13.04 13.05 24 25 26 27 28 ObjectiveFunction2 Objective Function 1 Generation 100 Multi-objective optimization – “Pareto front” 70 Niri & Lumley 2013
11/11/2015 36 david.lumley@uwa.edu.auLumley et al., 2014 a) Reference Litho-facies model b) Before MO model updating c) After MO model updating  Average Mismatch error reduced from 36.5% to 14.6% Multi-objective optimization – “Pareto front” Niri & Lumley 2013 david.lumley@uwa.edu.auLumley et al., 2014 How to quantify 4D errors + uncertainty?
11/11/2015 37 david.lumley@uwa.edu.auLumley et al., 2014 How to quantify 4D errors + uncertainty? >> Nonlinear stochastic error propagation david.lumley@uwa.edu.auLumley et al., 2014 d1 d2 p N=1000 realizations Sw Pp 4D inversion statistics N=1000
11/11/2015 38 david.lumley@uwa.edu.auLumley et al., 2014 4D seismic image of water saturation (Sw) a b david.lumley@uwa.edu.auLumley et al., 2014 4D seismic inversion for water saturation (Sw) Sw a b
11/11/2015 39 david.lumley@uwa.edu.auLumley et al., 2014 {Sw} for 1000 realizations a b david.lumley@uwa.edu.auLumley et al., 2014 signal to noise ratio “S/N” of Sw a b
11/11/2015 40 david.lumley@uwa.edu.auLumley et al., 2014 Probability that Sw > 0.5 a b david.lumley@uwa.edu.auLumley et al., 2014 “Closing the loop… history matching” Observed Data; t++ Inversion Estimated model; t++ Simulation Predicted data
11/11/2015 41 david.lumley@uwa.edu.auLumley et al., 2014

More Related Content

PDF
First circular - Saying goodbye to a 3D Earth - - 3-7 August 2015
byThe University of Western Australia
 
PDF
John McGaughey - Towards integrated interpretation
byThe University of Western Australia
 
PPTX
Integration of geological and petrophysical constraints in geophysical joint ...
byThe University of Western Australia
 
PPTX
11-introduction on 4D Seismic method for monitoring.pptx
bysajjad1984
 
PDF
Program on Mathematical and Statistical Methods for Climate and the Earth Sys...
byThe Statistical and Applied Mathematical Sciences Institute
 
PDF
2014_Inv_Reid - An introduction to geophysical modelling.pdf
bymontserrat gardner
 
PDF
Data Visualization Workshop for Summer Interns
byZachary Labe
 
PPT
Elag workshop sessie 1 en 2 v10
byJeroen Rombouts
 
First circular - Saying goodbye to a 3D Earth - - 3-7 August 2015
byThe University of Western Australia
 
John McGaughey - Towards integrated interpretation
byThe University of Western Australia
 
Integration of geological and petrophysical constraints in geophysical joint ...
byThe University of Western Australia
 
11-introduction on 4D Seismic method for monitoring.pptx
bysajjad1984
 
Program on Mathematical and Statistical Methods for Climate and the Earth Sys...
byThe Statistical and Applied Mathematical Sciences Institute
 
2014_Inv_Reid - An introduction to geophysical modelling.pdf
bymontserrat gardner
 
Data Visualization Workshop for Summer Interns
byZachary Labe
 
Elag workshop sessie 1 en 2 v10
byJeroen Rombouts
 

Similar to David Lumley - 4D uncertainty - Nov 11, 2015

PDF
Timeseries Analysis And Inverse Theory For Geophysicists D Gibbons
bykollehalesz1
 
PDF
Wqtc2013 invest ofperformanceprobswitheds-20130910
byJohn B. Cook, PE, CEO
 
PPTX
Developing Computational Skills in the Sciences with Matlab Webinar 2017
bySERC at Carleton College
 
PPTX
Alice Gabriel - Pasc18 - Keynote
byAlice Gabriel
 
PPTX
Morocco2022_LocationProblem_Bondar.pptx
byouchenibrahim1
 
PDF
My Prize Winning Physics Poster from 2006
byDr. Catherine Sinclair She/Her
 
PDF
FUTURE TRENDS OF SEISMIC ANALYSIS
byStig-Arne Kristoffersen
 
Timeseries Analysis And Inverse Theory For Geophysicists D Gibbons
bykollehalesz1
 
Wqtc2013 invest ofperformanceprobswitheds-20130910
byJohn B. Cook, PE, CEO
 
Developing Computational Skills in the Sciences with Matlab Webinar 2017
bySERC at Carleton College
 
Alice Gabriel - Pasc18 - Keynote
byAlice Gabriel
 
Morocco2022_LocationProblem_Bondar.pptx
byouchenibrahim1
 
My Prize Winning Physics Poster from 2006
byDr. Catherine Sinclair She/Her
 
FUTURE TRENDS OF SEISMIC ANALYSIS
byStig-Arne Kristoffersen
 

More from The University of Western Australia

PPTX
Mark Jessell - Assessing and mitigating uncertainty in 3D geological models i...
byThe University of Western Australia
 
PDF
3D modelling and inversion in escript
byThe University of Western Australia
 
PPTX
3D model of a Ni-Cu-PGE ore body - Margaux Le Vaillant and June Hill (CSIRO)
byThe University of Western Australia
 
PDF
Innovative methods in geostatistics from studies in Chilean copper deposits -...
byThe University of Western Australia
 
PPTX
Mark Jessell - The topology of geology
byThe University of Western Australia
 
PPTX
Francky Fouedjio - Synthetic data analytics
byThe University of Western Australia
 
PPT
Peter Schaubs - GeoLena November 11, 2015
byThe University of Western Australia
 
PPTX
Synthetic geology dataset - June Hill CSIRO
byThe University of Western Australia
 
PDF
Scenario Testing and Sensitivity Analysis for 3-D Kinematic Models and Geophy...
byThe University of Western Australia
 
PPTX
Cell Based Associations - Evren Pakyuz-Charrier (CET/UWA)
byThe University of Western Australia
 
PPTX
3D Geoscience at GSWA - Klaus Gessner (GSWA)
byThe University of Western Australia
 
PPTX
Uncertainty in Geological Mapping - Lachlan Grose (Monash Uni.)
byThe University of Western Australia
 
PPTX
Gautier Laurent - Implicit Modelling and volume deformation
byThe University of Western Australia
 
PPTX
20 years of 3D structural modelling - Laurent Ailleres (Monash University)
byThe University of Western Australia
 
PDF
  Information Theory and the Analysis of Uncertainties in a Spatial Geologi...
byThe University of Western Australia
 
PDF
Mark Jessell - Next Generation 3D Modelling
byThe University of Western Australia
 
PDF
Florian Wellmann: Uncertainties in 3D Models
byThe University of Western Australia
 
Mark Jessell - Assessing and mitigating uncertainty in 3D geological models i...
byThe University of Western Australia
 
3D modelling and inversion in escript
byThe University of Western Australia
 
3D model of a Ni-Cu-PGE ore body - Margaux Le Vaillant and June Hill (CSIRO)
byThe University of Western Australia
 
Innovative methods in geostatistics from studies in Chilean copper deposits -...
byThe University of Western Australia
 
Mark Jessell - The topology of geology
byThe University of Western Australia
 
Francky Fouedjio - Synthetic data analytics
byThe University of Western Australia
 
Peter Schaubs - GeoLena November 11, 2015
byThe University of Western Australia
 
Synthetic geology dataset - June Hill CSIRO
byThe University of Western Australia
 
Scenario Testing and Sensitivity Analysis for 3-D Kinematic Models and Geophy...
byThe University of Western Australia
 
Cell Based Associations - Evren Pakyuz-Charrier (CET/UWA)
byThe University of Western Australia
 
3D Geoscience at GSWA - Klaus Gessner (GSWA)
byThe University of Western Australia
 
Uncertainty in Geological Mapping - Lachlan Grose (Monash Uni.)
byThe University of Western Australia
 
Gautier Laurent - Implicit Modelling and volume deformation
byThe University of Western Australia
 
20 years of 3D structural modelling - Laurent Ailleres (Monash University)
byThe University of Western Australia
 
  Information Theory and the Analysis of Uncertainties in a Spatial Geologi...
byThe University of Western Australia
 
Mark Jessell - Next Generation 3D Modelling
byThe University of Western Australia
 
Florian Wellmann: Uncertainties in 3D Models
byThe University of Western Australia
 

Recently uploaded

PDF
634987849-Class-12-Physics-Formula-Sheet.pdf
by123456789035
 
PPTX
Physical Science SHS 24.1 Special and General Theory of Relativity.pptx
byJessonSuaga1
 
PDF
Cloud microphysical processes: graduate lecture slides on Cloud Physics UNR C...
byDDM
 
PDF
Ch3-phys701-Maram optics for 1234566.pdf
byssuserd90459
 
PPTX
Copy of quiz bee questions for ISKOWIZARD-2019.pptx
byMaryJoyGEvangelista
 
PDF
Amino acid cost and supply chain analysis for cultivated meat
byThe Good Food Institute
 
PDF
Detection of disk-jet coprecession in a tidaldisruption event
bySérgio Sacani
 
PDF
Enhancing the Role of Knowledge Holders in the UN CBD: Pioneering Capacity-Bu...
bypensoftservices
 
PPTX
Quality of irrigation water and brackish water management.pptx
bySaurabh Upadhyay
 
PDF
BP504T PHARMACOGNOSY UNIT 02 SUMMARY PART 01
byAnubhav Gupta
 
PPTX
Matrix-2025092302163983839339933993929.pptx
byStevenSantoso9
 
PPTX
ASTHMA. CHE (1).pptx- diagnosis and management
bymbchb420221
 
PDF
The Bioland Tool for National Clearing-House Mechanism Portals: Introduction ...
bypensoftservices
 
PPTX
721487259-Caring-for-Network-and-Computer-Hardware.pptx
byBizunehgetu
 
PPT
DLC911_Feedback.ppt for grade 10 students
byROLANARIBATO3
 
PDF
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
PPTX
Advances in Monoclonal Antibody.pptxaaaaa
bya7medelmnifi
 
PPTX
CLASSIFICATION OF LIVING ORGANISMS: THE THREE DOMAINS OF LIFE
byHOME
 
PDF
MOT , VBT , Ionic Bonding, VSPER Theory BSc 1st Sem Inorganic Chemistry Irfan...
byWorld of Wisdom
 
PDF
Lecture 7 Extra oral examination power point.pdf
byAbdullahAli461415
 
634987849-Class-12-Physics-Formula-Sheet.pdf
by123456789035
 
Physical Science SHS 24.1 Special and General Theory of Relativity.pptx
byJessonSuaga1
 
Cloud microphysical processes: graduate lecture slides on Cloud Physics UNR C...
byDDM
 
Ch3-phys701-Maram optics for 1234566.pdf
byssuserd90459
 
Copy of quiz bee questions for ISKOWIZARD-2019.pptx
byMaryJoyGEvangelista
 
Amino acid cost and supply chain analysis for cultivated meat
byThe Good Food Institute
 
Detection of disk-jet coprecession in a tidaldisruption event
bySérgio Sacani
 
Enhancing the Role of Knowledge Holders in the UN CBD: Pioneering Capacity-Bu...
bypensoftservices
 
Quality of irrigation water and brackish water management.pptx
bySaurabh Upadhyay
 
BP504T PHARMACOGNOSY UNIT 02 SUMMARY PART 01
byAnubhav Gupta
 
Matrix-2025092302163983839339933993929.pptx
byStevenSantoso9
 
ASTHMA. CHE (1).pptx- diagnosis and management
bymbchb420221
 
The Bioland Tool for National Clearing-House Mechanism Portals: Introduction ...
bypensoftservices
 
721487259-Caring-for-Network-and-Computer-Hardware.pptx
byBizunehgetu
 
DLC911_Feedback.ppt for grade 10 students
byROLANARIBATO3
 
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
Advances in Monoclonal Antibody.pptxaaaaa
bya7medelmnifi
 
CLASSIFICATION OF LIVING ORGANISMS: THE THREE DOMAINS OF LIFE
byHOME
 
MOT , VBT , Ionic Bonding, VSPER Theory BSc 1st Sem Inorganic Chemistry Irfan...
byWorld of Wisdom
 
Lecture 7 Extra oral examination power point.pdf
byAbdullahAli461415
 

David Lumley - 4D uncertainty - Nov 11, 2015

  • 1.
    11/11/2015 1 david.lumley@uwa.edu.auLumley et al.,2014 Nonlinear Uncertainty Analysis: 4D Seismic reservoir monitoring Prof David Lumley + various colleagues and students over the years... UWA School of Physics; School of Earth & Environment david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
  • 2.
    11/11/2015 2 david.lumley@uwa.edu.auLumley et al.,2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 1D = f(x1): eg. well logs f(z) f = porosity, clay content, age facies, velocity, density…
  • 3.
    11/11/2015 3 david.lumley@uwa.edu.auLumley et al.,2014 Geophysics definition of “4D” 2D = f(x1,x2): eg. maps, cross-sections (x,z) f = porosity, clay content, age structural depth, facies, reflectivity… Lumley et al. david.lumley@uwa.edu.auLumley et al., 2014 Geophysics definition of “4D” 3D = f(x,y,z): volumes (x,y,z) f = porosity, clay content, age velocity, reflectivity… Niri & Lumley, 2013
  • 4.
    11/11/2015 4 david.lumley@uwa.edu.auLumley et al.,2014 Geophysics definition of “4D” 4D = f(x,y,z,t): hyper-cubes (x,y,z,t) f = porosity, clay content, age velocity, reflectivity… Lumley, 1995 david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
  • 5.
    11/11/2015 5 david.lumley@uwa.edu.auLumley et al.,2014 Rock properties can change over time with fluids, stress, temperature etc… Duffaut et al.2011 david.lumley@uwa.edu.auLumley et al., 2014 Seismic Image – 2D cross-section Lumley
  • 6.
    11/11/2015 6 david.lumley@uwa.edu.auLumley et al.,2014 Seismic Image – zoom on reservoirs OWC Lumley david.lumley@uwa.edu.auLumley et al., 2014 TIME 1 amplitude map extracted along top of reservoir structure Lumley et al., 2003
  • 7.
    11/11/2015 7 david.lumley@uwa.edu.auLumley et al.,2014 TIME 2 amplitude map extracted along top of reservoir structure Lumley et al., 2003 david.lumley@uwa.edu.auLumley et al., 2014 4D amplitude difference map extracted along top of reservoir structure Lumley et al., 2003
  • 8.
    11/11/2015 8 david.lumley@uwa.edu.auLumley et al.,2014 4D Monitoring of Steam Injectors Sigit et al., 1999 steam costs > $2 MM / day david.lumley@uwa.edu.auLumley et al., 2014 Before… After! courtesy of Statoil Monitoring Injection
  • 9.
    11/11/2015 9 david.lumley@uwa.edu.auLumley et al.,2014 Injection Pressure Anomaly Before After Lumley et al., 2003Lumley et al. david.lumley@uwa.edu.auLumley et al., 2014 Permanent Array 4D example Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 1 0 Map of amplitude changes Map of compaction 2003 2004 2005 200820072006 LoFS Survey Timeline 1 2 3 4 5 6 7 8 9 10
  • 10.
    11/11/2015 10 david.lumley@uwa.edu.auLumley et al.,2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty input output A B transform
  • 11.
    11/11/2015 11 david.lumley@uwa.edu.auLumley et al.,2014 errors vs. uncertainty various data results A B workflow david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty earth model simulated data A B Forward modeling… F
  • 12.
    11/11/2015 12 david.lumley@uwa.edu.auLumley et al.,2014 errors vs. uncertainty geophysics data image of the earth A B Imaging… F* david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data earth model A B Inversion… F-1
  • 13.
    11/11/2015 13 david.lumley@uwa.edu.auLumley et al.,2014 errors vs. uncertainty geophysics data earth model Inversion… F-1 A + errors B + ??? david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty geophysics data earth model Inversion… F-1 A + errors B + uncertainty!
  • 14.
    11/11/2015 14 david.lumley@uwa.edu.auLumley et al.,2014 errors vs. uncertainty model simulated data A + errors B + ??? Forward modeling… F david.lumley@uwa.edu.auLumley et al., 2014 errors vs. uncertainty model simulated data A + errors B + uncertainty! Forward modeling… F
  • 15.
    11/11/2015 15 david.lumley@uwa.edu.auLumley et al.,2014 Errors Uncertainty Domain 1 Domain 2 A Definition of “uncertainty” david.lumley@uwa.edu.auLumley et al., 2014 Forward Modeling Model space Data space m d F
  • 16.
    11/11/2015 16 david.lumley@uwa.edu.auLumley et al.,2014 Model space + errors Data space + uncertainty m +  d +  F +  Forward Modeling david.lumley@uwa.edu.auLumley et al., 2014 Model space + errors Data space + uncertainty m +  dmod +  F +  dobs +  Forward Modeling
  • 17.
    11/11/2015 17 david.lumley@uwa.edu.auLumley et al.,2014 * You may have the right model, but it may not fit the data! * You may have the wrong model, but it may fit the data! Model space + errors Data space + uncertainty m +  dmod +  F +  dobs +  david.lumley@uwa.edu.auLumley et al., 2014 Non-uniqueness, null space… Model “null” space Data space m + m’ d +  F(m’)≈ 0
  • 18.
    11/11/2015 18 david.lumley@uwa.edu.auLumley et al.,2014 Example: low resolution data Gravity data david.lumley@uwa.edu.auLumley et al., 2014 “Mickey Mouse model” Gravity data
  • 19.
    11/11/2015 19 david.lumley@uwa.edu.auLumley et al.,2014 Model “null” space Data space m + imi’ d +  F(m’)≈ 0 * There are infinitely many models that fit the data! david.lumley@uwa.edu.auLumley et al., 2014 Uncertainty ≠ Non-uniqueness
  • 20.
    11/11/2015 20 david.lumley@uwa.edu.auLumley et al.,2014 Inversion …imaging, estimation Model space Data space F-1 m d david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space + uncertainty Data space + errors F-1 +  m +  d + 
  • 21.
    11/11/2015 21 david.lumley@uwa.edu.auLumley et al.,2014 Inversion …imaging, estimation Model space + uncertainty + non-uniqueness Data space + errors F-1 +  m + + m’ d +  david.lumley@uwa.edu.auLumley et al., 2014 Inversion …imaging, estimation Model space + uncertainty + non-uniqueness * Regularization * * Model-shaping * Data space + errors F-1 +  m + + imi’ d + 
  • 22.
    11/11/2015 22 david.lumley@uwa.edu.auLumley et al.,2014 “Mickey Mouse model” Gravity data david.lumley@uwa.edu.auLumley et al., 2014 Outline • Define “4D” • Examples of 4D seismic • Define “uncertainty” • Nonlinear uncertainty analysis + examples
  • 23.
    11/11/2015 23 david.lumley@uwa.edu.auLumley et al.,2014 “Closing the loop… history matching” Observed Data; t++ Inversion Estimated model; t++ Simulation Predicted data david.lumley@uwa.edu.auLumley et al., 2014 4D amplitude difference map extracted along top of reservoir structure Lumley et al., 2003
  • 24.
    11/11/2015 24 david.lumley@uwa.edu.auLumley et al.,2014 Sources of 4D error and uncertainty • 4D Seismic data errors • Non-repeatable noise • Source-receiver positioning errors • Changes in the water column / near-surface / overburden • Changes in acquisition geometry • Changes in source-receiver characteristics • Non 4D-compliant processing flow • Etcetera… david.lumley@uwa.edu.auLumley et al., 2014 3D Noise data = “signal” + noise
  • 25.
    11/11/2015 25 david.lumley@uwa.edu.auLumley et al.,2014 4D NR Noise T1 T2 T2-T1 david.lumley@uwa.edu.auLumley et al., 2014 4D Repeatability Saul & Lumley, 2013
  • 26.
    11/11/2015 26 david.lumley@uwa.edu.auLumley et al.,2014 after Landro 4D NRMS vs. position error david.lumley@uwa.edu.auLumley et al., 2014 image image difference Image difference after 40-60 cm tidal corrections Eiken et al., EAGE 1999 4D tidal corrections
  • 27.
    11/11/2015 27 david.lumley@uwa.edu.auLumley et al.,2014 Line A: before the platform Line B: after the platform with Petrobras david.lumley@uwa.edu.auLumley et al., 2014 “Statistical” image processing Baseline Monitor Difference Lumley et al., SEG, 1998
  • 28.
    11/11/2015 28 david.lumley@uwa.edu.auLumley et al.,2014 Lumley et al., SEG, 1998 Baseline Monitor Difference “Physics-based” image processing david.lumley@uwa.edu.auLumley et al., 2014 1999 Local Diff Global Diff ? 4D Local vs. Global optimization Lumley et al. 2003
  • 29.
    11/11/2015 29 david.lumley@uwa.edu.auLumley et al.,2014 Local image difference Global image difference CO2 injectors? Lumley et al. 2003 4D Local vs. Global Optimization david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Model definition • Model parameterization (acoustic, elastic, aniso, attenuation…) • Physical property relationships (velocity-pressure…) • Model discretization/sampling (fine, coarse, up/down-scale…) • Model relationships (geology, seismic, fluid flow…) • Etcetera…
  • 30.
    11/11/2015 30 david.lumley@uwa.edu.auLumley et al.,2014 Reservoir container david.lumley@uwa.edu.auLumley et al., 2014 Reservoir properties
  • 31.
    11/11/2015 31 david.lumley@uwa.edu.auLumley et al.,2014 Up/down scaling david.lumley@uwa.edu.auLumley et al., 2014 porosity clay fraction
  • 32.
    11/11/2015 32 david.lumley@uwa.edu.auLumley et al.,2014 Rock physics param pdfs david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Physics (modeling/inversion operators/code) • Linear versus nonlinear • Acoustic, Elastic, Anisotropy, Attenuation… • Convolution, Raytracing, Finite Difference… • Algorithm implementations • Etcetera…
  • 33.
    11/11/2015 33 david.lumley@uwa.edu.auLumley et al.,2014 4D FD elastic modeling david.lumley@uwa.edu.auLumley et al., 2014 1 layer CO2 Lumley et al., 2008 synth PSDM
  • 34.
    11/11/2015 34 david.lumley@uwa.edu.auLumley et al.,2014 real PSTM 1 layer CO2 StatoilLumley et al., 2008 synth PSDM david.lumley@uwa.edu.auLumley et al., 2014 Sources of 4D error and uncertainty • Optimization criteria (inversion/estimation) • Least squares (L2), Least absolute (L1), hybrid… • Optimal fit to data, amplitude, phase… • Multiple objectives, weighting schemes… • Inversion constraints (soft, hard, weighted…) • Optimization method (gradients, stochastic, MC, PSO, genetic…) • Resolution, Null space, Non-uniqueness… • Etcetera…
  • 35.
    11/11/2015 35 david.lumley@uwa.edu.auLumley et al.,2014 Multi-objective optimisation find a reservoir model m such that: min E = (seismic)p + (logs)q + (geology)r + … david.lumley@uwa.edu.auLumley et al., 2014 13.22 13.27 13.32 13.37 13.42 13.47 13.52 13.57 36 41 46 ObjectiveFunction2 Objective Function 1 Generation 1 13.22 13.24 13.26 13.28 13.3 13.32 13.34 13.36 35 36 37 38 39 40 ObjectiveFunction2 Objective Function 1 Generation 10 13.12 13.14 13.16 13.18 13.2 13.22 13.24 13.26 30 32 34 36 38 ObjectiveFunction2 Objective Function 1 Generation 20 13 13.02 13.04 13.06 13.08 13.1 13.12 26 27 28 29 30 ObjectiveFunction2 Objective Function 1 Generation 50 12.96 12.97 12.98 12.99 13 13.01 13.02 13.03 13.04 13.05 13.06 24 25 26 27 28 29 ObjectiveFunction2 Objective Function 1 Generation 70 12.95 12.96 12.97 12.98 12.99 13 13.01 13.02 13.03 13.04 13.05 24 25 26 27 28 ObjectiveFunction2 Objective Function 1 Generation 100 Multi-objective optimization – “Pareto front” 70 Niri & Lumley 2013
  • 36.
    11/11/2015 36 david.lumley@uwa.edu.auLumley et al.,2014 a) Reference Litho-facies model b) Before MO model updating c) After MO model updating  Average Mismatch error reduced from 36.5% to 14.6% Multi-objective optimization – “Pareto front” Niri & Lumley 2013 david.lumley@uwa.edu.auLumley et al., 2014 How to quantify 4D errors + uncertainty?
  • 37.
    11/11/2015 37 david.lumley@uwa.edu.auLumley et al.,2014 How to quantify 4D errors + uncertainty? >> Nonlinear stochastic error propagation david.lumley@uwa.edu.auLumley et al., 2014 d1 d2 p N=1000 realizations Sw Pp 4D inversion statistics N=1000
  • 38.
    11/11/2015 38 david.lumley@uwa.edu.auLumley et al.,2014 4D seismic image of water saturation (Sw) a b david.lumley@uwa.edu.auLumley et al., 2014 4D seismic inversion for water saturation (Sw) Sw a b
  • 39.
    11/11/2015 39 david.lumley@uwa.edu.auLumley et al.,2014 {Sw} for 1000 realizations a b david.lumley@uwa.edu.auLumley et al., 2014 signal to noise ratio “S/N” of Sw a b
  • 40.
    11/11/2015 40 david.lumley@uwa.edu.auLumley et al.,2014 Probability that Sw > 0.5 a b david.lumley@uwa.edu.auLumley et al., 2014 “Closing the loop… history matching” Observed Data; t++ Inversion Estimated model; t++ Simulation Predicted data
  • 41.