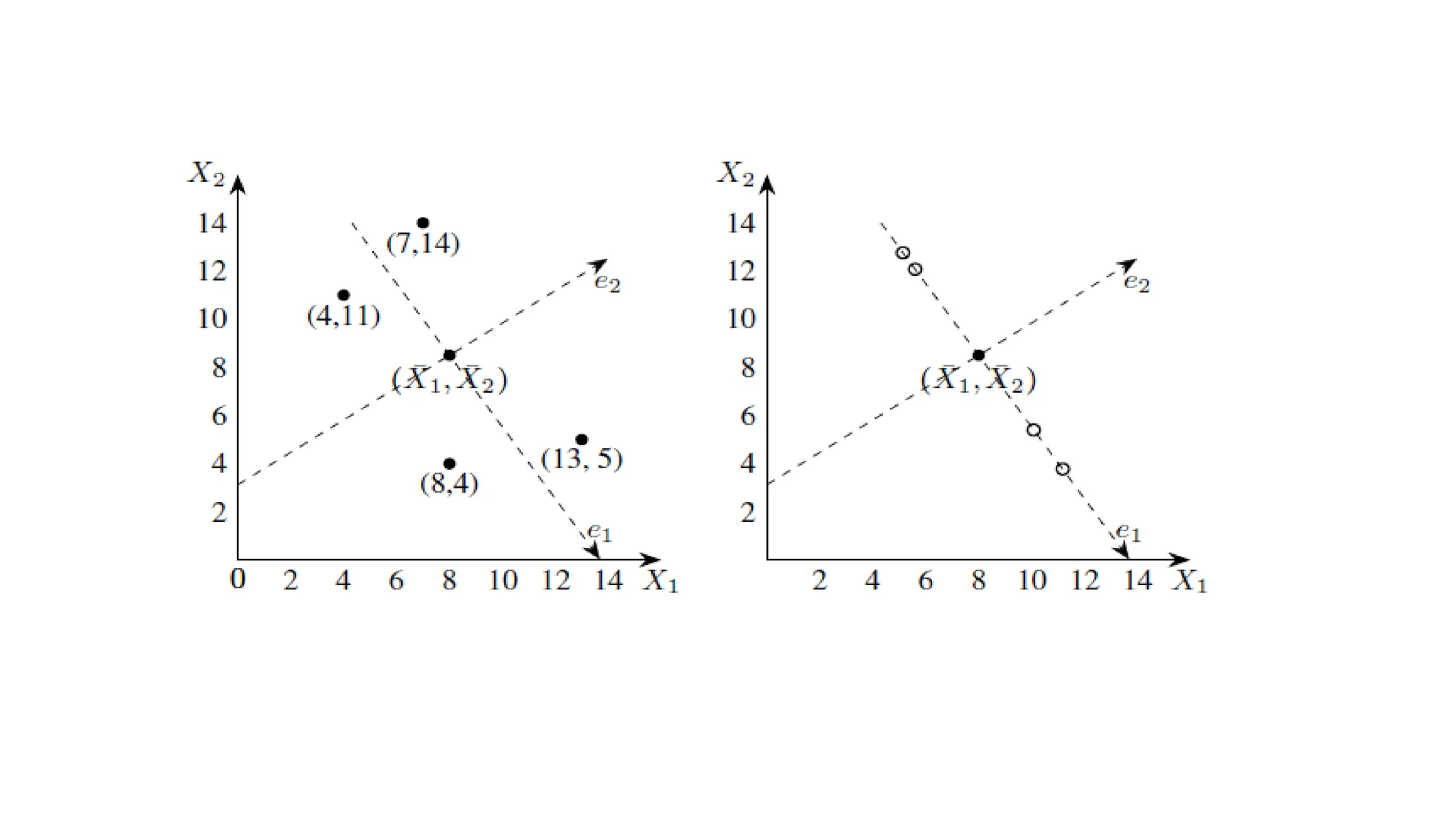
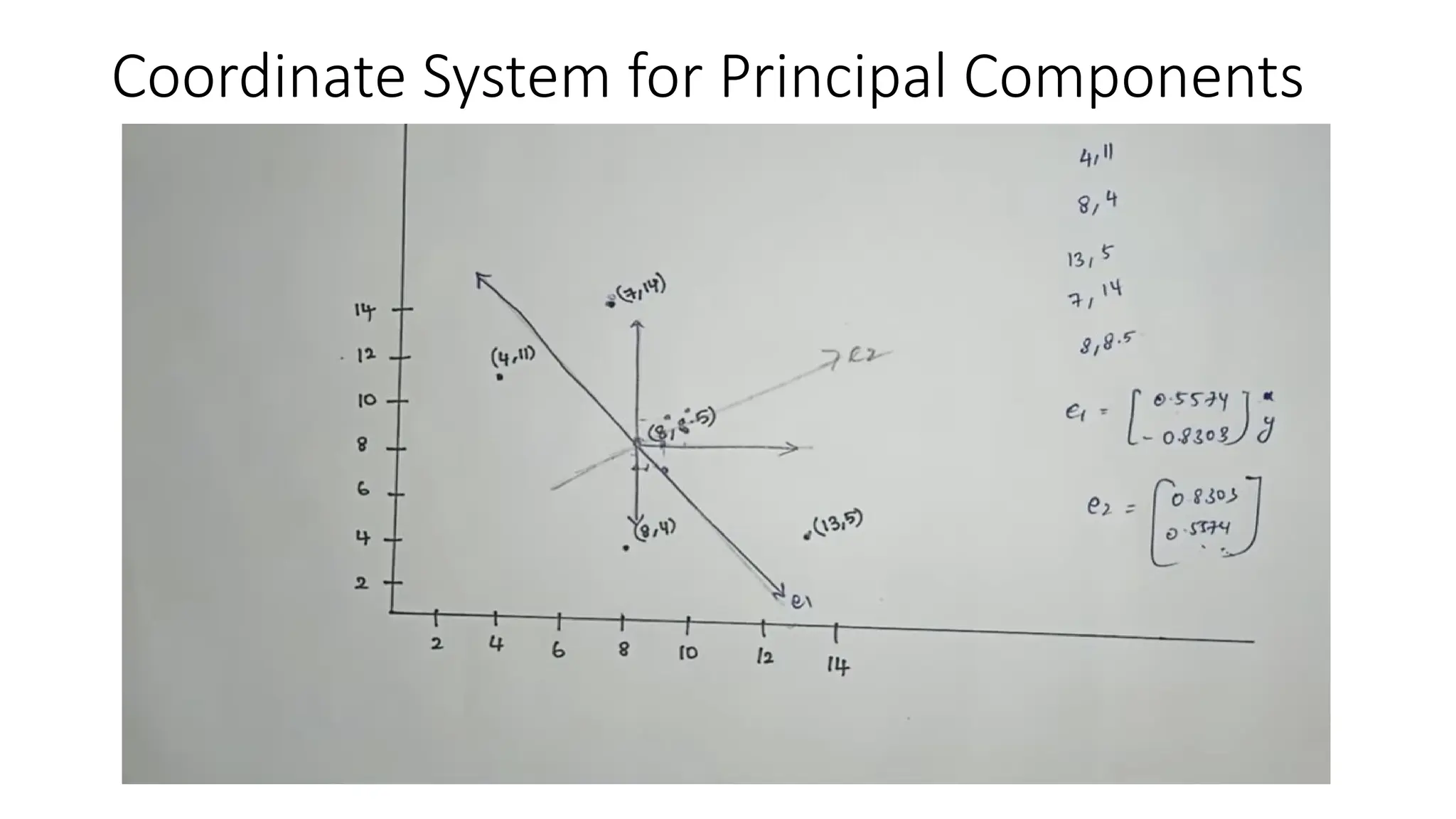
Principal Component Analysis (PCA) is a dimensionality reduction technique that transforms high-dimensional datasets into a new coordinate system, maximizing variance to simplify data while preserving key information. It uses the covariance matrix to identify relationships between features and employs eigenvalues and eigenvectors to determine directions of maximum variance. PCA helps mitigate issues related to high-dimensional data, such as overfitting and visualization challenges, by filtering out noise and focusing on significant features.

1. Principal Component Analysis
• Principal Component Analysis (PCA) is a dimensionality reduction
technique widely used in machine learning and statistics. Its primary
goal is to transform a dataset into a new coordinate system in such a
way that the greatest variance lies along the first axis, the second
greatest variance along the second axis, and so on. This helps to
reduce the dimensionality of the data while retaining as much of its
variability as possible.
• Principal component analysis (PCA) is a statistical procedure that uses
an orthogonal transformation to convert a set of observations of
possibly correlated variables into a set of values of linearly
uncorrelated variables called principal components.

2. Need of Principal Component Analysis
1. Dimensionality Reduction
Problem: High-dimensional datasets may suffer from the curse of dimensionality, leading to
increased computational complexity, overfitting, and difficulty in visualization.
Solution: PCA reduces the number of dimensions while retaining as much variability as possible,
helping to simplify the dataset without losing critical information.
2. Visualization
Problem: Visualizing high-dimensional data is challenging, and it is often beneficial to reduce the
data to two or three dimensions for easier interpretation.
Solution: PCA projects data onto a lower-dimensional space, allowing for visualization in 2D or 3D
while preserving the major trends and patterns in the data.
3. Noise Reduction
Problem: Datasets may contain noise or irrelevant features that can obscure meaningful patterns.
Solution: By focusing on the principal components associated with the highest variance, PCA
helps to filter out noise and highlight the most significant features.

3. Covariance Matrix
• The covariance matrix is crucial in PCA for dimensionality reduction and feature
extraction.
• PCA aims to transform data into a new set of uncorrelated variables, called
principal components, ordered by their variance.
• The covariance matrix captures the relationships between original features,
guiding PCA to find the directions of maximum variance.
• Consider a dataset with features like height and weight; the covariance matrix
reveals how changes in one variable relate to changes in the other. High
covariance suggests a strong relationship, while low covariance indicates
independence.
• PCA leverages this information to identify principal components, allowing for
dimensionality reduction while retaining key information, as exemplified in
transforming height and weight data into uncorrelated principal components.

4. Eigen Vectors and Eigen values
• In PCA, the covariance matrix represents the relationships and variability among features.
• Eigenvectors of the covariance matrix indicate the directions of maximum variance, while
eigenvalues quantify the magnitude of variance along those directions.
• When applying PCA to a dataset, the eigenvalues represent the amount of information
each principal component retains.
• For example, consider a covariance matrix representing the heights and weights of
individuals; the eigenvectors would show the directions in this two-dimensional space
with the most variance, like a principal axis of height and weight. The corresponding
eigenvalues would reveal how much variance is captured along each principal axis,
guiding the selection of the most informative components for dimensionality reduction.

5. Principal Components
Principal components in PCA are the new orthogonal variables formed
as linear combinations of the original features.
They capture the maximum variance in the data, with the first principal
component explaining the most variance, followed by subsequent
components. The use of principal components lies in dimensionality
reduction, allowing representation of the dataset in a lower-
dimensional space while retaining essential information.

6. Step-by-step explanation of the PCA
1.Standardize the Data by calculating the mean
2.Computes the covariance matrix.
3. Calculate Eigen values
0=determinant(S- I)
ℷ
Where S is covariance matrix and I is identity matrix

7. Step 4: Calculate eigenvectors for the covariance matrix.
(S-ℷI)U=0, where U= u1
u2
Step 5: Calculate unit eigenvector.
e1= u1
|u1|
Step 6: Transform the original matrix, by calculating all principal
component analysis
After that, we project the data along the eigen vectors. If the original data
has a dimensionality of n, we can reduce dimensions to k, such that k≤ n.

9. Example

20. Coordinate System for Principal Components