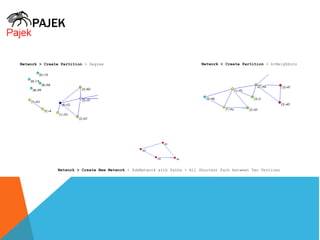
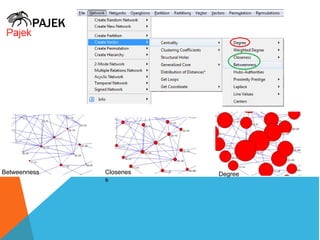
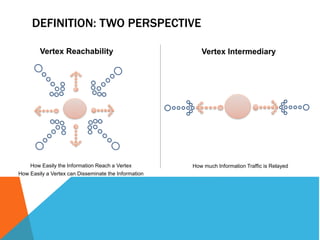
This document discusses different measures of centrality in networks: degree centrality, closeness centrality, and betweenness centrality. Degree centrality is a measure of how connected a node is based on its number of connections. Closeness centrality quantifies how close a node is to all other nodes based on the shortest path distances. Betweenness centrality measures the number of shortest paths that pass through a node, indicating its importance as an intermediary. The document also describes how to calculate centralization measures for networks based on these centrality metrics.

2. NETWORK AS A MEDIA
• Transmission  Flow
• Information
• Goods
• Service
• Network Analysis is to STUDY
• Critical Actors  Vertex Centrality
• Critical Path
• Diffusion Rate  Network Centralization

3. VERTEX CENTRALITY
HM-1: Articular the Diffusion through all Regions
HP -6: In Case of Malfunction  Not a Disaster

4. NETWORK CENTRALIZATION
Looks Counterintuitive
The More Number of Central
Vertex Cause Less Compact
Network
Vertex Centrality DEFINES
Network Centralization
1 Most, 4 Least Central 3 Most, 2 Least Central
The More VARIATION in Vertices Centrality  Higher Network Centralization

5. DEFINITION: TWO PERSPECTIVE
Vertex Reachability Vertex Intermediary
How Easily the Information Reach a Vertex
How Easily a Vertex can Disseminate the Information
How much Information Traffic is Relayed

6. DEGREE CENTRALITY: UNDIRECTED NET
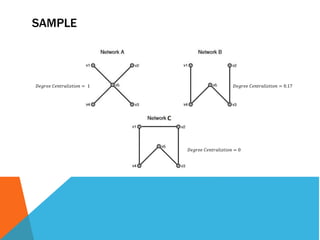
• Degree Centrality of a Vertex
 Vertex Degree
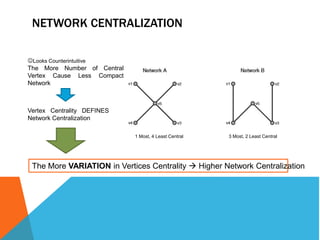
• Degree Centralization of a Network
푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 푣 [푀푎푥 퐷푒푔푟푒푒 − deg(푣)]
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 퐻푎푝푝푒푛푠 푖푛 푆푡푎푟 − 푁푒푡푤표푟푘 푖푛 푈푛푑푖푟푒푐푡푒푑 푆푖푚푝푙푒 푁푒푡푤푟표푘
퐶푒푛푡푟푎푙푖푧푎푡푖표푛 푉푎푙푢푒 =
푉푎푟푖푎푡푖표푛 푉푎푙푢푒
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒=(푛−1)×(푛−2)
푛: 푉푒푟푡푖푐푒푠 퐶표푢푛푡
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 3 ∗ 3 − 1 + 1 ∗ 3 − 3 = 6 푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 12 푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 20
For Directed Network this Definition will not Work!

7. SAMPLE
퐷푒푔푟푒푒 퐶푒푛푡푟푎푙푖푧푡푖표푛 = 1 퐷푒푔푟푒푒 퐶푒푛푡푟푎푙푖푧푡푖표푛 = 0.17
퐷푒푔푟푒푒 퐶푒푛푡푟푎푙푖푧푡푖표푛 = 0

8. CLOSENESS CENTRALITY
• Degree Centrality has Local View of Vertex Neighborhood
• Global View
• Distance to all Other Vertices: The Closer Path  The Faster Diffusion
• Geodesic  Shortest Path Between Two Vertices
• Distance Length of Geodesic Path
• Closeness Centrality of a Vertex
퐶푣 =
푛 −1
푢≠푣 퐷푖푠푡푎푛푐푒(푢,푣)
• Closeness Centralization of a Network
푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 푣 [푀푎푥 퐶푒푛푡푟푎푙푖푡푦 − 퐶푣 ]
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 퐻푎푝푝푒푛푠 푖푛 푆푡푎푟 − 푁푒푡푤표푟푘 푖푛 푈푛푑푖푟푒푐푡푒푑 푆푖푚푝푙푒 푁푒푡푤푟표푘
푉푎푟푖푎푡푖표푛 푉푎푙푢푒
퐶푒푛푡푟푎푙푖푧푎푡푖표푛 푉푎푙푢푒 =
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒=2 × 푛−1 ×(푛−2)
푀푎푥 퐶푣 = 1 푖푛 푆푡푎푟 − 푁푒푡푤표푟푘
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 = 푛 − 1 × 1 + 2 × 푛 − 2 − 1 = 24

9. BETWEENNESS CENTRALITY
• Intermarry Vertex, Relaying Node
How Many Flows of Information are Disrupted or Must Make Longer Detours if
a Vertex Stops Passing on Information!
 Betweenness Centrality of a Vertex
The Proportion of all Geodesics Between Pairs of Other Vertices that Include
This Vertex
 Betweenness Centralization
 푉푎푟푖푎푡푖표푛 푖푛 푡ℎ푒 퐵푒푡푤푒푒푛푛푒푠푠 퐶푒푛푡푟푎푙푖푡푦 표푓 푉푒푟푡푖푐푒푠
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 표푓 퐵푒푡푤푒푒푛푛푒푠 퐶푒푛푡푟푎푙푖푡푦
Degree Centralization =
푉푎푟푖푎푡푖표푛 푖푛 푡ℎ푒 퐷푒푔푟푒푒 퐶푒푛푡푟푎푙푖푡푦 표푓 푉푒푟푡푖푐푒푠
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 표푓 퐷푒푔푟푒푒 퐶푒푛푟푎푙푖푡푦
Closeness Centralization =
푉푎푟푖푎푡푖표푛 푖푛 푡ℎ푒 퐶푙표푠푒푛푒푠푠 퐶푒푛푡푟푎푙푖푡푦 표푓 푉푒푟푡푖푐푒푠
푀푎푥 푉푎푟푖푎푡푖표푛 푉푎푙푢푒 표푓 퐶푙표푠푒푛푒푠푠 퐶푒푛푡푟푎푙푖푡푦

10. PAJEK
Network > Create Partition > Degree Network > Create Partition > k-Neighbors
Network > Create New Network > SubNetwork with Paths > All Shortest Path between Two Vertices

11. PAJEK
Closenes Degree
s
Betweenness